Using Hybrid CPU-GPU Platforms to Accelerate the Computation of the Matrix Sign Function
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Unicode Request for Cyrillic Modifier Letters Superscript Modifiers
Unicode request for Cyrillic modifier letters L2/21-107 Kirk Miller, [email protected] 2021 June 07 This is a request for spacing superscript and subscript Cyrillic characters. It has been favorably reviewed by Sebastian Kempgen (University of Bamberg) and others at the Commission for Computer Supported Processing of Medieval Slavonic Manuscripts and Early Printed Books. Cyrillic-based phonetic transcription uses superscript modifier letters in a manner analogous to the IPA. This convention is widespread, found in both academic publication and standard dictionaries. Transcription of pronunciations into Cyrillic is the norm for monolingual dictionaries, and Cyrillic rather than IPA is often found in linguistic descriptions as well, as seen in the illustrations below for Slavic dialectology, Yugur (Yellow Uyghur) and Evenki. The Great Russian Encyclopedia states that Cyrillic notation is more common in Russian studies than is IPA (‘Transkripcija’, Bol’šaja rossijskaja ènciplopedija, Russian Ministry of Culture, 2005–2019). Unicode currently encodes only three modifier Cyrillic letters: U+A69C ⟨ꚜ⟩ and U+A69D ⟨ꚝ⟩, intended for descriptions of Baltic languages in Latin script but ubiquitous for Slavic languages in Cyrillic script, and U+1D78 ⟨ᵸ⟩, used for nasalized vowels, for example in descriptions of Chechen. The requested spacing modifier letters cannot be substituted by the encoded combining diacritics because (a) some authors contrast them, and (b) they themselves need to be able to take combining diacritics, including diacritics that go under the modifier letter, as in ⟨ᶟ̭̈⟩BA . (See next section and e.g. Figure 18. ) In addition, some linguists make a distinction between spacing superscript letters, used for phonetic detail as in the IPA tradition, and spacing subscript letters, used to denote phonological concepts such as archiphonemes. -

The Cyrillic Manuscript Codices of Budapest University Library
polata k)¢∞igopis|¢aq kz— - ki—, 1995: 5–12 THE CYRILLIC MANUSCRIPT CODICES OF BUDAPEST UNIVERSITY LIBRARY Ralph M. Cleminson The Library of the University of Budapest (Eötvös Loránd Tudomány- egyetem Könyvtára) possesses nine mediæval cyrillic manuscript codices, numbered Codd. slav. 1, 3-5, 7b, 7c, 9-11. (Cod. slav. 2 is Polish, Cod. slav. 6 is Czech, Cod. slav. 7a is the former shelfmark of the present Cod. slav. 10, and there is no Cod. slav. 8.) Codd. slav 1-5 were described (very badly) in A Budapesti M. Kir. Egyetemi Könyvtár codexeinek czímjegyzéke, Budapest, 1881, pp.100-101, and three of them (Codd. slav. 1, 7c, 9) have so far been noted in the inventory of Slavonic manuscripts in Hungary which is currently being produced (Magyarországi szláv kéziratok, (Foªszerkesztoª Nyomárkay I.), I-, Budapest, 1990-). Apart from this the manuscripts seem to have been largely neglected. The present descriptions, made during a visit to the Library in December 1991, have the object of acquainting the scholarly community with the Library’s holdings. They follow the format and practice described on pp.ix-x of my Union Catalogue of Cyrillic Manuscripts in British and Irish Collections (London, 1988). Cod. slav. 1 APOSTOL, Serbian, 1572 i + 211 leaves, foliated [i], 1-211. Collation: I8-XXVI8, 3 leaves (=XXVII). Gatherings signed front and back a–-kz–. Paper: w/m (i) an anchor, (ii) a coat of arms, both too faint to permit precise identification. Size of leaves: 305mm x 210mm. Ink: brownish-black; red, and occasionally yellow, for titles, initials and rubrics. -

Descriptions and Records of Bees - LVI
Utah State University DigitalCommons@USU Co Bee Lab 1-1-1914 Descriptions and Records of Bees - LVI T. D. A. Cockerell University of Colorado Follow this and additional works at: https://digitalcommons.usu.edu/bee_lab_co Part of the Entomology Commons Recommended Citation Cockerell, T. D. A., "Descriptions and Records of Bees - LVI" (1914). Co. Paper 518. https://digitalcommons.usu.edu/bee_lab_co/518 This Article is brought to you for free and open access by the Bee Lab at DigitalCommons@USU. It has been accepted for inclusion in Co by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. F,·0111tlte .\..N'.\'AT,S AN!) "J.A.OA7.['.\'is OF' ~ATIJHA.r. ITr s TOltY :::iel'8, \ 'ol. xiii. , .Tw11wry lUl.J.. ' r Descriptions and Recoi·ds of Bees.-LVI. 1 By 1 • D. A. CucKERELL, University of Colorado. Stenotritus elegans, Smith, variety a. A female from Tennant's Creek, Central Australia (Field; Nat. Mus . Victoria, 46), Las apparent ly been in alcohol, autl the pubescence is in bad condition. So far as can be made out, there i no fuscous hair on the thorax above, alld no black Ii air on the abdomen. The mesothorax shows olive green tints in front. 1'1.ie first r. n. joins the secoml s.m. a little before the middle, in stead of a little beyoucl a. in Smith's type of S. eLegans. Possib ly this is a distinct species, but it cannot be satisfacto rily separated without better material. No ruales a signed to Stenotritus are known; but it seems 1:37 Mr. -

Aviso De Conciliación De Demanda Colectiva Sobre Los Derechos De Los Jóvenes Involucrados En El Programa Youth Accountability Team (“Yat”) Del Condado De Riverside
AVISO DE CONCILIACIÓN DE DEMANDA COLECTIVA SOBRE LOS DERECHOS DE LOS JÓVENES INVOLUCRADOS EN EL PROGRAMA YOUTH ACCOUNTABILITY TEAM (“YAT”) DEL CONDADO DE RIVERSIDE Este aviso es sobre una conciliación de una demanda colectiva contra el condado de Riverside, la cual involucra supuestas violaciones de los derechos de los jóvenes que han participado en el programa Youth Accountability Team (“YAT”) dirigido por la Oficina de Libertad condicional del Condado de Riverside. Si alguna vez se lo derivó al programa YAT, esta conciliación podría afectar sus derechos. SOBRE LA DEMANDA El 1 de julio de 2018, tres jóvenes del condado de Riverside y una organización de tutelaje de jóvenes presentaron esta demanda colectiva, de nombre Sigma Beta Xi, Inc. v. County of Riverside. La demanda cuestiona la constitucionalidad del programa Youth Accountability Team (“YAT”), un programa de recuperación juvenil dirigido por el condado de Riverside (el “Condado”). La demanda levantó una gran cantidad de dudas sobre las duras sanciones impuestas sobre los menores acusados solo de mala conducta escolar menor. La demanda alegaba que el programa YAT había puesto a miles de menores en contratos onerosos de libertad condicional YAT en base al comportamiento común de los adolescentes, incluida la “persistente o habitual negación a obedecer las órdenes o las instrucciones razonables de las autoridades escolares” en virtud de la sección 601(b) del Código de Bienestar e Instituciones de California (California Welfare & Institutions Code). La demanda además alegaba que el programa YAT violaba los derechos al debido proceso de los menores al no notificarles de forma adecuada sobre sus derechos y al no proporcionarles orientación. -

Rab P Yat Bbit Proje Es C and Ect R Coun Cav Reco Nty 4- Vy Sc Rd B -H Cienc Ook Ce
Year: _________ Yates County 4-H Rabbit and Cavy Science Project Record Book Place picture of project animal(s) here. Name: ______________________________ Age (as of Jan 1): ____________ Club: _______________________________ Number of Years in 4-H: _______ Number of Years in project work: ________ (rabbit) ________ (cavy) My goals for this year are: ___________________________________________________ ___________________________________________________ ___________________________________________________ ___________________________________________________ ___________________________________________________ ___________________________________________________ ___________________________________________________ 1 HELPFUL HINTS: Keep your receipts; it will make it easier to fill out the Expense Record! You may want to create a folder or a special drawer to keep them in! Hang the Labor Record by your animal’s feed or somewhere you go each day and will see it. If you did not do any work in a specific section for the year, just write “not applicable” at the top of the page and skip to the next section. You will not be penalized. Estimates are ok! If you need additional pages, feel free to attach them to the back. If you have a question, ask someone… you can always call the 4-H office at 315-536-5123. Project records are due with your fair pre-entry form. These are not made to be hard or intimidating; just to show you how much time, effort and care you and/or your family really put into your project animal in a year. We don’t expect that you are the sole care-giver for your animal. Therefore, we understand if you leave spaces blank. Just don’t lie. Be honest - if you didn’t take care of your animal for a few days or if someone picked up the food one week and didn’t tell you how much it cost, it is ok. -

Language Specific Peculiarities Document for Halh Mongolian As Spoken in MONGOLIA
Language Specific Peculiarities Document for Halh Mongolian as Spoken in MONGOLIA Halh Mongolian, also known as Khalkha (or Xalxa) Mongolian, is a Mongolic language spoken in Mongolia. It has approximately 3 million speakers. 1. Special handling of dialects There are several Mongolic languages or dialects which are mutually intelligible. These include Chakhar and Ordos Mongol, both spoken in the Inner Mongolia region of China. Their status as separate languages is a matter of dispute (Rybatzki 2003). Halh Mongolian is the only Mongolian dialect spoken by the ethnic Mongolian majority in Mongolia. Mongolian speakers from outside Mongolia were not included in this data collection; only Halh Mongolian was collected. 2. Deviation from native-speaker principle No deviation, only native speakers of Halh Mongolian in Mongolia were collected. 3. Special handling of spelling None. 4. Description of character set used for orthographic transcription Mongolian has historically been written in a large variety of scripts. A Latin alphabet was introduced in 1941, but is no longer current (Grenoble, 2003). Today, the classic Mongolian script is still used in Inner Mongolia, but the official standard spelling of Halh Mongolian uses Mongolian Cyrillic. This is also the script used for all educational purposes in Mongolia, and therefore the script which was used for this project. It consists of the standard Cyrillic range (Ux0410-Ux044F, Ux0401, and Ux0451) plus two extra characters, Ux04E8/Ux04E9 and Ux04AE/Ux04AF (see also the table in Section 5.1). 5. Description of Romanization scheme The table in Section 5.1 shows Appen's Mongolian Romanization scheme, which is fully reversible. -

CONGRESSION.. ~Li RECORD-· HOU&E
I CONGRESSION.._~li RECORD-· HOU&E. JUNE 18, . The Secretary called the· roll, ::tnd the following Senators an- The Post Office Department'a expectation of saving $7,000 000, re ferred to by Representative· S.TEENERSON, is.. fully justified. as will. be swered to tlieir nam-e.s.:- · · seen from the following reports on authorized annual rate of pay to the Beckham Harding Lewlcr Sheppard railroads at various dates..: Borah Hardwick McLean Sherman o'ct. 31, 1916, on weight basis:_____ :.._ '------------- $G2, 242, 000 I Bra.ndeg~e Henderson· Jl.lcNary Smi~.MiL Nov. 1, 1916, weight and spaec combined--------------- 65, 4!:>2, 000 Calder Hollis _ Norris Smith, S. C. July 1, 1917, weight and space combined__________ 58,518-, 000 I Chamberlain J ob.nson;Cal. Nugent' Smoot Sept. 30, 1917, weight and space. combine<L ____ ._______ 56, 509, 000 Colt Johnson, S. Dak. Page Tillma-n Dec... 31, 1917, weight and space combined_________ 55, 040, 000 CumminS' Jone~; Wa.sh. Phelan.. · Townsend Mar; 31, 1918, weight and space combined_____________ 53, 8{)0, 000 Curtis Kenyon Poindext~ TraminelL Dillingham King Ransdell Vardaman U there is still doubt in the mind o1 anyone as to whethet• the Post Gerry Kirby. Robinson Wadsworth Office Department has reduc£(} the cost of carrying: the mails on railway Guion Knox Saulsbury Watson lines, let him ask the-railroads. Hale I..enroot Shafroth Sincerely, yours, A. S. BURLESON, Postmaster Gcne1·al . llli·. SHAFROTH.. I desire to announce tlie absence: oi my colleague [Mr. THOMAS] on official business; [From the CoxanES.s:IOXAL. -

1 Symbols (2286)
1 Symbols (2286) USV Symbol Macro(s) Description 0009 \textHT <control> 000A \textLF <control> 000D \textCR <control> 0022 ” \textquotedbl QUOTATION MARK 0023 # \texthash NUMBER SIGN \textnumbersign 0024 $ \textdollar DOLLAR SIGN 0025 % \textpercent PERCENT SIGN 0026 & \textampersand AMPERSAND 0027 ’ \textquotesingle APOSTROPHE 0028 ( \textparenleft LEFT PARENTHESIS 0029 ) \textparenright RIGHT PARENTHESIS 002A * \textasteriskcentered ASTERISK 002B + \textMVPlus PLUS SIGN 002C , \textMVComma COMMA 002D - \textMVMinus HYPHEN-MINUS 002E . \textMVPeriod FULL STOP 002F / \textMVDivision SOLIDUS 0030 0 \textMVZero DIGIT ZERO 0031 1 \textMVOne DIGIT ONE 0032 2 \textMVTwo DIGIT TWO 0033 3 \textMVThree DIGIT THREE 0034 4 \textMVFour DIGIT FOUR 0035 5 \textMVFive DIGIT FIVE 0036 6 \textMVSix DIGIT SIX 0037 7 \textMVSeven DIGIT SEVEN 0038 8 \textMVEight DIGIT EIGHT 0039 9 \textMVNine DIGIT NINE 003C < \textless LESS-THAN SIGN 003D = \textequals EQUALS SIGN 003E > \textgreater GREATER-THAN SIGN 0040 @ \textMVAt COMMERCIAL AT 005C \ \textbackslash REVERSE SOLIDUS 005E ^ \textasciicircum CIRCUMFLEX ACCENT 005F _ \textunderscore LOW LINE 0060 ‘ \textasciigrave GRAVE ACCENT 0067 g \textg LATIN SMALL LETTER G 007B { \textbraceleft LEFT CURLY BRACKET 007C | \textbar VERTICAL LINE 007D } \textbraceright RIGHT CURLY BRACKET 007E ~ \textasciitilde TILDE 00A0 \nobreakspace NO-BREAK SPACE 00A1 ¡ \textexclamdown INVERTED EXCLAMATION MARK 00A2 ¢ \textcent CENT SIGN 00A3 £ \textsterling POUND SIGN 00A4 ¤ \textcurrency CURRENCY SIGN 00A5 ¥ \textyen YEN SIGN 00A6 -

TLD: Сайт Script Identifier: Cyrillic Script Description: Cyrillic Unicode (Basic, Extended-A and Extended-B) Version: 1.0 Effective Date: 02 April 2012
TLD: сайт Script Identifier: Cyrillic Script Description: Cyrillic Unicode (Basic, Extended-A and Extended-B) Version: 1.0 Effective Date: 02 April 2012 Registry: сайт Registry Contact: Iliya Bazlyankov <[email protected]> Tel: +359 8 9999 1690 Website: http://www.corenic.org This document presents a character table used by сайт Registry for IDN registrations in Cyrillic script. The policy disallows IDN variants, but prevents registration of names with potentially similar characters to avoid any user confusion. U+002D;U+002D # HYPHEN-MINUS -;- U+0030;U+0030 # DIGIT ZERO 0;0 U+0031;U+0031 # DIGIT ONE 1;1 U+0032;U+0032 # DIGIT TWO 2;2 U+0033;U+0033 # DIGIT THREE 3;3 U+0034;U+0034 # DIGIT FOUR 4;4 U+0035;U+0035 # DIGIT FIVE 5;5 U+0036;U+0036 # DIGIT SIX 6;6 U+0037;U+0037 # DIGIT SEVEN 7;7 U+0038;U+0038 # DIGIT EIGHT 8;8 U+0039;U+0039 # DIGIT NINE 9;9 U+0430;U+0430 # CYRILLIC SMALL LETTER A а;а U+0431;U+0431 # CYRILLIC SMALL LETTER BE б;б U+0432;U+0432 # CYRILLIC SMALL LETTER VE в;в U+0433;U+0433 # CYRILLIC SMALL LETTER GHE г;г U+0434;U+0434 # CYRILLIC SMALL LETTER DE д;д U+0435;U+0435 # CYRILLIC SMALL LETTER IE е;е U+0436;U+0436 # CYRILLIC SMALL LETTER ZHE ж;ж U+0437;U+0437 # CYRILLIC SMALL LETTER ZE з;з U+0438;U+0438 # CYRILLIC SMALL LETTER I и;и U+0439;U+0439 # CYRILLIC SMALL LETTER SHORT I й;й U+043A;U+043A # CYRILLIC SMALL LETTER KA к;к U+043B;U+043B # CYRILLIC SMALL LETTER EL л;л U+043C;U+043C # CYRILLIC SMALL LETTER EM м;м U+043D;U+043D # CYRILLIC SMALL LETTER EN н;н U+043E;U+043E # CYRILLIC SMALL LETTER O о;о U+043F;U+043F -
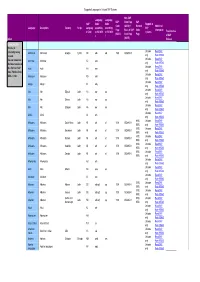
Supported Languages in Unicode SAP Systems Index Language
Supported Languages in Unicode SAP Systems Non-SAP Language Language SAP Code Page SAP SAP Code Code Support in Code (ASCII) = Blended Additional Language Description Country Script Languag according according SAP Page Basis of SAP Code Information e Code to ISO 639- to ISO 639- systems Translated as (ASCII) Code Page Page 2 1 of SAP Index (ASCII) Release Download Info: AThis list is Unicode Read SAP constantly being Abkhazian Abkhazian Georgia Cyrillic AB abk ab 1500 ISO8859-5 revised. only Note 895560 Unicode Read SAP You can download Achinese Achinese AC ace the latest version of only Note 895560 Unicode Read SAP this file from SAP Acoli Acoli AH ach Note 73606 or from only Note 895560 Unicode Read SAP SDN -> /i18n Adangme Adangme AD ada only Note 895560 Unicode Read SAP Adygei Adygei A1 ady only Note 895560 Unicode Read SAP Afar Afar Djibouti Latin AA aar aa only Note 895560 Unicode Read SAP Afar Afar Eritrea Latin AA aar aa only Note 895560 Unicode Read SAP Afar Afar Ethiopia Latin AA aar aa only Note 895560 Unicode Read SAP Afrihili Afrihili AI afh only Note 895560 6100, Unicode Read SAP Afrikaans Afrikaans South Africa Latin AF afr af 1100 ISO8859-1 6500, only Note 895560 6100, Unicode Read SAP Afrikaans Afrikaans Botswana Latin AF afr af 1100 ISO8859-1 6500, only Note 895560 6100, Unicode Read SAP Afrikaans Afrikaans Malawi Latin AF afr af 1100 ISO8859-1 6500, only Note 895560 6100, Unicode Read SAP Afrikaans Afrikaans Namibia Latin AF afr af 1100 ISO8859-1 6500, only Note 895560 6100, Unicode Read SAP Afrikaans Afrikaans Zambia -

Compounding Forms of Inequality: Cape Verdean Migrants' Struggles
MOUTON EuJAL 2020; 8(2): 307–332 Bernardino Tavares* Compounding forms of inequality: Cape Verdean migrants’ struggles in education and beyond in Luxembourg https://doi.org/10.1515/eujal-2020-0007 Abstract: This paper seeks to show how language, combined with other social variables, exacerbates migrants’ and their descendants’ struggles at school and beyond in Luxembourg. To a certain extent, the official trilingualism of Luxem- bourg – French, German and Luxembourgish – corresponds to an ‘elite multilin- gualism’ (Garrido 2017; Barakos and Selleck 2018) which defines who can access certain resources, e. g. education, work etc., and who can be left playing catch-up. The latter are those migrants who I here conceive as multilinguals on the margins. The elitist system is a form of domination and power over those whose language repertoire is less valued. Migrants’ disadvantage is further impacted by other in- dicators of their identity that can go beyond their educational qualifications and language repertoire per se, such as their country of origin, ethnicity, race, gender, citizenship etc. Language intersects with other forms of disadvantage or privi- leges. From an ethnographic sociolinguistic perspective, drawing on interviews and participant observations, this paper will illustrate this intersection of lan- guage, race and ethnicity, and struggles from the ground-level educational reali- ties and aspirations of Cape Verdean migrants and their descendants in Luxem- bourg. This helps cast light on the social organisation in Luxembourg and under- stand the effects of multilingualism in creating ‘abyssal lines’ (Santos 2007) between the nationals, certain European migrants, Lusophone and African mi- grants in terms of social and economic mobility. -

Cómo Entender Y Vivir Con Glaucoma
C óm o E n t e n d e r y V i v i r C o n G l a u c o m a Carlota del Portillo tiene la esperanza de que las futuras generaciones no tengan que vivir con glaucoma. Gracias a los avances en la investigación del Dr. Calkins, es posible que así sea. Glaucoma Research Foundation Allergan proporciona un subsidio educativo ilimitado para la producción de este folleto. “Mi deseo para el futuro es que nadie tenga que vivir con el miedo de perder la vista”. Carlota del Portillo Carlota del Portillo Carlota del Portillo, decano en el Mission Campus de City College of San Francisco, ha sido activista en la comunidad latina desde 1970, además de trabajar en posiciones de liderazgo con el gobierno de la ciudad de San Francisco. Cómo Entender y Vivir Con Glaucoma Índice Comprender qué es el glaucoma 2 ¿Qué es el glaucoma? 3 Cuál es la función del ojo 5 El ojo con glaucoma 5 ¿Se presentan síntomas? 6 ¿Qué puede hacer para prevenir la pérdida de la vista? 7 Diferentes tipos de glaucoma Detectar el glaucoma 10 ¿Cómo se diagnostica el glaucoma? 10 Qué esperar durante los exámenes del glaucoma Tratamiento del glaucoma 14 ¿Existe una cura? 14 Medicamentos para el glaucoma 17 Cirugía de glaucoma Vivir con glaucoma 20 Colaborar con su médico 21 ¿Qué puede hacer para controlar el glaucoma? 23 Sus sentimientos son importantes 24 No permita que el glaucoma limite su vida 25 Gotas oftálmicas Apéndice 27 Glosario 29 Guía de los medicamentos para el glaucoma 1 Comprender qué es el glaucoma ¿Quién puede tener glaucoma? Cualquier persona.