Institute of Physics Nuclear Spin Measurements in Some Nuclides of the Alkali Elements Rubidium and Francium
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Laser Spectroscopy of Neutron Rich Bismuth Isotopes
CERN LIBRARIES, GENEVA new lllllllllllIllllllllllllllllllllllllllllllll SC00000267 CD [L] Q D K,Q/pm lO CERN/ISC 94-7 P60 scP GEM} »- emit 1=·1>.o1=·osAL TO THE rsotos COMMITTEE 9 Le-? Laser Spectroscopy of Neutron Rich Bismuth Isotopes CERN1 — Mainz? — Manchester3 — Stony Brook4 Collaboration J. Behr4, J. Billowes3, P. Campbell3, T.G. Cooperg, U. Georg2, I.S. Grant3, G. Gwinner4, G. Huber], M. Keimz, J. Kilgallon3, A. Kleinz, R. Neugart2, M. Neurothz, G.D. Sprouse‘*, P.D. Wheelera, F. Xu‘* and the ISOLDE Collaboration] Spokesman: J. Billowes Contactman: G. Huber Summary The aim of the proposed experiment is to measure the optical isotope shifts and hyperfine structures of bismuth isotopes in the region 21°'2“Bi which lie above the N=126 shell closure. The change in nuclear mean square charge radii and static moments can be deduced. These will be the first isotones of lead to be measured immediately above the shell closure. This will provide new information on the systematics of the kink in the charge radii change with neutron number seen in the Pb isotopic chain, and will represent the first measurement of the odd proton hg/2 moment in the region above the closed 2°8Pb core. Laser resonance fluorescence will be used on the isotopic bismuth samples as they are released into a gas cell trap. This is a method that has been applied very successfully at SUNY, Stony Brook to the neutron deficient bismuth isotopes and it makes efficient use of the small samples available. The bismuth samples of 212Bi and 213Bi will be prepared by catching intense beams of 22°Fr and 2"Fr on thin lead foils. -

WO 2014/138594 Al 12 September 2014 (12.09.2014) P O P C T
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2014/138594 Al 12 September 2014 (12.09.2014) P O P C T (51) International Patent Classification: ue, Unit 1, Somerville, Massachusetts 02143 (US). PA- C12P 7/52 (2006.01) POULIS, Andrew; 186 Turnpike Street, Canton, Mas sachusetts 02021 (US). KORYABKINA, Natalya A.; (21) International Application Number: 6214 Avalon Drive, Wilmington, Massachusetts 01887 PCT/US20 14/02 1796 (US). (22) International Filing Date: (74) Agents: MORRELL, Dennis G. et al; 271 Salem Street, 7 March 2014 (07.03.2014) Unit L, Woburn, Massachusetts 01801 (US). (25) Filing Language: English (81) Designated States (unless otherwise indicated, for every (26) Publication Language: English kind of national protection available): AE, AG, AL, AM, AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, (30) Priority Data: BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, 61/774,684 8 March 2013 (08.03.2013) US DO, DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, 61/774,773 8 March 2013 (08.03.2013) US HN, HR, HU, ID, IL, IN, IR, IS, JP, KE, KG, KN, KP, KR, 61/774,73 1 8 March 2013 (08.03.2013) us KZ, LA, LC, LK, LR, LS, LT, LU, LY, MA, MD, ME, 61/774,735 8 March 2013 (08.03.2013) us MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, NO, NZ, 61/774,740 8 March 2013 (08.03.2013) us OM, PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, RW, SA, 61/774,744 8 March 2013 (08.03.2013) us SC, SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, 61/774,746 8 March 2013 (08.03.2013) us TN, TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, ZM, 61/774,750 8 March 2013 (08.03.2013) us ZW. -

Circular of the Bureau of Standards No. 562: Bibliography of Research on Deuterium and Tritium Compounds 1945 and 1952
NBS CIRCULAR 562 Bibliography of Research on Deuterium and Tritium Compounds 1945 to 1952 UNITED STATES DEPARTMENT OF COMMERCE NATIONAL BUREAU OF STANDARDS PERIODICALS OF THE NATIONAL BUREAU OF STANDARDS (Published monthly) The National Bureau of Standards is engaged in fundamental and applied research in physics, chemistry, mathematics, and engineering. Projects are conducted in fifteen fields: electricity and electronics, optics and metrology, heat and power, atomic and radiation physics, chemistry, mechanics, organic and fibrous materials, metallurgy, mineral products, building technology, applied mathematics, data process¬ ing systems, cryogenic engineering, radio propagation, and radio standards. The Bureau has custody of the national standards of measurement and conducts research leading to the improvement of scientific and engineering standards and of techniques and methods of measurement. Testing methods and in¬ struments are developed; physical constants and properties of materials are determined; and technical processes are investigated. Journal of Research The Journal presents research papers by authorities in the specialized fields of physics, mathematics, chemistry, and engineering. Complete details of the work are presented, including laboratory data, experimental procedures, and theoretical and mathematical analyses. Annual subscription: domestic, $4.00; 25 cents additional for foreign mailing. Technical News Bulletin Summaries of current research at the National Bureau of Standards are published each month in the Technical News Bulletin. The articles are brief, with emphasis on the results of research, chosen on the basis of their scientific or technologic importance. Lists of all Bureau publications during the preceding month are given, including Research Papers, Handbooks, Applied Mathematics Series, Building Mate¬ rials and Structures Reports, Miscellaneous Publications, and Circulars. -

1. Public Health Statement
AMERICIUM 1 1. PUBLIC HEALTH STATEMENT This public health statement tells you about americium and the effects of exposure. The Environmental Protection Agency (EPA) identifies the most serious hazardous waste sites in the nation. These sites make up the National Priorities List (NPL) and are the sites targeted for long-term federal cleanup activities. Americium has been found in at least 8 of the 1,636 current or former NPL sites. However, the total number of NPL sites evaluated for americium is not known. As more sites are evaluated, the sites at which americium is found may increase. This information is important because exposure to americium may harm you and because these sites may be sources of exposure. When a substance is released from a large area, such as an industrial plant, or from a container, such as a drum or bottle, it enters the environment. This release does not always lead to exposure. You are normally exposed to a substance only when you come in contact with it. You may be exposed by breathing, eating, or drinking the substance, or by skin contact. However, since americium is radioactive, you can also be exposed to its radiation if you are near it. External or internal exposure to radiation may occur from natural or man-made sources. Naturally occurring sources of radiation are cosmic radiation from space or naturally occurring radioactive materials in our body or in soil, air, water, or building materials. Man-made sources of radiation are found in consumer products, industrial equipment, atom bomb fallout, and to a smaller extent, from hospital waste and nuclear reactors. -

Discovery of the Thallium, Lead, Bismuth, and Polonium Isotopes
Discovery of the thallium, lead, bismuth, and polonium isotopes C. Fry, M. Thoennessen∗ National Superconducting Cyclotron Laboratory and Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA Abstract Currently, forty-two thallium, forty-two lead, forty-one bismuth, and forty-two polonium isotopes have so far been observed; the discovery of these isotopes is discussed. For each isotope a brief summary of the first refereed publication, including the production and identification method, is presented. ∗Corresponding author. Email address: [email protected] (M. Thoennessen) Preprint submitted to Atomic Data and Nuclear Data Tables October 6, 2011 Contents 1. Introduction . 2 2. 176−217Tl ............................................................................................. 3 3. 179−220Pb............................................................................................. 14 4. 184−224Bi ............................................................................................. 22 5. 186−227Po ............................................................................................. 31 6. Summary ............................................................................................. 39 References . 39 Explanation of Tables . 47 7. Table 1. Discovery of thallium, lead, bismuth, and polonium isotopes . 47 Table 1. Discovery of thallium, lead, bismuth, and polonium. See page 47 for Explanation of Tables . 48 1. Introduction The discovery of thallium, lead, bismuth, and polonium -

Chapter 16 Nuclear Chemistry
Chapter 16 275 Chapter 16 Nuclear Chemistry Review Skills 16.1 The Nucleus and Radioactivity Nuclear Stability Types of Radioactive Emissions Nuclear Reactions and Nuclear Equations Rates of Radioactive Decay Radioactive Decay Series The Effect of Radiation on the Body 16.2 Uses of Radioactive Substances Medical Uses Carbon-14 Dating Other Uses for Radioactive Nuclides 16.3 Nuclear Energy Nuclear Fission and Electric Power Plants Nuclear Fusion and the Sun Special Topic 16.1: A New Treatment for Brain Cancer Special Topic 16.2: The Origin of the Elements Chapter Glossary Internet: Glossary Quiz Chapter Objectives Review Questions Key Ideas Chapter Problems 276 Study Guide for An Introduction to Chemistry Section Goals and Introductions Section 16.1 The Nucleus and Radioactivity Goals To introduce the new terms nucleon, nucleon number, and nuclide. To show the symbolism used to represent nuclides. To explain why some nuclei are stable and others not. To provide you with a way of predicting nuclear stability. To describe the different types of radioactive decay. To show how nuclear reactions are different from chemical reactions. To show how nuclear equations are different from chemical equations. To show how the rates of radioactive decay can be described with half-life. To explain why short-lived radioactive atoms are in nature. To describe how radiation affects our bodies.. This section provides the basic information that you need to understand radioactive decay. It will also help you understand the many uses of radioactive atoms, including how they are used in medicine and in electricity generation. Section 16.2 Uses of Radioactive Substances Goal: To describe many of the uses of radioactive atoms, including medical uses, archaeological dating, smoke detectors, and food irradiation. -

Naturally Occurring Radioactive Materials (NORM) in Arizona by Jon E
Naturally Occurring Radioactive Materials (NORM) in Arizona by Jon E. Spencer Arizona Geological Survey Open-File Report 02-13 September 2002 11 pages Arizona Geological Survey 416 W. Congress St., #100, Tucson, Arizona 85701 NATURALLY OCCURRING RADIOACTIVE MATERIALS (NORM) IN ARIZONA Jon Spencer Senior Geologist Arizona Geological Survey 416 W. Congress St., #100 Tucson, AZ 85701 INTRODUCTION Uranium-238 and other radioactive isotopes (radioisotopes) are present in small concentrations in all geologic materials. In a tiny fraction of these materials, such as uranium ore, radioisotope concentrations are greatly elevated. A much larger fraction of geologic materials contain slightly elevated concentrations of radioisotopes, but the radiation produced by these materials is far less than for uranium ore. The purpose of this brief report is to summarize the distribution, geologic association, and uranium concentration of naturally occurring radioactive materials (NORM) in Arizona, with emphasis on those materials that contain only slightly elevated concentrations of uranium. The bedrock geology of Arizona is characterized by a great diversity of rock types that were produced by a complex geologic history over the past 1.8 billion years. The concentrations of all of the chemical elements are highly variable in these different rock types. Elements that are usually present in small concentrations, known as trace elements, include the radioactive elements uranium and thorium. RADIOISOTOPES Most of the radioactivity in Earth’s crust is produced by uranium, thorium, their radioactive daughter products, and potassium. Potassium, a common and widespread element, is only very weakly radioactive and does not decay into radioactive daughter isotopes. Thorium is generally more abundant in crustal rocks than uranium, but its distribution and significance in Arizona are not as well understood as for uranium. -

The Radiochemistry of Bismuth
NAS-NS-3061 RA OFBISMUTH NUCLEAR SCIENCE SERIES National Academy of Sciences - National Research Council Published by Technical Information Center ENERGY RESEARCH AND DEVELOPMENT ADMINISTRATION COMMITTEE ON NUCLEAR SCIENCE John Huizenga, Chairman, Nuclear WrUcture Re=arch Laboratory Thomas A. Tombrello, Vice Chairman, California institute of T=hnology C. K. Reed, Executive Secretary,Netional Academy of Sciences Lowell M. Bollinger, Argonne Nationel Laboratow Peggy Dyer, UnivarsiW of Washington Rusaall Heath, Aerojet Nuclear Co., Inc. Roy K. Middlaton, University of Pennsylvania 1: Lon Morgan, Columbie Scientific Industries G. Davis O’Kelley, Oek Ridge National Laboratow G. C. Phillips, Rice University Henry N. Wagner, Jr., The Johns Hopkins Medial Institutions Joseph Wen~, Brookhaven National Laboratory Sheldon’ Wolff, University of California Chien-Shiung Wu, Columbia Univar?@ Alexander Zuckar, Oak Ridga National Laborato~ Liaison Members William S. Rodney, National science Foundation George L. ROWS, Energy Research and Development Admini-ration SUBCOMMITTEE ON RAD1OCHEMISTRY G. Davis O’Kelley, Chairmsrr, Oak Ridge National Laboratory Glen E. Gordon, UnivwsiW of Maryler& ‘“- ,-. Rolfa H. Hw*r, Rutgers Univemity John A. Miskel, Lawrence Livermore LaboratoW Harold A. O’Brien, Jr., Los Alamos Scientific Laboratory Richard W. Perkins. Bettafle Pacific Northwest Laboratories Andrew F. Stehney, Argonne National Laboratory Kurt Wotfsbarg, Los Alanros Scientific Laboratow LiaisonMembers ~ John L. Burnatte, Energy Research and Davelopmant Administration FTed Findeis, National Scienca Foundation i.,.~.. Radiochemistry of Bismuth Kashinath S. Bhatki Tata Instituteof Fundamental Research Homi Bhabha Road, Bombay 400005 and Bhabha Atomic ResearchC-entre Trornbay,Bombay 400085 (India) Prepared for Subcommittee on Radiochemistry National Academy of Sciences - Natiorial Research Council IssuanceDate:September 1977 Published by Technical 1nform,ation center ENERGY RESEARCH AND DEVELOPMENT ADMINISTRATION Price$4.75.Availablefrom: NationalTechnicalInformationservice U. -

Electrodialysis System
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2014/138600 Al 12 September 2014 (12.09.2014) P O P C T (51) International Patent Classification: 61/774,723 8 March 2013 (08.03.2013) US CUP 7/ 0 (2006.01) 61/793,336 15 March 2013 (15.03.2013) US (21) International Application Number: (71) Applicant: XYLECO, INC. [US/US]; 271 Salem Street, PCT/US2014/021815 Unit E, Woburn, Massachusetts 01801 (US). (22) International Filing Date: (72) Inventors: MEDOFF, Marshall; 90 Addington Road, 7 March 2014 (07.03.2014) Brookline, Massachusetts 02445 (US). MASTERMAN, Thomas Craig; 26 Linden Street, Brookline, Massachu Filing Language: English setts 02445 (US). MUKHERJEE, Maia Stapleton; 3 Re Publication Language: English gis Road, Arlington, Massachusetts 02474 (US). COOPER, Christopher; 96 New Street, Rehoboth, Mas (30) Priority Data: sachusetts 02769 (US). 61/774,684 8 March 2013 (08.03.2013) US 61/774,773 8 March 2013 (08.03.2013) US (74) Agent: MORRELL, Dennis G.; XYLECO, INC., 271 61/774,73 1 8 March 2013 (08.03.2013) u s Salem Street, Unit E, Woburn, Massachusetts 01801 (US). 61/774,735 8 March 2013 (08.03.2013) u s (81) Designated States (unless otherwise indicated, for every 61/774,740 8 March 2013 (08.03.2013) u s kind of national protection available): AE, AG, AL, AM, 61/774,744 8 March 2013 (08.03.2013) u s AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, 61/774,746 -

Assessment of Doses to the Public from Ingested Radionuclides
ASSESSMENT OF DOSES TO THE PUBLIC FROM INGESTED RADIONUCLIDES The following States are Members of the International Atomic Energy Agency: AFGHANISTAN HAITI PARAGUAY ALBANIA HOLY SEE PERU ALGERIA HUNGARY PHILIPPINES ARGENTINA ICELAND POLAND ARMENIA INDIA PORTUGAL AUSTRALIA INDONESIA QATAR AUSTRIA IRAN, ISLAMIC REPUBLIC OF REPUBLIC OF MOLDOVA BANGLADESH IRAQ ROMANIA BELARUS IRELAND RUSSIAN FEDERATION BELGIUM ISRAEL SAUDI ARABIA BOLIVIA ITALY SENEGAL BOSNIA AND JAMAICA SIERRA LEONE HERZEGOVINA JAPAN SINGAPORE BRAZIL JORDAN SLOVAKIA BULGARIA KAZAKHSTAN SLOVENIA BURKINA FASO KENYA SOUTH AFRICA CAMBODIA KOREA, REPUBLIC OF SPAIN CAMEROON KUWAIT SRI LANKA CANADA LATVIA SUDAN CHILE LEBANON SWEDEN CHINA LIBERIA SWITZERLAND COLOMBIA LIBYAN ARAB JAMAHIRIYA SYRIAN ARAB REPUBLIC COSTA RICA LIECHTENSTEIN THAILAND COTE D’IVOIRE LITHUANIA THE FORMER YUGOSLAV CROATIA LUXEMBOURG REPUBLIC OF MACEDONIA CUBA MADAGASCAR TUNISIA CYPRUS MALAYSIA TURKEY CZECH REPUBLIC MALI UGANDA DEMOCRATIC REPUBLIC MALTA UKRAINE OF THE CONGO MARSHALL ISLANDS UNITED ARAB EMIRATES DENMARK MAURITIUS UNITED KINGDOM OF DOMINICAN REPUBLIC MEXICO GREAT BRITAIN AND ECUADOR MONACO NORTHERN IRELAND EGYPT MONGOLIA UNITED REPUBLIC EL SALVADOR MOROCCO OF TANZANIA ESTONIA MYANMAR UNITED STATES ETHIOPIA NAMIBIA OF AMERICA FINLAND NETHERLANDS URUGUAY FRANCE NEW ZEALAND UZBEKISTAN GABON NICARAGUA VENEZUELA GEORGIA NIGER VIET NAM GERMANY NIGERIA YEMEN GHANA NORWAY YUGOSLAVIA GREECE PAKISTAN ZAMBIA GUATEMALA PANAMA ZIMBABWE The Agency’s Statute was approved on 23 October 1956 by the Conference on the Statute of the IAEA held at United Nations Headquarters, New York; it entered into force on 29 July 1957. The Headquarters of the Agency are situated in Vienna. Its principal objective is “to accelerate and enlarge the contribution of atomic energy to peace, health and prosperity throughout the world’’. -

High-Level Radioactive Waste Management: the Nuclear Dilemma
University of Kentucky UKnowledge Law Faculty Scholarly Articles Law Faculty Publications 1979 High-Level Radioactive Waste Management: The Nuclear Dilemma Richard C. Ausness University of Kentucky College of Law, [email protected] Follow this and additional works at: https://uknowledge.uky.edu/law_facpub Part of the Energy and Utilities Law Commons Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Recommended Citation Richard Ausness, High-Level Radioactive Waste Management: The Nuclear Dilemma, 1979 Wis. L. Rev. 707 (1979). This Article is brought to you for free and open access by the Law Faculty Publications at UKnowledge. It has been accepted for inclusion in Law Faculty Scholarly Articles by an authorized administrator of UKnowledge. For more information, please contact [email protected]. High-Level Radioactive Waste Management: The Nuclear Dilemma Notes/Citation Information Wisconsin Law Review, Vol. 1979, No. 3 (1979), pp. 707-767 This article is available at UKnowledge: https://uknowledge.uky.edu/law_facpub/326 ARTICLES HIGH-LEVEL RADIOACTIVE WASTE MANAGEMENT: THE NUCLEAR DILEMMA RICHARD AUSNESS * INTRODUCTION I. RADIOACTIVE WASTE: AN OVERVIEW 708 A. The Hazards of Radiation 712 1. THE SOMATIC EFFECTS OF RADIATION 713 a. External exposure to radiation 714 b. Internal exposure to radiation 714 2. THE GENETIC EFFECTS OF RADIATION 715 B. The Nuclear Fuel Cycle 716 C. Problem Areas 718 1. URANIUM MILL TAILINGS 719 2. ROUTINE EMISSIONS FROM NUCLEAR POWER PLANTS 720 3. LOW-LEVEL WASTE 724 II. HIGH-LEVEL NUCLEAR WASTE MANAGEMENT 727 A. High-Level Nuclear Waste . ...... 728 1. -
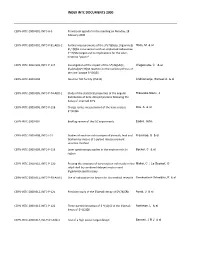
Index Intc Documents 2000
INDEX INTC DOCUMENTS 2000 CERN-INTC-2000-001, INTC-A-3 Provisional agenda for the meeting on Monday, 28 February 2000 CERN-INTC-2000-002, INTC-P-91-ADD-2 Further measurements of the $^{7}$Be(p, $\gamma$) Hass, M & al $\,^{8}$B cross section with an implanted radioactive $^{7}$Be target and its implications for the solar- neutrino "puzzle" CERN-INTC-2000-003, INTC-P-117 Investigation of the impact of the $^{39}$Ar(n, Wagemans, C & al $\alpha$)$^{36}$S reaction on the nucleosynthesis of the rare isotope $^{36}$S CERN-INTC-2000-004 Neutron TOF facility (PS213) Andriamonje, Samuel A & al CERN-INTC-2000-005, INTC-P-74-ADD-1 Study of the statistical properties of the angular Ríkovská-Stone, J distribution of beta-delayed protons following the decay of oriented KrFe CERN-INTC-2000-006, INTC-P-118 Charge radius measurement of the halo nucleus Dax, A & al $^{11}$Li CERN-INTC-2000-007 Backlog review of the ISC experiments Eades, John CERN-INTC-2000-008, INTC-I-31 Studies of neutron-rich isotopes of bismuth, lead and Franchoo, S & al thallium by means of a pulsed release element selective method CERN-INTC-2000-009, INTC-P-119 Laser spectroscopy studies in the neutron-rich Sn Becker, C & al region CERN-INTC-2000-010, INTC-P-120 Probing the structure of very neutron-rich nuclei in the Miehé, C ; Le Scornet, G sd-pf shell by combined delayed neutron and $\gamma$ spectroscopy CERN-INTC-2000-011, INTC-P-90-Add-1 Use of radioactive ion beams for bio-medical research Senekowitsch-Schmidtke, R & al CERN-INTC-2000-012, INTC-P-121 Precision study of the $\beta$-decay