DOCSLIB.ORG

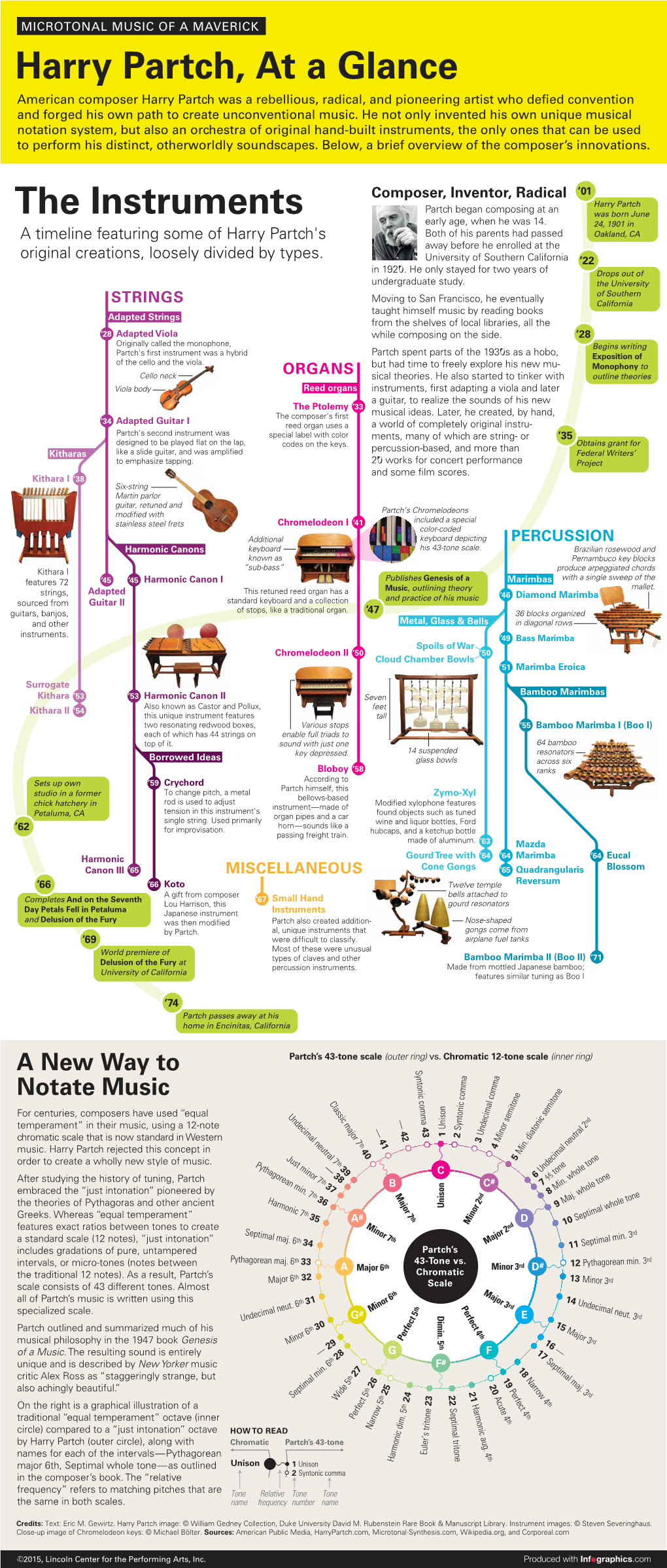
Harry Partch, at a Glance the Instruments

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Harry Partch, at a Glance the Instruments MICROTONAL MUSIC OF A MAVERICK Harry Partch, At a Glance American composer Harry Partch was a rebellious, radical, and pioneering artist who defied convention and forged his own path to create unconventional music. He not only invented his own unique musical notation system, but also an orchestra of original hand-built instruments, the only ones that can be used to perform his distinct, otherworldly soundscapes. Below, a brief overview of the composer’s innovations. TIMELINE Composer, Inventor, Radical ’01 Harry Partch Partch began composing at an The Instruments was born June early age, when he was 14. 24, 1901 in A timeline featuring some of Harry Partch's Both of his parents had passed Oakland, CA away before he enrolled at the original creations, loosely divided by types. University of Southern California ’22 in 1920. He only stayed for two years of Drops out of undergraduate study. the University Moving to San Francisco, he eventually of Southern STRINGS California taught himself music by reading books Adapted Strings from the shelves of local libraries, all the ’28 Adapted Viola while composing on the side. ’28 Originally called the monophone, Begins writing Partch's first instrument was a hybrid Partch spent parts of the 1930s as a hobo, Exposition of of the cello and the viola. but had time to freely explore his new mu- Monophony to Cello neck ORGANS sical theories. He also started to tinker with outline theories Viola body Reed organs instruments, first adapting a viola and later a guitar, to realize the sounds of his new The Ptolemy ’33 The composer's first musical ideas. Later, he created, by hand, ’34 Adapted Guitar I reed organ uses a a world of completely original instru- Partch's second instrument was special label with color ments, many of which are string- or ’35 designed to be played flat on the lap, codes on the keys. percussion-based, and more than Obtains grant for Kitharas like a slide guitar, and was amplified Federal Writers’ to emphasize tapping. 20 works for concert performance Project and some film scores. Kithara I ’38 Six-string Martin parlor guitar, retuned and Partch’s Chromelodeons modified with included a special stainless steel frets Chromelodeon I ’41 color-coded Additional keyboard depicting PERCUSSION Harmonic Canons keyboard his 43-tone scale. Brazilian rosewood and known as Pernambuco key blocks Kithara I ”sub-bass” produce arpeggiated chords with a single sweep of the features 72 ’45 ’45 Harmonic Canon I Publishes Genesis of a Marimbas Music, outlining theory mallet. strings, Adapted This retuned reed organ has a and practice of his music ‘46 Diamond Marimba sourced from Guitar II standard keyboard and a collection guitars, banjos, of stops, like a traditional organ. ’47 36 blocks organized and other Metal, Glass & Bells in diagonal rows instruments. ’49 Bass Marimba Spoils of War Chromelodeon II ’50 ’50 Cloud Chamber Bowls ’51 Marimba Eroica Surrogate Bamboo Marimbas Kithara ’53 ’53 Harmonic Canon II Seven Also known as Castor and Pollux, feet Kithara II ’54 this unique instrument features tall two resonating redwood boxes, Various stops ’55 Bamboo Marimba I (Boo I) each of which has 44 strings on enable full triads to top of it. sound with just one 64 bamboo key depressed. 14 suspended resonators Borrowed Ideas glass bowls across six Bloboy ’58 ranks According to Sets up own ’59 Crychord Partch himself, this studio in a former To change pitch, a metal Zymo-Xyl bellows-based rod is used to adjust Modified xylophone features chick hatchery in instrument—made of tension in this instrument's found objects such as tuned Petaluma, CA organ pipes and a car single string. Used primarily wine and liquor bottles, Ford horn—sounds like a ’62 for improvisation. hubcaps, and a ketchup bottle passing freight train. made of aluminum. ’63 Mazda Harmonic Gourd Tree with ’64 ’64 Marimba ’64 Eucal Canon III ’65 MISCELLANEOUS Cone Gongs ’65 Quadrangularis Blossom ’66 ’66 Koto Twelve temple Reversum A gift from composer bells attached to Completes And on the Seventh ’67 Small Hand Lou Harrison, this gourd resonators Day Petals Fell in Petaluma Japanese instrument Instruments and Delusion of the Fury was then modified Partch also created addition- Nose-shaped by Partch. al, unique instruments that gongs come from ’69 were difficult to classify. airplane fuel tanks World premiere of Most of these were unusual types of claves and other Bamboo Marimba II (Boo II) ’71 Delusion of the Fury at percussion instruments. Made from mottled Japanese bamboo; University of California features similar tuning as Boo I ’74 Partch passes away at his home in Encinitas, California Partch’s 43-tone scale (outer ring) vs. Chromatic 12-tone scale (inner ring) A New Way to Syntonic comma Notate Music Classic major 7 For centuries, composers have used “equal Undecimal neutral 7 — nd 43 Unison temperament” in their music, using a 12-note — Syntonic comma 42 Undecimal comma 1 2 chromatic scale that is now standard in Western 41 Minor semitone th 3 music. Harry Partch rejected this concept in 40 4 Min. diatonic semitone Just minor 7 5 order to create a wholly new style of music. th Pythagorean min. 7 — 39 C Undecimal tone neutral 2 38 6 4 ⁄5 After studying the history of tuning, Partch th 37 B C# 7 Min. whole tone embraced the “just intonation” pioneered by th Major 7 8 Harmonic 7 36 nd Maj. whole tone the theories of Pythagoras and other ancient Unison 9 th Greeks. Whereas “equal temperament” 35 A# th D Septimal whole tone Minor 2 10 features exact ratios between tones to create Minor 7 nd Septimal maj. 6 rd a standard scale (12 notes), “just intonation” th th 34 Major 2 11 Septimal min. 3 includes gradations of pure, untampered Partch’s intervals, or micro-tones (notes between Pythagorean maj. 6th 33 43-Tone vs. Pythagorean min. 3rd A Major 6th Minor 3rd D# 12 the traditional 12 notes). As a result, Partch’s Chromatic Major 6th 32 13 Minor 3rd scale consists of 43 different tones. Almost Scale th Major 3 all of Partch’s music is written using this th 31 14 Perfect 4 rd Undecimal neut. 3 Minor 6 th specialized scale. # Dimin. 5 Undecimal neut. 6 G E rd 15 Partch outlined and summarized much of his th 30 th Major 3 Perfect 5 rd musical philosophy in the 1947 book Genesis Minor 6 th 16 29 of a Music. The resulting sound is entirely G F 17 — — 28 th # Septimal maj. 3 unique and is described by New Yorker music F 18 27 critic Alex Ross as “staggeringly strange, but th 19 Narrow 4 26 20 Perfect 4 also achingly beautiful.” th 21 25 22 rd Acute 4 Septimal min. 6 th Wide 5 24 Harmonic aug. 4 th 23 On the right is a graphical illustration of a th Septimal tritone th Perfect 5 traditional “equal temperament” octave (inner th Narrow 5 circle) compared to a “just intonation” octave HOW TO READ by Harry Partch (outer circle), along with Chromatic Partch’s 43-tone Euler’s tritone names for each of the intervals—Pythagorean th Harmonic dim. 5 major 6th, Septimal whole tone—as outlined Unison 1 Unison in the composer’s book. The “relative 2 Syntonic comma frequency” refers to matching pitches that are Tone Relative Tone Tone the same in both scales. name frequency number name Credits: Text: Eric M. Gewirtz. Harry Partch image: © William Gedney Collection, Duke University David M. Rubenstein Rare Book & Manuscript Library. Instrument images: © Steven Severinghaus. Close-up image of Chromelodeon keys: © Michael Bölter. Sources: American Public Media, HarryPartch.com, Microtonal-Synthesis.com, Wikipedia.org, and Corporeal.com ©2015, Lincoln Center for the Performing Arts, Inc..
Load more

Recommended publications
  • Intervals and Transposition
    CHAPTER 3 Intervals and Transposition Interval Augmented and Simple Intervals TOPICS Octave Diminished Intervals Tuning Systems Unison Enharmonic Intervals Melodic Intervals Perfect, Major, and Minor Tritone Harmonic Intervals Intervals Inversion of Intervals Transposition Consonance and Dissonance Compound Intervals IMPORTANT Tone combinations are classifi ed in music with names that identify the pitch relationships. CONCEPTS Learning to recognize these combinations by both eye and ear is a skill fundamental to basic musicianship. Although many different tone combinations occur in music, the most basic pairing of pitches is the interval. An interval is the relationship in pitch between two tones. Intervals are named by the Intervals number of diatonic notes (notes with different letter names) that can be contained within them. For example, the whole step G to A contains only two diatonic notes (G and A) and is called a second. Figure 3.1 & ww w w Second 1 – 2 The following fi gure shows all the numbers within an octave used to identify intervals: Figure 3.2 w w & w w w w 1ww w2w w3 w4 w5 w6 w7 w8 Notice that the interval numbers shown in Figure 3.2 correspond to the scale degree numbers for the major scale. 55 3711_ben01877_Ch03pp55-72.indd 55 4/10/08 3:57:29 PM The term octave refers to the number 8, its interval number. Figure 3.3 w œ œ w & œ œ œ œ Octavew =2345678=œ1 œ w8 The interval numbered “1” (two notes of the same pitch) is called a unison. Figure 3.4 & 1 =w Unisonw The intervals that include the tonic (keynote) and the fourth and fi fth scale degrees of a Perfect, Major, and major scale are called perfect.
    [Show full text]
  • The Devil's Interval by Jerry Tachoir
    Sound Enhanced Hear the music example in the Members Only section of the PAS Web site at www.pas.org The Devil’s Interval BY JERRY TACHOIR he natural progression from consonance to dissonance and ii7 chords. In other words, Dm7 to G7 can now be A-flat m7 to resolution helps make music interesting and satisfying. G7, and both can resolve to either a C or a G-flat. Using the TMusic would be extremely bland without the use of disso- other dominant chord, D-flat (with the basic ii7 to V7 of A-flat nance. Imagine a world of parallel thirds and sixths and no dis- m7 to D-flat 7), we can substitute the other relative ii7 chord, sonance/resolution. creating the progression Dm7 to D-flat 7 which, again, can re- The prime interval requiring resolution is the tritone—an solve to either a C or a G-flat. augmented 4th or diminished 5th. Known in the early church Here are all the possibilities (Note: enharmonic spellings as the “Devil’s interval,” tritones were actually prohibited in of- were used to simplify the spelling of some chords—e.g., B in- ficial church music. Imagine Bach’s struggle to take music stead of C-flat): through its normal progression of tonic, subdominant, domi- nant, and back to tonic without the use of this interval. Dm7 G7 C Dm7 G7 Gb The tritone is the characteristic interval of all dominant bw chords, created by the “guide tones,” or the 3rd and 7th. The 4 ˙ ˙ w ˙ ˙ tritone interval can be resolved in two types of contrary motion: &4˙ ˙ w ˙ ˙ bbw one in which both notes move in by half steps, and one in which ˙ ˙ w ˙ ˙ b w both notes move out by half steps.
    [Show full text]
  • Andrián Pertout
    Andrián Pertout Three Microtonal Compositions: The Utilization of Tuning Systems in Modern Composition Volume 1 Submitted in partial fulfilment of the requirements of the degree of Doctor of Philosophy Produced on acid-free paper Faculty of Music The University of Melbourne March, 2007 Abstract Three Microtonal Compositions: The Utilization of Tuning Systems in Modern Composition encompasses the work undertaken by Lou Harrison (widely regarded as one of America’s most influential and original composers) with regards to just intonation, and tuning and scale systems from around the globe – also taking into account the influential work of Alain Daniélou (Introduction to the Study of Musical Scales), Harry Partch (Genesis of a Music), and Ben Johnston (Scalar Order as a Compositional Resource). The essence of the project being to reveal the compositional applications of a selection of Persian, Indonesian, and Japanese musical scales utilized in three very distinct systems: theory versus performance practice and the ‘Scale of Fifths’, or cyclic division of the octave; the equally-tempered division of the octave; and the ‘Scale of Proportions’, or harmonic division of the octave championed by Harrison, among others – outlining their theoretical and aesthetic rationale, as well as their historical foundations. The project begins with the creation of three new microtonal works tailored to address some of the compositional issues of each system, and ending with an articulated exposition; obtained via the investigation of written sources, disclosure
    [Show full text]
  • Boris's Bells, by Way of Schubert and Others
    Boris's Bells, By Way of Schubert and Others Mark DeVoto We define "bell chords" as different dominant-seventh chords whose roots are separated by multiples of interval 3, the minor third. The sobriquet derives from the most famous such pair of harmonies, the alternating D7 and AI? that constitute the entire harmonic substance of the first thirty-eight measures of scene 2 of the Prologue in Musorgsky's opera Boris Godunov (1874) (example O. Example 1: Paradigm of the Boris Godunov bell succession: AJ,7-D7. A~7 D7 '~~&gl n'IO D>: y 7 G: y7 The Boris bell chords are an early milestone in the history of nonfunctional harmony; yet the two harmonies, considered individually, are ofcourse abso­ lutely functional in classical contexts. This essay traces some ofthe historical antecedents of the bell chords as well as their developing descendants. Dominant Harmony The dominant-seventh chord is rightly recognized as the most unambiguous of the essential tonal resources in classical harmonic progression, and the V7-1 progression is the strongest means of moving harmony forward in immediate musical time. To put it another way, the expectation of tonic harmony to follow a dominant-seventh sonority is a principal component of forehearing; we assume, in our ordinary and long-tested experience oftonal music, that the tonic function will follow the dominant-seventh function and be fortified by it. So familiar is this everyday phenomenon that it hardly needs to be stated; we need mention it here only to assert the contrary case, namely, that the dominant-seventh function followed by something else introduces the element of the unexpected.
    [Show full text]
  • The Development of Duke Ellington's Compositional Style: a Comparative Analysis of Three Selected Works
    University of Kentucky UKnowledge University of Kentucky Master's Theses Graduate School 2001 THE DEVELOPMENT OF DUKE ELLINGTON'S COMPOSITIONAL STYLE: A COMPARATIVE ANALYSIS OF THREE SELECTED WORKS Eric S. Strother University of Kentucky, [email protected] Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Recommended Citation Strother, Eric S., "THE DEVELOPMENT OF DUKE ELLINGTON'S COMPOSITIONAL STYLE: A COMPARATIVE ANALYSIS OF THREE SELECTED WORKS" (2001). University of Kentucky Master's Theses. 381. https://uknowledge.uky.edu/gradschool_theses/381 This Thesis is brought to you for free and open access by the Graduate School at UKnowledge. It has been accepted for inclusion in University of Kentucky Master's Theses by an authorized administrator of UKnowledge. For more information, please contact [email protected]. ABSTRACT OF THESIS THE DEVELOPMENT OF DUKE ELLINGTON’S COMPOSITIONAL STYLE: A COMPARATIVE ANALYSIS OF THREE SELECTED WORKS Edward Kennedy “Duke” Ellington’s compositions are significant to the study of jazz and American music in general. This study examines his compositional style through a comparative analysis of three works from each of his main stylistic periods. The analyses focus on form, instrumentation, texture and harmony, melody, tonality, and rhythm. Each piece is examined on its own and their significant features are compared. Eric S. Strother May 1, 2001 THE DEVELOPMENT OF DUKE ELLINGTON’S COMPOSITIONAL STYLE: A COMPARATIVE ANALYSIS OF THREE SELECTED WORKS By Eric Scott Strother Richard Domek Director of Thesis Kate Covington Director of Graduate Studies May 1, 2001 RULES FOR THE USE OF THESES Unpublished theses submitted for the Master’s degree and deposited in the University of Kentucky Library are as a rule open for inspection, but are to be used only with due regard to the rights of the authors.
    [Show full text]
  • Frequency Ratios and the Perception of Tone Patterns
    Psychonomic Bulletin & Review 1994, 1 (2), 191-201 Frequency ratios and the perception of tone patterns E. GLENN SCHELLENBERG University of Windsor, Windsor, Ontario, Canada and SANDRA E. TREHUB University of Toronto, Mississauga, Ontario, Canada We quantified the relative simplicity of frequency ratios and reanalyzed data from several studies on the perception of simultaneous and sequential tones. Simplicity offrequency ratios accounted for judgments of consonance and dissonance and for judgments of similarity across a wide range of tasks and listeners. It also accounted for the relative ease of discriminating tone patterns by musically experienced and inexperienced listeners. These findings confirm the generality ofpre­ vious suggestions of perceptual processing advantages for pairs of tones related by simple fre­ quency ratios. Since the time of Pythagoras, the relative simplicity of monics of a single complex tone. Currently, the degree the frequency relations between tones has been consid­ of perceived consonance is believed to result from both ered fundamental to consonance (pleasantness) and dis­ sensory and experiential factors. Whereas sensory con­ sonance (unpleasantness) in music. Most naturally OCCUf­ sonance is constant across musical styles and cultures, mu­ ring tones (e.g., the sounds of speech or music) are sical consonance presumably results from learning what complex, consisting of multiple pure-tone (sine wave) sounds pleasant in a particular musical style. components. Terhardt (1974, 1978, 1984) has suggested Helmholtz (1885/1954) proposed that the consonance that relations between different tones may be influenced of two simultaneous complex tones is a function of the by relations between components of a single complex tone. ratio between their fundamental frequencies-the simpler For single complex tones, ineluding those of speech and the ratio, the more harmonics the tones have in common.
    [Show full text]
  • Early Experimental and Electronic Music
    Early Experimental and Electronic Music Today you will listen to early experimental and electronic music composed in the 1930s, ‘40s, and ‘50s. Think about the following questions as you listen to the music. 1. One of your listening assignments, “Valse Sentimentale,” is played by Clara Rockmore, a virtuoso on the theremin, an early electronic instrument. Look at the YouTube videos of Theremin and Clara Rockmore playing the theremin. How is the instrument played? Why has it been used only infrequently as a serious musical instrument? 2. When was the theremin developed and who was its inventor? 3. As an additional listening assignment, listen to “Good Vibrations” by the Beach Boys (in the listening for Monday). Where do you hear an electro-theremin, which is similar to the theremin, but easier to play? 4. What are the connections between the theremin and modern-day synthesizers? 5. What instrument is being played in “Oriason?” From your reading, what is unusual about the use of this instrument in this recording? 6. Watch the YouTube video of Thomas Bloch playing Messian piece on the Ondes-Martenot. How does is this instrument similar to but yet different from a piano? What does it have in common with the theremin. 6. People often think that experimental music is difficult and not beautiful. Is that true of all the music in these lessons? Is it true sometimes? Give examples. 7. The well-tempered scale usually used in Western music has 12 pitches in an octave. Well-tempered scale (12 pitches in an octave) In the section on Partch in Gann’s American Music in the Twentieth Century, Partch is said to have rebelled against the “acoustic lie” of the well-tempered scale.
    [Show full text]
  • The Effects of Musical Intervals from Consonant to Dissonant on the Neural Activity of Earthworms
    Columbus State University CSU ePress Theses and Dissertations Student Publications 2016 The Effects of Musical Intervals from Consonant to Dissonant on the Neural Activity of Earthworms Charley L. Weaver Follow this and additional works at: https://csuepress.columbusstate.edu/theses_dissertations Part of the Biology Commons Recommended Citation Weaver, Charley L., "The Effects of Musical Intervals from Consonant to Dissonant on the Neural Activity of Earthworms" (2016). Theses and Dissertations. 305. https://csuepress.columbusstate.edu/theses_dissertations/305 This Thesis is brought to you for free and open access by the Student Publications at CSU ePress. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of CSU ePress. THE EFFECTS OF MUSICAL INTERVALS FROM CONSONANT TO DISSONANT ON THE NEURAL ACTIVITY OF EARTHWORMS Charley L. Weaver COLUMBUS STATE UNIVERSITY THE EFFECTS OF MUSICAL INTERVALS FROM CONSONANT TO DISSONANT ON THE NEURAL ACTIVITY OF EARTHWORMS A THESIS SUBMITTED TO THE HONORS COLLEGE IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR HONORS IN THE DEGREE OF BACHELOR OF ARTS DEPARTMENT OF BIOLOGY COLLEGE OF LETTERS AND SCIENCES BY CHARLEY L. WEAVER COLUMBUS, GEORGIA 2016 THE EFFECTS OF MUSICAL INTERVALS FROM CONSONANT TO DISSONANT ON THE NEURAL ACTIVITY OF EARTHWORMS By Charley L. Weaver A Thesis Submitted to the HONORS COLLEGE In Partial Fulfillment of the Requirements For Honors in the Degree of BACHELOR OF ARTS BIOLOGY COLLEGE OF LETTERS AND SCIENCES Thesis Advisor Date Dr. Kathleen Hughes Committee Member Date Dr. Susan Tomkiewicz Honors College Dean ABSTRACT Music is generated through vibrations of a medium creating what is perceived as tone.
    [Show full text]
  • Musical Techniques
    Musical Techniques Musical Techniques Frequencies and Harmony Dominique Paret Serge Sibony First published 2017 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd John Wiley & Sons, Inc. 27-37 St George’s Road 111 River Street London SW19 4EU Hoboken, NJ 07030 UK USA www.iste.co.uk www.wiley.com © ISTE Ltd 2017 The rights of Dominique Paret and Serge Sibony to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2016960997 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78630-058-4 Contents Preface ........................................... xiii Introduction ........................................ xv Part 1. Laying the Foundations ............................ 1 Introduction to Part 1 .................................. 3 Chapter 1. Sounds, Creation and Generation of Notes ................................... 5 1.1. Physical and physiological notions of a sound .................. 5 1.1.1. Auditory apparatus ............................... 5 1.1.2. Physical concepts of a sound .......................... 7 1.1.3.
    [Show full text]
  • Tuning: at the Grcssroads
    WendyGarloo ?O. Box1024 Tuning:At the New YorkCit, New York 10276USA Grcssroads lntrodrciion planned the construction of instruments that per- formed within the new "tunitrg of choice," and all The arena o{ musical scales and tuning has cer_ publishedpapers or books demonstretingthe supe- tainly not been a quiet place to be for the past thlee dority of their new scales in at least some way over hundred yeals. But it might iust as well have beenif €qual temperament.The tradition has continued we iudge by the results: the same 12V2 equally with Yunik and Swi{t {1980),Blackwood (1982),and temperedscale established then as the best avail- the presentauthor (Milano 1986),and shows no able tuning compromise, by J. S. Bach and many sign of slowing down despite the apparent apathy otheis lHelrnholtz 1954j Apel 1972),remains to with which the musical mainstream has regularly this day essentially the only scale heard in Westem grceted eech new proposal. music. That monopoly crossesall musical styles, of course therc's a perf€ctly reasonable explana- {rom the most contemporary of jazz and av^rf,t' tion lor the mainstream's evident preferetrce to rc- "rut-bound" gardeclassical, and musical masteeieces from the main when by now there are at least past, to the latest technopop rock with fancy s)'n- a dozen clearly better-sounding ways to tune our thesizers,and everwvherein between.Instruments scales,i{ only for at least part of the time: it re' ol the symphonyorchestra a((empr with varyirrg quires a lot of effort ol several kinds. I'm typing this deSreesof successto live up ro lhe 100-centsemi manuscript using a Dvorak keyboard (lor the ffrst tone, even though many would find it inherently far time!), and I assureyou it's not easyto unlearn the easierto do otherwise: the stdngs to "lapse" into QWERTY habits of a lifetime, even though I can Pythagoieen tuning, the brass into several keys of akeady feel the actual superiodty of this unloved lust irtonation lBarbour 1953).And th€se easily but demonstrablv better kevboard.
    [Show full text]
  • A LIGHTWEIGHT NOTATION for PLAYING PIANO for FUN by R.J.A
    A LIGHTWEIGHT NOTATION FOR PLAYING PIANO FOR FUN by R.J.A. Buhr 1. INTRODUCTION Music notation gets in the way of the joy of making music on the piano that can be had without first spending thousands of hours at the keyboard to develop piano “wizardry,” meaning a combination of keyboard skill and mastery of music notation. The message of this document is the joy can be had, without any loss of musical substance, with no more wizardry than is required to read and play single melody lines. The vehicle is a lightweight notation I call PKP (for Picturing Keyboard Patterns) for annotating the core flow of harmony in interval terms above the staff. I developed the notation as an adult beginner with no training in music theory after becoming frustrated with the way music notation obscures the keyboard simplicity of harmony. That the notation has substance in spite of this humble origin is indicated by the following opinion of PKP provided by a music theorist specializing in improvisational music (see supplementary pages): “The hook ... , at least in my opinion, is that it's possible to attain a deep understanding of chords (and their constituent intervals) without recourse to Western notation. This has direct consequences for physical patterning, fingerings, etc. Essentially, your method combines the utility of a play-by-ear approach with the depth of a mathematically-informed theory of music.” PKP follows from two observations that anyone can make. One is the piano keyboard supplies only 12 piano keys to play all the notes of an octave that music notation describes in many more than 12 ways by key signatures and accidentals (sharps, flats, naturals).
    [Show full text]
  • Consonance & Dissonance
    UIUC Physics 406 Acoustical Physics of Music Consonance & Dissonance: Consonance: A combination of two (or more) tones of different frequencies that results in a musically pleasing sound. Why??? Dissonance: A combination of two (or more) tones of different frequencies that results in a musically displeasing sound. Why??? n.b. Perception of sounds is also wired into (different of) our emotional centers!!! Why???/How did this happen??? The Greek scholar Pythagoras discovered & studied the phenomenon of consonance & dissonance, using an instrument called a monochord (see below) – a simple 1-stringed instrument with a movable bridge, dividing the string of length L into two segments, x and L–x. Thus, the two string segments can have any desired ratio, R x/(L–x). (movable) L x x L When the monochord is played, both string segments vibrate simultaneously. Since the two segments of the string have a common tension, T, and the mass per unit length, = M/L is the same on both sides of the string, then the speed of propagation of waves on each of the two segments of the string is the same, v = T/, and therefore on the x-segment of string, the wavelength (of the fundamental) is x = 2x = v/fx and on the (L–x) segment of the string, we have Lx = 2(L–x) = v/fLx. Thus, the two frequencies associated with the two vibrating string segments x and L – x on either side of the movable bridge are: v f x 2x v f Lx 2L x - 1 - Professor Steven Errede, Department of Physics, University of Illinois at Urbana-Champaign, Illinois 2002 - 2017.
    [Show full text]