Swiss Sailing Team Athlete Portfolio Optimization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Team Portraits Emirates Team New Zealand - Defender
TEAM PORTRAITS EMIRATES TEAM NEW ZEALAND - DEFENDER PETER BURLING - SKIPPER AND BLAIR TUKE - FLIGHT CONTROL NATIONALITY New Zealand HELMSMAN HOME TOWN Kerikeri NATIONALITY New Zealand AGE 31 HOME TOWN Tauranga HEIGHT 181cm AGE 29 WEIGHT 78kg HEIGHT 187cm WEIGHT 82kg CAREER HIGHLIGHTS − 2012 Olympics, London- Silver medal 49er CAREER HIGHLIGHTS − 2016 Olympics, Rio- Gold medal 49er − 2012 Olympics, London- Silver medal 49er − 6x 49er World Champions − 2016 Olympics, Rio- Gold medal 49er − America’s Cup winner 2017 with ETNZ − 6x 49er World Champions − 2nd- 2017/18 Volvo Ocean Race − America’s Cup winner 2017 with ETNZ − 2nd- 2014 A class World Champs − 3rd- 2018 A class World Champs PATHWAY TO AMERICA’S CUP Red Bull Youth America’s Cup winner with NZL Sailing Team and 49er Sailing pre 2013. PATHWAY TO AMERICA’S CUP Red Bull Youth America’s Cup winner with NZL AMERICA’S CUP CAREER Sailing Team and 49er Sailing pre 2013. Joined team in 2013. AMERICA’S CUP CAREER DEFINING MOMENT IN CAREER Joined ETNZ at the end of 2013 after the America’s Cup in San Francisco. Flight controller and Cyclor Olympic success. at the 35th America’s Cup in Bermuda. PEOPLE WHO HAVE INFLUENCED YOU DEFINING MOMENT IN CAREER Too hard to name one, and Kiwi excelling on the Silver medal at the 2012 Summer Olympics in world stage. London. PERSONAL INTERESTS PEOPLE WHO HAVE INFLUENCED YOU Diving, surfing , mountain biking, conservation, etc. Family, friends and anyone who pushes them- selves/the boundaries in their given field. INSTAGRAM PROFILE NAME @peteburling Especially Kiwis who represent NZ and excel on the world stage. -

2010 VERKSAMHETSBERÄTTELSE Med Årsredovisning Glädje
– 1 – www.svensksegling.se 2010 VERKSAMHETSBERÄTTELSE med årsredovisning Glädje Laganda Uthållighet Ärlighet Frihet Miljö – 4 – Svenska Seglarförbundet (SSF) är ett av 70 specialidrottsförbund som är anslutet till Svenska Riksidrottsförbundet, RF, och ett av 35 olympiska specialförbund i Sveriges Olympiska Kommitté, SOK. SSF har cirka 127 900 medlemmar, fördelade på 412 klubbar, 17 distrikt och 84 klassförbund. Svenska Seglarförbundet af Pontins väg 6, 115 21 Stockholm Tel 08-459 09 90, fax 08-459 09 99 E-post [email protected], www.svensksegling.se Kansli Stefan Rahm, förbundsdirektör och sportchef Carina Petersson, kanslichef (10.1.2010-11.11.2010) Åsa Blomqvist-Jonsson, ekonomi och administration Jakob Gustafsson, juniorkoordinator Magnus Grävare, förbundskapten Jan Steven Johannessen, ass. förbundskapten Thomas Rahm, ass. förbundskapten, ansvarig TSC Anders Larzon, utbildningsansvarig Kjell Marthinsen, teknik- och mätansvarig Styrelse Lena Engström, ordförande Michael Persson, vice ordförande Johan Hedberg, kassör Charlotte Alexandersson Annika Ekman Fredrik Norén Victor Wallenberg Berndt Öjerborn Bilder Om ej annat anges: Svenska Seglarförbundet Omslag: Svenska Mästerskapet i 49er, Malmö 2010 Foto: Elke Cronenberg Bilduppslag insida: 1 RS Feva Fritiof och Hedvig Hedström, Långedrags SS, på väg att ta 4:e platsen på SM som arrangerades av hemmaklubben. Foto: Henrik Samuelsson 2 SM-mästaren i Laser heter Emil Cedergårdh. Foto: David Sandberg 3 SM i Express 4 C55 SM 5 SWE Sailing Teams Andreas Axelsson på världscuptävlingen i Weymouth. Foto: Onedition 6 Farr 30-VM Foto: Meredth Block 7 Kona SM i Malmö. Foto: Elke Cronenberg Produktion • Elke Cronenberg • Ansvarig utgivare: Svenska Seglarförbundet • Tryckt hos Elanders Sponsorer 2010 Leverantörer 2010 PANTONE 186 BLACK – 5 – Svenska Seglarförbundets:s styrelse (från vänster): Victor Wallenberg, Berndt Öjerborn, Annika Ekman, Michael Persson, Lena Engström, Charlotte Alexandersson, Johan Hedberg och Fredrik Norén. -

470 - Women - Overall Results
470 - Women - Overall Results Pos Nation Sail Crew Race Points Number 1 2 3 4 5 6 7 8 9 10 11 Total Net 1 AUT AUT 431 Lara Vadlau 2 (11) 1 5 1 5 1 11 4 2 2 45.00 34.00 Jolanta Ogar 2 NZL NZL 75 Jo Aleh (7) 5 6 2 5 1 4 2 3 5 12 52.00 45.00 Polly Powrie 3 GBR GBR 118 Hannah Mills 11 2 1 3 11 9 (14) 3 2 4 4 64.00 50.00 Saskia Clark 4 FRA FRA 9 Camille Lecointre 3 5 4 4 (24) 10 6 4 5 15 8 88.00 64.00 Hélène Defrance 5 SLO SLO 64 Tina Mrak 4 11 14 1 4 (15) 12 5 6 8 6 86.00 71.00 Veronika Macarol 6 NED NED 6 Michelle Broekhuizen 4 13 3 1 9 7 9 (17) 10 6 10 89.00 72.00 Marieke Jongens 7 USA USA Anne Haeger 14 7 2 3 7 4 2 6 (28) 14 16 103.00 75.00 1712 Briana Provancha DNF 8 JPN JPN 1 Ai Kondo Yoshida 7 (25) 4 10 3 12 5 16 14 3 14 113.00 88.00 Miho Yoshioka 9 GBR GBR 321 Christina Bassadone 16 (19) 3 5 12 2 8 13 12 1 18 109.00 90.00 Eilidh McIntyre 10 NED NED 216 Afrodite Kyranakou 1 10 5 (17) 14 8 15 1 13 7 20 111.00 94.00 Anneloes van Veen 11 RUS RUS 97 Alisa Kirilyuk 18 6 19 4 6 3 3 (22) 7 12 100.00 78.00 Liudmila Dmitrieva 12 BRA BRA 18 Renata Decnop 17 14 9 6 2 (28) 13 10 1 9 109.00 81.00 Isabel Swan DNF 13 BRA BRA 177 Fernanda Oliveira 1 3 16 (28) 8 6 7 15 8 17 109.00 81.00 Ana Luiza Barbachan UFD 14 GBR GBR 812 Anna Burnet 9 12 17 8 15 13 10 (19) 9 13 125.00 106.00 Flora Stewart 15 CHN CHN 619 Shasha Chen 6 9 2 6 (25) 18 19 21 20 11 137.00 112.00 Haiyan Gao 16 CHN CHN 616 Xiaomei XU 6 3 21 7 13 11 11 (25) 16 25 138.00 113.00 Ping Zhang 17 POL POL 11 Agnieszka Skrzypulec 15 18 13 2 16 16 (22) 8 21 10 141.00 119.00 Natalia Wojcik 18 CHN -

Seglingens Högsäsong
SVENSKSEGLING.SE Seglingens högsäsong HÖGSÄSONG FÖR SEGLINGEN är förstås som- med VM-brons och även topplaceringar på maren och i år har vi ännu en enastående VM i Laser. Också 29er VM i Gdynia bjöd på säsong bakom oss, fylld av fantastiska många framskjutna placeringar där Sverige seglingsupplevelser för såväl kappseglare, var representerat av hela 10 team med både semesterseglare som åskådare. Svenska ett brons totalt och inget mindre än ett guld i Seglarförbundets vision är ”Segling – Till- tjejklassen. gänglig för alla” och vår seglarsommar visar Det finns mycket att uppmärksamma och att seglingen också bjuder på mycket till- vi har både spets och bredd som vi skall måna gänglighet både för den som seglar själv om och stödja i sin vidare utveckling. eller för den som följer seglingen från land. ÄVEN SEGLARFÖRBUNDETS KANSLI och styrelse I JUNI BJÖD ÅF Offshore Race på en folkfest har utmärkt sig i sommar. Thomas Hansson- mitt i Stockholm med ett av de tuffaste Mild ägnar sig inte bara åt Plastimister och racen någonsin för de 225 startande. På Optimist för Havet utan passade på att knipa Marstrand kördes matchrace som tradi- ett EM-silver i OK-jolle i Kiel. Vår förbunds- tionen bjuder och även 10-årsjubileum för direktör Marie Björling Duell (Team Emer- Jr Cup på en av de bästa seglingsarenorna son) gjorde en respektingivande comeback i man kan tänka sig. årets VM i Match Racing och Lysekil Women’s I Skärhamn var det premiär som gav Match och tog sig med teamet till kvartsfinal i mersmak med Midsummer Match Cup för hård konkurrens under ytterligare ett enastå- mixade lag med två damer och två herrar i ende och välbesökt seglingsevent. -

Dossier De Presse SOF 2012
DOSSIER DE PRESSE 2012 Sommaire Le mot de Jean-Pierre Champion, Président de la Fédération Française de Voile ................................. 3 Le mot d’Hubert Falco, Président de la Communauté d’aggomération TPM ......................................... 4 Le mot d’accueil de Jacques Politi, maire de Hyères-Les-Palmiers ......................................................... 5 I. L’épreuve .............................................................................................................................................. 6 La SOF 2012, 4ème épreuve de la Coupe du Monde ISAF ..................................................................... 6 Les spécificités de la SOF 2012 ............................................................................................................ 7 Les enjeux spécifiques pour l’équipe de France .................................................................................. 8 La régate .............................................................................................................................................. 8 Le programme ..................................................................................................................................... 9 Les clés pour comprendre ................................................................................................................... 9 II. Les séries engagées ........................................................................................................................... 13 Synthèse des séries .......................................................................................................................... -
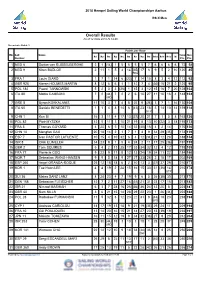
Manage2sail Report
2018 Hempel Sailing World Championships Aarhus RS:X Men Overall Results As of 12 AUG 2018 At 14:40 Discard rule: Global: 3. Points per Race Rk. Sail Name Total Net R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 M Number Pts. Pts. 1 NED 8 Dorian van RIJSSELBERGHE 2 1 (14) 1 5 8 5 5 7 6 6 6 6 72 58 2 NED 9 Kiran BADLOE 2 11 1 5 3 14 (35) 17 6 9 5 2 10 120 85 RDG 3 FRA 1 Louis GIARD 1 7 1 14 6 (20) 7 14 15 8 3 4 12 112 92 4 GBR 926 Kieran HOLMES MARTIN 8 12 6 6 1 1 12 7 4 (30) 15 21 2 125 95 5 POL 182 Pawel TARNOWSKI 5 2 3 3 (26) 1 15 3 12 15 16 7 20 128 102 6 ITA 88 Mattia CAMBONI 7 2 (44) 7 2 2 6 10 27 11 10 16 4 148 104 UFD 7 GRE 8 Byron KOKKALANIS 11 10 3 7 4 8 25 9 (26) 3 7 1 16 130 104 8 ITA 60 Daniele BENEDETTI 1 1 4 8 14 6 (41) 23 18 5 14 10 14 159 118 STP 9 CHN 1 Kun BI 16 3 11 4 17 13 (37) 20 21 7 1 5 8 163 126 10 POL 82 Piotr MYSZKA 12 5 11 3 10 21 19 8 13 10 (22) 3 18 155 133 11 FRA 3 Thomas GOYARD 4 20 6 5 10 14 35 (40) 16 4 2 14 170 130 12 CHN 10 Mengfan GAO 20 18 14 2 1 7 1 4 9 34 29 (35) 174 139 13 ESP 7 Ivan PASTOR LAFUENTE 10 15 4 10 32 6 4 12 (34) 21 12 28 188 154 14 ISR 8 Ofek ELIMELEH 34 23 9 1 5 4 24 2 11 17 25 (36) 191 155 15 GBR 2 Tom SQUIRES 5 4 2 13 25 17 33 (34) 32 12 4 12 193 159 16 FRA 77 Pierre le COQ 9 22 9 11 8 12 13 (24) 19 24 11 22 184 160 17 NOR 7 Sebastian WANG-HANSEN 9 9 5 18 9 27 27 (33) 28 2 18 17 202 169 18 ESP 260 Angel GRANDA-ROQUE 25 12 18 18 6 2 10 13 3 (37) 37 29 210 173 19 KOR 1 Tae Hoon LEE 4 4 19 2 24 15 16 15 30 31 (36) 14 210 174 STP 20 SUI 36 Mateo SANZ LANZ 8 28 23 4 7 19 9 6 5 36 (38) 30 213 175 -

Multala Retains World Title
Laser World September 2010 © Thom Touw Multala Retains World Title Laser ?Championship Round Up Laser Championship Round Up European Laser 4.7 Youths in Hourtin Up & Coming Champions © Mark Turner / RYA © Albert Cassio © NDK Photography COPYRIGHT AND LIABILITY No part of this publication may be reproduced without prior permission of the publishers. The articles and opinions in LaserWorld may not represent the official views of ILCA. The publishers do not accept any liability for their accuracy. 2 LaserWorld September 2010 © Aivar Kullamaa / European Championships & Trophy 2010 Croatians Take the Title in Tallinn Stipanovic & Mihelic Crowned European Laser Champions © Aivar Kullamaa / European Championships & Trophy 2010 Good weather conditions at Tallinn Bay welcomed was 5-12 knots and really shifty”, he said. Laser Standard and Laser Radial athletes on their first day of the European Championship & Trophy Tonci Stipanovic (CRO), won both races event. in his fleet and ended the day in second place with 27 points, while Geritzer was in With a southern wind of 4-7 m/s and partly cloudy third on 31 points. sky, the Laser Standard sailors started the event in three fleets. Milan Vujasinovic (CRO) won the In the Laser Radial, Mihelic again first race in the Yellow fleet while Yuval Botzer outperformed her competition, winning (ISR) enjoyed victory in the second race. In the both races in her fleet and strengthening Blue group, Malo Leseigneur (FRA) and Tom her leader position once more. Dobson Slingsby (AUS) were winners of the respective was 18 points behind in second place, races. In the Red fleet, which struggled with three while Evi Van Acker ended the day in general recalls and 12 black flag disqualifications third. -

F Nnwellemagazin Der Deutschen Finnsegler Vereinigung E.V
2019 F NNWELLEMAGAZIN DER DEUTSCHEN FINNSEGLER VEREINIGUNG E.V. (DFSV e.V.) - Finn Team Germany Nesselblatt Steinhude – Kultveranstaltung über vier Tage IDM in Friedrichshafen – Heiße Zeit am Bodensee Sailing World Championships – Tolle Bilder aus Aarhus 2019 28. Sept. – 4. Okt. 2019 Gestaltung + Redaktion MEID MEID + PARTNER GMBH Gunther-Plüschow-Str. 1 56743 Mendig Tel.: +49 2652 595259 - 0 Fax: +49 2652 595259 - 9 www.meidmeid.de [email protected] Vorwort © Robert Deaves Liebe Finnsegler und Freunde, vermeiden lassen. Bitte habt Verständnis Yacht-Club wird die Euromasters (11.– dafür, dass die von Adalbert Wiest ge- 15.09.2019) ausrichten; als Vorregatta ein für die künftige Reputation unserer pflegte Übersicht „RL-Termine 2019“ in bietet sich hier der Herbstpokal an. Alles Klasse einschneidendes Jahr liegt hinter der Rubrik „Rangliste“ unserer Homepage weitere findet ihr im Internet unter snyc. uns; euch allen dürfte nicht entgangen die einzig verbindliche ist. Das gilt auch de/regatten/finn-european-masters-2019 sein, dass die Finns ab 2024 den olympi- für die Folgejahre. Alle anderen Kalender, schen Segeldisziplinen fernbleiben sollen. Aufstellungen etc. sind stets nur vorläufig Und noch eine interessante Veranstaltung: Darüber, wie und zu welchem Zeitpunkt und unverbindlich. In 2020 wird bekanntlich die Worldmasters mit welchen – zumindest für mich nicht wieder in Holland stattfinden. Diejenigen, nachvollziehbaren – Allianzen die Ent- Im Regelwerk der für uns gültigen Rang- die das Revier schon mal kennen lernen scheidungsträger hier abgestimmt haben, listenordnung des DSV gibt es eine kleine möchten, sei die diesjährige holländische wird vermutlich nicht mehr aufgeklärt Änderung: Für 2019 und 2020 besteht Masters in der Zeit vom 5.–7.07.2019 in werden. -

470 INTERNATIONALE DRAFT Minutes
470 INTERNATIONALE DRAFT Minutes MINUTES 2018 General Assembly Meeting The General Assembly meeting of the 470 Internationale took place on Saturday 19 May 2018 at the Yacht Club Port Bourgas, Bourgas, Bulgaria. Minute Contents 1. WELCOME AND REPORT OF THE PRESIDENT 2 2. REPORT OF THE AD-HOC COMMITTEE 2 3. MINUTES OF THE 2017 GENERAL ASSEMBLY 3 4. MANAGEMENT REPORTS (a) President's Report 3 (b) Technical Committee Chairman Report 3 (c) Promotional and Development Report 3 (d) Class Administration Report 4 (e) Treasurer's Report 4 (f) Auditor's Report 4 (g) Approval of Management Committee Activities 4 5. HONORARY MEMBERSHIP 4 6. PLANS FOR COMING YEARS (a) Financial Issues 5 (b) 2018 Budget 5 (c) Technical Issues 5 (d) Submissions 5 (e) Development Issues 6 (f) Sport Issues 6 7. ANY OTHER BUSINESS 8 Supporting Papers All papers are available to NCAs on request: Item 4(a) - Report of the President Item 4(b) - Report of the Technical Committee Chairman Item 4(c) - Report of Promotion and Development Item 5(e) - Treasurer’s Report Item 6(d) - Submissions 01-18, 02-18 Note: The meeting was scheduled for 1730 hours local time on Saturday 19 May 2018 and commenced at 1755 hours. 470 INTERNATIONALE DRAFT Minutes Delegates in Attendance - 470 National Class Association (NCA) representatives Argentina Gonzalo Heredia Italy Gabrio Zandona Austria Lukas Mahr Japan Proxy to BUL Bulgaria Yana Vasileva Poland Zdzislaw Staniul Croatia Goran Martinovic Romania Dan Mitici Finland Proxy to SWE Russia Michail Zabolotnov France Camille Hautefaye Slovenia -

2019 Handbook
International Laser Class Association © Sailing Energy / World Sailing © Sailing Energy / World 2019 Handbook Constitution and Class Rules BUSINESS OFFICE International Laser Class Association, PO Box 49250, Austin, Texas, 78765, USA Tel: +1-512-270-6727 Email: [email protected] Website: www.laserinternational.org www.facebook.com/intlaserclass Twitter: ILCA@intlaserclass REGIONAL OFFICES ASIA NORTH AMERICA Aileen Loo One Design Management, 2812 Canon Street, Email: ladyhelm@hotmail .com San Diego, CA 92106, USA Tel: +1 619 222 0252 Fax: +1 619 222 0528 EUROPE Email: sherri@odmsail .com Societe Nautique de Genève, Port Noir, Web: www .laser .org CH-1223 Cologny, Suisse North American Exec . Director: Sherri Campbell Email: entryeurilca@gmail .com Web: www .eurilca .org OCEANIA Chairman: Jean-Luc Michon 118 The Promenade, Camp Hill, CENTRAL AND SOUTH AMERICA 4152 Queensland, Australia Tel: +61 404 17644086 San Lorenzo 315 Piso 13, La Lucila, Email: kenhurling@hotmail .com (c .p .1636) Buenos Aires, Argentina Web: laserasiapacific .com Tel: +54 11 4799 1285 Mob: +54 911 4445 Chairman: Ken Hurling 4253 Email: cpalombo@palombohnos .com .ar Central & South American Chair & Executive Secretary: Carlos Palombo ARG WORLD COUNCIL MEMBERS (Full addresses at www.laserinternational.org) President . Tracy Usher USA tracy .usher .ilca@gmail .com Vice President . Hugh Leicester AUS hugh@hydrotechnics .com .au Executive Secretary . Eric Faust USA office@laserinternational .org Past President . Heini Wellmann SUI heini@hmwellmann .ch Central & South American Chair . Carlos Palombo ARG cpalombo@palombohnos .com .ar North American Chair . Andy Roy CAN aroy187740@gmail .com Oceania Chair . Ken Hurling AUS kenhurling@hotmail .com European Chair . Jean-Luc Michon FRA michonjl@hotmail .com Asian Chair . -

Laser Radial Women Final
2020 Laser Radial Women's World Championship – Final Results Melbourne, Australia GOLD FLEET Rank Fleet Sailor Sailor ID Country Sail No Q1 Q2 Q3 Q4 Q5 Q6 F1 F2 F3 F4 Total Net 1 Gold Marit Bouwmeester NEDMB7 NED 6 -3 3 1 1 1 1 1 24 10 -29 74 42 2 Gold Maxime Jonker NEDMJ5 NED 13 (54) UFD 20 3 4 3 3 3 3 -21 5 119 44 3 Gold Line Flem Høst NORLH5 NOR 12 -19 2 5 10 13 1 6 5 3 -43 107 45 4 Gold Anne-Marie Rindom DENAR2 DEN 1 1 3 2 2 -18 10 20 15 4 -38 113 57 5 Gold Magdalena Kwasna POLMK38 POL 29 8 -17 10 2 2 10 2 -17 7 17 92 58 6 Gold Josefin Olsson SWEJO4 SWE 7 -36 7 15 3 1 3 4 12 15 -25 121 60 7 Gold Daphne van der Vaart NEDDV11 NED 19 11 -21 9 6 4 6 27 -36 1 3 124 67 8 Gold Manami Doi JPNMD3 JPN 8 6 4 7 -19 5 7 22 1 -27 15 113 67 9 Gold Emma Plasschaert BELPE1 BEL 3 -9 2 3 1 3 8 -30 25 9 18 108 69 10 Gold Mirthe Akkerman NEDMA3 NED 37 4 9 (54) RET 10 11 14 9 -35 12 2 160 71 11 Gold Vasileia Karachaliou GREVK5 GRE 5 2 6 -14 11 4 12 8 32 -49 6 144 81 12 Gold Annalise Murphy IRLAM24 IRL 78 -38 9 1 9 7 2 (54) UFD 2 2 54 RET 178 86 13 Gold Svenja Weger GERSW22 GER 20 3 26 10 5 -31 12 7 16 8 -28 146 87 14 Gold Paige Railey USAPR8 USA 11 -27 4 23 7 9 6 -34 11 23 9 153 92 15 Gold Marie Bolou FRAMB29 FRA 38 4 8 -15 15 7 13 -40 9 25 11 147 92 16 Gold Maud Jayet SUIMJ3 SUI 10 2 1 6 12 -17 8 32 -38 13 20 149 94 17 Gold Alison Young GBRAY5 GBR 2 -21 6 4 4 2 5 19 -33 22 33 149 95 18 Gold Mara Stransky AUSMS65 AUS 26 5 -22 8 5 14 5 -44 20 28 10 161 95 19 Gold Tuula Tenkanen FINTT1 FIN 9 -37 1 9 12 14 4 33 19 5 -49 183 97 20 Gold Marie Barrue FRAMB65 -

2016 Nacra 17, 49Er & 49Erfx World Championship
2016 Nacra 17, 49er & 49erFX World Championship manage2sail Página 1 de 12 manage2sail.com 2016 Nacra 17, 49er & 49erFX World Championship Results 49er Scoring System : Low Point Preliminary results Rating System : One Design Published : 2/15/2016 4:10:24 PM Discard(s) after race : Opening Series - 4; Final Series - 4; Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 F10 F11 F12 F13 F14 F15 M 16 Nr Sail Number Team Club TN 1 NZL 1 Peter BURLING Tauranga/… 1.0 1.0 1.0 1.0 1.0 3.0 1.0 2.0 71.0 40.0 Blair TUKE (11.0) 4.0 (20.0) 2.0 2.0 3.0 12.0 6.0 2 AUT 84 Nico Luca Marc DELLE KARTH KYK 10.0 16.0 2.0 1.0 (22.0) 3.0 7.0 1.0 118.0 81.0 Nikolaus Leopold RESCH 7.0 5.0 8.0 5.0 5.0 7.0 (15.0) 4.0 3 GBR 33 Dylan FLETCHER-SCOTT 5.0 10.0 4.0 2.0 7.0 6.0 19.0 (23.0) 123.0 88.0 Alain SIGN 4.0 3.0 9.0 4.0 6.0 (12.0) 7.0 2.0 http://www.manage2sail.com/en -US/event/8845f1dc -a649 -4880 -bf22 -abf02522e09a/ 23/ 02/ 2016 2016 Nacra 17, 49er & 49erFX World Championship manage2sail Página 2 de 12 Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 F10 F11 F12 F13 F14 F15 M 16 Nr Sail Number Team Club TN 4 POL 52 Tomasz JANUSZEWSKI 3.0 4.0 11.0 2.0 20.0 4.0 (24.0) 4.0 138.0 95.0 Jacek NOWAK 2.0 9.0 13.0 (19.0) 7.0 4.0 2.0 10.0 5 DEN 30 Jonas WARRER KDY 1.0 11.0 (14.0) 6.0 5.0 5.0 5.0 14.0 130.0 99.0 Anders THOMSEN 5.0 1.0 7.0 9.0 (17.0) 11.0 5.0 14.0 6 AUS 2 Nathan OUTTERIDGE 15.0 2.0 1.0 3.0 4.0 7.0 (18.0) 6.0 131.0 99.0 Iain JENSEN 1.0 13.0 11.0 (14.0) 4.0 9.0 1.0 22.0 OCS 7 GBR 6 John PINK 2.0 6.0 6.0 5.0 2.0 1.0 (17.0)