ETARA PC Version 3.3 User's Guide Reliability, Availability, Maintainability Simulation Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Appendix E: Booklists and Articles from Truths to Teach, Stories to Tell
Appendix E: Booklists and Articles from Truths to Teach, Stories to Tell Appendix E: Booklists and Articles from Truths to Teach, Stories to Tell 191 Appendix E: Booklists and Articles from Truths to Teach, Stories to Tell 192 Appendix E: Booklists and Articles from Truths to Teach, Stories to Tell Thoughts on Choosing and Using Books with Your Children When Should I Start Reading to My Child? Short Answer: As soon as you want! Reading is simply another form of language, so why not? Most parents begin talking to their children from birth, and children begin absorbing understanding through voice tone even before the words make sense. But, if you begin reading to your young infant, don’t do it with the agenda of getting them to polish off the Bible by the time they are one! (This sounds ridiculous, but it’s amazing what ideas we eager parents get into our heads!) Do it to begin the pattern of enjoying time together, cuddled on your lap, listening to your voice and with an open heart. Gradually, as your child develops, watch for cues that they are ready for more. You will see them begin to point to pictures or bring you particular books to read (usually over and over again!). Then you know they are engaging with not just the feel of reading, but the content of what you are reading. That’s when you can begin to really think about using books to fi ll their hearts and minds with truth. Bible Storybooks FAQs #1: What’s the diff erence between a Bible storybook and a full Bible? Which would you recommend to using? A Bible storybook is a collection of Bible stories, written by an author, while the Bible is...well....the Bible--a translation of the entire Old Testament and New Testament into a particular language by a group of Bible scholars. -

アーティスト 商品名 品番 ジャンル名 定価 URL 100% (Korea) RE
アーティスト 商品名 品番 ジャンル名 定価 URL 100% (Korea) RE:tro: 6th Mini Album (HIP Ver.)(KOR) 1072528598 K-POP 2,290 https://tower.jp/item/4875651 100% (Korea) RE:tro: 6th Mini Album (NEW Ver.)(KOR) 1072528759 K-POP 2,290 https://tower.jp/item/4875653 100% (Korea) 28℃ <通常盤C> OKCK05028 K-POP 1,296 https://tower.jp/item/4825257 100% (Korea) 28℃ <通常盤B> OKCK05027 K-POP 1,296 https://tower.jp/item/4825256 100% (Korea) 28℃ <ユニット別ジャケット盤B> OKCK05030 K-POP 648 https://tower.jp/item/4825260 100% (Korea) 28℃ <ユニット別ジャケット盤A> OKCK05029 K-POP 648 https://tower.jp/item/4825259 100% (Korea) How to cry (Type-A) <通常盤> TS1P5002 K-POP 1,204 https://tower.jp/item/4415939 100% (Korea) How to cry (Type-B) <通常盤> TS1P5003 K-POP 1,204 https://tower.jp/item/4415954 100% (Korea) How to cry (ミヌ盤) <初回限定盤>(LTD) TS1P5005 K-POP 602 https://tower.jp/item/4415958 100% (Korea) How to cry (ロクヒョン盤) <初回限定盤>(LTD) TS1P5006 K-POP 602 https://tower.jp/item/4415970 100% (Korea) How to cry (ジョンファン盤) <初回限定盤>(LTD) TS1P5007 K-POP 602 https://tower.jp/item/4415972 100% (Korea) How to cry (チャンヨン盤) <初回限定盤>(LTD) TS1P5008 K-POP 602 https://tower.jp/item/4415974 100% (Korea) How to cry (ヒョクジン盤) <初回限定盤>(LTD) TS1P5009 K-POP 602 https://tower.jp/item/4415976 100% (Korea) Song for you (A) OKCK5011 K-POP 1,204 https://tower.jp/item/4655024 100% (Korea) Song for you (B) OKCK5012 K-POP 1,204 https://tower.jp/item/4655026 100% (Korea) Song for you (C) OKCK5013 K-POP 1,204 https://tower.jp/item/4655027 100% (Korea) Song for you メンバー別ジャケット盤 (ロクヒョン)(LTD) OKCK5015 K-POP 602 https://tower.jp/item/4655029 100% (Korea) -
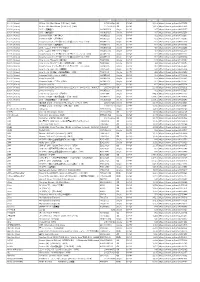
URL 100% (Korea)
アーティスト 商品名 オーダー品番 フォーマッ ジャンル名 定価(税抜) URL 100% (Korea) RE:tro: 6th Mini Album (HIP Ver.)(KOR) 1072528598 CD K-POP 1,603 https://tower.jp/item/4875651 100% (Korea) RE:tro: 6th Mini Album (NEW Ver.)(KOR) 1072528759 CD K-POP 1,603 https://tower.jp/item/4875653 100% (Korea) 28℃ <通常盤C> OKCK05028 Single K-POP 907 https://tower.jp/item/4825257 100% (Korea) 28℃ <通常盤B> OKCK05027 Single K-POP 907 https://tower.jp/item/4825256 100% (Korea) Summer Night <通常盤C> OKCK5022 Single K-POP 602 https://tower.jp/item/4732096 100% (Korea) Summer Night <通常盤B> OKCK5021 Single K-POP 602 https://tower.jp/item/4732095 100% (Korea) Song for you メンバー別ジャケット盤 (チャンヨン)(LTD) OKCK5017 Single K-POP 301 https://tower.jp/item/4655033 100% (Korea) Summer Night <通常盤A> OKCK5020 Single K-POP 602 https://tower.jp/item/4732093 100% (Korea) 28℃ <ユニット別ジャケット盤A> OKCK05029 Single K-POP 454 https://tower.jp/item/4825259 100% (Korea) 28℃ <ユニット別ジャケット盤B> OKCK05030 Single K-POP 454 https://tower.jp/item/4825260 100% (Korea) Song for you メンバー別ジャケット盤 (ジョンファン)(LTD) OKCK5016 Single K-POP 301 https://tower.jp/item/4655032 100% (Korea) Song for you メンバー別ジャケット盤 (ヒョクジン)(LTD) OKCK5018 Single K-POP 301 https://tower.jp/item/4655034 100% (Korea) How to cry (Type-A) <通常盤> TS1P5002 Single K-POP 843 https://tower.jp/item/4415939 100% (Korea) How to cry (ヒョクジン盤) <初回限定盤>(LTD) TS1P5009 Single K-POP 421 https://tower.jp/item/4415976 100% (Korea) Song for you メンバー別ジャケット盤 (ロクヒョン)(LTD) OKCK5015 Single K-POP 301 https://tower.jp/item/4655029 100% (Korea) How to cry (Type-B) <通常盤> TS1P5003 Single K-POP 843 https://tower.jp/item/4415954 -

Download Bigbang Made Full Album Japanese K2nblog Zinnia Magenta
download bigbang made full album japanese k2nblog Zinnia Magenta. Download Musik, MV/PV Jepang & Korea Full Version + Drama Korea Subtittle Indonesia. Newest Post. Download [Album] BIGBANG - MADE. BIGBANG – MADE [FULL ALBUM] Release Date: 2016.12.13 Genre: Rap / Hip-hop, Ballad, Dance, Folk, Rock Language: Korean Bit Rate: MP3-320kbps + iTunes Plus AAC M4A Big Bang’s tenth anniversary project comes to an end with the last album of the Made series. Besides the Made singles, such as Bang Bang Bang, Loser, Bae Bae and “Let’s Not Fall in Love,” the album also features three new tracks, namely the double title numbers FXXK IT and Last Dance, as well as Girlfriend written by G-Dragon, TOP and YG in-house producer Teddy. Track List: 01. 에라 모르겠다 (FXXK IT) *Title 02. LAST DANCE *Title 03. GIRLFRIEND 04. 우리 사랑하지 말아요 (LET’S NOT FALL IN LOVE) 05. LOSER 06. BAE BAE 07. 뱅뱅뱅 (BANG BANG BANG) 08. 맨정신 (SOBER) 09. IF YOU 10. 쩔어 (ZUTTER) (GD & T.O.P) 11. WE LIKE 2 PARTY. Download Album File: BIGBANG – MADE [Zinnia Magenta].rar Size: 95.9 MB. Download bigbang made full album japanese k2nblog. BIG BANG Albums Download. BIGBANG – Alive (Monster Edition) 1. Still Alive 2. MONSTER 3. FANTASTIC BABY 4. Blue 5. Love Dust 6. FEELING 7. Ain't No Fun 8. BAD BOY 9. EGO 10. Wings 11. Bingle Bingle 12. Haru Haru (Japanese ver.) DOWNLOAD. BIGBANG - Still Alive Special Edition. 1. Still Alive 2. MONSTER 3. Feeling 4. FANTASTIC BABY 5. BAD BOY 6. Blue 7. Round and Round 빙글빙글 (Bingeul Bingeul) 8. -

373-222 FM Chap 21.Qxd
READY-TO-INSTALL PRODUCTS RESIDENTIAL APPLICATIONS Installing a Corian® Ready-To-Install One-Piece Vanity Top & Bowl Corian® One-Piece Vanity Tops & Bowls are ready to install and require only cabinet or bracket support plus drilling of the faucet holes, as per plumbing requirements. The One-Piece Vanity Top & Bowl can be used for residential and commercial applications. Residential applications usually only require cabinet support, while commercial applications often require additional support as well. The front skirt needs to be fitted prior to installation. 21.1 Preparation RESIDENTIAL Inspect installation area and make sure cabinet is secured properly. Unpack APPLICATIONS vanity and check for shipping damage. (Report any problems to your place of purchase before proceeding further with installation.) Note: Follow all manufacturer’s instructions and safety information on silicone caulk containers. Ensure adequate ventilation before applying. Installation 1. Trial-fit vanity top to cabinet and wall. Use a utility knife to cut away interfering drywall as required. If vanity top “rocks,” insert a shim beneath “lugs” on underside of vanity top until it is level. Remove vanity top and secure shims to vanity cabinet. 1 2. If vanity top does not have predrilled faucet holes, drill holes using a 1 /4” (31 mm) diameter hole saw bit and paper pattern that comes with faucet hardware (Figure 21.1.A). If you need another paper pattern, determine if faucet hardware has 4” (102 mm) or 8” (203 mm) centers. Then use the appropriate size pattern found at the end of this instruction booklet. Note: Before drilling, be sure faucet hardware will fit in recessed faucet deck area. -

Assisted Living | Calendar of Events
August 2020 | Assisted Living | Calendar of Events Adult Living For Those Who Seek More. Sun Mon Tue Wed Thu Fri Sat Visiting Physicians: Visiting Physicians: Salon Services: Dr. Belford—Psychiatrist Dr. Ali—Primary Care Physician Manicures 1st Thursday of every month | Wednesdays | 8a —12:00p (WC) Currently unavailable Riverside Senior Life Communities 9a—12:00p partners with residents & their families to identify their desires & dreams, Hair Appointments Ashley Chappell— & work together to bring those needs, passions, & abilities to life. We focus on the Available in the salon Dr. Ralley—Podiatrist Advanced Practice Nurse Dimensions of Wellness to assure our residents are provided a well-rounded array of 85 E. Burn Road Mondays: 9:00a—12:00p Wednesday, August 26th (WC) Thursdays | 9a -12:00p (WC) programing. People at every age and stage of ability seek opportunities to remain productive, Bourbonnais, IL 60914 Tuesdays: 9:00a—4:00p 815-935-3332 Wednesdays: 1:00p—4:00p contributing members of a community. They search for ways to stay mentally and physically Jana Whalen—Audiologist independent and active; they seek resources to meet their spiritual needs; and they want to keep August 28th | 9a -10:00p (WC) Contact the Concierge to sign up expanding their knowledge. In addition to what you see on this calendar there are many small group To schedule a single or for any Outings or Special Events Banking Services: programs occurring as well as one-on-one opportunities to assure all of our residents are engaged. reoccurring appointment, First Trust Bank If you have a suggestion for something your loved one may enjoy, please contact the Concierge. -

Creation Science Catalog
R e s o u r c e M a t e r i a l Creation Association of British Columbia PO Box 39577 RPO White Rock Surrey, BC V4A 0A9 (604) 535-0019 www.creationbc.org 2020-2021 Cover Design by Victoria Rowbottom ORDER FORM ON PAGE 27 A is for Adam (spiral) Ken and Mally Ham Brilliant CHILDREN’S BOOKS Creation Story for Children Helen & David Haidle new illustrations enhance rhymes and learning exer- Filled with vibrant images of God’s creation week, this cises within a spiral-bound easel book format to make Also suitable for book will help children grasp the greatness of God. teaching much easier. This innovative book contains $14.00 tips on presenting kid-sized nuggets of biblical informa- Christian education tion. $14.00 Dinky Dinosaur: Creation Days Darrell Wiskur For preschoolers, the cartoon dinosaur Dinky tells about Ken Ham A rhyming account that A Special Door each day of creation in this full-colour board book. highlights the link between Noah’s flood and the $6.00 powerful need for a personal Saviour in Jesus Christ. $14.00 Dinosaur Activity Book Earl & Bonita A.P. Advanced Readers Series This is a step Snellenberger Kids will enjoy learning about some of up from the Early Reader series aimed at chil- the most popular – and most unusual – dinosaurs in dren in grades 2 & 3. Amazing Beauty/Amazing this book chockfull of information. The book includes Copies of God’s Design/Amazing Dinosaurs/ mazes, puzzles, word finds, games and other skill chal- Amazing Human Body/Amazing Migrating lenges. -

No. Title Artist 1 2014 2NE1 WORLD TOUR LIVE-ALL OR NOTHING in SEOUL 2NE1 2 CRUSH (WHITE) 2NE1 3 CRUSH (BLACK) 2NE1 4 LEGEND OF
9:;<:=>?@ABD EFG;HIDBDJDA SCB EASY ZAAP ON SALE K9LEDML! P:AEFG 23-24 Q:APDB> 2017 EFG K:=A 5 Paragon Hall, Siam Paragon No. Title Artist 1 2014 2NE1 WORLD TOUR LIVE-ALL OR NOTHING IN SEOUL 2NE1 2 CRUSH (WHITE) 2NE1 3 CRUSH (BLACK) 2NE1 4 LEGEND OF 2PM 2PM 5 GIVE ME LOVE 2PM 6 NO.5 THAILAND EDITION 2PM 7 2PM OF 2PM STANDARD VERSION 2PM 8 ONE DAY 2PM+2AM 'ONE DAY' 9 AAA 10TH ANNIVERSARY BEST AAA 10 MADE SERIES ?M’ WHITE BIGBANG 11 MADE SERIES ?A’ WHITE BIGBANG 12 SUNRISE THAILAND EDITION DAY6 13 THE DAY DAY6 14 DAYDDREAM THAILAND EDITION DAY6 15 SHOEBOX EPIK HIGH 16 COUP D'ETAT (BLACK) G-DRAGON 17 COUP D'ETAT (RED) G-DRAGON 18 G-DRAGON'S COLLECTION ONE OF A KIND G-DRAGON 19 FIRST MINI ALBUM ONE OF A KIND (GOLD) G-DRAGON 20 FLIGHT LOG:ARRIVAL THAILAND EDITION GOT7 21 JUST RIGHT THAILAND EDITION GOT7 22 FLIGHT LOG: DEPARTURE THAILAND EDITON GOT7 23 MAD THAILAND EDITION GOT7 24 FLIGHT LOG:TURBULENCE GOT7 25 MY SWAGGER GOT7 26 1ST&2ND MINI ALBUM:THAILAND SPECIAL SET GOT7 27 MORIAGATTEYO GOT7 28 COLORS THAILAND EDITION MISS A 29 RISE TAEYANG 30 TWICECOASTER:LANE2 THAILAND EDITION TWICE 31 PAGE TWO THAILAND EDITION TWICE 32 FATE NUMBER FOR WINNER 33 WE ARE X SOUNDTRACK X JAPAN 34 DIVISION THE GAZETTE 35 BEST ALBUM SCANDAL 36 ENCORE SHOW SCANDAL 37 YELLOW SCANDAL 38 HELLO WORLD SCANDAL 39 OSAKA-JO HALL 2013 WONDERFUL TONIGHT SCANDAL 40 STANDARD SCANDAL 41 DEPARTURE SCANDAL 42 WORLD TOUR 2012 LIVE AT MADISON SQUARE GARDEN L'ARC-EN-CIEL 43 LIVE 2014 AT KOKURITSU KYOUGIJYOU L'ARC-EN-CIEL 44 OVER THE L'ARC-EN-CIEL DOCUMENTARY FILMS WORLD TOUR L'ARC-EN-CIEL2012 -

UNIVERSAL MUSIC • American Authors – Oh What a Life • Dierks
American Authors – Oh What A Life Dierks Bentley – Riser David Nail – I’m A Fire New Releases From Fontana North Inside!!! And more… UNI14-08 “Our assets on-line” UNIVERSAL MUSIC 2450 Victoria Park Ave., Suite 1, Willowdale, Ontario M2J 5H3 Phone: (416) 718.4000 Artwork shown may not be final UNIVERSAL MUSIC CANADA NEW RELEASE Artist/Title: BECK – MORNING PHASE Bar Code: Cat. #: B001983802 Price Code: SP Order Due: Feb 13, 2014 Release Date: Feb 25, 2014 02537 64975 6 4 File: Alternative Genre Code: 2 Box Lot: 25 Key Tracks: Blue Moon Waking Light Super Short Sell Cycle Artist/Title: BECK – MORNING PHASE (Vinyl) – vinyl is one way sale Bar Code: Cat. #: B001983901 Price Code: Q 02537 64974 Order Due: Feb 13, 2014 Release Date: Feb 25, 2014 6 7 File: Alternative Genre Code: 2 Box Lot: Beck has signed to Capitol Records, and will release ‘Morning Phase’, the first album of all new material since 2008's universally acclaimed Modern Guilt on February 25th 2014. The new record has been described as a companion piece of sorts to Beck's 2002 classic Sea Change. Featuring many of the same musicians who played on that record, Morning Phase harkens back to the stunning harmonies, song craft and staggering emotional impact of Sea Change, while surging forward with infectious optimism. Morning Phase will be released on CD, vinyl, and digital download. BUY HERE’s WHY: -Beck has a >2x Platinum sales base in Canada, his first album of new material in 6 years. -Massive press looks being secured around release. -

Summer Reading for Rising Fifth Grade 2021
St. Michael’s Episcopal School Summer 2020 Reading List for Rising Fifth Grade Summer Reading Requirement The Liberation of Gabriel King by K.L. Going ACTION ADVENTURE Bell, P.G. The Train to Impossible Places (series) Bosch, Pseudonymous, Bosch The Name of This Book is Secret (series) Burt, Jake Greetings from Witness Protection Chandler, Matt Alcatraz: a chilling interactive adventure (series) Cowell, Cressida The Wizards of Once (series) Creech, Sharon The Wanderer * Gibbs, Stuart Charlie Thorne and the Last Equation Ginns, Russell Samantha Spinner and the Super Secret Plans (series) Haddix, Margaret Peterson The Strangers (series) Hashimoto, Meika The Trail Hiassen, Carl Hoot*; Flush; Scat; Chomp Mass, Wendy The Candymakers (series) Patterson, James Treasure Hunters (series) Ponti, James City Spies Potter, Ellen The Kneebone Boy Riordan, Rick The Lost Hero (series); The Sword of Summer ( Magnus Chase series) Rylander, Chris Fourth Stall (series); The Legend of Greg (series) Smith, Roland Independence Hall (series) White, Wade Albert The Adventurer’s Guide to Successful Escapes (series) BONE RATTLERS Arden, Katherine Small Spaces, Dead Voices Black, Holly Doll Bones DeFelice Cynthia, The Ghost of Fossil Glen Grabenstein, Chris The Crossroads Hahn, Mary Downing The Old Willis Place: a ghost story; The Ghost of Crutchfield Hall Scieszka, Jon Terrifying Tales; Thriller COOL CLASSICS Armstrong, William H. Sounder* Juster, Norton The Phantom Tollbooth Konigsburg, E. L. From the Mixed-up Files of Mrs. Basil E. Frankweiler* L’Engle, Madeleine A Wrinkle in Time* Lewis, C.S. The Lion, the Witch, and the Wardrobe Paterson, Katherine Bridge to Terabithia* FLY WITH FANTASY Applegate, Katherine Crenshaw; The Last (Endling, Book 1) (series); The One and Only Ivan*; The One and Only Bob; Wishtree Barnhill, Kelly R. -

Big Bang E Mp3, Flac, Wma
Big Bang e mp3, flac, wma DOWNLOAD LINKS (Clickable) Genre: Electronic / Hip hop / Pop Album: e Country: South Korea Released: 2015 Style: Pop Rap, Dance-pop, K-pop MP3 version RAR size: 1909 mb FLAC version RAR size: 1233 mb WMA version RAR size: 1661 mb Rating: 4.4 Votes: 638 Other Formats: ASF WAV APE DMF MP2 XM AHX Tracklist 1 –Big Bang 우리 사랑하지 말아요 Let's Not Fall In Love 2 –GD* & T.O.P 쩔어 Zutter 3 –Big Bang Bang Bang Bang 4 –Big Bang 맨정신 Sober 5 –Big Bang If You 6 –Big Bang Loser 7 –Big Bang Bae Bae 8 –Big Bang We Like 2 Party 9 –Big Bang 우리 사랑하지 말아요 Let's Not Fall In Love (Inst.) 10 –GD* & T.O.P 쩔어 Zutter (Inst.) Companies, etc. Distributed By – KT Music Co., Ltd. Notes 2 versions. E or e version. Incudes: - 24-page booklet - 1 Random photocard (out of 6) - 1 Random puzzle ticket - Poster - Clip book (Limited pre-order gift) Barcode and Other Identifiers Barcode: 8809269505088 Other versions Category Artist Title (Format) Label Category Country Year YGK 0555 Big Bang E (CD, EP, Bla) YG Entertainment YGK 0555 South Korea 2015 [YG Music] E (6xFile, AAC, none Big Bang YG Entertainment none 2015 EP, 256) none Big Bang E (2xFile, AAC, Single, 256) YG Entertainment none 2015 Made Series [E] (2xFile, none Big Bang Avex Entertainment none 2015 AAC, Single, 256) Related Music albums to e by Big Bang 1. Benny Barbara et les "Los Latins Soul" - BANG BANG 2. Big Bang - D 3. -
Revised Uniform Limited Liability Company Act
BUSINESS LAW SECTION PARTNERSHIPS AND LIMITED LIABILITY COMPANIES COMMITTEE THE STATE BAR OF CALIFORNIA 180 Howard Street San Francisco, CA 94105-1639 http://www.calbar.org/buslaw/ REVISED UNIFORM LIMITED LIABILITY COMPANY ACT LEGISLATIVE PROPOSAL (BLS-2011-06) TO: Office of Governmental Affairs FROM: Ron Wargo, Chair Business Law Section (the “Section”) Partnerships and Limited Liability Companies Committee (the “Committee”) DATE: June 1, 2010 RE: Proposal to adopt Revised Uniform Limited Liability Company Act and repeal the Beverly-Killea Limited Liability Company Act SECTION ACTION AND CONTACTS Date of Approval by Section Executive Committee (the “Executive Committee”): July 16, 2010 Approval Vote: For: 15 Against: 0 Executive Committee Contact: Committee Contact: Stewart L. McDowell Phil Jelsma Vice Chair for Legislation Vice Chair Gibson Dunn & Crutcher c/o Luce Forward 1 Montgomery Street 600 West Broadway Suite 2600 San Francisco, CA 94104 San Diego, CA 92101 Tel: 415-393-8322 Tel: 619-699-2565 [email protected] [email protected] 1 HISTORY, DIGEST AND PURPOSE This Proposal seeks to adopt the National Conference of Commissioners on Uniform State Laws’ (“NCCUSL”) Revised Uniform Limited Liability Company Act (“RULLCA”) with certain modifications under California law. Idaho, Iowa, Nebraska and Wyoming have already adopted RULLCA. The District of Columbia has introduced RULLCA. Next year it is anticipated that Alabama, Arkansas, Minnesota, Montana, New Jersey, South Carolina and the Virgin Islands will introduce RULLCA. History The Beverly-Killea Limited Liability Company Act became effective in 1994. Some of the code sections affected by this Proposal have been amended since their original codification. Our Committee was involved with certain technical corrections included in SB 141 which was chaptered in 1996 (Chap.