Proof of CMB-Driven X-Ray Brightening of High-Z Radio Galaxies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

NASA's Goddard Space Flight Center Laboratory for High Energy
1 NASA’s Goddard Space Flight Center Laboratory for High Energy Astrophysics Greenbelt, Maryland 20771 @S0002-7537~99!00301-7# This report covers the period from July 1, 1997 to June 30, Toshiaki Takeshima, Jane Turner, Ken Watanabe, Laura 1998. Whitlock, and Tahir Yaqoob. This Laboratory’s scientific research is directed toward The following investigators are University of Maryland experimental and theoretical research in the areas of X-ray, Scientists: Drs. Keith Arnaud, Manuel Bautista, Wan Chen, gamma-ray, and cosmic-ray astrophysics. The range of inter- Fred Finkbeiner, Keith Gendreau, Una Hwang, Michael Loe- ests of the scientists includes the Sun and the solar system, wenstein, Greg Madejski, F. Scott Porter, Ian Richardson, stellar objects, binary systems, neutron stars, black holes, the Caleb Scharf, Michael Stark, and Azita Valinia. interstellar medium, normal and active galaxies, galaxy clus- Visiting scientists from other institutions: Drs. Vadim ters, cosmic-ray particles, and the extragalactic background Arefiev ~IKI!, Hilary Cane ~U. Tasmania!, Peter Gonthier radiation. Scientists and engineers in the Laboratory also ~Hope College!, Thomas Hams ~U. Seigen!, Donald Kniffen serve the scientific community, including project support ~Hampden-Sydney College!, Benzion Kozlovsky ~U. Tel such as acting as project scientists and providing technical Aviv!, Richard Kroeger ~NRL!, Hideyo Kunieda ~Nagoya assistance to various space missions. Also at any one time, U.!, Eugene Loh ~U. Utah!, Masaki Mori ~Miyagi U.!, Rob- there are typically between twelve and eighteen graduate stu- ert Nemiroff ~Mich. Tech. U.!, Hagai Netzer ~U. Tel Aviv!, dents involved in Ph.D. research work in this Laboratory. Yasushi Ogasaka ~JSPS!, Lev Titarchuk ~George Mason U.!, Currently these are graduate students from Catholic U., Stan- Alan Tylka ~NRL!, Robert Warwick ~U. -

Earth and Space Science. a Guide for Secondary Teachers. INSTITUTION Pennsylvania State Dept
DOCUMENT RESUME ED 094 956 SE 016 611 AUTHOR Bolles, William H.; And Others TITLE Earth and Space Science. A Guide for Secondary Teachers. INSTITUTION Pennsylvania State Dept. of Education, Harrisburg. Bureau of Curriculum Services. PUB DATE 73 NOTE 200p. EDRS PRICE MF-$O.75 HC-$9.00 PLUS POSTAGE DESCRIPTORS Aerospace Education; *Astronomy; *Curriculum Guides; *Earth Science; Geology; Laboratory Experiments; Oceanology; Science Activities; Science Education; *Secondary School Science IDENTIFIERS Pennsylvania ABSTRACT Designed for use in Pennsylvania secondary school science classes, this guide is intended to provide fundamental information in each of the various disciplines of the earth sciences. Some of the material contained in the guide is intended as background material for teachers. Five units are presented: The Earth, The Oceans, The Space Environment, The Atmosphere, and The Exploration of Space. The course is organized so that students proceed from the familiar, everyday world to the atmosphere and the space environment. Teaching geology in the fall takes advantage of weather conditions which permit field study. The purpose of the Earth and Space Science course is to encourage student behaviors which will be indicative of a broad understanding of man1s physical environment of earth and space as well as an awareness of the consequences which could result from changes which man may effect.(PEB) BEST COPY AVAILABLE U S DEPARTMENT OF HEALTH. EDUCATION & WELFARE NATIONAL INSTITUTE OF 6 Fe elz+C EDUCATION Try,' DOCUMENT FIRSBEEN REPRO -

Astrophysics
Publications of the Astronomical Institute rais-mf—ii«o of the Czechoslovak Academy of Sciences Publication No. 70 EUROPEAN REGIONAL ASTRONOMY MEETING OF THE IA U Praha, Czechoslovakia August 24-29, 1987 ASTROPHYSICS Edited by PETR HARMANEC Proceedings, Vol. 1987 Publications of the Astronomical Institute of the Czechoslovak Academy of Sciences Publication No. 70 EUROPEAN REGIONAL ASTRONOMY MEETING OF THE I A U 10 Praha, Czechoslovakia August 24-29, 1987 ASTROPHYSICS Edited by PETR HARMANEC Proceedings, Vol. 5 1 987 CHIEF EDITOR OF THE PROCEEDINGS: LUBOS PEREK Astronomical Institute of the Czechoslovak Academy of Sciences 251 65 Ondrejov, Czechoslovakia TABLE OF CONTENTS Preface HI Invited discourse 3.-C. Pecker: Fran Tycho Brahe to Prague 1987: The Ever Changing Universe 3 lorlishdp on rapid variability of single, binary and Multiple stars A. Baglln: Time Scales and Physical Processes Involved (Review Paper) 13 Part 1 : Early-type stars P. Koubsfty: Evidence of Rapid Variability in Early-Type Stars (Review Paper) 25 NSV. Filtertdn, D.B. Gies, C.T. Bolton: The Incidence cf Absorption Line Profile Variability Among 33 the 0 Stars (Contributed Paper) R.K. Prinja, I.D. Howarth: Variability In the Stellar Wind of 68 Cygni - Not "Shells" or "Puffs", 39 but Streams (Contributed Paper) H. Hubert, B. Dagostlnoz, A.M. Hubert, M. Floquet: Short-Time Scale Variability In Some Be Stars 45 (Contributed Paper) G. talker, S. Yang, C. McDowall, G. Fahlman: Analysis of Nonradial Oscillations of Rapidly Rotating 49 Delta Scuti Stars (Contributed Paper) C. Sterken: The Variability of the Runaway Star S3 Arietis (Contributed Paper) S3 C. Blanco, A. -

Starry Nights Typeset
Index Antares 104,106-107 Anubis 28 Apollo 53,119,130,136 21-centimeter radiation 206 apparent magnitude 7,156-157,177,223 57 Cygni 140 Aquarius 146,160-161,164 61 Cygni 139,142 Aquila 128,131,146-149 3C 9 (quasar) 180 Arcas 78 3C 48 (quasar) 90 Archer 119 3C 273 (quasar) 89-90 arctic circle 103,175,212 absorption spectrum 25 Arcturus 17,79,93-96,98-100 Acadia 78 Ariadne 101 Achernar 67-68,162,217 Aries 167,183,196,217 Acubens (star in Cancer) 39 Arrow 149 Adhara (star in Canis Major) 22,67 Ascella (star in Sagittarius) 120 Aesculapius 115 asterisms 130 Age of Aquarius 161 astrology 161,196 age of clusters 186 Atlantis 140 age of stars 114 Atlas 14 Age of the Fish 196 Auriga 17 Al Rischa (star in Pisces) 196 autumnal equinox 174,223 Al Tarf (star in Cancer) 39 azimuth 171,223 Al- (prefix in star names) 4 Bacchus 101 Albireo (star in Cygnus) 144 Barnard’s Star 64-65,116 Alcmene 52,112 Barnard, E. 116 Alcor (star in Big Dipper) 14,78,82 barred spiral galaxies 179 Alcyone (star in Pleiades) 14 Bayer, Johan 125 Aldebaran 11,15,22,24 Becvar, A. 221 Alderamin (star in Cepheus) 154 Beehive (M 44) 42-43,45,50 Alexandria 7 Bellatrix (star in Orion) 9,107 Alfirk (star in Cepheus) 154 Algedi (star in Capricornus) 159 Berenice 70 Algeiba (star in Leo) 59,61 Bessel, Friedrich W. 27,142 Algenib (star in Pegasus) 167 Beta Cassiopeia 169 Algol (star in Perseus) 204-205,210 Beta Centauri 162,176 Alhena (star in Gemini) 32 Beta Crucis 162 Alioth (star in Big Dipper) 78 Beta Lyrae 132-133 Alkaid (star in Big Dipper) 78,80 Betelgeuse 10,22,24 Almagest 39 big -

Appendix II. Publications
Appendix II. Publications Gemini Staff Publications Papers in PeerReviewed Journals: Bauer, Amanda[4]. A young, dusty, compact radio source within a Lyα halo. Monthly Notices of the Royal Astronomical Society, 389:792-798. September, 2008. Trancho, G.[4]. The early expansion of cluster cores. Monthly Notices of the Royal Astronomical Society, 389:223-230. September, 2008. Stephens, A. W.[11]. Massive stars exploding in a He-rich circumstellar medium - III. SN 2006jc: infrared echoes from new and old dust in the progenitor CSM. Monthly Notices of the Royal Astronomical Society, 389:141-155. September, 2008. Serio, Andrew W.[1]. The variation of Io's auroral footprint brightness with the location of Io in the plasma torus. Icarus, 197:368-374. September, 2008. Radomski, James T.[5]. Understanding the 8 µm versus Paα Relationship on Subarcsecond Scales in Luminous Infrared Galaxies. The Astrophysical Journal, 685:211-224. September, 2008. Volk, K.[47]. Spitzer Survey of the Large Magellanic Cloud, Surveying the Agents of a Galaxy's Evolution (sage). IV. Dust Properties in the Interstellar Medium. The Astronomical Journal, 136:919-945. September, 2008. Díaz, R. J.[3]. Discovery of a [WO] central star in the planetary nebula Th 2-A. Astronomy and Astrophysics, 488:245-247. September, 2008. Schiavon, Ricardo P.[2]. Measuring Ages and Elemental Abundances from Unresolved Stellar Populations: Fe, Mg, C, N, and Ca. The Astrophysical Journal Supplement Series, 177:446- 464. August, 2008. Song, Inseok[3]. Gas and Dust Associated with the Strange, Isolated Star BP Piscium. The Astrophysical Journal, 683:1085-1103. August, 2008. Roth, Katherine C.[22]. -

Probing the Nuclear Obscuration in Radio-Galaxies with Near Infrared Imaging�,��,�
A&A 433, 841–854 (2005) Astronomy DOI: 10.1051/0004-6361:20042072 & c ESO 2005 Astrophysics Probing the nuclear obscuration in radio-galaxies with near infrared imaging,, D. Marchesini1,†, A. Capetti2, and A. Celotti1 1 SISSA/ISAS, via Beirut 2-4, 34014 Trieste, Italy e-mail: [email protected] 2 INAF – Osservatorio Astronomico di Torino, Strada Osservatorio 20, 10025 Pino Torinese, Italy Received 27 September 2004 / Accepted 8 December 2004 Abstract. We present the first near-infrared (K-band) homogeneous observations of a complete sub-sample of the 3CR radio catalogue comprising all High Excitation Galaxies (HEGs) at z < 0.3. After showing that the surface brightness decomposition technique to measure central point-like sources is affected by significant uncertainties for the objects in the studied sample, we present a new, more accurate method based on the R − K color profile. Via this method we find a substantial nuclear K-band excess in all but two HEGs – most likely directly associated with their nuclear emission – and we measure the corresponding 2.12 µm nuclear luminosities. Within the frame-work of the unification scheme for radio-loud active galactic nuclei, it appears that obscuration alone is not able to account for the different nuclear properties of the majority of the HEGs and Broad Line Radio Galaxies (BLRGs), and also scattering of the (optically) hidden nuclear light from a compact region must be invoked. More precisely, for ∼70% of the HEGs the observed point-like optical emission is dominated by the scattered component, while in the K-band both scattered and direct light passing through the torus contribute to the observed nuclear luminosity. -

General Disclaimer One Or More of the Following Statements May Affect
General Disclaimer One or more of the Following Statements may affect this Document This document has been reproduced from the best copy furnished by the organizational source. It is being released in the interest of making available as much information as possible. This document may contain data, which exceeds the sheet parameters. It was furnished in this condition by the organizational source and is the best copy available. This document may contain tone-on-tone or color graphs, charts and/or pictures, which have been reproduced in black and white. This document is paginated as submitted by the original source. Portions of this document are not fully legible due to the historical nature of some of the material. However, it is the best reproduction available from the original submission. Produced by the NASA Scientific and Technical Information Program ) ( NASA 'SP-46 + i • GPO PRICE $ OTS PRICE(S) $ Hard copy (HC) EDITED BY Microfiche (MF) Stephen P. Maran AND A. G. W. Cameron GODDARD INSTITUTE FOR SPACE STUDIES NATIONAL AERONAUTICS AND SPACE ADMINISTRATION L 4. PHYSICSOF •NONTHERMAL RADIOSOURCES PHYSICSOF NONTHERMAL RADIOSOURCES NASA SP-46 EDITED BY Stephen P. Maran GODDARD INSTITUTE FOR SPACE STUDIES and DEPARTMENT OF ASTRONOMY UNIVERSITY OF MICHIGAN AND A. G. W. Cameron GODDARD INSTITUTE FOR SPACE STUDIES GODDARD INSTITUTE FOR SPACE STUDIES NATIONAL AERONAUTICS AND SPACE ADMINISTRATION JUNE 1964 COVER ILLUSTRATIONS Front cover-- Artist R. Catinella's impression of the central region of Messier 87, giant elliptical galaxy in the Virgo Cluster (distance approximately 36 million light years), which has been identified as a strong source of radio emission. -

Probing the Nuclear Obscuration in Radio-Galaxies with Near Infrared
Astronomy & Astrophysics manuscript no. marchesini June 15, 2018 (DOI: will be inserted by hand later) Probing the nuclear obscuration in radio-galaxies with near infrared imaging⋆,⋆⋆ D. Marchesini1,⋆⋆⋆, A. Capetti2, and A. Celotti1 1 SISSA/ISAS, Via Beirut 2-4, I-34014 Trieste, Italy 2 INAF - Osservatorio Astronomico di Torino, Strada Osservatorio 20, I-10025 Pino Torinese, Italy Received ...; accepted 08 December 2004 Abstract. We present the first near-infrared (K′-band) homogeneous observations of a complete sub-sample of the 3CR radio catalogue comprising all High Excitation Galaxies (HEGs) at z <0.3. After showing that the surface brightness decomposition technique to measure central point-like sources is affected by significant uncertainties for the objects in the studied sample, we present a new, more accurate method based on the R − K′ color profile. Via ′ this method we find a substantial nuclear K -band excess in all but two HEGs – most likely directly associated to their nuclear emission – and we measure the corresponding 2.12 µm nuclear luminosities. Within the frame of the unification scheme for radio-loud active galactic nuclei, it appears that obscuration alone is not able to account for the different nuclear properties of the majority of the HEGs and Broad Line Radio Galaxies (BLRGs), and also scattering of the (optically) hidden nuclear light from a compact region must be invoked. More precisely, for ∼70% of the HEGs the observed point-like optical emission is dominated by the scattered component, while in the ′ K -band both scattered and direct light passing through the torus contribute to the observed nuclear luminosity. -

Trans-Pacific Radio Interferometer Observations of Quasi-Stellar Objects
'ITRANS-PAC]FIC RADIO TN'IERFEROMETER OBSERVÂTTONS OF QUASI-STELLAR OBJECTSII by Jacob Samuel Gubbayt E,so., (w.1. ) Department of Physic s A thesis presented. fo r th e d.egree of Doctor of Philosophy in the Universl-ty of Ad.el-aid.e Fêbruary 197O TABLE OF CONTENTS Þo oo SUMMÂRY (r) PREFACE (') AC KIÏO'Í¡TL E DG E TI ENT S ("i ) CI{¡,PTER 1 REVT]ìü 1 CHAPTER 2 .l|l,IMS OF THE EXPERTMENIAI TNVESTICATION 9 cHAPTER 3 DISCRTPTION OF TIJ E T]XPERIMENTS 15 1.1 Bxperiments Using the Post-Detectlon Technique 15 3.2 Calcul-ation of the Dif ferential Doppler Fr e que ncy 17 3.2.1 Sources Outsid"e the Solar System 1B 1.2.2 Sources within the Solar System 20 3.2. t Assessment of th e llf f ect of the lracking lVfotion of the Antenna 22b 1 .2 .l+ Ref rac ti on 1.2.5 Scatteri-n6 and Scintillation 25 1.2.6 Rotation of the Earth About the Sun Moon and. Pl-anets 27 1.2.7 Apparent Angutar l\lotion of the Source Dtte to Prccession of 1,Ìre llarbhrs Axis 27 t.2.8 Relati.vistic T'lffects 28 3.2.9 Calculatl-on of Perameters f'or the Geometrical Configuration of the 0bservations 32 t.1 The Intermediate fnterferorneter 3h. J.h Desígn of the Bxperiments 36 3.1.+.1 Selcction of Sources lB J.11..? Cs.libration of ths Strength of the Unresolved Conponent 39 J.Ir.1 Determina.tion of Viewing Parameters )+2 paBg t. -

Planetary System Disruption by Galactic Perturbations to Wide Binary Stars
Planetary System Disruption by Galactic Perturbations to Wide Binary Stars Nathan A. Kaib1,2,3, Sean N. Raymond4,5, and Martin Duncan1 1Department of Physics, Queen’s University, Kingston, ON K7L 3N6, Canada 2Canadian Institute for Theoretical Astrophysics, University of Toronto, Toronto, ON M5S 3H8, Canada 3Dept of Physics and Astronomy & Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Northwestern University, Evanston, IL 60208, USA 4Univ. Bordeaux, LAB, UMR 5804, F-33270, Foirac, France 5CNRS, LAB, UMR 5804, F-33270, Floirac, France Nearly half of the exoplanets found within binary star systems reside in very wide binaries with average stellar separations beyond 1,000 AU1 (1 AU being the Earth-Sun distance), yet the influence of such distant binary companions on planetary evolution remains largely unstudied. Unlike their tighter counterparts, the stellar orbits of wide binaries continually change under the influence of the Galactic tide and impulses from other passing stars. Here we report numerical simulations demonstrating that the variable nature of wide binary star orbits dramatically reshapes the planetary systems they host, typically Gyrs after for- arXiv:1301.3145v1 [astro-ph.EP] 14 Jan 2013 mation. Contrary to previous understanding, wide binary companions may often strongly perturb planetary systems, triggering planetary ejections and exciting orbital eccentricities of surviving planets. Indeed, observed exoplanet eccen- tricities offer evidence of this; giant exoplanet orbits within wide binaries are statistically more eccentric than those around isolated stars. Both eccentricity 1 distributions are well-reproduced when we assume isolated stars and wide bina- ries host similar planetary systems whose outermost giant planets are scattered beyond 10 AU from their parent stars via early internal instabilities. -
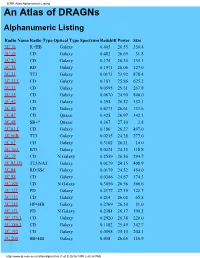
3CRR Atlas:Alphanumeric Listing an Atlas of Dragns Alphanumeric Listing
3CRR Atlas:Alphanumeric Listing An Atlas of DRAGNs Alphanumeric Listing Radio Name Radio Type Optical Type Spectrum Redshift Power Size 3C 16 R+HB Galaxy 0.405 26.55 336.4 3C 19 CD Galaxy 0.482 26.69 31.8 3C 20 CD Galaxy 0.174 26.34 135.1 3C 28 RD Galaxy 0.1971 26.06 127.0 3C 31 TTJ Galaxy 0.0173 23.92 878.4 3C 33.1 CD Galaxy 0.181 25.86 625.2 3C 33 CD Galaxy 0.0595 25.51 267.8 3C 35 CD Galaxy 0.0670 24.90 846.0 3C 42 CD Galaxy 0.395 26.52 132.1 3C 46 CD Galaxy 0.4373 26.61 733.6 3C 47 CD Quasar 0.425 26.97 342.1 3C 48 SB+? Quasar 0.367 27.10 3.8 3C 61.1 CD Galaxy 0.186 26.27 497.0 3C 66B TTJ Galaxy 0.0215 24.28 277.0 3C 67 CD Galaxy 0.3102 26.21 10.0 3C 76.1 BTJ Galaxy 0.0324 24.33 118.8 3C 79 CD N Galaxy 0.2559 26.56 294.7 3C 83.1B TTJ/NAT Galaxy 0.0179 24.15 408.9 3C 84 RD/SSC Galaxy 0.0179 24.52 454.0 3C 98 CD Galaxy 0.0306 24.87 174.3 3C 109 CD N Galaxy 0.3056 26.56 360.6 3C 123 PD Galaxy 0.2177 27.19 122.7 3C 132 CD Galaxy 0.214 26.03 65.8 3C 153 HP+HB Galaxy 0.2769 26.30 31.0 3C 171 PD N Galaxy 0.2384 26.17 109.2 3C 173.1 CD Galaxy 0.2920 26.38 220.0 3C 184.1 CD Galaxy 0.1182 25.49 342.7 3C 192 CD Galaxy 0.0598 25.10 204.1 3C 200 SB+HB Galaxy 0.458 26.65 116.9 http://www.jb.man.ac.uk/atlas/alpha.html (1 of 3) [5/26/1999 2:43:24 PM] 3CRR Atlas:Alphanumeric Listing 3C 215 R+SB Quasar 0.411 26.58 256.7 3C 219 CD Galaxy 0.1744 26.34 481.7 3C 223 CD Galaxy 0.1368 25.67 647.8 3C 234 CD N Galaxy 0.1848 26.28 300.5 3C 236 SB+HB Galaxy 0.0989 25.37 4025.6 3C 244.1 CD Galaxy 0.428 26.84 234.7 3C 249.1 HP+HB Quasar 0.311 26.27 165.1 3C 264 -

The Host Galaxy and the Extended Emission-Line Region of the Radio
ACCEPTED BY THE ASTROPHYS. J. Preprint typeset using LATEX style emulateapj v. 08/22/09 THE HOST GALAXY AND THE EXTENDED EMISSION-LINE REGION OF THE RADIO GALAXY 3C791 HAI FU AND ALAN STOCKTON Institute for Astronomy, University of Hawaii, Honolulu, HI 96822; [email protected], [email protected] Received 2007 October 10; accepted 2007 December 26 ABSTRACT We present extensive ground-based spectroscopy and HST imaging of 3C79, an FRII radio galaxy associated with a luminous extended emission-line region (EELR). Surface brightness modeling of an emission-line- free HST R-band image reveals that the host galaxy is a massive elliptical with a compact companion 0.′′8 away and 4 magnitudes fainter. The host galaxy spectrum is best described by an intermediate-age (1.3 Gyr) stellar population (4% by mass), superimposed on a 10 Gyr old population and a power law (αλ = −1.8); the stellar populations are consistent with super-solar metallicities, with the best fit given by the 2.5 Z⊙ models. 11 We derive a dynamical mass of 4 × 10 M⊙ within the effective radius from the velocity dispersion. The EELR spectra clearly indicate that the EELR is photoionized by the hidden central engine. Photoionization modeling shows evidence that the gas metallicity in both the EELR and the nuclear narrow-line region is mildly sub-solar (0.3 − 0.7 Z⊙) — significantly lower than the super-solar metallicities deduced from typical active galactic nuclei in the Sloan Digital Sky Survey. The more luminous filaments in the EELR exhibit a velocity field consistent with a common disk rotation.