DOCSLIB.ORG

Dynamics of Saturn's Small Moons in Coupled First Order Planar Resonances

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Dynamics of Saturn's Small Moons in Coupled First Order Planar Resonances Dynamics of Saturn's small moons in coupled first order planar resonances Maryame El Moutamid Bruno Sicardy and St´efanRenner LESIA/IMCCE | Paris Observatory 26 juin 2012 Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Saturn system Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Very small moons Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk New satellites : Anthe, Methone and Aegaeon (Cooper et al., 2008 ; Hedman et al., 2009, 2010 ; Porco et al., 2005) Very small (0.5 km to 2 km) Vicinity of the Mimas orbit (outside and inside) The aims of the work A better understanding : - of the dynamics of this population of news satellites - of the scenario of capture into mean motion resonances Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Dynamical structure of the system µ µ´ Mp We consider only : - The resonant terms - The secular terms causing the precessions of the orbit When µ ! 0 ) The symmetry is broken ) different kinds of resonances : - Lindblad Resonance - Corotation Resonance D'Alembert rules : 0 0 c = (m + 1)λ − mλ − $ 0 L = (m + 1)λ − mλ − $ Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Corotation Resonance - Aegaeon (7/6) : c = 7λMimas − 6λAegaeon − $Mimas - Methone (14/15) : c = 15λMethone − 14λMimas − $Mimas - Anthe (10/11) : c = 11λAnthe − 10λMimas − $Mimas Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Corotation resonances Mean motion resonance : n1 = m+q n2 m Particular case : Lagrangian Equilibrium Points Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Adam's ring and Galatea Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Corotation resonances : Pendular motion 8 χ_ = − sin( ) 8 χ = 3 m a−ac < c c c < c 2 a where : : _ : = 3m2 Ms a Ee c = χc c Mp ac s 3 2 1 c J 0 -1 -2 -3 -200 -150 -100 -50 0 50 100 150 200 sc (deg) Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Lindblad Resonance 8 h_ = + @H = −(J − J + D)k < @k C L (1) : _ @H k = − @h = +(JC − JL + D)h + "L 8 < h / e cos( L) e=(h,k) : the vector eccentricity : k / e sin( L) e2 JL / 2 2 HAnd = JL − (Jc + D)JL − "Lh Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Dynamical study Equations of motions ) The Coralin (CORotation And LINdblad) Model 0 0 c = (m + 1)λ − mλ − $ near _c = 0 0 L = (m + 1)λ − mλ − $ near _L = 0 The coupling leads to a chaotic motion Asymptotic cases General solutions based on adiabatic invariance arguments Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Hamiltonian formalism : The Coralin Model 8 @H J_c = − = − sin( c ) > @ c > > > @H > _c = + = JC − [JL] <> @Jc (2) > h_ = + @H = −([J ] − J + D)k > @k C L > > :> _ @H k = − @h = +([JC ] − JL + D)h + "L where the Hamiltonian H is given by : p 1 2 H(Jc ; C ; JL; L) = 2 (Jc − JL) − DJL − cos( C ) − "L 3jmje cos( L) where : 8 < h / e cos( L) e=(h,k) : the vector eccentricity : k / e sin( L) e2 JL / 2 Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk To simplify 3 Jc-JL 2 1 2 -D 0 sc -1 -2 -3 -4 -3 -2 -1 0 1 2 3 4 This study depends essentially of D which gives the distance between the two resonances, and the forcing value "L for a given value of the width of CER. D "L Anthe 0.256 -0.133 Aegaeon -1.34 0.132 Methone 0.122 -0.115 Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Case Anthe Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Probability of capturing into the Corotation Eccentric Resonance (CER) - add migration in the CoraLin model to estimate the capture probabilities into CER perturbed by LER Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Hamiltonian formalism with migration 8 J_ = − sin( ) +_a=2a > c c > > > _ <> c = JC − JL = χ (3) > _ > h = −(JC − JL + D)k > > > : k_ = +(JC − JL + D)h + "L Tav =a _=2a = α + βχ Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk constant torque : No capture Tav = α 80 60 40 20 c J 0 -20 -40 -60 -80 -200 -150 -100 -50 0 50 100 150 200 sc (deg) Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk torque with gradient : possible capture Tav = α + βχ 80 60 40 20 c J 0 -20 -40 -60 -200 -150 -100 -50 0 50 100 150 200 sc (deg) Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Torque with gradient Tav = α + βχ 50 0.005 40 0.0045 30 0.004 20 0.0035 10 0.003 0 0.0025 -10 Eccentricity 0.002 Semi-major axis -20 0.0015 -30 -40 0.001 -50 0.0005 -60 0 0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1e+06 0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1e+06 Time (days) Time (days) a = 197655.4 km e = 0.003 Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Case Anthe Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Case Anthe Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk Conclusions and prospects - CoraLin : simple model to investigate the dynamics of a satellite on CER/LER - Capture probabilities into CER + applications to our satellites - Anthe crosses a chaotic region favors the capture - The capture is sure in the second scenario - For Aegaeon : need a migration in the other direction. Maryame El Moutamid ESLAB-2012 | ESA/ESTEC Noordwijk.
Load more

Recommended publications
  • Arxiv:1912.09192V2 [Astro-Ph.EP] 24 Feb 2020
    Draft version February 25, 2020 Typeset using LATEX preprint style in AASTeX62 Photometric analyses of Saturn's small moons: Aegaeon, Methone and Pallene are dark; Helene and Calypso are bright. M. M. Hedman,1 P. Helfenstein,2 R. O. Chancia,1, 3 P. Thomas,2 E. Roussos,4 C. Paranicas,5 and A. J. Verbiscer6 1Department of Physics, University of Idaho, Moscow, ID 83844 2Cornell Center for Astrophysics and Planetary Science, Cornell University, Ithaca NY 14853 3Center for Imaging Science, Rochester Institute of Technology, Rochester NY 14623 4Max Planck Institute for Solar System Research, G¨ottingen,Germany 37077 5APL, John Hopkins University, Laurel MD 20723 6Department of Astronomy, University of Virginia, Charlottesville, VA 22904 ABSTRACT We examine the surface brightnesses of Saturn's smaller satellites using a photometric model that explicitly accounts for their elongated shapes and thus facilitates compar- isons among different moons. Analyses of Cassini imaging data with this model reveals that the moons Aegaeon, Methone and Pallene are darker than one would expect given trends previously observed among the nearby mid-sized satellites. On the other hand, the trojan moons Calypso and Helene have substantially brighter surfaces than their co-orbital companions Tethys and Dione. These observations are inconsistent with the moons' surface brightnesses being entirely controlled by the local flux of E-ring par- ticles, and therefore strongly imply that other phenomena are affecting their surface properties. The darkness of Aegaeon, Methone and Pallene is correlated with the fluxes of high-energy protons, implying that high-energy radiation is responsible for darkening these small moons. Meanwhile, Prometheus and Pandora appear to be brightened by their interactions with nearby dusty F ring, implying that enhanced dust fluxes are most likely responsible for Calypso's and Helene's excess brightness.
    [Show full text]
  • Cassini Update
    Cassini Update Dr. Linda Spilker Cassini Project Scientist Outer Planets Assessment Group 22 February 2017 Sols%ce Mission Inclina%on Profile equator Saturn wrt Inclination 22 February 2017 LJS-3 Year 3 Key Flybys Since Aug. 2016 OPAG T124 – Titan flyby (1584 km) • November 13, 2016 • LAST Radio Science flyby • One of only two (cf. T106) ideal bistatic observations capturing Titan’s Northern Seas • First and only bistatic observation of Punga Mare • Western Kraken Mare not explored by RSS before T125 – Titan flyby (3158 km) • November 29, 2016 • LAST Optical Remote Sensing targeted flyby • VIMS high-resolution map of the North Pole looking for variations at and around the seas and lakes. • CIRS last opportunity for vertical profile determination of gases (e.g. water, aerosols) • UVIS limb viewing opportunity at the highest spatial resolution available outside of occultations 22 February 2017 4 Interior of Hexagon Turning “Less Blue” • Bluish to golden haze results from increased production of photochemical hazes as north pole approaches summer solstice. • Hexagon acts as a barrier that prevents haze particles outside hexagon from migrating inward. • 5 Refracting Atmosphere Saturn's• 22unlit February rings appear 2017 to bend as they pass behind the planet’s darkened limb due• 6 to refraction by Saturn's upper atmosphere. (Resolution 5 km/pixel) Dione Harbors A Subsurface Ocean Researchers at the Royal Observatory of Belgium reanalyzed Cassini RSS gravity data• 7 of Dione and predict a crust 100 km thick with a global ocean 10’s of km deep. Titan’s Summer Clouds Pose a Mystery Why would clouds on Titan be visible in VIMS images, but not in ISS images? ISS ISS VIMS High, thin cirrus clouds that are optically thicker than Titan’s atmospheric haze at longer VIMS wavelengths,• 22 February but optically 2017 thinner than the haze at shorter ISS wavelengths, could be• 8 detected by VIMS while simultaneously lost in the haze to ISS.
    [Show full text]
  • 7 Planetary Rings Matthew S
    7 Planetary Rings Matthew S. Tiscareno Center for Radiophysics and Space Research, Cornell University, Ithaca, NY, USA 1Introduction..................................................... 311 1.1 Orbital Elements ..................................................... 312 1.2 Roche Limits, Roche Lobes, and Roche Critical Densities .................... 313 1.3 Optical Depth ....................................................... 316 2 Rings by Planetary System .......................................... 317 2.1 The Rings of Jupiter ................................................... 317 2.2 The Rings of Saturn ................................................... 319 2.3 The Rings of Uranus .................................................. 320 2.4 The Rings of Neptune ................................................. 323 2.5 Unconfirmed Ring Systems ............................................. 324 2.5.1 Mars ............................................................... 324 2.5.2 Pluto ............................................................... 325 2.5.3 Rhea and Other Moons ................................................ 325 2.5.4 Exoplanets ........................................................... 327 3RingsbyType.................................................... 328 3.1 Dense Broad Disks ................................................... 328 3.1.1 Spiral Waves ......................................................... 329 3.1.2 Gap Edges and Moonlet Wakes .......................................... 333 3.1.3 Radial Structure .....................................................
    [Show full text]
  • The Orbits of Saturn's Small Satellites Derived From
    The Astronomical Journal, 132:692–710, 2006 August A # 2006. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE ORBITS OF SATURN’S SMALL SATELLITES DERIVED FROM COMBINED HISTORIC AND CASSINI IMAGING OBSERVATIONS J. N. Spitale CICLOPS, Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO 80301; [email protected] R. A. Jacobson Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109-8099 C. C. Porco CICLOPS, Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO 80301 and W. M. Owen, Jr. Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109-8099 Received 2006 February 28; accepted 2006 April 12 ABSTRACT We report on the orbits of the small, inner Saturnian satellites, either recovered or newly discovered in recent Cassini imaging observations. The orbits presented here reflect improvements over our previously published values in that the time base of Cassini observations has been extended, and numerical orbital integrations have been performed in those cases in which simple precessing elliptical, inclined orbit solutions were found to be inadequate. Using combined Cassini and Voyager observations, we obtain an eccentricity for Pan 7 times smaller than previously reported because of the predominance of higher quality Cassini data in the fit. The orbit of the small satellite (S/2005 S1 [Daphnis]) discovered by Cassini in the Keeler gap in the outer A ring appears to be circular and coplanar; no external perturbations are appar- ent. Refined orbits of Atlas, Prometheus, Pandora, Janus, and Epimetheus are based on Cassini , Voyager, Hubble Space Telescope, and Earth-based data and a numerical integration perturbed by all the massive satellites and each other.
    [Show full text]
  • Planetary Rings
    CLBE001-ESS2E November 10, 2006 21:56 100-C 25-C 50-C 75-C C+M 50-C+M C+Y 50-C+Y M+Y 50-M+Y 100-M 25-M 50-M 75-M 100-Y 25-Y 50-Y 75-Y 100-K 25-K 25-19-19 50-K 50-40-40 75-K 75-64-64 Planetary Rings Carolyn C. Porco Space Science Institute Boulder, Colorado Douglas P. Hamilton University of Maryland College Park, Maryland CHAPTER 27 1. Introduction 5. Ring Origins 2. Sources of Information 6. Prospects for the Future 3. Overview of Ring Structure Bibliography 4. Ring Processes 1. Introduction houses, from coalescing under their own gravity into larger bodies. Rings are arranged around planets in strikingly dif- Planetary rings are those strikingly flat and circular ap- ferent ways despite the similar underlying physical pro- pendages embracing all the giant planets in the outer Solar cesses that govern them. Gravitational tugs from satellites System: Jupiter, Saturn, Uranus, and Neptune. Like their account for some of the structure of densely-packed mas- cousins, the spiral galaxies, they are formed of many bod- sive rings [see Solar System Dynamics: Regular and ies, independently orbiting in a central gravitational field. Chaotic Motion], while nongravitational effects, includ- Rings also share many characteristics with, and offer in- ing solar radiation pressure and electromagnetic forces, valuable insights into, flattened systems of gas and collid- dominate the dynamics of the fainter and more diffuse dusty ing debris that ultimately form solar systems. Ring systems rings. Spacecraft flybys of all of the giant planets and, more are accessible laboratories capable of providing clues about recently, orbiters at Jupiter and Saturn, have revolutionized processes important in these circumstellar disks, structures our understanding of planetary rings.
    [Show full text]
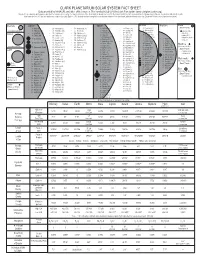
  • CLARK PLANETARIUM SOLAR SYSTEM FACT SHEET Data Provided by NASA/JPL and Other Official Sources
    CLARK PLANETARIUM SOLAR SYSTEM FACT SHEET Data provided by NASA/JPL and other official sources. This handout ©July 2013 by Clark Planetarium (www.clarkplanetarium.org). May be freely copied by professional educators for classroom use only. The known satellites of the Solar System shown here next to their planets with their sizes (mean diameter in km) in parenthesis. The planets and satellites (with diameters above 1,000 km) are depicted in relative size (with Earth = 0.500 inches) and are arranged in order by their distance from the planet, with the closest at the top. Distances from moon to planet are not listed. Mercury Jupiter Saturn Uranus Neptune Pluto • 1- Metis (44) • 26- Hermippe (4) • 54- Hegemone (3) • 1- S/2009 S1 (1) • 33- Erriapo (10) • 1- Cordelia (40.2) (Dwarf Planet) (no natural satellites) • 2- Adrastea (16) • 27- Praxidike (6.8) • 55- Aoede (4) • 2- Pan (26) • 34- Siarnaq (40) • 2- Ophelia (42.8) • Charon (1186) • 3- Bianca (51.4) Venus • 3- Amalthea (168) • 28- Thelxinoe (2) • 56- Kallichore (2) • 3- Daphnis (7) • 35- Skoll (6) • Nix (60?) • 4- Thebe (98) • 29- Helike (4) • 57- S/2003 J 23 (2) • 4- Atlas (32) • 36- Tarvos (15) • 4- Cressida (79.6) • Hydra (50?) • 5- Desdemona (64) • 30- Iocaste (5.2) • 58- S/2003 J 5 (4) • 5- Prometheus (100.2) • 37- Tarqeq (7) • Kerberos (13-34?) • 5- Io (3,643.2) • 6- Pandora (83.8) • 38- Greip (6) • 6- Juliet (93.6) • 1- Naiad (58) • 31- Ananke (28) • 59- Callirrhoe (7) • Styx (??) • 7- Epimetheus (119) • 39- Hyrrokkin (8) • 7- Portia (135.2) • 2- Thalassa (80) • 6- Europa (3,121.6)
    [Show full text]
  • Observing the Universe
    ObservingObserving thethe UniverseUniverse :: aa TravelTravel ThroughThrough SpaceSpace andand TimeTime Enrico Flamini Agenzia Spaziale Italiana Tokyo 2009 When you rise your head to the night sky, what your eyes are observing may be astonishing. However it is only a small portion of the electromagnetic spectrum of the Universe: the visible . But any electromagnetic signal, indipendently from its frequency, travels at the speed of light. When we observe a star or a galaxy we see the photons produced at the moment of their production, their travel could have been incredibly long: it may be lasted millions or billions of years. Looking at the sky at frequencies much higher then visible, like in the X-ray or gamma-ray energy range, we can observe the so called “violent sky” where extremely energetic fenoena occurs.like Pulsar, quasars, AGN, Supernova CosmicCosmic RaysRays:: messengersmessengers fromfrom thethe extremeextreme universeuniverse We cannot see the deep universe at E > few TeV, since photons are attenuated through →e± on the CMB + IR backgrounds. But using cosmic rays we should be able to ‘see’ up to ~ 6 x 1010 GeV before they get attenuated by other interaction. Sources Sources → Primordial origin Primordial 7 Redshift z = 0 (t = 13.7 Gyr = now ! ) Going to a frequency lower then the visible light, and cooling down the instrument nearby absolute zero, it’s possible to observe signals produced millions or billions of years ago: we may travel near the instant of the formation of our universe: 13.7 By. Redshift z = 1.4 (t = 4.7 Gyr) Credits A. Cimatti Univ. Bologna Redshift z = 5.7 (t = 1 Gyr) Credits A.
    [Show full text]
  • Long-Term Evolution and Stability of Saturnian Small Satellites
    MNRAS 000, 1–17 (2016) Preprint 30 August 2021 Compiled using MNRAS LATEX style file v3.0 Long-term Evolution and Stability of Saturnian Small Satellites: Aegaeon, Methone, Anthe, and Pallene. M. A. Mun˜oz-Guti´errez,1⋆ and S. Giuliatti Winter1 1Universidade Estadual Paulista - UNESP, Grupo de Dinˆamica Orbital e Planetologia, Av. Ariberto Pereira da Cunha, 333, Guaratinguet´a-SP, 12516-410, Brazil Accepted XXX. Received YYY; in original form ZZZ ABSTRACT Aegaeon, Methone, Anthe, and Pallene are four Saturnian small moons, discovered by the Cassini spacecraft. Although their orbital characterization has been carried on by a number of authors, their long-term evolution has not been studied in detail so far. In this work, we numerically explore the long-term evolution, up to 105 yr, of the small moons in a system formed by an oblate Saturn and the five largest moons close to the region: Janus, Epimetheus, Mimas, Enceladus, and Tethys. By using frequency analysis we determined the stability of the small moons and characterize, through diffusion maps, the dynamical behavior of a wide region of geometric phase space, a vs e, surrounding them. Those maps could shed light on the possible initial number of small bodies close to Mimas, and help to better understand the dynamical origin of the small satellites. We found that the four small moons are long-term stable and no mark of chaos is found for them. Aegaeon, Methone, and Anthe could remain unaltered for at least ∼ 0.5Myr, given the current configuration of the system. They remain well- trapped in the corotation eccentricity resonances with Mimas in which they currently librate.
    [Show full text]
  • An Analytical Model for the Dust Environment Around Saturn's
    EPSC Abstracts Vol. 9, EPSC2014-310, 2014 European Planetary Science Congress 2014 EEuropeaPn PlanetarSy Science CCongress c Author(s) 2014 An Analytical Model for the Dust Environment around Saturn’s Moons Pallene, Methone and Anthe Michael Seiler, Martin Seiß, Kai-Lung Sun and Frank Spahn Institute of Physics and Astronomy, University of Potsdam, Germany ([email protected]) Abstract Acknowledgements Since its arrival at Saturn in 2004 the observations This work was supported by the Deutsche Forschungs- by the spacecraft Cassini have revolutionised the gemeinschaft (Sp 384/28-1, Sp 384/21-2) and the understanding of the dynamics in planetary rings. Deutsches Zentrum für Luft- und Raumfahrt (OH By analysing Cassini images, Hedman et al. [1] 0003). detected faint dust along the orbits of Saturn’s tiny moons Methone, Anthe and Pallene. While the ring material around Methone and Anthe appears to be References longitudinally confined to arcs, a continuous ring of material has been observed around the orbit of Pallene [1] Hedman, M. M. et al., "Three tenuous rings/arcs for three tiny moons", Icarus, 199, pp. 378-386, 2009 by the Cassini dust analyzer. The data show, that at least part of the torus lies exterior Pallene’s orbit. [2] Cooper, N. J. et al. "Astrometry and dynamics of Anthe (S/2007 S 4), a new satellite of Saturn", Icarus, 195, pp. Many tiny moons are located between Mimas and 765-777, 2008 Enceladus and are known to be resonantly perturbed [3] Spitale, J. N. et al. "The Orbits of Saturn’s Small Satel- by these [2, 3].
    [Show full text]
  • THE SATURNIAN G RING: a SHORT NOTE ABOUT ITS FORMATION Revista Mexicana De Astronomía Y Astrofísica, Vol
    Revista Mexicana de Astronomía y Astrofísica ISSN: 0185-1101 [email protected] Instituto de Astronomía México Maravilla, D.; Leal-Herrera, J. L. THE SATURNIAN G RING: A SHORT NOTE ABOUT ITS FORMATION Revista Mexicana de Astronomía y Astrofísica, vol. 50, núm. 2, octubre, 2014, pp. 341- 347 Instituto de Astronomía Distrito Federal, México Available in: http://www.redalyc.org/articulo.oa?id=57148278016 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative Revista Mexicana de Astronom´ıa y Astrof´ısica, 50, 341–347 (2014) THE SATURNIAN G RING: A SHORT NOTE ABOUT ITS FORMATION D. Maravilla and J. L. Leal-Herrera Departamento de Ciencias Espaciales, Instituto de Geof´ısica, UNAM, Mexico Received March 21 2014; accepted August 18 2014 RESUMEN En este trabajo se estudia la formaci´on del anillo G de Saturno considerando que el sat´elite Ege´on es la fuente de part´ıculas de polvo. El polvo que forma el anillo se produce por impactos entre los micrometeoroides interplanetarios que ingresan en la magnet´osfera Saturniana y la superficie de Ege´on. Para explicar c´omo se forma el anillo se usa un modelo gravito-electrodin´amico suponiendo que las fuerzas gravitacional y electromagn´etica son las ´unicas fuerzas que modulan el comportamiento din´amico de las part´ıculas de polvo. Las soluciones del modelo muestran que existen reg´ımenes de confinamiento (captura) as´ıcomo reg´ımenes de escape de polvo en la vecindad de Ege´on.
    [Show full text]
  • Resonant Moons of Neptune
    EPSC Abstracts Vol. 13, EPSC-DPS2019-901-1, 2019 EPSC-DPS Joint Meeting 2019 c Author(s) 2019. CC Attribution 4.0 license. Resonant moons of Neptune Marina Brozović (1), Mark R. Showalter (2), Robert A. Jacobson (1), Robert S. French (2), Jack L. Lissauer (3), Imke de Pater (4) (1) Jet Propulsion Laboratory, California Institute of Technology, California, USA, (2) SETI Institute, California, USA, (3) NASA Ames Research Center, California, USA, (4) University of California Berkeley, California, USA Abstract We used integrated orbits to fit astrometric data of the 2. Methods regular moons of Neptune. We found a 73:69 inclination resonance between Naiad and Thalassa, the 2.1 Observations two innermost moons. Their resonant argument librates around 180° with an average amplitude of The astrometric data cover the period from 1981-2016, ~66° and a period of ~1.9 years. This is the first fourth- with the most significant amount of data originating order resonance discovered between the moons of the from the Voyager 2 spacecraft and HST. Voyager 2 outer planets. The resonance enabled an estimate of imaged all regular satellites except Hippocamp the GMs for Naiad and Thalassa, GMN= between 1989 June 7 and 1989 August 24. The follow- 3 -2 3 0.0080±0.0043 km s and GMT=0.0236±0.0064 km up observations originated from several Earth-based s-2. More high-precision astrometry of Naiad and telescopes, but the majority were still obtained by HST. Thalassa will help better constrain their masses. The [4] published the latest set of the HST astrometry GMs of Despina, Galatea, and Larissa are more including the discovery and follow up observations of difficult to measure because they are not in any direct Hippocamp.
    [Show full text]
  • Moons of Saturn
    National Aeronautics and Space Administration 0 300,000,000 900,000,000 1,500,000,000 2,100,000,000 2,700,000,000 3,300,000,000 3,900,000,000 4,500,000,000 5,100,000,000 5,700,000,000 kilometers Moons of Saturn www.nasa.gov Saturn, the sixth planet from the Sun, is home to a vast array • Phoebe orbits the planet in a direction opposite that of Saturn’s • Fastest Orbit Pan of intriguing and unique satellites — 53 plus 9 awaiting official larger moons, as do several of the recently discovered moons. Pan’s Orbit Around Saturn 13.8 hours confirmation. Christiaan Huygens discovered the first known • Mimas has an enormous crater on one side, the result of an • Number of Moons Discovered by Voyager 3 moon of Saturn. The year was 1655 and the moon is Titan. impact that nearly split the moon apart. (Atlas, Prometheus, and Pandora) Jean-Dominique Cassini made the next four discoveries: Iapetus (1671), Rhea (1672), Dione (1684), and Tethys (1684). Mimas and • Enceladus displays evidence of active ice volcanism: Cassini • Number of Moons Discovered by Cassini 6 Enceladus were both discovered by William Herschel in 1789. observed warm fractures where evaporating ice evidently es- (Methone, Pallene, Polydeuces, Daphnis, Anthe, and Aegaeon) The next two discoveries came at intervals of 50 or more years capes and forms a huge cloud of water vapor over the south — Hyperion (1848) and Phoebe (1898). pole. ABOUT THE IMAGES As telescopic resolving power improved, Saturn’s family of • Hyperion has an odd flattened shape and rotates chaotically, 1 2 3 1 Cassini’s visual known moons grew.
    [Show full text]