14.0 Dimensioning 14.1 Dimension Setup and Preparation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Descriptive Geometry Section 10.1 Basic Descriptive Geometry and Board Drafting Section 10.2 Solving Descriptive Geometry Problems with CAD
10 Descriptive Geometry Section 10.1 Basic Descriptive Geometry and Board Drafting Section 10.2 Solving Descriptive Geometry Problems with CAD Chapter Objectives • Locate points in three-dimensional (3D) space. • Identify and describe the three basic types of lines. • Identify and describe the three basic types of planes. • Solve descriptive geometry problems using board-drafting techniques. • Create points, lines, planes, and solids in 3D space using CAD. • Solve descriptive geometry problems using CAD. Plane Spoken Rutan’s unconventional 202 Boomerang aircraft has an asymmetrical design, with one engine on the fuselage and another mounted on a pod. What special allowances would need to be made for such a design? 328 Drafting Career Burt Rutan, Aeronautical Engineer Effi cient travel through space has become an ambi- tion of aeronautical engineer, Burt Rutan. “I want to go high,” he says, “because that’s where the view is.” His unconventional designs have included every- thing from crafts that can enter space twice within a two week period, to planes than can circle the Earth without stopping to refuel. Designed by Rutan and built at his company, Scaled Composites LLC, the 202 Boomerang aircraft is named for its forward-swept asymmetrical wing. The design allows the Boomerang to fl y faster and farther than conventional twin-engine aircraft, hav- ing corrected aerodynamic mistakes made previously in twin-engine design. It is hailed as one of the most beautiful aircraft ever built. Academic Skills and Abilities • Algebra, geometry, calculus • Biology, chemistry, physics • English • Social studies • Humanities • Computer use Career Pathways Engineers should be creative, inquisitive, ana- lytical, detail oriented, and able to work as part of a team and to communicate well. -
1-1 Understanding Points, Lines, and Planes Lines, and Planes
Understanding Points, 1-11-1 Understanding Points, Lines, and Planes Lines, and Planes Holt Geometry 1-1 Understanding Points, Lines, and Planes Objectives Identify, name, and draw points, lines, segments, rays, and planes. Apply basic facts about points, lines, and planes. Holt Geometry 1-1 Understanding Points, Lines, and Planes Vocabulary undefined term point line plane collinear coplanar segment endpoint ray opposite rays postulate Holt Geometry 1-1 Understanding Points, Lines, and Planes The most basic figures in geometry are undefined terms, which cannot be defined by using other figures. The undefined terms point, line, and plane are the building blocks of geometry. Holt Geometry 1-1 Understanding Points, Lines, and Planes Holt Geometry 1-1 Understanding Points, Lines, and Planes Points that lie on the same line are collinear. K, L, and M are collinear. K, L, and N are noncollinear. Points that lie on the same plane are coplanar. Otherwise they are noncoplanar. K L M N Holt Geometry 1-1 Understanding Points, Lines, and Planes Example 1: Naming Points, Lines, and Planes A. Name four coplanar points. A, B, C, D B. Name three lines. Possible answer: AE, BE, CE Holt Geometry 1-1 Understanding Points, Lines, and Planes Holt Geometry 1-1 Understanding Points, Lines, and Planes Example 2: Drawing Segments and Rays Draw and label each of the following. A. a segment with endpoints M and N. N M B. opposite rays with a common endpoint T. T Holt Geometry 1-1 Understanding Points, Lines, and Planes Check It Out! Example 2 Draw and label a ray with endpoint M that contains N. -

Machine Drawing
2.4 LINES Lines of different types and thicknesses are used for graphical representation of objects. The types of lines and their applications are shown in Table 2.4. Typical applications of different types of lines are shown in Figs. 2.5 and 2.6. Table 2.4 Types of lines and their applications Line Description General Applications A Continuous thick A1 Visible outlines B Continuous thin B1 Imaginary lines of intersection (straight or curved) B2 Dimension lines B3 Projection lines B4 Leader lines B5 Hatching lines B6 Outlines of revolved sections in place B7 Short centre lines C Continuous thin, free-hand C1 Limits of partial or interrupted views and sections, if the limit is not a chain thin D Continuous thin (straight) D1 Line (see Fig. 2.5) with zigzags E Dashed thick E1 Hidden outlines G Chain thin G1 Centre lines G2 Lines of symmetry G3 Trajectories H Chain thin, thick at ends H1 Cutting planes and changes of direction J Chain thick J1 Indication of lines or surfaces to which a special requirement applies K Chain thin, double-dashed K1 Outlines of adjacent parts K2 Alternative and extreme positions of movable parts K3 Centroidal lines 2.4.2 Order of Priority of Coinciding Lines When two or more lines of different types coincide, the following order of priority should be observed: (i) Visible outlines and edges (Continuous thick lines, type A), (ii) Hidden outlines and edges (Dashed line, type E or F), (iii) Cutting planes (Chain thin, thick at ends and changes of cutting planes, type H), (iv) Centre lines and lines of symmetry (Chain thin line, type G), (v) Centroidal lines (Chain thin double dashed line, type K), (vi) Projection lines (Continuous thin line, type B). -

A Historical Introduction to Elementary Geometry
i MATH 119 – Fall 2012: A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning “earth measure” ( ge = earth or land ) + ( metria = measure ) . Euclid wrote the Elements of geometry between 330 and 320 B.C. It was a compilation of the major theorems on plane and solid geometry presented in an axiomatic style. Near the beginning of the first of the thirteen books of the Elements, Euclid enumerated five fundamental assumptions called postulates or axioms which he used to prove many related propositions or theorems on the geometry of two and three dimensions. POSTULATE 1. Any two points can be joined by a straight line. POSTULATE 2. Any straight line segment can be extended indefinitely in a straight line. POSTULATE 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. POSTULATE 4. All right angles are congruent. POSTULATE 5. (Parallel postulate) If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. The circle described in postulate 3 is tacitly unique. Postulates 3 and 5 hold only for plane geometry; in three dimensions, postulate 3 defines a sphere. Postulate 5 leads to the same geometry as the following statement, known as Playfair's axiom, which also holds only in the plane: Through a point not on a given straight line, one and only one line can be drawn that never meets the given line. -

Geometry Course Outline
GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid -
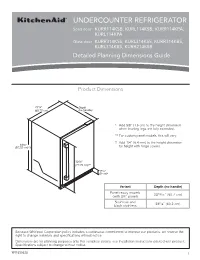
Dimension Guide
UNDERCOUNTER REFRIGERATOR Solid door KURR114KSB, KURL114KSB, KURR114KPA, KURL114KPA Glass door KURR314KSS, KURL314KSS, KURR314KBS, KURL314KBS, KURR214KSB Detailed Planning Dimensions Guide Product Dimensions 237/8” Depth (60.72 cm) (no handle) * Add 5/8” (1.6 cm) to the height dimension when leveling legs are fully extended. ** For custom panel models, this will vary. † Add 1/4” (6.4 mm) to the height dimension 343/8” (87.32 cm)*† for height with hinge covers. 305/8” (77.75 cm)** 39/16” (9 cm)* Variant Depth (no handle) Panel ready models 2313/16” (60.7 cm) (with 3/4” panel) Stainless and 235/8” (60.2 cm) black stainless Because Whirlpool Corporation policy includes a continuous commitment to improve our products, we reserve the right to change materials and specifications without notice. Dimensions are for planning purposes only. For complete details, see Installation Instructions packed with product. Specifications subject to change without notice. W11530525 1 Panel ready models Stainless and black Dimension Description (with 3/4” panel) stainless models A Width of door 233/4” (60.3 cm) 233/4” (60.3 cm) B Width of the grille 2313/16” (60.5 cm) 2313/16” (60.5 cm) C Height to top of handle ** 311/8” (78.85 cm) Width from side of refrigerator to 1 D handle – door open 90° ** 2 /3” (5.95 cm) E Depth without door 2111/16” (55.1 cm) 2111/16” (55.1 cm) F Depth with door 2313/16” (60.7 cm) 235/8” (60.2 cm) 7 G Depth with handle ** 26 /16” (67.15 cm) H Depth with door open 90° 4715/16” (121.8 cm) 4715/16” (121.8 cm) **For custom panel models, this will vary. -

13 Graphs 13.2D Lengths of Line Segments
MEP Pupil Text 13-19, Additional Material 13 Graphs 13.2D Lengths of Line Segments In a right-angled triangle the length of the hypotenuse may be calculated using Pythagoras' Theorem. c b cab222=+ a Worked Example 1 Determine the length of the line segment joining the points A (4, 1) and B (10, 9). Solution y (a) The diagram shows the two points and the line segment that joins them. 10 B A right-angled triangle has been 9 drawn under the line segment. The 8 length of the line segment AB (the 7 hypotenuse) may be found by using 6 Pythagoras' Theorem. 5 8 4 AB2 =+62 82 3 2 =+ 2 AB 36 64 A 6 1 AB2 = 100 0 12345678910 x AB = 100 AB = 10 Worked Example 2 y C Determine the length of the line 8 7 joining the points C (−48, ) 6 (−) and D 86, . 5 4 Solution 3 2 14 The diagram shows the two points 1 and a right-angled triangle that can –4 –3 –2 –1 0 12345678 x be used to determine the length of –1 the line segment CD. –2 –3 –4 –5 D –6 12 1 13.2D MEP Pupil Text 13-19, Additional Material Using Pythagoras' Theorem, CD2 =+142 122 CD2 =+196 144 CD2 = 340 CD = 340 CD = 18. 43908891 CD = 18. 4 (to 3 significant figures) Exercises 1. The diagram shows the three points y C A, B and C which are the vertices 11 of a triangle. 10 9 (a) State the length of the line 8 segment AB. -

Spectral Dimensions and Dimension Spectra of Quantum Spacetimes
PHYSICAL REVIEW D 102, 086003 (2020) Spectral dimensions and dimension spectra of quantum spacetimes † Michał Eckstein 1,2,* and Tomasz Trześniewski 3,2, 1Institute of Theoretical Physics and Astrophysics, National Quantum Information Centre, Faculty of Mathematics, Physics and Informatics, University of Gdańsk, ulica Wita Stwosza 57, 80-308 Gdańsk, Poland 2Copernicus Center for Interdisciplinary Studies, ulica Szczepańska 1/5, 31-011 Kraków, Poland 3Institute of Theoretical Physics, Jagiellonian University, ulica S. Łojasiewicza 11, 30-348 Kraków, Poland (Received 11 June 2020; accepted 3 September 2020; published 5 October 2020) Different approaches to quantum gravity generally predict that the dimension of spacetime at the fundamental level is not 4. The principal tool to measure how the dimension changes between the IR and UV scales of the theory is the spectral dimension. On the other hand, the noncommutative-geometric perspective suggests that quantum spacetimes ought to be characterized by a discrete complex set—the dimension spectrum. We show that these two notions complement each other and the dimension spectrum is very useful in unraveling the UV behavior of the spectral dimension. We perform an extended analysis highlighting the trouble spots and illustrate the general results with two concrete examples: the quantum sphere and the κ-Minkowski spacetime, for a few different Laplacians. In particular, we find that the spectral dimensions of the former exhibit log-periodic oscillations, the amplitude of which decays rapidly as the deformation parameter tends to the classical value. In contrast, no such oscillations occur for either of the three considered Laplacians on the κ-Minkowski spacetime. DOI: 10.1103/PhysRevD.102.086003 I. -

Zero-Dimensional Symmetry
Snapshots of modern mathematics № 3/2015 from Oberwolfach Zero-dimensional symmetry George Willis This snapshot is about zero-dimensional symmetry. Thanks to recent discoveries we now understand such symmetry better than previously imagined possible. While still far from complete, a picture of zero-dimen- sional symmetry is beginning to emerge. 1 An introduction to symmetry: spinning globes and infinite wallpapers Let’s begin with an example. Think of a sphere, for example a globe’s surface. Every point on it is specified by two parameters, longitude and latitude. This makes the sphere a two-dimensional surface. You can rotate the globe along an axis through the center; the object you obtain after the rotation still looks like the original globe (although now maybe New York is where the Mount Everest used to be), meaning that the sphere has rotational symmetry. Each rotation is prescribed by the latitude and longitude where the axis cuts the southern hemisphere, and by an angle through which it rotates the sphere. 1 These three parameters specify all rotations of the sphere, which thus has three-dimensional rotational symmetry. In general, a symmetry may be viewed as being a transformation (such as a rotation) that leaves an object looking unchanged. When one transformation is followed by a second, the result is a third transformation that is called the product of the other two. The collection of symmetries and their product 1 Note that we include the rotation through the angle 0, that is, the case where the globe actually does not rotate at all. 1 operation forms an algebraic structure called a group 2 . -

Line Geometry for 3D Shape Understanding and Reconstruction
Line Geometry for 3D Shape Understanding and Reconstruction Helmut Pottmann, Michael Hofer, Boris Odehnal, and Johannes Wallner Technische UniversitÄat Wien, A 1040 Wien, Austria. fpottmann,hofer,odehnal,[email protected] Abstract. We understand and reconstruct special surfaces from 3D data with line geometry methods. Based on estimated surface normals we use approximation techniques in line space to recognize and reconstruct rotational, helical, developable and other surfaces, which are character- ized by the con¯guration of locally intersecting surface normals. For the computational solution we use a modi¯ed version of the Klein model of line space. Obvious applications of these methods lie in Reverse Engi- neering. We have tested our algorithms on real world data obtained from objects as antique pottery, gear wheels, and a surface of the ankle joint. Introduction The geometric viewpoint turned out to be highly successful in dealing with a variety of problems in Computer Vision (see, e.g., [3, 6, 9, 15]). So far mainly methods of analytic geometry (projective, a±ne and Euclidean) and di®erential geometry have been used. The present paper suggests to employ line geometry as a tool which is both interesting and applicable to a number of problems in Computer Vision. Relations between vision and line geometry are not entirely new. Recent research on generalized cameras involves sets of projection rays which are more general than just bundles [1, 7, 18, 22]. A beautiful exposition of the close connections of this research area with line geometry has recently been given by T. Pajdla [17]. The present paper deals with the problem of understanding and reconstruct- ing 3D shapes from 3D data. -

Mel's 2019 Fishing Line Diameter Page
Welcome to Mel's 2019 Fishing Line Diameter page The line diameter tables below offer a comparison of more than 115 popular monofilament, copolymer, fluorocarbon fishing lines and braided superlines in tests from 6-pounds to 600-pounds If you like what you see, download a copy You can also visit our Fishing Line Page for more information and links to line manufacturers. The line diameters shown are compiled from manufacturer's web sites, product catalogs and labels on line spools. Background Information When selecting a fishing line, one must consider a number of factors. While knot strength, abrasion resistance, suppleness, shock resistance, castability, stretch and low spool memory are all important characteristics, the diameter of a line is probably the most important. As long as these other characteristics meet your satisfaction, then the smaller the diameter of the line the better. With smaller diameter lines: more line can be spooled onto the reel, they are usually less visible to the fish, will generally cast better, and provide better lure action. Line diameter measurements provided by manufacturers are expressed in thousandths of an inch (0.001 inch) and its metric system equivalent, hundredths of a millimeter (0.01 mm). However, not all manufacturers provide line diameter information, so if you don't see it in the tables, that's the likely reason why. And some manufacturers now provide line diameter measurements in ten-thousandths of an inch (0.0001 inch) and thousandths of a millimeter (0.001 mm). To give you an idea of just how small this is, one ten-thousandth of an inch is less than 3% of the diameter of an average human hair. -
Creating a Revolve
Always begin your creo session by selecting your working directory If you select working directory at the beginning, that folder will be the default location when you try to open files, as well as when you save files. It makes everything a lot easier if you select your working directory first. For help opening/saving/downloading files see basics, for help creating an extrude see basic solids. Creating a Revolve Open a new part file, name it something unique. Choose a plane to sketch on Go to sketch view (if you don’t know where that is see Basic Solids) Move your cursor so the centerline snaps to the horizontal line as shown above You may now begin your sketch I have just sketched a random shape Sketch Tips: ● Your shape MUST be closed ● If you didn’t put a centerline in, you will get radial instead of diameter dimensions (in general this is bad) ● Remember this is being revolved so you are only sketching the profile on one side of the center line. If you need to put in diameter dimensions: Click normal, click the line or point you want the dimension for, click the centerline, and click the same line/point that you clicked the first time AGAIN, and then middle mouse button where you want the dimension to be placed. After your sketch is done, click the checkmark to get out of sketch, then click the checkmark again to complete the revolve The part in the sketch will look like this: .