DOCSLIB.ORG

8-Bit 0 D1 Load Reg1 a 4×1 O • Ch2 Example: Four A0 V

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
8-Bit 0 D1 Load Reg1 a 4×1 O • Ch2 Example: Four A0 V Digital Design Chapter 4: Datapath Components Digital Design Copyright © 2006 1 Frank Vahid 4.1 Introduction • Chapters 2 & 3: Introduced increasingly complex digital building blocks – Gates, multiplexors, decoders, basic registers, and controllers • Controllers good for systems with control inputs/outputs – Control input: Single bit (or just a few), representing environment event or state • e.g., 1 bit representing button pressed – Data input: Multiple bits collectively representing single entity si • e.g., 7 bits representing temperature in binary ansis • Need building blocks for data – Datapath components, aka register-transfer-level (RTL) components, e store/transform data z • Put datapath components together to form a datapath • This chapter introduces numerous datapath components, and simple datapaths – Next chapter will combine controllers and datapaths into “processors” Digital Design Copyright © 2006 2 Frank Vahid 4.2 Registers b x • Can store data, very common in datapaths Combinational n1 logic • Basic register of Ch 3: Loaded every cycle n0 s1 s0 – Useful for implementing FSM -- stores encoded state clk State register – For other uses, may want to load only on certain cycles a load I3 I2 I1 I0 4-bit register I3 I2 I1 I0 D D D D si Q Q Q Q ansis reg(4) clk Q3 Q2 Q1 Q0 e Q3 Q2 Q1 Q0 z Basic register loads on every clock cycle How extend to only load on certain cycles? Digital Design Copyright © 2006 3 Frank Vahid Register with Parallel Load • Add 2x1 mux to front of each flip-flop • Register’s load input selects mux input to pass – Either existing flip-flop value, or new value to load I3 I2 I1 I0 10 10 10 10 load 2⋅ 1 I3 I2 I1 I0 load D D D D Q3 Q2 Q1 Q0 Q Q Q Q Q3 Q2 Q1 Q0 (a) (c) I3 I2 I1 I0 I3 I2 I1 I0 0 1 = 10 10 10 10 = 10 10 10 10 d d a a lo lo D D D D D D D D Q Q Q Q Q Q Q Q Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0 Digital Design (b) Copyright © 2006 4 Frank Vahid Basic Example Using Registers a3 a2 a1 a0 I3 I2 I1 I0 • This example will show how 1 ld clk R0 registers load simultaneously Q3 Q2 Q1 Q0 on clock cycles – Notice that all load inputs set to 1 in this example -- just for demonstration purposes 1 ld I3 I2 I1 I0 1 ld I3 I2 I1 I0 R1 R2 Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0 Digital Design Copyright © 2006 5 Frank Vahid Basic Example Using Registers clk n 12345 (a) e v gi a3..a0 1111 0001 1010 R0 ???? 1111 0001 1010 1010 1010 R1 ???? ???? 1111 0001 1010 1010 R2 ???? ???? 0000 1110 0101 0101 –>1111 1111–>0001 0001–>1010 1010 1010 1010 a3 a2 a1 a0 1 ld I3 I2 I1 I0 ???? R0 1111 R0 0001 R0 1010 R0 1010 R0 1010 R0 clk R0 Q3 Q2 Q1 Q0 (b) ???? ???? ???? ???? 1111 0000 0001 1110 1010 0101 1010 0101 R1 R2 R1 R2 R1 R2 R1 R2 R1 R2 R1 R2 1 ld I3 I2 I1 I0 1 ld I3 I2 I1 I0 R1 R2 Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0 Digital Design Copyright © 2006 6 Frank Vahid Register Example using the Load Input: Weight Sampler • Scale has two displays – Present weight – Saved weight Scale Weight Sampler – Useful to compare 00110010 present item with previous Save item b 1 I3 I2 I1 I0 a 32 pounds load 0011 • Use register to store Present weight clk Q3 Q2 Q1 Q0 weight – Pressing button causes present weight to be 3 pounds stored in register Saved weight • Register contents always displayed as “Saved weight,” even when new present weight appears Digital Design Copyright © 2006 7 Frank Vahid Register Example: Temperature History Display • Recall Chpt 3 example – Timer pulse every hour – Previously used as clock. Better design only connects oscillator to clock inputs -- use registers with load input, connect to timer pulse. a4 a3 a2 a1 a0 b4 b3 b2 b1 b0 c4 c3 c2 c1 c0 a4 a3 a2 a1 a0 b4 b3 b2 b1 b0 c4 c3 c2 c1 c0 I4 Q4 I4 Q4 I4 Q4 t4 I4 Q4 I4 Q4 I4 Q4 x4 I3 Q3 I3 Q3 I3 Q3 t3 I3 Q3 I3 Q3 I3 Q3 x3 I2 Q2 I2 Q2 I2 Q2 t2 I2 Ra Q2 I2 RbQ2 I2 RcQ2 x2 I1 Q1 I1 Q1 I1 Q1 t1 I1 Q1 I1 Q1 I1 Q1 x1 I0 Q0 I0 Q0 I0 Q0 t0 I0 Q0 I0 Q0 I0 Q0 x0 ld ld ld Clk Ra Rb Rc osc C C TemperatureHistoryStorage a timer new line TemperatureHistoryStorage Digital Design Copyright © 2006 8 Frank Vahid Register Example: Above-Mirror Display 8 Shorthand notation a 0001010 er C t 8 Loaded on clock edge d0 load reg0 T ompu mi T c o theab r al i0 r r 2⋅ 4 or displ t omthe car's r n 8 F e c 1 8-bit 0 d1 load reg1 A 4×1 o • Ch2 example: Four a0 v a 0001010 e i0 y simultaneous values from i1 car’s computer 1 i1 8 a1 d D • To reduce wires: Computer d2 load reg2 I 8 writes only 1 value at a time, i2 loads into one of four 8 registers d3 load e reg3 M – Was: 8+8+8+8 = 32 wires 1 load i3 s1 s0 – Now: 8 +2+1 = 11 wires 8 Digital Design xy Copyright © 2006 9 Frank Vahid Register Example: Computerized Checkerboard • Each register LED lit LED holds values for 1 one column of 0 lights 1 – 1 lights light 0 • Microprocessor loads one 0 register at a time 0 – Occurs fast 1 enough that 0 user sees Q R7 R6 R5 R4 R3 R2 R1 R0 R0 10100010 entire board I load change at once d7 d6 d5 d4 d3 d2 d1 d0 8 ei2i1i03⋅ 8 decoder from from microprocessor decoder D (b) microprocessor Digital Design (a) Copyright © 2006 10 Frank Vahid Register Example: Computerized Checkerboard LED lit LED R7 R6 R5 R4 R3 R2 R1 R0 10100010 10100010 10100010 10100010 01000101 01000101 01000101 01000101 D 10100010 010000101 10100010 010000101 10100010 010000101 10100010 010000101 i2,i1,i0 000 (R0) 001 (R1) 010 (R2) 011 (R3) 100 (R4) 101 (R5) 110 (R6) 111 (R7) e clk Digital Design Copyright © 2006 11 Frank Vahid Shift Register Register contents 1 1 0 1 before shift right • Shift right 0 a Register contents – Move each bit one position right 0 1 1 0 after shift right – Shift in 0 to leftmost bit Q: Do four right shifts on 1001, showing value after each shift a A: 1001 (original) 0100 • Implementation: Connect flip-flop 0010 output to next flip-flop’s input 0001 shr_in a 0000 Digital Design Copyright © 2006 12 Frank Vahid Shift Register • To allow register to either shift or retain, use 2x1 muxes – shr: 0 means retain, 1 shift – shr_in: value to shift in • May be 0, or 1 • Note: Can easily design shift register that shifts left instead shr_in 1 shr 10 10 10 10 = 10 10 10 10 r 2⋅ 1 2⋅ 1 sh D D D D D D D D Q Q Q Q Q Q Q Q Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0 (b) (a) shr_in shr Q3 Q2 Q1 Q0 Digital Design Copyright © 2006 (c) 13 Frank Vahid Rotate Register Register contents 1 1 0 1 before shift right • Rotate right: Like shift right, Register contents 1 1 1 0 but leftmost bit comes from after shift right rightmost bit Digital Design Copyright © 2006 14 Frank Vahid Shift Register Example: Above-Mirror Display r s e C s t ' 8 r a e c d0 load e reg0 T ompu h r mi To c l i r t • Earlier example: 8 a i0 r r or 2⋅ 4 h t om t r 8 e n di F e 8-bit a c b w d1 load s p reg1 A 4⋅ 1 o l a0 v a +2+1 = 11wires from e i0 y 1 i1 i1 8 1 a1 d D car’s computer to d2 load reg2 I 8 i2 8 above-mirror display’s d3 load e reg3 M load i3 four registers 8 s1 s0 xy – Better than 32 wires, Note: this line is 1 bit, rather than 8 bits like before but 11 still a lot -- c xy want fewer for shr_in d0 shr reg0 T smaller wire bundles s1 s0 2⋅ 4 i0 • Use shift registers 8 shr_in 4×1 – Wires: 1+2+1=4 d1 shr reg1 A a0 i0 – Computer sends one i1 a1 i1 8 value at a time, one shr_in d D d2 shr reg2 I 8 bit per clock cycle i2 8 shr_in shr e d3 reg3 M Digital Design shift i3 Copyright © 2006 8 15 Frank Vahid Multifunction Registers • Many registers have multiple functions – Load, shift, clear (load all 0s) – And retain present value, of course Functions: • Easily designed using muxes s1 s0 Operation – Just connect each mux input to achieve 0 0 Maintain present value 0 1 Parallel load desired function 1 0 Shift right 1 1 (unused - let's load 0s) shr_in I3 I2 I1 I0 0 0 0 0 s1 3210 3210 3210 3210 s0 4⋅ 1 shr_in I3 I2 I1 I0 s1 D D D D s0 Q3 Q2 Q1 Q0 Q Q Q Q Q3 Q2 Q1 Q0 (b) (a) Digital Design Copyright © 2006 16 Frank Vahid Multifunction Registers s1 s0 Operation 0 0 Maintain present value 0 1 Parallel load 1 0 Shift right 1 1 Shift left I3 I2 I1 I0 shr_in shl_in 3210 3210 3210 3210 shl_in I3 I2 I1 I0 shr_in D D D D s1 s0 Q Q Q Q Q3 Q2 Q1 Q0 Q3 Q2 Q1 Q0 (a) (b) Digital Design Copyright © 2006 17 Frank Vahid Multifunction Registers with Separate Control Inputs ld shr shl Operation 0 0 0 Maintain present value 0 0 1 Shift left 0 1 0 Shift right 0 1 1 Shift right – shr has priority over shl 1 0 0 Parallel load 1 0 1 Parallel load – ld has priority I3 I2 I1 I0 1 1 0 Parallel load – ld has priority shr_in 1 1 1 Parallel load – ld has priority ld shr_in I3 I2 I1 I0 s1 shl_in combi- shl_in shr national s0 Truth table for combinational circuit circuit shl Q3 Q2 Q1 Q0 Inputs Outputs Note ? ld shr shl s1 s0 Operation Q3 Q2 Q1 Q0 0 0 0 0 0 Maintain value 1 1 Shift left 0 0 1 a 0 1 0 1 0 Shift right 0 1 1 1 0 Shift right 1 0 0 0 1 Parallel load s1 = ld’*shr’*shl + ld’*shr*shl’ + ld’*shr*shl 1 0 1 0 1 Parallel load 1 1 0 0 1 Parallel load s0 = ld’*shr’*shl + ld a 1 1 1 0 1 Parallel load a Digital Design Copyright © 2006 18 Frank Vahid Register Operation Table • Register operations typically shown using compact version of table – X means same operation whether value is 0 or 1 • One X expands to two rows • Two Xs expand to four rows – Put highest priority control input on left to make reduced table simple Inputs Outputs Note ld shr shl s1 s0 Operation ld shr shl Operation 0 0 0 0 0 Maintain value 0 0 0 Maintainvalue 0 0 1 1 1 Shift left 0 0 1 Shift left 0 1 0 1 0 Shift right 0 1 X Shift right 0 1 1 1 0 Shift right 1 X X Parallel load 1 0 0 0 1 Parallel load 1 0 1 0 1 Parallel load 1 1 0 0 1 Parallel load 1 1 1 0 1 Parallel load Digital Design Copyright © 2006 19 Frank Vahid Register Design Process • Can design register with desired operations using
Load more

Recommended publications
  • Implementation of Optimized CORDIC Designs
    IJIRST –International Journal for Innovative Research in Science & Technology| Volume 1 | Issue 3 | August 2014 ISSN(online) : 2349-6010 Implementation of Optimized CORDIC Designs Bibinu Jacob Reenesh Zacharia M Tech Student Assistant Professor Department of Electronics & Communication Engineering Department of Electronics & Communication Engineering Mangalam College Of Engineering, Ettumanoor Mangalam College Of Engineering, Ettumanoor Abstract CORDIC stands for COordinate Rotation DIgital Computer, which is likewise known as Volder's algorithm and digit-by-digit method. It is a simple and effective method to calculate many functions like trigonometric, hyperbolic, logarithmic etc. It performs complex multiplications using simple shifts and additions. It finds applications in robotics, digital signal processing, graphics, games, and animation. But, there isn't any optimized CORDIC designs for rotating vectors through specific angles. In this paper, optimization schemes and CORDIC circuits for fixed and known rotations are proposed. Finally an argument reduction technique to map larger angle to an angle less than 45 is discussed. The proposed CORDIC cells are simulated by Xilinx ISE Design Suite and shown that the proposed designs offer less latency and better device utilization than the reference CORDIC design for fixed and known angles of rotation. Keywords: Coordinate rotation digital computer (CORDIC), digital signal processing (DSP) chip, very large scale integration (VLSI) _______________________________________________________________________________________________________ I. INTRODUCTION The advances in the very large scale integration (VLSI) technology and the advent of electronic design automation (EDA) tools have been directing the current research in the areas of digital signal processing (DSP), communications, etc. in terms of the design of high speed VLSI architectures for real-time algorithms and systems which have applications in the above mentioned areas.
    [Show full text]
  • Binary Counter
    Systems I: Computer Organization and Architecture Lecture 8: Registers and Counters Registers • A register is a group of flip-flops. – Each flip-flop stores one bit of data; n flip-flops are required to store n bits of data. – There are several different types of registers available commercially. – The simplest design is a register consisting only of flip- flops, with no other gates in the circuit. • Loading the register – transfer of new data into the register. • The flip-flops share a common clock pulse (frequently using a buffer to reduce power requirements). • Output could be sampled at any time. • Clearing the flip-flop (placing zeroes in all its bit) can be done through a special terminal on the flip-flop. 1 4-bit Register I0 D Q A0 Clock C I1 D Q A1 C I D Q 2 A2 C D Q A I3 3 C Clear Registers With Parallel Load • The clock usually provides a steady stream of pulses which are applied to all flip-flops in the system. • A separate control system is needed to determine when to load a particular register. • The Register with Parallel Load has a separate load input. – When it is cleared, the register receives it output as input. – When it is set, it received the load input. 2 4-bit Register With Parallel Load Load D Q A0 I0 C D Q A1 C I1 D Q A2 I2 C D Q A3 I3 C Clock Shift Registers • A shift register is a register which can shift its data in one or both directions.
    [Show full text]
  • Master's Thesis
    Implementation of the Metal Privileged Architecture by Fatemeh Hassani A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Masters of Mathematics in Computer Science Waterloo, Ontario, Canada, 2020 c Fatemeh Hassani 2020 Author's Declaration I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract The privileged architecture of modern computer architectures is expanded through new architectural features that are implemented in hardware or through instruction set extensions. These extensions are tied to particular architecture and operating system developers are not able to customize the privileged mechanisms. As a result, they have to work around fixed abstractions provided by processor vendors to implement desired functionalities. Programmable approaches such as PALcode also remain heavily tied to the hardware and modifying the privileged architecture has to be done by the processor manufacturer. To accelerate operating system development and enable rapid prototyping of new operating system designs and features, we need to rethink the privileged architecture design. We present a new abstraction called Metal that enables extensions to the architecture by the operating system. It provides system developers with a general-purpose and easy- to-use interface to build a variety of facilities that range from performance measurements to novel privilege models. We implement a simplified version of the Alpha architecture which we call µAlpha and build a prototype of Metal on this architecture.
    [Show full text]
  • Cross Architectural Power Modelling
    Cross Architectural Power Modelling Kai Chen1, Peter Kilpatrick1, Dimitrios S. Nikolopoulos2, and Blesson Varghese1 1Queen’s University Belfast, UK; 2Virginia Tech, USA E-mail: [email protected]; [email protected]; [email protected]; [email protected] Abstract—Existing power modelling research focuses on the processor are extensively explored using a cumbersome trial model rather than the process for developing models. An auto- and error approach after which a suitable few are selected [7]. mated power modelling process that can be deployed on different Such an approach does not easily scale for various processor processors for developing power models with high accuracy is developed. For this, (i) an automated hardware performance architectures since a different set of hardware counters will be counter selection method that selects counters best correlated to required to model power for each processor. power on both ARM and Intel processors, (ii) a noise filter based Currently, there is little research that develops automated on clustering that can reduce the mean error in power models, and (iii) a two stage power model that surmounts challenges in methods for selecting hardware counters to capture proces- using existing power models across multiple architectures are sor power over multiple processor architectures. Automated proposed and developed. The key results are: (i) the automated methods are required for easily building power models for a hardware performance counter selection method achieves compa- collection of heterogeneous processors as seen in traditional rable selection to the manual method reported in the literature, data centers that host multiple generations of server proces- (ii) the noise filter reduces the mean error in power models by up to 55%, and (iii) the two stage power model can predict sors, or in emerging distributed computing environments like dynamic power with less than 8% error on both ARM and Intel fog/edge computing [8] and mobile cloud computing (in these processors, which is an improvement over classic models.
    [Show full text]
  • Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R
    et International Journal on Emerging Technologies 11 (2): 668-673(2020) ISSN No. (Print): 0975-8364 ISSN No. (Online): 2249-3255 Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R. Venkata Siva Reddy 2 1Research Scholar, VTU Belagavi (Karnataka), India. 2School of Electronics and Communication Engineering, REVA University Bengaluru, (Karnataka), India. (Corresponding author: Amrut Anilrao Purohit) (Received 04 January 2020, Revised 02 March 2020, Accepted 03 March 2020) (Published by Research Trend, Website: www.researchtrend.net) ABSTRACT: Arithmetic and Logic Unit (ALU) can be understood with basic knowledge of digital electronics and any engineer will go through the details only once. The advantage of knowing ALU in detail is two- folded: firstly, programming of the processing device can be efficient and secondly, can design a new ALU architecture as per the various constraints of the use cases. The miniaturization of digital circuits can be achieved by either reducing the size of transistor (Moore’s law) or by optimizing the gate count of the circuit. The first has been explored extensively while the latter has been ignored which deals with the application of Boolean rules and requires sound knowledge of logic design. The ultimate outcome is to have an area optimized architecture/approach that optimizes the circuit at gate level. The design of ALU is for various processing devices varies with the device/system requirements. The area optimization places a significant role in the chip design. Here in this work, we have attempted to design an ALU which is area efficient while being loaded with additional functionality necessary for microcontrollers.
    [Show full text]
  • Experiment No
    1 LIST OF EXPERIMENTS 1. Study of logic gates. 2. Design and implementation of adders and subtractors using logic gates. 3. Design and implementation of code converters using logic gates. 4. Design and implementation of 4-bit binary adder/subtractor and BCD adder using IC 7483. 5. Design and implementation of 2-bit magnitude comparator using logic gates, 8- bit magnitude comparator using IC 7485. 6. Design and implementation of 16-bit odd/even parity checker/ generator using IC 74180. 7. Design and implementation of multiplexer and demultiplexer using logic gates and study of IC 74150 and IC 74154. 8. Design and implementation of encoder and decoder using logic gates and study of IC 7445 and IC 74147. 9. Construction and verification of 4-bit ripple counter and Mod-10/Mod-12 ripple counter. 10. Design and implementation of 3-bit synchronous up/down counter. 11. Implementation of SISO, SIPO, PISO and PIPO shift registers using flip-flops. KCTCET/2016-17/Odd/3rd/ETE/CSE/LM 2 EXPERIMENT NO. 01 STUDY OF LOGIC GATES AIM: To study about logic gates and verify their truth tables. APPARATUS REQUIRED: SL No. COMPONENT SPECIFICATION QTY 1. AND GATE IC 7408 1 2. OR GATE IC 7432 1 3. NOT GATE IC 7404 1 4. NAND GATE 2 I/P IC 7400 1 5. NOR GATE IC 7402 1 6. X-OR GATE IC 7486 1 7. NAND GATE 3 I/P IC 7410 1 8. IC TRAINER KIT - 1 9. PATCH CORD - 14 THEORY: Circuit that takes the logical decision and the process are called logic gates.
    [Show full text]
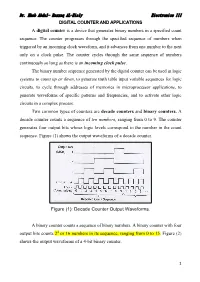
  • 1 DIGITAL COUNTER and APPLICATIONS a Digital Counter Is
    Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III DIGITAL COUNTER AND APPLICATIONS A digital counter is a device that generates binary numbers in a specified count sequence. The counter progresses through the specified sequence of numbers when triggered by an incoming clock waveform, and it advances from one number to the next only on a clock pulse. The counter cycles through the same sequence of numbers continuously so long as there is an incoming clock pulse. The binary number sequence generated by the digital counter can be used in logic systems to count up or down, to generate truth table input variable sequences for logic circuits, to cycle through addresses of memories in microprocessor applications, to generate waveforms of specific patterns and frequencies, and to activate other logic circuits in a complex process. Two common types of counters are decade counters and binary counters. A decade counter counts a sequence of ten numbers, ranging from 0 to 9. The counter generates four output bits whose logic levels correspond to the number in the count sequence. Figure (1) shows the output waveforms of a decade counter. Figure (1): Decade Counter Output Waveforms. A binary counter counts a sequence of binary numbers. A binary counter with four output bits counts 24 or 16 numbers in its sequence, ranging from 0 to 15. Figure (2) shows-the output waveforms of a 4-bit binary counter. 1 Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III Figure (2): Binary Counter Output Waveforms. EXAMPLE (1): Decade Counter. Problem: Determine the 4-bit decade counter output that corresponds to the waveforms shown in Figure (1).
    [Show full text]
  • Design and Implementation of High Speed Counters Using “MUX Based Full Adder (MFA)”
    IOSR Journal of Electronics and Communication Engineering (IOSR-JECE) e-ISSN: 2278-2834,p- ISSN: 2278-8735.Volume 14, Issue 4, Ser. I (Jul.-Aug. 2019), PP 57-64 www.iosrjournals.org Design and Implementation of High speed counters using “MUX based Full Adder (MFA)” K.V.Jyothi1, G.P.S. Prashanti2, 1Student, 2Assistant Professor 1,2,(Department of Electronics and Communication Engineering, Gayatri Vidya Parishad College of Engineering For Women,Visakhapatnam, Andhra Pradesh, India) Corresponding Author: K.V.Jyothi Abstract: In this brief, a new binary counter design is proposed. Counters are used to determine how many number of inputs are active (in the logic ONE state) for multi input circuits. In the existing systems 6:3 and 7:3 Counters are designed with full and half adders, parallel counters, stacking circuits. It uses 3-bit stacking and 6-bit stacking circuits which group all the “1” bits together and then stacks are converted into binary counts. This leads to increase in delay and area. To overcome this problem “MUX based Full adder (MFA)” 6:3 and 7:3 counters are proposed. The backend counter simulations are achieved by using MENTOR GRAPHICS in 130nm technology and frontend simulations are done by using XILINX. This MFA counter is faster than existing stacking counters and also consumesless area. Additionally, using this counters in Wallace tree multiplier architectures reduces latency for 64 and 128-bit multipliers. Keywords: stacking circuits, parallel counters,High speed counters, MUX based full adder (MFA) counter,Mentor graphics,Xilinx,SPARTAN-6 FPGA. ----------------------------------------------------------------------------------------------------------------------------- ---------- Date of Submission: 28-07-2019 Date of acceptance: 13-08-2019 ----------------------------------------------------------------------------------------------------------------------------- ---------- I.
    [Show full text]
  • Hardware-Assisted Rootkits: Abusing Performance Counters on the ARM and X86 Architectures
    Hardware-Assisted Rootkits: Abusing Performance Counters on the ARM and x86 Architectures Matt Spisak Endgame, Inc. [email protected] Abstract the OS. With KPP in place, attackers are often forced to move malicious code to less privileged user-mode, to ele- In this paper, a novel hardware-assisted rootkit is intro- vate privileges enabling a hypervisor or TrustZone based duced, which leverages the performance monitoring unit rootkit, or to become more creative in their approach to (PMU) of a CPU. By configuring hardware performance achieving a kernel mode rootkit. counters to count specific architectural events, this re- Early advances in rootkit design focused on low-level search effort proves it is possible to transparently trap hooks to system calls and interrupts within the kernel. system calls and other interrupts driven entirely by the With the introduction of hardware virtualization exten- PMU. This offers an attacker the opportunity to redirect sions, hypervisor based rootkits became a popular area control flow to malicious code without requiring modifi- of study allowing malicious code to run underneath a cations to a kernel image. guest operating system [4, 5]. Another class of OS ag- The approach is demonstrated as a kernel-mode nostic rootkits also emerged that run in System Manage- rootkit on both the ARM and Intel x86-64 architectures ment Mode (SMM) on x86 [6] or within ARM Trust- that is capable of intercepting system calls while evad- Zone [7]. The latter two categories, which leverage vir- ing current kernel patch protection implementations such tualization extensions, SMM on x86, and security exten- as PatchGuard.
    [Show full text]
  • 8-Bit Barrel Shifter That May Rotate the Data in Both Direction
    © 2018 IJRAR December 2018, Volume 5, Issue 04 www.ijrar.org (E-ISSN 2348-1269, P- ISSN 2349-5138) Performance Analysis of Low Power CMOS based 8 bit Barrel Shifter Deepti Shakya M-Tech VLSI Design SRCEM Gwalior (M.P) INDIA Shweta Agrawal Assistant Professor, Dept. Electronics & Communication Engineering SRCEM Gwalior (M.P), INDIA Abstract Barrel Shifter isimportant function to optimize the RISC processor, so it is used for rotating and transferring the data either in left or right direction. This shifter is useful in lots of signal processing ICs. The Arithmetic and the Logical Shifters additionally can be changed by the Barrel Shifter Because with the rotation of the data it also supply the utility the data right, left changeall mathemetically or logically.A purpose of this paper is to design the CMOS 8 bit barrel shifter using universal gates with the help of CMOS logic and the most important 2:1 multiplexers (MUX). CMOS based 8 bit barrel shifter has implemented in this paper and compared in terms of delay and power using 90 nm and 45nm technologies. Key Words: CMOS, Low Power, Delay,Barrel Shifter, PMOS, NMOS, Cadence. 1. Introduction In RISC processor ALU plays math and intellectual operations. Number crunching operations operate enlargement, subtraction, addition and division such as sensible operations incorporates AND, OR, NOT, NAND, NOR, XNOR and XOR. RISC processor consist ofnotice in credentials used to keep the operand in store path. The point of control unit is to give a control flag that controls the operation of the processor which tells the small scale building design which operation is done after then the time Barrel shifter is a significant element among rise operation.
    [Show full text]
  • A Lisp Oriented Architecture by John W.F
    A Lisp Oriented Architecture by John W.F. McClain Submitted to the Department of Electrical Engineering and Computer Science in partial fulfillment of the requirements for the degrees of Master of Science in Electrical Engineering and Computer Science and Bachelor of Science in Electrical Engineering at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY September 1994 © John W.F. McClain, 1994 The author hereby grants to MIT permission to reproduce and to distribute copies of this thesis document in whole or in part. Signature of Author ...... ;......................... .............. Department of Electrical Engineering and Computer Science August 5th, 1994 Certified by....... ......... ... ...... Th nas F. Knight Jr. Principal Research Scientist 1,,IA £ . Thesis Supervisor Accepted by ....................... 3Frederic R. Morgenthaler Chairman, Depattee, on Graduate Students J 'FROM e ;; "N MfLIT oARIES ..- A Lisp Oriented Architecture by John W.F. McClain Submitted to the Department of Electrical Engineering and Computer Science on August 5th, 1994, in partial fulfillment of the requirements for the degrees of Master of Science in Electrical Engineering and Computer Science and Bachelor of Science in Electrical Engineering Abstract In this thesis I describe LOOP, a new architecture for the efficient execution of pro- grams written in Lisp like languages. LOOP allows Lisp programs to run at high speed without sacrificing safety or ease of programming. LOOP is a 64 bit, long in- struction word architecture with support for generic arithmetic, 64 bit tagged IEEE floats, low cost fine grained read and write barriers, and fast traps. I make estimates for how much these Lisp specific features cost and how much they may speed up the execution of programs written in Lisp.
    [Show full text]
  • 4-Bit Barrel Shifter Using Transmission Gates
    4-BIT BARREL SHIFTER USING TRANSMISSION GATES M.Muralikrishna1, Nadikuda yadagiri2, GuntupallySai chaitanya3, PalugulaPranay Reddy4 1ECE, Assistant Professor, Anurag Group of Institutions/JNTU University, Hyderabad 2, 3, 4ECE, Anurag Group of Institutions/JNTU University, Hyderabad Abstract In Arithmetic shifter the procedure for Barrel shifter plays an important role in the left shifting is same as logical but in case of floating point arithmetic operations and right shifting the empty spot is filled by signed optimizing the RISC processor and used for bit. Funnel Shifter is combination of all shifters rotating andshifting the data either in left or and rotator In this paper barrel shifter is right direction. This shifter is useful in many designed using multiplexer and implemented signal processing ICs. The arithmetic and using CMOS logic.The MUX used is made with logical shifter are itself a type of barrel the help of universal gates so that the time delay shifter. The main objective of this paper is to and power dissipation is reduced. design a fully custom two bit barrel shifter using 4x1 multiplexer with the help of II. BARREL SHIFTER transmission gates and analyze the A barrel shifter is a digital circuit that can performance on basis of power consumption, shift a data word by a specified number of bits and no of transistors. The tool used to fulfill without the use of any sequential logic, only the purpose is cadence virtuoso using 180nm pure combinatorial logic. One way to technology. implement it is as a sequence of multiplexers Keywords: Barrel shifter, Transmission where the output of one multiplexer is gates, Multiplexer connected to the input of the next multiplexer in a way that depends on the shift distance.
    [Show full text]