DOCSLIB.ORG

Boyd University of Ottawa University of Rochester University of Glasgow

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Boyd University of Ottawa University of Rochester University of Glasgow Introduction to Nonlinear Optics Robert W. Boyd University of Ottawa University of Rochester University of Glasgow P resented at the International School of Physics “Enrico Fermi,” Course 190 - Frontiers in Modern Optics, 30 June - 5 July, 2014. Outline of Presentation Part I. Tutorial Introduction to Nonlinear Optics Part II. Recent Research in Quantum Nonlinear Optics Why Study Nonlinear Optics? It is good fundamental physics. It leads to important applications. It is a lot of fun. Demonstrate these features with examples in remainder of talk. 1. What is Nonlinear Optics? Nonlinear Optics and Light-by-Light Scattering The elementary process of light-by-light scattering has never been observed in vacuum, but is readily observed using the nonlinear response of material systems. Nonlinear material is fluorescein-doped boric acid glass (FBAG) 14 n2 n2(silica) [But very slow response!] M. A. Kramer, W. R. Tompkin, and R. W. Boyd, Phys. Rev. A, 34, 2026, 1986. W. R. Tompkin, M. S. Malcuit, and R. W. Boyd, Applied Optics 29, 3921, 1990. Opomjofbs!Pqujdt UIJSE!FEJUJPO Spcfsu!X/!Cpze Some Fundamental Nonlinear Optical Processes: I Second-Harmonic Generation 2 (2) 2 Dolgaleva, Lepeshkin, and Boyd Some Fundamental Nonlinear Optical Processes: II Sum-Frequency Generation 1 = + 2 (2) 3 1 2 2 3 1 Some Fundamental Nonlinear Optical Processes: III Difference-Frequency Generation amplified! 1 = 3 1 2 2 (2) 1 2 3 Optical Parametric Oscillation Parametric Downconversion: A Source of Entangled Photons The signal and idler photons are entangled in: (a) polarization (b) time and energy (c) position and transverse momentum (d) angular position and orbital angular momentum Entanglement is important for: (a) Fundamental tests of QM (e.g., nonlocality) (a) Quantum technologies (e.g., secure communications) Some Fundamental Nonlinear Optical Processes: III Third-Harmonic Generation (3) 3 3 Some Fundamental Nonlinear Optical Processes: IV Intensity-Dependent Index of Refraction i E( ) E( ) e NL self-phase modulation (3) cross-phase modulation E( ) (strong wave) i (3) NL E( ') E( ')e (probe wave) where Role of Material Symmetry in Nonlinear Optics (2) vanishes identically for a material possessing a center of inversion sym- metry (a centrosymmetric medium). non-centrosymmetric medium U(x) parabola parabola actual potential x centrosymmetric medium U(x) parabola parabola actual potential x 2. Coupled Wave Equations and Harmonic Generation Treatment of Second-Harmonic Generation – I z E ,ω E , 2ω 1 χ (2) 2 L Let i!t i(k z !t) E˜1(z,t)=E1(z)e− +c.c.=A1e 1 − +c.c. (1) i2!t i(k z 2!t) E˜2(z,t)=E2(z)e− +c.c.=A2(z)e 2 − +c.c. (2) where k1 = n1!/c and k2 = n22!/c. We have assumed that the pump wave E1 at frequency ! is unde- pleted by the nonlinear interaction. We take A2 to be a function of z to allow the second harmonic wave to grow with z.Wealsoset ˜ i2!t (2) 2 (2) 2 i2k1z P2(t)=P2 e− where P2 = ✏0χ E1 = ✏0χ A1 e (3) The generation of the wave at 2! is governed by the wave equation 2 2 ˜ 2 ˜ 2 ˜ n @ E2 1 @ P2 E2 2 2 = 2 2 . (4) r − c @t ✏0c @t Treatment of Second-Harmonic Generation – II Note that the first term in the wave equation is given by @2A˜ @A˜ 2 ˜ 2 2 2 2 3 i(k2z 2!t) E = 6 +2ik k A 7 e − (5) 2 6 2 2 2 27 6 7 r 6 @z @z − 7 6 7 4 5 @A˜ 2 2 2 3 i(k2z 2!t) 62ik k A 7 e (6) 6 2 2 27 − 6 7 ⇡ 6 @z − 7 6 7 The second form is the slowly4 varying amplitude5 approximation. Note also that @2A˜ @2P˜ 2 = (2!)2A ei(k2z 2!t) 2 = (2!)2P ei(2k1z 2!t) (7) @t2 − 2 − @t2 − 2 − By combining the above equations, we obtain dA 4!2 2ik 2 = − χ(2)A2ei∆kz where ∆k =2k k . (8) 2 dz c2 1 1 − 2 The quantity ∆k is known as the phase (or wavevector) mismatch factor, and it is crucially important in determining the efficiency of nonlinear optical interactions Treatment of Second-Harmonic Generation – III For the case ∆k =0,Eq.(8)becomes dA 4!2 2ik 2 = − χ(2)A2 (9) 2 dz c2 1 with solution evaluated at z = L of 2 2i! (2) 2 2 4! (2) 2 4 2 A2(L)= χ A1L or A2(L) = 2 2[χ ] A1 L . (10) n2c | | n2c | | Note that the SHG intensity scales as the square of the input intensity and also as the square of the length L of the crystal. 2ω 2ω dipole emitter phased array of dipoles Treatment of Second-Harmonic Generation – IV For the general case of ∆k =0,Eq.(8)canstillbesolvedtoyield 6 2 2 4! (2) 2 4 2 2 A2(L) = 2 2 [χ ] A1 L sinc (∆kL/2) (11) | | n2c | | Note that ∆kL must be kept much smaller than ⇡ radians in order for efficient SHG to occur. Second Harmonic Generation and Nonlinear Microscopy Nonlinear Optical Microscopy An important application of harmonic generation is nonlinear microscopy. Microscopy based on second-harmonic generation in the configuration of a confocal microscope and excited by femtosecond laser pulses was introduced by Curley et al. (1992). Also, harmonic-generation microscopy can be used to form images of transpar- ent (phase) objects, because the phase matching condition of nonlinear optics depends sensitively on the refractive index variation within the sample being imaged (Muller et al., 1998). Boyd, NLO, Subsection 2.7.1 Caution! Curley et al., not Curly et al. How to Achieve Phase Matching: Birefringence Phase Matching The phase matching condition ∆k =0requiresthat n ! n ! n ! 1 1 + 2 2 = 3 1 where ! + ! = ! c c c 1 2 3 These conditions are incompatible in an isotropic dispersive material. However, for a birefringent material phase matching can be achieved. cˆ ω θ 2ω k ordinary extraordinary Midwinter and Warner showed that there are two ways to achieve phase matching: Positive uniaxial Negative uniaxial (ne >n0)(ne <n0) 0 e e e o o Type I n3!3 = n1!1 + n2!2 n3!3 = n1!1 + n2!2 0 o e e e o Type II n3!3 = n1!1 + n2!2 n3!3 = n1!1 + n2!2 How to Achieve Phase Matching: Quasi Phase Matching single domain crystal periodically poled crystal Λ Sign of χ(2) is periodically inverted to prevent reverse power flow. (a) with perfect phase-matching (b) with quasi-phase-matching (c) with a wavevector mismatch field amplitude field 0 0 2 4 6 8 z / Lcoh Additional Studies of Wave Propagation Efects 3. Mechanisms of Optical Nonlinearity Typical Values of the Nonlinear Refractive Index a (3) n2 χ1111 Response time Mechanism (cm2/W) (m2/V2)(sec) 16 22 15 Electronic polarization 10− 10− 10− 14 20 12 Molecularorientation 10− 10− 10− 14 20 9 Electrostriction 10− 10− 10− 10 16 8 Saturated atomic absorption 10− 10− 10− 6 12 3 Thermal e↵ects 10− 10− 10− Photorefractive e↵ectb (large) (large) (intensity-dependent) a For linearly polarized light. b The photorefractive e↵ect often leads to a very strong nonlinear response. This response usually (3) cannot be described in terms of a χ (or an n2)nonlinearsusceptibility,becausethenonlinearpo- larization does not depend on the applied field strength in the same manner as the other mechanisms listed. Quantum Mechanical Origin of the Nonlinear Optical Suesceptibility ll l l (2) (! + ! ! ! ) ijk p q , q , p n n (a ) (a ) (a1) 1 2 i j k m m N (0) ω ln nm ml q ω p = 2 ll 2 0h [(!nl !p !q) i nl][(!ml !p) i ml] ω p lmn l l ω q ll i k j lnnmml + (a ) [(!nl !p !q) i nl][(!ml !q) i ml] 2 n n nn k i j lnnmml m m (a' ) + (a' ) 2 (a ) 1 [(!mn !p !q) i mn][(!nl + !p) + i nl] 1 ω q ω p j i k ω nm p ω q + ln ml ll ll [(! ! ! ) i ][(! + ! ) + i ] (a2) mn p q mn nl q nl j i k nn + ln nm ml nn (b1) [(!nm + !p + !q) + i nm][(!ml !p) i ml] (b ) 1 (b2) m m k i j ω q ω p lnnmml + ω ω [(! + ! + ! ) + i ][(! ! ) i ] (b2) p q nm p q nm ml q ml ll ll k j i lnnmml + (b ) [(!ml + !p + !q) + i ml][(!nl + !p) + i nl] 1 j k i mm mm lnnmml + b' ) (b2) 2 [(!ml + !p + !q) + i ml][(!nl + !q) + i nl] b' 1 n ω q n ω p ω p ω q l l ll Some Actual Z-Scan Data Closed aperture Open aperture 1.2 I0 = 0.176 GW/cm2 1.2 gold-silica composite CS 2 1.1 1.0 transmission 1.0 transmission n2 = Chang, Shin 0.0373 cm2/GW 0.8 Piredda 0.9 –20 0 20 z (mm) –125 0 125 z (mm) For closed aperture z-scan ΔTpv = 0.406 ΦNL where M. Sheik-Bahae et al., IEEE J. ΦNL = n2 (ω/c) Ι0 L Quantum Electron. 26 760 (1990). 6. Self-Action Effects in Nonlinear Optics Self-Action Efects in Nonlinear Optics Self-action efects: light beam modifes its own propagation tTFMGGPDVTJOH tTFMGUSBQQJOH d tTNBMMTDBMFöMBNFOUBUJPO Prediction of Self Trapping n = n0 d n = n0 +n n = n0 radial profle of self -trapped beam Optical Solitons Field distributions that propagate without change of form Temporal solitons (nonlinearity balances gvd) 1973: Hasegawa & Tappert 1980: Mollenauer, Stolen, Gordon Spatial solitons (nonlinearity balances difraction) 1964: Garmire, Chiao, Townes 1974: Ashkin and Bjorkholm (Na) 1985: Barthelemy, Froehly (CS2) 1991: Aitchison et al.
Load more

Recommended publications
  • Tutorial on Nonlinear Optics
    Proceedings of the International School of Physics “Enrico Fermi” Course 190 “Frontiers in Modern Optics”, edited by D. Faccio, J. Dudley and M. Clerici (IOS, Amsterdam; SIF, Bologna) 2016 DOI 10.3254/978-1-61499-647-7-31 Tutorial on nonlinear optics S. Choudhary School of Electrical Engineering and Computer Science, University of Ottawa Ottawa, Ontario, K1N 6N5 Canada R. W. Boyd School of Electrical Engineering and Computer Science, University of Ottawa Ottawa, Ontario, K1N 6N5 Canada The Institute of Optics, University of Rochester Rochester, New York, 14627 USA Department of Physics, University of Ottawa Ottawa, Ontario, K1N 6N5 Canada Summary. — Nonlinear optics deals with phenomena that occur when a very intense light interacts with a material medium, modifying its optical properties. Shortly after the demonstration of first working laser in 1960 by Maiman (Nature, 187 (1960) 493), the field of nonlinear optics began with the observation of second harmonic by Franken et al. in 1961 (Phys. Rev. Lett., 7 (1961) 118). Since then, the interest in this field has grown and various nonlinear optical effects are utilized for purposes such as nonlinear microscopy, switching, harmonic generation, parametric downconversion, filamentation, etc. We present here a brief overview of the various aspects on nonlinear optics and some of the recent advances in the field. c Societ`a Italiana di Fisica 31 32 S. Choudhary and R. W. Boyd 1. – Introduction to nonlinear optics Accordingˇ¡proofsAuthor please note that we have written in full the reference quota- tions in the abstract and reordered those in the text accordingly, following the numerical sequence.
    [Show full text]
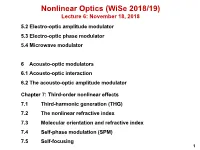
  • Nonlinear Optics (Wise 2018/19) Lecture 6: November 18, 2018 5.2 Electro-Optic Amplitude Modulator 5.3 Electro-Optic Phase Modulator 5.4 Microwave Modulator
    Nonlinear Optics (WiSe 2018/19) Lecture 6: November 18, 2018 5.2 Electro-optic amplitude modulator 5.3 Electro-optic phase modulator 5.4 Microwave modulator 6 Acousto-optic modulators 6.1 Acousto-optic interaction 6.2 The acousto-optic amplitude modulator Chapter 7: Third-order nonlinear effects 7.1 Third-harmonic generation (THG) 7.2 The nonlinear refractive index 7.3 Molecular orientation and refractive index 7.4 Self-phase modulation (SPM) 7.5 Self-focusing 1 5.2 Electro-optic amplitude modulator How is phase retardation converted into a amplitude modulation? 5.2. ELECTRO-OPTIC AMPLITUDE MODULATOR 93 0 direction input polarizer wave plate output polarizer Figure 5.7: Transversal electro-optic amplitude modulator from LiNbO3. Here, ∆φWP is the phase retardation due to the field-independent birefrin- 2 gence or due to an additional wave plate as shown in Fig. 5.7, and a is a co- efficient describing the relationship between field-dependent phase retardation and applied voltage. Usually we use β =45◦ to achieve 100 % transmission Iout 1 = 1 cos [∆φWP + aV (t)] (5.43) Iin 2 { − } 1 = 1 cos ∆φ cos [aV (t)] + sin ∆φ sin [aV (t)] . 2 { − WP WP } There are various applications for modulators. If the transmission through the modulator should be linearly dependent on the applied voltage, we use a bias ∆φ = π/2andobtainforaV 1 (see also Fig. 5.8) WP ≪ I 1 out = [1 + aV (t)] . (5.44) Iin 2 For a sinusoidal voltage V (t)=V0 sin ωmt (5.45) and constant input intensity, we obtain a sinusoidally varying output intensity Iout 1 = (1 + aV0 sin ωmt) .
    [Show full text]
  • The Mathematics of Nonlinear Optics
    The Mathematics of Nonlinear Optics Guy Metivier´ ∗ March 7, 2009 Contents 1 Introduction 4 2 Examples of equations arising in nonlinear optics 11 3 The framework of hyperbolic systems 18 3.1 Equations . 18 3.2 The dispersion relation & polarization conditions . 20 3.3 Existence and stability . 23 3.4 Continuation of solutions . 26 3.5 Global existence . 27 3.6 Local results . 29 4 Equations with parameters 32 4.1 Singular equations . 32 4.1.1 The weakly non linear case . 33 4.1.2 The case of prepared data . 34 4.1.3 Remarks on the commutation method . 38 4.1.4 Application 1 . 40 4.1.5 Application 2 . 41 4.2 Equations with rapidly varying coefficients . 45 ∗Universit´eBordeaux 1, IMB UMR 5251, 351 Cours de la Lib´eration,33405 Talence cedex, [email protected] 1 5 Geometrical Optics 49 5.1 Linear geometric optics . 49 5.1.1 An example using Fourier synthesis . 49 5.1.2 The BKW method and formal solutions . 51 5.1.3 The dispersion relation and phases . 52 5.1.4 The propagator of amplitudes . 53 5.1.5 Construction of WKB solutions . 60 5.1.6 Approximate solutions . 62 5.1.7 Exact solutions . 63 5.2 Weakly nonlinear geometric optics . 64 5.2.1 Asymptotic equations . 65 5.2.2 The structure of the profile equations I: the dispersive case . 67 5.2.3 The structure of the profile equation II : the nondispersive case; the generic Burger's eqation . 70 5.2.4 Approximate and exact solutions .
    [Show full text]
  • Nonlinear Optics: the Next Decade
    brought to you by View metadata, citation and similar papers at core.ac.uk CORE provided by The Australian National University Nonlinear optics: The next decade Yuri S. Kivshar Center for Ultra-high bandwidth Devices for Optical Systems (CUDOS), Nonlinear Physics Center, Research School of Physical Sciences and Engineering, Australian National University, Canberra ACT 0200, Australia Abstract: This paper concludes the Focus Serial assembled of invited papers in key areas of nonlinear optics (Editors: J.M. Dudley and R.W. Boyd), and it discusses new directions for future research in this field. © 2008 Optical Society of America OCIS codes: 190.0190 Nonlinear optics References and links 1. J.M. Dudley and R.W. Boyd, “Focus Series: Frontier of Nonlinear Optics. Introduction,” Optics Express 15, 5237-5237 (2007); http://www.opticsinfobase.org/oe/abstract.cfm?URI=oe-15-8-5237 Nonlinear optics describes the behavior of light in media with nonlinear response. Its tradi- tional topics cover different types of parametric processes, such as second-harmonic generation, as well as a variety of self-action effects, such as filamentation and solitons, typically observed at high light intensities delivered by pulsed lasers. While the study of nonlinear effects has a very long history going back to the physics of mechanical systems, the field of nonlinear op- tics is relatively young and, as a matter of fact, was born only after the invention of the laser. Soon after, the study of light-matter interaction emerged as an active direction of research and boosted the developments in material science and source technologies. Nowadays, nonlinear optics has evolved into many different branches, depending on the form of the material used for studying the nonlinear phenomena.
    [Show full text]
  • Rogue-Wave Solutions for an Inhomogeneous Nonlinear System in a Geophysical fluid Or Inhomogeneous Optical Medium
    Commun Nonlinear Sci Numer Simulat 36 (2016) 266–272 Contents lists available at ScienceDirect Commun Nonlinear Sci Numer Simulat journal homepage: www.elsevier.com/locate/cnsns Rogue-wave solutions for an inhomogeneous nonlinear system in a geophysical fluid or inhomogeneous optical medium Xi-Yang Xie a, Bo Tian a,∗, Yan Jiang a, Wen-Rong Sun a, Ya Sun a, Yi-Tian Gao b a State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China b Ministry-of-Education Key Laboratory of Fluid Mechanics and National Laboratory for Computational Fluid Dynamics, Beijing University of Aeronautics and Astronautics, Beijing 100191, China article info abstract Article history: Under investigation in this paper is an inhomogeneous nonlinear system, which describes Received 23 September 2015 the marginally-unstable baroclinic wave packets in a geophysical fluid or ultra-short pulses Accepted 3 December 2015 in nonlinear optics with certain inhomogeneous medium existing. By virtue of a kind of the Availableonline12December2015 Darboux transformation, under the Painlevé integrable condition, the first- and second-order bright and dark rogue-wave solutions are derived. Properties of the first- and second-order Keywords: α β Inhomogeneous nonlinear system bright and dark rogue waves with (t), which measures the state of the basic flow, and (t), Baroclinic wave packets in geophysical fluids representing the interaction of the wave packet and mean flow, are graphically presented and Ultra-short pulses in nonlinear optics analyzed: α(t)andβ(t) have no influence on the wave packet, but affect the correction of the Rogue-wave solution basic flow.
    [Show full text]
  • Nonlinear Optics in Daily Life
    Nonlinear optics in daily life Elsa Garmire* Thayer School of Engineering, Dartmouth College, 14 Engineering Drive, Hanover, NH, 03755, USA *[email protected] Abstract: An overview is presented of the impact of NLO on today’s daily life. While NLO researchers have promised many applications, only a few have changed our lives so far. This paper categorizes applications of NLO into three areas: improving lasers, interaction with materials, and information technology. NLO provides: coherent light of different wavelengths; multi-photon absorption for plasma-materials interaction; advanced spectroscopy and materials analysis; and applications to communications and sensors. Applications in information processing and storage seem less mature. © 2013 Optical Society of America OCIS codes: (190.0190) Nonlinear optics; (060.0060) Fiber optics and optical communications; (120.0120) Instrumentation, measurement, and metrology; (140.0140) Lasers and laser optics; (180.0180) Microscopy; (300.0300) Spectroscopy. References and Links 1. E. Garmire, “Overview of nonlinear optics,” open source, found at http://www.intechopen.com/books/nonlinear- optics/overview-of-nonlinear-optics. 2. E. Garmire, “Resource letter NO-1: nonlinear optics,” Am. J. Phys. 79(3), 245–255 (2011). 3. http://en.wikipedia.org/wiki/Laser_pointer. 4. http://www.coherent.com/products/?921/Mira-Family. 5. C. G. Durfee, T. Storz, J. Garlick, S. Hill, J. A. Squier, M. Kirchner, G. Taft, K. Shea, H. Kapteyn, M. Murnane, and S. Backus, “Direct diode-pumped Kerr-lens mode-locked Ti:sapphire laser,” Opt. Express 20(13), 13677– 13683 (2012). 6. http://www.continuumlasers.com/products/tunable_horizon_OPO.asp. 7. http://www.newport.com/Inspire-Automated-Ultrafast-OPOs/847655/1033/info.aspx.
    [Show full text]
  • Light-Wave Mixing and Scattering with Quantum Gases
    23rd International Laser Physics Workshop (LPHYS’14) IOP Publishing Journal of Physics: Conference Series 594 (2015) 012011 doi:10.1088/1742-6596/594/1/012011 Light-wave mixing and scattering with quantum gases L. Deng and E.W. Hagley National Institute of Standards and Technology, Gaithersburg, Maryland 20899 USA C.J. Zhu School of Physical Science and Engineering, Tongji University, Shanghai 200092, China E-mail: [email protected] Abstract: We show that optical processes originating from elementary excitations with dominant collective atomic recoil motion in a quantum gas can profoundly change many nonlinear optical processes routinely observed in a normal gas. Not only multi-photon wave mixing processes all become stimulated Raman or hyper-Raman in nature but the usual forward wave-mixing process, which is the most efficient process in normal gases, is strongly reduced by the condensate structure factor. On the other hand, in the backward direction the Bogoliubov dispersion automatically compensates the optical- wave phase mismatch, resulting in efficient backward light field generation that usually is not supported in normal gases. 1. Introduction Since the invention of the laser in 1960, the field of nonlinear optics has exploded. In a typical nonlinear optical process, often referred to as coherent wave-mixing, several photons are absorbed simultaneously by an atomic or molecular medium, and a photon with a different frequency is produced. Under the right conditions, the generated radiation may be coherently amplified by the quantum mechanical mechanism of stimulated emission identified by Albert Einstein. Today, 95 years after Einstein’s prediction, we are surrounded by practical applications of nonlinear optics, from multi-channel telecom lasers to the common laser pointer.
    [Show full text]
  • Learning Dominant Physical Processes with Data-Driven Balance Models ✉ Jared L
    ARTICLE https://doi.org/10.1038/s41467-021-21331-z OPEN Learning dominant physical processes with data-driven balance models ✉ Jared L. Callaham 1 , James V. Koch2, Bingni W. Brunton 3, J. Nathan Kutz4 & Steven L. Brunton1 Throughout the history of science, physics-based modeling has relied on judiciously approximating observed dynamics as a balance between a few dominant processes. How- ever, this traditional approach is mathematically cumbersome and only applies in asymptotic 1234567890():,; regimes where there is a strict separation of scales in the physics. Here, we automate and generalize this approach to non-asymptotic regimes by introducing the idea of an equation space, in which different local balances appear as distinct subspace clusters. Unsupervised learning can then automatically identify regions where groups of terms may be neglected. We show that our data-driven balance models successfully delineate dominant balance physics in a much richer class of systems. In particular, this approach uncovers key mechanistic models in turbulence, combustion, nonlinear optics, geophysical fluids, and neuroscience. 1 Department of Mechanical Engineering, University of Washington, Seattle, WA, USA. 2 Oden Institute for Computational & Engineering Sciences, University of Texas, Austin, TX, USA. 3 Department of Biology, University of Washington, Seattle, WA, USA. 4 Department of Applied Mathematics, University of ✉ Washington, Seattle, WA, USA. email: [email protected] NATURE COMMUNICATIONS | (2021) 12:1016 | https://doi.org/10.1038/s41467-021-21331-z | www.nature.com/naturecommunications 1 ARTICLE NATURE COMMUNICATIONS | https://doi.org/10.1038/s41467-021-21331-z t is well known across the engineering and physical sciences such models is not always necessary to describe the local behavior Ithat persistent behaviors in complex systems are often deter- of a system.
    [Show full text]
  • Nonlinear Optics and Nanophotonics November 25 - Decem Ber 6, 2013 Instituto De Física Teórica - UNESP - São Paulo, Brazil
    ICTP International Centre for Theoretical Physics SAIFR South American Institute for Fundamental Research São Paulo International Schools on Theoretical Physics Nonlinear Optics and Nanophotonics November 25 - Decem ber 6, 2013 Instituto de Física Teórica - UNESP - São Paulo, Brazil This school on Nonlinear Optics and Nanophotonics will cover the physics of nonlinear optical systems including photonic crystals and photonic lattices; Nonlinear optics at the nanoscale; Active optical media and laser dynamics; Nonlinear effects in optical communication systems; Metamaterials; Complex dynamics of quantum optical systems. ICTP-SAIFR Steering Committee: The school will end with a one day Workshop and precede the 6th Rio de la Plata Fernando Quevedo (chair) Workshop on Laser Dynamics and Nonlinear Photonics, which will be held in Montevideo, ICTP director Uruguay from December 9-12, 2013 (http://www.fisica.edu.uy/~cris/workshop.htm). Julio Cezar Durigan UNESP rector Carlos Brito Cruz Lecturers: FAPESP scientific director Thorsten Ackemann: Laser solitons, VCSEL, patterns and dynamics Jacob Palis University of Strathclyde, Scotland, UK Brasil Acad. of Sci. president Juan Maldacena Cid de Araujo: Nonlinear optical processes in condensed matter Representing South America Universidade Federal de Pernambuco, Brazil ICTP-SAIFR Marcel Clerc: Spatiotemporal chaotic localized states in optics Scientific Council: Universidad de Chile Peter Goddard (chair) Alexander Gaeta: Nonlinear interactions in optical waveguides IAS, Princeton Cornell University, USA S. Randjbar-Daemi (coord.) ICTP vice-director Dan Gauthier: Tailoring the group velocity and group velocity dispersion Juan Montero Duke University, USA IFT-UNESP director Marcela Carena Michal Lipson: Nanophotonic structures for extreme nonlinearities on-chip Fermilab, Batavia Cornell University, USA Marcel Clerc Univ.
    [Show full text]
  • Nonlinear Optics
    Nonlinear Optics Instructor: Mark G. Kuzyk Students: Benjamin R. Anderson Nathan J. Dawson Sheng-Ting Hung Wei Lu Shiva Ramini Jennifer L. Schei Shoresh Shafei Julian H. Smith Afsoon Soudi Szymon Steplewski Xianjun Ye August 4, 2010 2 Dedication We dedicate this book to everyone who is trying to learn nonlinear optics. i ii Preface This book grew out of lecture notes from the graduate course in Nonlinear Optics taught in spring 2010 at Washington State University. In its present form, this book is a first cut that is still in need of editing. The homework assignments and solutions are incomplete and will be added at a later time. Mark G. Kuzyk July, 2010 Pullman, WA iii iv Contents Dedication i Preface iii 1 Introduction to Nonlinear Optics 1 1.1 History . 1 1.1.1 Kerr Effect . 1 1.1.2 Two-Photon Absorption . 3 1.1.3 Second Harmonic Generation . 4 1.1.4 Optical Kerr Effect . 5 1.2 Units . 7 1.3 Example: Second Order Susceptibility . 8 1.4 Maxwell's Equations . 10 1.4.1 Electric displacement . 11 1.4.2 The Polarization . 13 1.5 Interaction of Light with Matter . 14 1.6 Goals . 19 2 Models of the NLO Response 21 2.1 Harmonic Oscillator . 21 2.1.1 Linear Harmonic Oscillator . 21 2.1.2 Nonlinear Harmonic Oscillator . 23 2.1.3 Non-Static Harmonic Oscillator . 26 2.2 Macroscopic Propagation . 30 2.3 Response Functions . 38 2.3.1 Time Invariance . 39 2.3.2 Fourier Transforms of Response Functions: Electric Susceptibilities .
    [Show full text]
  • L1 Logistics. Intro To
    OSE 6334 Nonlinear Optics Konstantin Vodopyanov 1 1 Lecture 1 Introduction to nonlinear optics. Logistics. 2 2 1 What this course is about This course gives a broad introduction to the field of Nonlinear Optics (NLO). The goal is to get you acquainted with the main effects of nonlinear optics and also introduce main equations that govern nonlinear-optical interactions. Beginning with a simple electron on a spring model—the course gives comprehensive explanations of second-order and third-order nonlinear effects and their physical origins. The corse covers nonlinear optics from a combined: physics, optics, materials science, and devices perspective. Examples will be given on solving practical problems such as design of nonlinear frequency converters, and also devices using ultrafast and high intensity lasers. 3 3 Newton’s superposition principle f(A+B) = f(A) + f(B) B Isaac Newton 1642 –1726 A Newton: Light cannot interact with light. Two beams of light can have no effect on each other. 4 4 2 Nonlinear optics f(A+B) ≠ f(A) + f(B) Beams A and B can create beam C Nicolaas Bloembergen B 1920–2017 Nobel Prize in Physics (1981) C A NLO: photons do interact 5 5 Linear Optics • The optical properties such as the refractive index and the absorption coefficient are independent of light intensity. • The Newton’s principle of superposition: light cannot interact with light. Two beams of light in the same region of a linear optical medium can have no effect on each other. Thus light cannot control light. • The frequency of light cannot be altered by its passage through the medium.
    [Show full text]
  • Entropic Thermodynamics of Nonlinear Photonic Chain Networks
    ARTICLE https://doi.org/10.1038/s42005-020-00484-1 OPEN Entropic thermodynamics of nonlinear photonic chain networks Fan O. Wu 1,4, Pawel S. Jung1,2,4, Midya Parto 1, Mercedeh Khajavikhan3 & ✉ Demetrios N. Christodoulides 1 1234567890():,; The convoluted nonlinear behaviors of heavily multimode photonic structures have been recently the focus of considerable attention. The sheer complexity associated with such multimode systems, allows them to display a host of phenomena that are otherwise impossible in few-mode settings. At the same time, however, it introduces a set of funda- mental challenges in terms of comprehending and harnessing their response. Here, we develop an optical thermodynamic approach capable of describing the thermalization dynamics in large scale nonlinear photonic tight-binding networks. For this specific system, an optical Sackur-Tetrode equation is obtained that explicitly provides the optical tempera- ture and chemical potential of the photon gas. Processes like isentropic expansion/com- pression, Joule expansion, as well as aspects associated with beam cleaning/cooling and thermal conduction effects in such chain networks are discussed. Our results can be used to describe in an effortless manner the exceedingly complex dynamics of highly multimoded nonlinear bosonic systems. 1 CREOL, College of Optics and Photonics, University of Central Florida, Orlando, FL 32816-2700, USA. 2 Faculty of Physics, Warsaw University of Technology, Koszykowa 75, 00-662 Warsaw, Poland. 3 Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, ✉ CA 9007, USA. 4These authors contributed equally: Fan O. Wu, Pawel S. Jung. email: [email protected] COMMUNICATIONS PHYSICS | (2020) 3:216 | https://doi.org/10.1038/s42005-020-00484-1 | www.nature.com/commsphys 1 ARTICLE COMMUNICATIONS PHYSICS | https://doi.org/10.1038/s42005-020-00484-1 n recent years, there has been considerable interest in available modes M, and the input optical power P.
    [Show full text]