DOCSLIB.ORG

An Introduction to Floating-Point Arithmetic and Computation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

An Introduction to Floating-Point Arithmetic and Computation Jeff Arnold CERN openlab 9 May 2017 c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 1 Agenda • Introduction • Standards • Properties • Error-Free Transformations • Summation Techniques • Dot Products • Polynomial Evaluation • Value Safety • Pitfalls and Gremlins • Tools • References and Bibliography c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 2 Why is Floating-Point Arithmetic Important? • It is ubiquitous in scientific computing • Most research in HEP can't be done without it • Algorithms are needed which • Get the best answers • Get the best answers all the time • \Best"means the right answer for the situation and context • There is always a compromise between fast and accurate c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 3 Important to Teach About Floating-Point Arithmetic • A rigorous approach to floating-point arithmetic is seldom taught in programming courses • Not enough physicists/programmers study numerical analysis • Many physicists/programmers think floating-point arithmetic is • inaccurate and ill-defined • filled with unpredictable behaviors and random errors • mysterious • Physicists/programmers need to be able to develop correct, accurate and robust algorithms • they need to be able to write good code to implement those algorithms c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 4 Reasoning about Floating-Point Arithmetic Reasoning about floating-point arithmetic is important because • One can prove algorithms are correct without exhaustive evaluation • One can determine when they fail • One can prove algorithms are portable • One can estimate the errors in calculations • Hardware changes have made floating-point calculations appear to be less deterministic • SIMD instructions • hardware threading Accurate knowledge about these factors increases confidence in floating-point computations c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 5 Classification of real numbers In mathematics, the set of real numbers R consists of • rational numbers Q fp=q : p; q 2 Z; q 6= 0g • integers Z fp : jpj 2 Wg • whole W fp : p 2 N [ 0g • natural N fp : p 2 f1; 2; :::gg • irrational numbers fx : x 2 R x2 = Qg • algebraic numbers A • transcendental numbers Dyadic rationals: ratio of an integer and 2b where b is a whole number c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 6 Some Properties of Floating-Point Numbers Floating-point numbers do not behave as do the real numbers encountered in mathematics. While all floating-point numbers are rational numbers • The set of floating-point numbers does not form a field under the usual set of arithmetic operations • Some common rules of arithmetic are not always valid when applied to floating-point operations • There are only a finite number of floating-point numbers c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 7 Floating-Point Numbers are Rational Numbers What does this imply? • Since there are only a finite number of floating-point numbers, there are rational numbers which are not floating-point numbers • The decimal equivalent of any finite floating-point value contains a finite number of non-zero digits p • The values of transcendentals such as π, e and 2 cannot be represented exactly by a floating-point value regardless of format or precision c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 8 How Many Floating-Point Numbers Are There? p+1 • ∼ 2 (2emax + 1) • Single-precision: ∼ 4:3 × 109 • Double-precision: ∼ 1:8 × 1019 • Number of protons circulating in LHC: ∼ 6:7 × 1014 c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 9 Standards There have been three major standards affecting floating-point arithmetic: • IEEE 754-1985 Standard for Binary Floating-Point Arithmetic • IEEE 854-1987 Standard for Radix-Independent Floating-Point Arithmetic • IEEE 754-2008 Standard for Floating-Point Arithmetic • This is the current standard • It is also an ISO standard (ISO/IEC/IEEE 60559:2011) c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 10 IEEE 754-2008 • Merged IEEE 754-1985 and IEEE 854-1987 • Tried not to invalidate hardware which conformed to IEEE 754-1985 • Standardized larger formats • For example, quad-precision format • Standardized new instructions • For example, fused multiply-add (FMA) From now on, we will only talk about IEEE 754-2008 c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 11 Operations Specified by IEEE 754-2008 All these operations must return the correct finite-precision result using the current rounding mode • Addition • Subtraction • Multiplication • Division • Remainder • Fused multiply add (FMA) • Square root • Comparison c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 12 Other Operations Specified by IEEE 754-2008 • Conversions between different floating-point formats • Conversions between floating-point and integer formats • Conversion to integer must be correctly rounded • Conversion between floating-point formats and external representations as character sequences • Conversions must be monotonic • Under some conditions, binary ! decimal ! binary conversions must be exact (\round-trip"conversions) c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 13 Special Values • Zero • zero is signed • Infinity • infinity is signed • Subnormals • NaN (Not a Number) • Quiet NaN • Signaling NaN • NaNs do not have a sign c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 14 Rounding Modes in IEEE 754-2008 The result must be the infinity-precise result rounded to the desired floating-point format. Possible rounding modes are • Round to nearest • round to nearest even • in the case of ties, select the result with a significand which is even • required for binary and decimal • the default rounding mode for binary • round to nearest away • required only for decimal • round toward 0 • round toward +1 • round toward −∞ c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 15 Exceptions Specified by IEEE 754-2008 • Underflow • Absolute value of a non-zero result is less than the smallest non-zero finite floating-point number • Result is 0 • Overflow • Absolute value of a result is greater than the largest finite floating-point number • Result is ±∞ • Division by Zero • x=y where x is finite and non-zero and y = 0 • Inexact • The result, after rounding, is different than the infinitely-precise result c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 16 Exceptions Specified by IEEE 754-2008 • Invalid • pAn operand is a NaN • x where x < 0 p • however, −0 = −0 • (±∞) ± (±∞) • (±0) × (±∞) • (±0)=(±0) • (±∞)=(±∞) • some floating-point!integer or decimal conversions c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 17 Formats Specified in IEEE 754-2008 Formats • Basic Formats: • Binary with sizes of 32, 64 and 128 bits • Decimal with sizes of 64 and 128 bits • Other formats: • Binary with a size of 16 bits • Decimal with a size of 32 bits c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 18 Transcendental and Algebraic Functions The standard recommends the following functions be correctly rounded: • ex; ex − 1; 2x; 2x − 1; 10x; 10x − 1 • logα(Φ) for α = e; 2; 10 and Φ = x; 1 + x p • px2 + y2; 1= x; (1 + x)n; xn; x1=n • sin(x); cos(x); tan(x); sinh(x); cosh(x); tanh(x) and their inverse functions • sin(πx); cos(πx) • And more ::: c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 19 We're Not Going to Consider Everything... The rest of this talk will be limited to the following aspects of IEEE 754-2008: • Binary32, Binary64 and Binary128 formats • The radix in these cases is always 2: β = 2 • This includes the formats handled by the SSE and AVX instruction sets on the x86 architecture • We will not consider any aspects of decimal arithmetic or the decimal formats • We will not consider \double extended"format • Also known as the \IA32 x87"format • The rounding mode is assumed to be round-to-nearest-even c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 20 Storage Format of a Binary Floating-Point Number p − 1 bits w bits - - s E significand IEEE Name Format Size w p emin emax Binary32 Single 32 8 24 -126 +127 Binary64 Double 64 11 53 -1022 +1023 Binary128 Quad 128 15 113 -16382 +16383 Notes: • E = e − emin + 1 • emax = −emin + 1 • p − 1 will be addressed later c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 21 The Value of a Floating-Point Number The format of a floating-point number is determined by the quantities: • radix β • sometimes called the \base" • sign s 2 f0; 1g • exponent e • an integer such that emin ≤ e ≤ emax • precision p • the number of \digits"in the number c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 22 The Value of a Floating-Point Number The value of a floating-point number is determined by • the format of the number • the digits in the number: xi, 0 ≤ i < p, where 0 ≤ xi < β. The value of a floating-point number can be expressed as p−1 s e X −i x = (−) β xiβ i=0 where the significand is p−1 X −i m = xiβ i=0 with 0 ≤ m < β c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 23 The Value of a Floating-Point Number The value of a floating-point number can also be written p−1 s e−p+1 X p−i−1 x = (−) β xiβ i=0 where the integral significand is p−1 X p−i−1 M = xiβ i=0 and M is an integer such that 0 ≤ M < βp c 2017 Jeffrey M. Arnold Floating-Point Arithmetic and Computation 24 The Value of a Floating-Point Number The value of a floating-point number can also be written as 8 M < (−)s if e − p + 1 < 0 x = β−(e−p+1) : (−)sβe−p+1M if e − p + 1 ≥ 0 where M is the integral significand.
Recommended publications
  • Division by Zero Calculus and Singular Integrals

    Division by Zero Calculus and Singular Integrals

    Proceedings of International Conference on Mechanical, Electrical and Medical Intelligent System 2017 Division by Zero Calculus and Singular Integrals Tsutomu Matsuura1, a and Saburou Saitoh2,b 1Faculty of Science and Technology, Gunma University, 1-5-1 Tenjin-cho, Kiryu 376-8515, Japan 2Institute of Reproducing Kernels, Kawauchi-cho, 5-1648-16, Kiryu 376-0041, Japan [email protected], [email protected] Keywords: division by zero, point at infinity, singularity, Laurent expansion, Hadamard finite part Abstract. In this paper, we will introduce the formulas log 0= log ∞= 0 (not as limiting values) in the meaning of the one point compactification of Aleksandrov and their fundamental applications, and we will also examine the relationship between Laurent expansion and the division by zero. Based on those examinations we give the interpretation for the Hadamard finite part of singular integrals by means of the division by zero calculus. In particular, we will know that the division by zero is our elementary and fundamental mathematics. 1. Introduction By a natural extension of the fractions b (1) a for any complex numbers a and b , we found the simple and beautiful result, for any complex number b b = 0, (2) 0 incidentally in [1] by the Tikhonov regularization for the Hadamard product inversions for matrices and we discussed their properties and gave several physical interpretations on the general fractions in [2] for the case of real numbers. The result is very special case for general fractional functions in [3]. The division by zero has a long and mysterious story over the world (see, for example, H.
  • The Role of the Interval Domain in Modern Exact Real Airthmetic

    The Role of the Interval Domain in Modern Exact Real Airthmetic

    The Role of the Interval Domain in Modern Exact Real Airthmetic Andrej Bauer Iztok Kavkler Faculty of Mathematics and Physics University of Ljubljana, Slovenia Domains VIII & Computability over Continuous Data Types Novosibirsk, September 2007 Teaching theoreticians a lesson Recently I have been told by an anonymous referee that “Theoreticians do not like to be taught lessons.” and by a friend that “You should stop competing with programmers.” In defiance of this advice, I shall talk about the lessons I learned, as a theoretician, in programming exact real arithmetic. The spectrum of real number computation slow fast Formally verified, Cauchy sequences iRRAM extracted from streams of signed digits RealLib proofs floating point Moebius transformtions continued fractions Mathematica "theoretical" "practical" I Common features: I Reals are represented by successive approximations. I Approximations may be computed to any desired accuracy. I State of the art, as far as speed is concerned: I iRRAM by Norbert Muller,¨ I RealLib by Branimir Lambov. What makes iRRAM and ReaLib fast? I Reals are represented by sequences of dyadic intervals (endpoints are rationals of the form m/2k). I The approximating sequences need not be nested chains of intervals. I No guarantee on speed of converge, but arbitrarily fast convergence is possible. I Previous approximations are not stored and not reused when the next approximation is computed. I Each next approximation roughly doubles the amount of work done. The theory behind iRRAM and RealLib I Theoretical models used to design iRRAM and RealLib: I Type Two Effectivity I a version of Real RAM machines I Type I representations I The authors explicitly reject domain theory as a suitable computational model.
  • Division by Fractions 6.1.1 - 6.1.4

    Division by Fractions 6.1.1 - 6.1.4

    DIVISION BY FRACTIONS 6.1.1 - 6.1.4 Division by fractions introduces three methods to help students understand how dividing by fractions works. In general, think of division for a problem like 8..,.. 2 as, "In 8, how many groups of 2 are there?" Similarly, ½ + ¼ means, "In ½ , how many fourths are there?" For more information, see the Math Notes boxes in Lessons 7.2 .2 and 7 .2 .4 of the Core Connections, Course 1 text. For additional examples and practice, see the Core Connections, Course 1 Checkpoint 8B materials. The first two examples show how to divide fractions using a diagram. Example 1 Use the rectangular model to divide: ½ + ¼ . Step 1: Using the rectangle, we first divide it into 2 equal pieces. Each piece represents ½. Shade ½ of it. - Step 2: Then divide the original rectangle into four equal pieces. Each section represents ¼ . In the shaded section, ½ , there are 2 fourths. 2 Step 3: Write the equation. Example 2 In ¾ , how many ½ s are there? In ¾ there is one full ½ 2 2 I shaded and half of another Thatis,¾+½=? one (that is half of one half). ]_ ..,_ .l 1 .l So. 4 . 2 = 2 Start with ¾ . 3 4 (one and one-half halves) Parent Guide with Extra Practice © 2011, 2013 CPM Educational Program. All rights reserved. 49 Problems Use the rectangular model to divide. .l ...:... J_ 1 ...:... .l 1. ..,_ l 1 . 1 3 . 6 2. 3. 4. 1 4 . 2 5. 2 3 . 9 Answers l. 8 2. 2 3. 4 one thirds rm I I halves - ~I sixths fourths fourths ~I 11 ~'.¿;¡~:;¿~ ffk] 8 sixths 2 three fourths 4.
  • United States Patent [19] [11] E Patent Number: Re

    United States Patent [19] [11] E Patent Number: Re

    United States Patent [19] [11] E Patent Number: Re. 33,629 Palmer et a1. [45] Reissued Date of Patent: Jul. 2, 1991 [54] NUMERIC DATA PROCESSOR 1973, IEEE Transactions on Computers vol. C-22, pp. [75] Inventors: John F. Palmer, Cambridge, Mass; 577-586. Bruce W. Ravenel, Nederland, Co1o.; Bulman, D. M. "Stack Computers: An Introduction," Ra? Nave, Haifa, Israel May 1977, Computer pp. 18-28. Siewiorek, Daniel H; Bell, C. Gordon; Newell, Allen, [73] Assignee: Intel Corporation, Santa Clara, Calif. “Computer Structures: Principles and Examples," 1977, [21] Appl. No.: 461,538 Chapter 29, pp. 470-485 McGraw-Hill Book Co. Palmer, John F., “The Intel Standard for Floatin [22] Filed: Jun. 1, 1990 g-Point Arithmetic,“ Nov. 8-11, 1977, IEEE COMP SAC 77 Proceedings, 107-112. Related US. Patent Documents Coonen, J. T., "Speci?cations for a Proposed Standard Reissue of: t for Floating-Point Arithmetic," Oct. 13, 1978, Mem. [64] Patent No.: 4,338,675 #USB/ERL M78172, pp. 1-32. Issued: Jul. 6, 1982 Pittman, T. and Stewart, R. G., “Microprocessor Stan Appl. No: 120.995 dards,” 1978, AFIPS Conference Proceedings, vol. 47, Filed: Feb. 13, 1980 pp. 935-938. “7094-11 System Support For Numerical Analysis,“ by [51] Int. Cl.-‘ ........................ .. G06F 7/48; G06F 9/00; William Kahan, Dept. of Computer Science, Univ. of G06F 11/00 Toronto, Aug. 1966, pp. 1-51. [52] US. Cl. .................................. .. 364/748; 364/737; “A Uni?ed Decimal Floating-Point Architecture For 364/745; 364/258 The Support of High-Level Languages,‘ by Frederic [58] Field of Search ............. .. 364/748, 745, 737, 736, N.
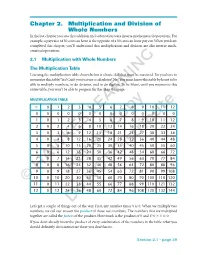
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations

    Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations

    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
  • Faster Math Functions, Soundly

    Faster Math Functions, Soundly

    Faster Math Functions, Soundly IAN BRIGGS, University of Utah, USA PAVEL PANCHEKHA, University of Utah, USA Standard library implementations of functions like sin and exp optimize for accuracy, not speed, because they are intended for general-purpose use. But applications tolerate inaccuracy from cancellation, rounding error, and singularities—sometimes even very high error—and many application could tolerate error in function implementations as well. This raises an intriguing possibility: speeding up numerical code by tuning standard function implementations. This paper thus introduces OpTuner, an automatic method for selecting the best implementation of mathematical functions at each use site. OpTuner assembles dozens of implementations for the standard mathematical functions from across the speed-accuracy spectrum. OpTuner then uses error Taylor series and integer linear programming to compute optimal assignments of function implementation to use site and presents the user with a speed-accuracy Pareto curve they can use to speed up their code. In a case study on the POV-Ray ray tracer, OpTuner speeds up a critical computation, leading to a whole program speedup of 9% with no change in the program output (whereas human efforts result in slower code and lower-quality output). On a broader study of 37 standard benchmarks, OpTuner matches 216 implementations to 89 use sites and demonstrates speed-ups of 107% for negligible decreases in accuracy and of up to 438% for error-tolerant applications. Additional Key Words and Phrases: Floating point, rounding error, performance, approximation theory, synthesis, optimization 1 INTRODUCTION Floating-point arithmetic is foundational for scientific, engineering, and mathematical software. This is because, while floating-point arithmetic is approximate, most applications tolerate minute errors [Piparo et al.
  • Division by Zero in Logic and Computing Jan Bergstra

    Division by Zero in Logic and Computing Jan Bergstra

    Division by Zero in Logic and Computing Jan Bergstra To cite this version: Jan Bergstra. Division by Zero in Logic and Computing. 2021. hal-03184956v2 HAL Id: hal-03184956 https://hal.archives-ouvertes.fr/hal-03184956v2 Preprint submitted on 19 Apr 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. DIVISION BY ZERO IN LOGIC AND COMPUTING JAN A. BERGSTRA Abstract. The phenomenon of division by zero is considered from the per- spectives of logic and informatics respectively. Division rather than multi- plicative inverse is taken as the point of departure. A classification of views on division by zero is proposed: principled, physics based principled, quasi- principled, curiosity driven, pragmatic, and ad hoc. A survey is provided of different perspectives on the value of 1=0 with for each view an assessment view from the perspectives of logic and computing. No attempt is made to survey the long and diverse history of the subject. 1. Introduction In the context of rational numbers the constants 0 and 1 and the operations of addition ( + ) and subtraction ( − ) as well as multiplication ( · ) and division ( = ) play a key role. When starting with a binary primitive for subtraction unary opposite is an abbreviation as follows: −x = 0 − x, and given a two-place division function unary inverse is an abbreviation as follows: x−1 = 1=x.
  • IEEE Standard 754 for Binary Floating-Point Arithmetic

    IEEE Standard 754 for Binary Floating-Point Arithmetic

    Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite
  • SPARC Assembly Language Reference Manual

    SPARC Assembly Language Reference Manual

    SPARC Assembly Language Reference Manual 2550 Garcia Avenue Mountain View, CA 94043 U.S.A. A Sun Microsystems, Inc. Business 1995 Sun Microsystems, Inc. 2550 Garcia Avenue, Mountain View, California 94043-1100 U.S.A. All rights reserved. This product or document is protected by copyright and distributed under licenses restricting its use, copying, distribution and decompilation. No part of this product or document may be reproduced in any form by any means without prior written authorization of Sun and its licensors, if any. Portions of this product may be derived from the UNIX® system, licensed from UNIX Systems Laboratories, Inc., a wholly owned subsidiary of Novell, Inc., and from the Berkeley 4.3 BSD system, licensed from the University of California. Third-party software, including font technology in this product, is protected by copyright and licensed from Sun’s Suppliers. RESTRICTED RIGHTS LEGEND: Use, duplication, or disclosure by the government is subject to restrictions as set forth in subparagraph (c)(1)(ii) of the Rights in Technical Data and Computer Software clause at DFARS 252.227-7013 and FAR 52.227-19. The product described in this manual may be protected by one or more U.S. patents, foreign patents, or pending applications. TRADEMARKS Sun, Sun Microsystems, the Sun logo, SunSoft, the SunSoft logo, Solaris, SunOS, OpenWindows, DeskSet, ONC, ONC+, and NFS are trademarks or registered trademarks of Sun Microsystems, Inc. in the United States and other countries. UNIX is a registered trademark in the United States and other countries, exclusively licensed through X/Open Company, Ltd. OPEN LOOK is a registered trademark of Novell, Inc.
  • X86-64 Machine-Level Programming∗

    X86-64 Machine-Level Programming∗

    x86-64 Machine-Level Programming∗ Randal E. Bryant David R. O'Hallaron September 9, 2005 Intel’s IA32 instruction set architecture (ISA), colloquially known as “x86”, is the dominant instruction format for the world’s computers. IA32 is the platform of choice for most Windows and Linux machines. The ISA we use today was defined in 1985 with the introduction of the i386 microprocessor, extending the 16-bit instruction set defined by the original 8086 to 32 bits. Even though subsequent processor generations have introduced new instruction types and formats, many compilers, including GCC, have avoided using these features in the interest of maintaining backward compatibility. A shift is underway to a 64-bit version of the Intel instruction set. Originally developed by Advanced Micro Devices (AMD) and named x86-64, it is now supported by high end processors from AMD (who now call it AMD64) and by Intel, who refer to it as EM64T. Most people still refer to it as “x86-64,” and we follow this convention. Newer versions of Linux and GCC support this extension. In making this switch, the developers of GCC saw an opportunity to also make use of some of the instruction-set features that had been added in more recent generations of IA32 processors. This combination of new hardware and revised compiler makes x86-64 code substantially different in form and in performance than IA32 code. In creating the 64-bit extension, the AMD engineers also adopted some of the features found in reduced-instruction set computers (RISC) [7] that made them the favored targets for optimizing compilers.
  • Classical Logic and the Division by Zero Ilija Barukčić#1 #Internist Horandstrasse, DE-26441 Jever, Germany

    Classical Logic and the Division by Zero Ilija Barukčić#1 #Internist Horandstrasse, DE-26441 Jever, Germany

    International Journal of Mathematics Trends and Technology (IJMTT) – Volume 65 Issue 8 – August 2019 Classical logic and the division by zero Ilija Barukčić#1 #Internist Horandstrasse, DE-26441 Jever, Germany Abstract — The division by zero turned out to be a long lasting and not ending puzzle in mathematics and physics. An end of this long discussion appears not to be in sight. In particular zero divided by zero is treated as indeterminate thus that a result cannot be found out. It is the purpose of this publication to solve the problem of the division of zero by zero while relying on the general validity of classical logic. A systematic re-analysis of classical logic and the division of zero by zero has been undertaken. The theorems of this publication are grounded on classical logic and Boolean algebra. There is some evidence that the problem of zero divided by zero can be solved by today’s mathematical tools. According to classical logic, zero divided by zero is equal to one. Keywords — Indeterminate forms, Classical logic, Zero divided by zero, Infinity I. INTRODUCTION Aristotle‘s unparalleled influence on the development of scientific knowledge in western world is documented especially by his contributions to classical logic too. Besides of some serious limitations of Aristotle‘s logic, Aristotle‘s logic became dominant and is still an adequate basis of our understanding of science to some extent, since centuries. In point of fact, some authors are of the opinion that Aristotle himself has discovered everything there was to know about classical logic. After all, classical logic as such is at least closely related to the study of objective reality and deals with absolutely certain inferences and truths.
  • Complete Interval Arithmetic and Its Implementation on the Computer

    Complete Interval Arithmetic and Its Implementation on the Computer

    Complete Interval Arithmetic and its Implementation on the Computer Ulrich W. Kulisch Institut f¨ur Angewandte und Numerische Mathematik Universit¨at Karlsruhe Abstract: Let IIR be the set of closed and bounded intervals of real numbers. Arithmetic in IIR can be defined via the power set IPIR (the set of all subsets) of real numbers. If divisors containing zero are excluded, arithmetic in IIR is an algebraically closed subset of the arithmetic in IPIR, i.e., an operation in IIR performed in IPIR gives a result that is in IIR. Arithmetic in IPIR also allows division by an interval that contains zero. Such division results in closed intervals of real numbers which, however, are no longer bounded. The union of the set IIR with these new intervals is denoted by (IIR). The paper shows that arithmetic operations can be extended to all elements of the set (IIR). On the computer, arithmetic in (IIR) is approximated by arithmetic in the subset (IF ) of closed intervals over the floating-point numbers F ⊂ IR. The usual exceptions of floating-point arithmetic like underflow, overflow, division by zero, or invalid operation do not occur in (IF ). Keywords: computer arithmetic, floating-point arithmetic, interval arithmetic, arith- metic standards. 1 Introduction or a Vision of Future Computing Computers are getting ever faster. The time can already be foreseen when the P C will be a teraflops computer. With this tremendous computing power scientific computing will experience a significant shift from floating-point arithmetic toward increased use of interval arithmetic. With very little extra hardware, interval arith- metic can be made as fast as simple floating-point arithmetic [3].