The Role of the Interval Domain in Modern Exact Real Airthmetic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Algebraic Properties of the Richard Thompson's Group F
ALGEBRAIC PROPERTIES OF THE RICHARD THOMPSON’S GROUP F AND ITS APPLICATIONS IN CRYPTOGRAPHY A THESIS SUBMITTED TO THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCES OF MIDDLE EAST TECHNICAL UNIVERSITY BY HAKAN YETER IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS FEBRUARY 2021 Approval of the thesis: ALGEBRAIC PROPERTIES OF THE RICHARD THOMPSON’S GROUP F AND ITS APPLICATIONS IN CRYPTOGRAPHY submitted by HAKAN YETER in partial fulfillment of the requirements for the de- gree of Master of Science in Mathematics Department, Middle East Technical University by, Prof. Dr. Halil Kalıpçılar Dean, Graduate School of Natural and Applied Sciences Prof. Dr. Yıldıray Ozan Head of Department, Mathematics Assoc. Prof. Dr. Mustafa Gökhan Benli Supervisor, Mathematics Department, METU Examining Committee Members: Assoc. Prof. Dr. Fatih Sulak Mathematics Department, Atilim University Assoc. Prof. Dr. Mustafa Gökhan Benli Mathematics Department, METU Assist. Prof. Dr. Burak Kaya Mathematics Department, METU Date: I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work. Name, Surname: Hakan Yeter Signature : iv ABSTRACT ALGEBRAIC PROPERTIES OF THE RICHARD THOMPSON’S GROUP F AND ITS APPLICATIONS IN CRYPTOGRAPHY Yeter, Hakan M.S., Department of Mathematics Supervisor: Assoc. Prof. Dr. Mustafa Gökhan Benli February 2021, 69 pages Thompson’s groups F; T and V , especially F , are widely studied groups in group theory. -

Division by Fractions 6.1.1 - 6.1.4
DIVISION BY FRACTIONS 6.1.1 - 6.1.4 Division by fractions introduces three methods to help students understand how dividing by fractions works. In general, think of division for a problem like 8..,.. 2 as, "In 8, how many groups of 2 are there?" Similarly, ½ + ¼ means, "In ½ , how many fourths are there?" For more information, see the Math Notes boxes in Lessons 7.2 .2 and 7 .2 .4 of the Core Connections, Course 1 text. For additional examples and practice, see the Core Connections, Course 1 Checkpoint 8B materials. The first two examples show how to divide fractions using a diagram. Example 1 Use the rectangular model to divide: ½ + ¼ . Step 1: Using the rectangle, we first divide it into 2 equal pieces. Each piece represents ½. Shade ½ of it. - Step 2: Then divide the original rectangle into four equal pieces. Each section represents ¼ . In the shaded section, ½ , there are 2 fourths. 2 Step 3: Write the equation. Example 2 In ¾ , how many ½ s are there? In ¾ there is one full ½ 2 2 I shaded and half of another Thatis,¾+½=? one (that is half of one half). ]_ ..,_ .l 1 .l So. 4 . 2 = 2 Start with ¾ . 3 4 (one and one-half halves) Parent Guide with Extra Practice © 2011, 2013 CPM Educational Program. All rights reserved. 49 Problems Use the rectangular model to divide. .l ...:... J_ 1 ...:... .l 1. ..,_ l 1 . 1 3 . 6 2. 3. 4. 1 4 . 2 5. 2 3 . 9 Answers l. 8 2. 2 3. 4 one thirds rm I I halves - ~I sixths fourths fourths ~I 11 ~'.¿;¡~:;¿~ ffk] 8 sixths 2 three fourths 4. -
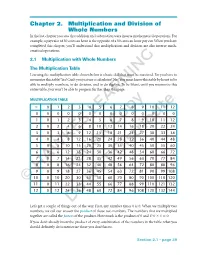
Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers. -

Dyadic Rationals and Surreal Number Theory C
IOSR Journal of Mathematics (IOSR-JM) e-ISSN: 2278-5728, p-ISSN: 2319-765X. Volume 16, Issue 5 Ser. IV (Sep. – Oct. 2020), PP 35-43 www.iosrjournals.org Dyadic Rationals and Surreal Number Theory C. Avalos-Ramos C.U.C.E.I. Universidad de Guadalajara, Guadalajara, Jalisco, México J. A. Félix-Algandar Facultad de Ciencias Físico-Matemáticas de la Universidad Autónoma de Sinaloa, 80010, Culiacán, Sinaloa, México. J. A. Nieto Facultad de Ciencias Físico-Matemáticas de la Universidad Autónoma de Sinaloa, 80010, Culiacán, Sinaloa, México. Abstract We establish a number of properties of the dyadic rational numbers associated with surreal number theory. In particular, we show that a two parameter function of dyadic rationals can give all the trees of n-days in surreal number formalism. --------------------------------------------------------------------------------------------------------------------------------------- Date of Submission: 07-10-2020 Date of Acceptance: 22-10-2020 --------------------------------------------------------------------------------------------------------------------------------------- I. Introduction In mathematics, from number theory history [1], one learns that historically, roughly speaking, the starting point was the natural numbers N and after a centuries of though evolution one ends up with the real numbers from which one constructs the differential and integral calculus. Surprisingly in 1973 Conway [2] (see also Ref. [3]) developed the surreal numbers structure which contains no only the real numbers , but also the hypereals and other numerical structures. Consider the set (1) and call and the left and right sets of , respectively. Surreal numbers are defined in terms of two axioms: Axiom 1. Every surreal number corresponds to two sets and of previously created numbers, such that no member of the left set is greater or equal to any member of the right set . -

Fast Integer Division – a Differentiated Offering from C2000 Product Family
Application Report SPRACN6–July 2019 Fast Integer Division – A Differentiated Offering From C2000™ Product Family Prasanth Viswanathan Pillai, Himanshu Chaudhary, Aravindhan Karuppiah, Alex Tessarolo ABSTRACT This application report provides an overview of the different division and modulo (remainder) functions and its associated properties. Later, the document describes how the different division functions can be implemented using the C28x ISA and intrinsics supported by the compiler. Contents 1 Introduction ................................................................................................................... 2 2 Different Division Functions ................................................................................................ 2 3 Intrinsic Support Through TI C2000 Compiler ........................................................................... 4 4 Cycle Count................................................................................................................... 6 5 Summary...................................................................................................................... 6 6 References ................................................................................................................... 6 List of Figures 1 Truncated Division Function................................................................................................ 2 2 Floored Division Function................................................................................................... 3 3 Euclidean -

Multiplication and Divisions
Third Grade Math nd 2 Grading Period Power Objectives: Academic Vocabulary: multiplication array Represent and solve problems involving multiplication and divisor commutative division. (P.O. #1) property Understand properties of multiplication and the distributive property relationship between multiplication and divisions. estimation division factor column (P.O. #2) Multiply and divide with 100. (P.O. #3) repeated addition multiple Solve problems involving the four operations, and identify associative property quotient and explain the patterns in arithmetic. (P.O. #4) rounding row product equation Multiplication and Division Enduring Understandings: Essential Questions: Mathematical operations are used in solving problems In what ways can operations affect numbers? in which a new value is produced from one or more How can different strategies be helpful when solving a values. problem? Algebraic thinking involves choosing, combining, and How does knowing and using algorithms help us to be applying effective strategies for answering questions. Numbers enable us to use the four operations to efficient problem solvers? combine and separate quantities. How are multiplication and addition alike? See below for additional enduring understandings. How are subtraction and division related? See below for additional essential questions. Enduring Understandings: Multiplication is repeated addition, related to division, and can be used to solve story problems. For a given set of numbers, there are relationships that -

AUTHOR Multiplication and Division. Mathematics-Methods
DOCUMENT RESUME ED 221 338 SE 035 008, AUTHOR ,LeBlanc, John F.; And Others TITLE Multiplication and Division. Mathematics-Methods 12rogram Unipt. INSTITUTION Indiana ,Univ., Bloomington. Mathematics Education !Development Center. , SPONS AGENCY ,National Science Foundation, Washington, D.C. REPORT NO :ISBN-0-201-14610-x PUB DATE 76 . GRANT. NSF-GY-9293 i 153p.; For related documents, see SE 035 006-018. NOTE . ,. EDRS PRICE 'MF01 Plus Postage. PC Not Available from EDRS. DESCRIPTORS iAlgorithms; College Mathematics; *Division; Elementary Education; *Elementary School Mathematics; 'Elementary School Teachers; Higher Education; 'Instructional1 Materials; Learning Activities; :*Mathematics Instruction; *Multiplication; *Preservice Teacher Education; Problem Solving; :Supplementary Reading Materials; Textbooks; ;Undergraduate Study; Workbooks IDENTIFIERS i*Mathematics Methods Program ABSTRACT This unit is 1 of 12 developed for the university classroom portign_of the Mathematics-Methods Program(MMP), created by the Indiana pniversity Mathematics EducationDevelopment Center (MEDC) as an innovative program for the mathematics training of prospective elenientary school teachers (PSTs). Each unit iswritten in an activity format that involves the PST in doing mathematicswith an eye towardaiplication of that mathematics in the elementary school. This do ument is one of four units that are devoted tothe basic number wo k in the elementary school. In addition to an introduction to the unit, the text has sections on the conceptual development of nultiplication -

Dyadic Polygons∗
May 18, 2011 15:21 WSPC/S0218-1967 132-IJAC S0218196711006248 International Journal of Algebra and Computation Vol. 21, No. 3 (2011) 387–408 c World Scientific Publishing Company DOI: 10.1142/S0218196711006248 DYADIC POLYGONS∗ K. MATCZAK Faculty of Civil Engineering, Mechanics and Petrochemistry in Plock Warsaw University of Technology 09-400 Plock, Poland [email protected] A. B. ROMANOWSKA Faculty of Mathematics and Information Science Warsaw University of Technology 00-661 Warsaw, Poland [email protected] J. D. H. SMITH Department of Mathematics Iowa State University, Ames, Iowa, 50011, USA [email protected] Received 20 November 2009 Revised 26 August 2010 Communicated by R. McKenzie Dyadic rationals are rationals whose denominator is a power of 2. Dyadic triangles and dyadic polygons are, respectively, defined as the intersections with the dyadic plane of a triangle or polygon in the real plane whose vertices lie in the dyadic plane. The one-dimensional analogs are dyadic intervals. Algebraically, dyadic polygons carry the structure of a commutative, entropic and idempotent algebra under the binary operation of arithmetic mean. In this paper, dyadic intervals and triangles are classified to within affine or algebraic isomorphism, and dyadic polygons are shown to be finitely generated as algebras. The auxiliary results include a form of Pythagoras’ theorem for dyadic affine geometry. Keywords: Affine space; convex set; polygon; polytope; commutative; binary; entropic mode; arithmetic mean. Mathematics Subject Classification: 20N02, 52C05 ∗Research was supported by the Warsaw University of Technology under grant number 504G/1120/0054/000. Part of the work on this paper was completed during several visits of the second author to Iowa State University, Ames, Iowa. -

On the Walsh Functions(*)
ON THE WALSH FUNCTIONS(*) BY N. J. FINE Table of Contents 1. Introduction. 372 2. The dyadic group. 376 3. Expansions of certain functions. 380 4. Fourier coefficients. 382 5. Lebesgue constants. 385 6. Convergence. 391 7. Summability. 395 8. On certain sums. 399 9. Uniqueness and localization. 402 1. Introduction. The system of orthogonal functions introduced by Rade- macher [6](2) has been the subject of a great deal of study. This system is not a complete one. Its completion was effected by Walsh [7], who studied some of its Fourier properties, such as convergence, summability, and so on. Others, notably Kaczmarz [3], Steinhaus [4], Paley [S], have studied various aspects of the Walsh system. Walsh has pointed out the great similarity be- tween this system and the trigonometric system. It is convenient, in defining the functions of the Walsh system, to follow Paley's modification. The Rademacher functions are defined by *»(*) = 1 (0 g x < 1/2), *»{«) = - 1 (1/2 á * < 1), <¡>o(%+ 1) = *o(«), *»(*) = 0o(2"x) (w = 1, 2, • • ■ ). The Walsh functions are then given by (1-2) to(x) = 1, Tpn(x) = <t>ni(x)<t>ni(x) ■ ■ ■ 4>nr(x) for » = 2"1 + 2n2+ • • • +2"r, where the integers »¿ are uniquely determined by «i+i<«¿. Walsh proves that {^„(x)} form a complete orthonormal set. Every periodic function f(x) which is integrable in the sense of Lebesgue on (0, 1) will have associated with it a (Walsh-) Fourier series (1.3) /(*) ~ Co+ ciipi(x) + crf/iix) + • • • , where the coefficients are given by Presented to the Society, August 23, 1946; received by the editors February 13, 1948. -

Understanding the Concept of Division
Understanding the Concept of Division ________________ An Honors thesis presented to the faculty of the Department of Mathematics East Tennessee State University In partial fulfillment of the requirements for the Honors-in-Discipline Program for a Bachelor of Science in Mathematics ________________ By Leanna Horton May, 2007 ________________ George Poole, Ph.D. Advisor approval: ___________________________ ABSTRACT Understanding the Concept of Division by Leanna Horton The purpose of this study was to assess how well elementary students and mathematics educators understand the concept of division. Participants included 210 fourth and fifth grade students, 17 elementary math teachers, and seven collegiate level math faculty. The problems were designed to assess whether or not participants understood when a solution would include a remainder and if they could accurately explain their responses, including giving appropriate units to all numbers in their solution. The responses given by all participants and the methods used by the elementary students were analyzed. The results indicate that a significant number of the student participants had difficulties giving complete, accurate explanations to some of the problems. The results also indicate that both the elementary students and teachers had difficulties understanding when a solution will include a remainder and when it will include a fraction. The analysis of the methods used indicated that the use of long division or pictures produced the most accurate solutions. 2 CONTENTS Page ABSTRACT………………………………………………………………………… 2 LIST OF TABLES………………………………………………………………….. 6 LIST OF FIGURES………………………………………………………………… 7 1 Introduction…………………………………………………………………. 8 Purpose……………………………………………………………… 8 Literature Review…………………………………………………… 9 Teachers..…………………………………………………….. 9 Students…………………………………………………….. 10 Math and Gender……………………………………………. 13 Word Problems……………………………………………………… 14 Number of Variables……………………………………….. 15 Types of Variables…………………………………………. -

Interpreting Multiplication and Division
CONCEPT DEVELOPMENT Mathematics Assessment Project CLASSROOM CHALLENGES A Formative Assessment Lesson Interpreting Multiplication and Division Mathematics Assessment Resource Service University of Nottingham & UC Berkeley For more details, visit: http://map.mathshell.org © 2015 MARS, Shell Center, University of Nottingham May be reproduced, unmodified, for non-commercial purposes under the Creative Commons license detailed at http://creativecommons.org/licenses/by-nc-nd/3.0/ - all other rights reserved Interpreting Multiplication and Division MATHEMATICAL GOALS This lesson unit is designed to help students to interpret the meaning of multiplication and division. Many students have a very limited understanding of these operations and only recognise them in terms of ‘times’ and ‘share’. They find it hard to give any meaning to calculations that involve non- integers. This is one reason why they have difficulty when choosing the correct operation to perform when solving word problems. COMMON CORE STATE STANDARDS This lesson relates to the following Standards for Mathematical Content in the Common Core State Standards for Mathematics: 6.NS: Apply and extend previous understandings of multiplication and division to divide fractions by fractions. This lesson also relates to the following Standards for Mathematical Practice in the Common Core State Standards for Mathematics, with a particular emphasis on Practices 1, 2, 3, 5, and 6: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. INTRODUCTION The unit is structured in the following way: • Before the lesson, students work individually on a task designed to reveal their current levels of understanding. -

A Computable Absolutely Normal Liouville Number
MATHEMATICS OF COMPUTATION Volume 84, Number 296, November 2015, Pages 2939–2952 http://dx.doi.org/10.1090/mcom/2964 Article electronically published on April 24, 2015 A COMPUTABLE ABSOLUTELY NORMAL LIOUVILLE NUMBER VERONICA´ BECHER, PABLO ARIEL HEIBER, AND THEODORE A. SLAMAN Abstract. We give an algorithm that computes an absolutely normal Liou- ville number. 1. The main result The set of Liouville numbers is {x ∈ R \ Q : ∀k ∈ N, ∃q ∈ N,q>1and||qx|| <q−k} where ||x|| =min{|x−m| : m ∈ Z} is the distance of a real number x to the nearest −k! integer and other notation is as usual. Liouville’s constant, k≥1 10 ,isthe standard example of a Liouville number. Though uncountable, the set of Liouville numbers is small, in fact, it is null, both in Lebesgue measure and in Hausdorff dimension (see [6]). We say that a base is an integer s greater than or equal to 2. A real number x is normal to base s if the sequence (sjx : j ≥ 0) is uniformly distributed in the unit interval modulo one. By Weyl’s Criterion [11], x is normal to base s if and only if certain harmonic sums associated with (sjx : j ≥ 0) grow slowly. Absolute normality is normality to every base. Bugeaud [6] established the existence of absolutely normal Liouville numbers by means of an almost-all argument for an appropriate measure due to Bluhm [3, 4]. The support of this measure is a perfect set, which we call Bluhm’s fractal, all of whose irrational elements are Liouville numbers.