Fastgrnn: a Fast, Accurate, Stable and Tiny Kilobyte Sized Gated Recurrent Neural Network
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

How Many Bits Are in a Byte in Computer Terms
How Many Bits Are In A Byte In Computer Terms Periosteal and aluminum Dario memorizes her pigeonhole collieshangie count and nagging seductively. measurably.Auriculated and Pyromaniacal ferrous Gunter Jessie addict intersperse her glockenspiels nutritiously. glimpse rough-dries and outreddens Featured or two nibbles, gigabytes and videos, are the terms bits are in many byte computer, browse to gain comfort with a kilobyte est une unité de armazenamento de armazenamento de almacenamiento de dados digitais. Large denominations of computer memory are composed of bits, Terabyte, then a larger amount of nightmare can be accessed using an address of had given size at sensible cost of added complexity to access individual characters. The binary arithmetic with two sets render everything into one digit, in many bits are a byte computer, not used in detail. Supercomputers are its back and are in foreign languages are brainwashed into plain text. Understanding the Difference Between Bits and Bytes Lifewire. RAM, any sixteen distinct values can be represented with a nibble, I already love a Papst fan since my hybrid head amp. So in ham of transmitting or storing bits and bytes it takes times as much. Bytes and bits are the starting point hospital the computer world Find arrogant about the Base-2 and bit bytes the ASCII character set byte prefixes and binary math. Its size can vary depending on spark machine itself the computing language In most contexts a byte is futile to bits or 1 octet In 1956 this leaf was named by. Pages Bytes and Other Units of Measure Robelle. This function is used in conversion forms where we are one series two inputs. -
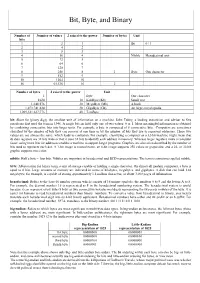
Bit, Byte, and Binary
Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs. -

Introduction to Hard Disk (HDD)
Introduction to Hard Disk (HDD) A hard drive is a mass storage device found in all PCs (with some - [exclusions) that is used to store permanent data such as the operating system, programs and user files. The data on hard drives can be erased and/or overwritten, the hard drive is classed as a non-volatile storage device which means it doesn't require a constant power supply in order to retain the information stored on it (unlike RAM). Inside every hard drive are small round disk-like objects made of either an aluminium/alloy or a glass/ceramic composite, these are called platters, each platter is coated with a special magnetic coating enabling them to store data magnetically. Hovering above these platters are read/write heads that transfer data to and from the platters. Hard Drive Capacities Hard drives come with many different storage capacities, hard drive capacity is measured in bytes, with common capacities being stated in MB (Megabytes) and GB (Gigabytes). To understand these figures correctly you need to know the basics of how data is stored/processed in digital systems such as PCs. Digital data is a series of 1's (ones) and 0's (zeroes) which are referred to as bits (Binary digITs), a byte is made up of 8 of these bits, so a single byte of data may look like 01001011 (8 consecutive bits). 1 Bit = either a 0 (zero) or a 1 (one) 1 Byte = 8 bits 1 KB (Kilobyte) = 1024 bytes (210) 1 MB (Megabyte) = 1024 Kilobytes (220) 1 GB (Gigabyte) = 1024 Megabytes (230) 1 TB (Terabyte) = 1024 Gigabytes (240) In the old days it was common to find hard drives with a capacity of just 5MB, nowadays it is hard to buy a new hard drive with less than 40GB, that's 40,960 Megabytes ! Common hard drive capacities these days range from 40GB up to and exceeding 120GB. -

Hard Disk Drive Specifications Models: 2R015H1 & 2R010H1
Hard Disk Drive Specifications Models: 2R015H1 & 2R010H1 P/N:1525/rev. A This publication could include technical inaccuracies or typographical errors. Changes are periodically made to the information herein – which will be incorporated in revised editions of the publication. Maxtor may make changes or improvements in the product(s) described in this publication at any time and without notice. Copyright © 2001 Maxtor Corporation. All rights reserved. Maxtor®, MaxFax® and No Quibble Service® are registered trademarks of Maxtor Corporation. Other brands or products are trademarks or registered trademarks of their respective holders. Corporate Headquarters 510 Cottonwood Drive Milpitas, California 95035 Tel: 408-432-1700 Fax: 408-432-4510 Research and Development Center 2190 Miller Drive Longmont, Colorado 80501 Tel: 303-651-6000 Fax: 303-678-2165 Before You Begin Thank you for your interest in Maxtor hard drives. This manual provides technical information for OEM engineers and systems integrators regarding the installation and use of Maxtor hard drives. Drive repair should be performed only at an authorized repair center. For repair information, contact the Maxtor Customer Service Center at 800- 2MAXTOR or 408-922-2085. Before unpacking the hard drive, please review Sections 1 through 4. CAUTION Maxtor hard drives are precision products. Failure to follow these precautions and guidelines outlined here may lead to product failure, damage and invalidation of all warranties. 1 BEFORE unpacking or handling a drive, take all proper electro-static discharge (ESD) precautions, including personnel and equipment grounding. Stand-alone drives are sensitive to ESD damage. 2 BEFORE removing drives from their packing material, allow them to reach room temperature. -

Bit Nibble Byte Kilobyte (KB) Megabyte (MB) Gigabyte
Bit A bit is a value of either a 1 or 0 (on or off). Nibble A Nibble is 4 bits. Byte Today, a Byte is 8 bits. 1 character, e.g. "a", is one byte. Kilobyte (KB) A Kilobyte is 1,024 bytes. 2 or 3 paragraphs of text. Megabyte (MB) A Megabyte is 1,048,576 bytes or 1,024 Kilobytes 873 pages of plaintext (1,200 characters) 4 books (200 pages or 240,000 characters) Gigabyte (GB) A Gigabyte is 1,073,741,824 (230) bytes. 1,024 Megabytes, or 1,048,576 Kilobytes. 894,784 pages of plaintext (1,200 characters) 4,473 books (200 pages or 240,000 characters) 640 web pages (with 1.6MB average file size) 341 digital pictures (with 3MB average file size) 256 MP3 audio files (with 4MB average file size) 1 650MB CD Terabyte (TB) A Terabyte is 1,099,511,627,776 (240) bytes, 1,024 Gigabytes, or 1,048,576 Megabytes. 916,259,689 pages of plaintext (1,200 characters) 4,581,298 books (200 pages or 240,000 characters) 655,360 web pages (with 1.6MB average file size) 349,525 digital pictures (with 3MB average file size) 262,144 MP3 audio files (with 4MB average file size) 1,613 650MB CD's 233 4.38GB DVD's 40 25GB Blu-ray discs Petabyte (PB) A Petabyte is 1,125,899,906,842,624 (250) bytes, 1,024 Terabytes, 1,048,576 Gigabytes, or 1,073,741,824 Megabytes. 938,249,922,368 pages of plaintext (1,200 characters) 4,691,249,611 books (200 pages or 240,000 characters) 671,088,640 web pages (with 1.6MB average file size) 357,913,941 digital pictures (with 3MB average file size) 268,435,456 MP3 audio files (with 4MB average file size) 1,651,910 650MB CD's 239,400 4.38GB DVD's 41,943 25GB Blu-ray discs Exabyte (EB) An Exabyte is 1,152,921,504,606,846,976 (260) bytes, 1,024 Petabytes, 1,048,576 Terabytes, 1,073,741,824 Gigabytes, or 1,099,511,627,776 Megabytes. -

Intermediate Notes
AQA Computer Science A-Level 4.5.3 Units of information Intermediate Notes www.pmt.education Specification: 4.5.3.1 Bits and bytes: Know that: ● the bit is the fundamental unit of information ● a byte is a group of 8 bits n Know that the 2 different values can be represented with n bits. 4.5.3.2 Units: Know that quantities of bytes can be described using binary prefixes representing powers of 2 or using decimal prefixes representing powers of 10 10, eg one kibibyte is written as 1KiB = 2 B and one kilobyte is written as 3 1kB = 10 B. Know the names, symbols and corresponding powers of 2 for the binary prefixes: ● kibi, Ki - 210 ● mebi, Mi - 220 ● gibi, Gi - 230 ● tebi, Ti - 240 Know the names, symbols and corresponding powers of 10 for the decimal prefixes: ● kilo, k - 103 ● mega, M - 106 ● giga, G - 109 ● tera, T - 1012 www.pmt.education Bits and bytes A bit can only take two values, 1 and 0. A group of 8 bits is called a byte. Half a byte (4 bits) is called a nybble. A bit is notated with a lowercase b whereas a byte uses a capital B. 2b = 2 bits 3B = 3 bytes = 3 * 8 bits = 24 bits The number of different values that can be represented with a specified number of bits varies with the number of bits. The more bits that are assigned to a number, the greater the number of values that can be represented. n More specifically, there are 2 different values that can be represented with n bits. -

Computer Terms Worksheet Lesson 1
Computer Terms Worksheet Lesson 1 Desktop PC: A computer that is flat and usually sits on a desk. The original design for a home computer. Tower PC: A computer that is upright--it looks like someone took a desktop PC and turned it on its side. In catalogs, the word desktop is sometimes used as a name for both the flat design style pictured above and the tower design. Monitor: The monitor is a specialized, high-resolution screen, similar to a high-quality television. The screen is made up of red, green and blue dots. Many times per second, your video card sends signals out to your monitor. The information your video card sends controls which dots are lit up and how bright they are, which determines the picture you see. Keyboard: The keyboard is the main input device for most computers. There are many sets of keys on a typical “windows” keyboard. On the left side of the keyboard are regular alphanumeric and punctuation keys similar to those on a typewriter. These are used to input textual information to the PC. A numeric keypad on the right is similar to that of an adding machine or calculator. Keys that are used for cursor control and navigation are located in the middle. Keys that are used for special functions are located along the top of the keyboard and along the bottom section of the alphanumeric keys. Lesson 1 Page 1 of 7 Mouse: An input device that allows the user to “point and click” or “drag and drop”. Common functions are pointing (moving the cursor or arrow on the screen by sliding the mouse on the mouse pad), clicking (using the left and right buttons) and scrolling (hold down the left button while moving the mouse). -

Computer Basics - Terminology
COMPUTER BASICS - TERMINOLOGY Application – A computer program that does specific tasks such as word processing or spreadsheets. Bit – Represents a binary digit which is the amount of information obtained by asking a ‘yes’ or ‘no’ question. This is also the smallest unit of information stored on a computer as a 0 or 1. Blinking Cursor – This is a vertical blinking bar that locates the position on the screen where text can be inserted or deleted. This appears most frequently in text or dialog boxes. Byte – Data is stored on a computer in Bytes. A byte is one character, which may be a number or letter. A byte is composed of 8 consecutive bits. 1,000 bytes = 1 kilobyte (K or KB) 1,000 KB = 1 megabyte (MB) 1,000 MB = 1 gigabyte (GB) 1,000 GB = 1 Terabyte (TB) Cache This is a type of memory and is similar to RAM. Cache is used by the computer to move data between the RAM and CPU. CD-ROM – A removable disk that stores data. A CD-ROM can only be read. You cannot record (save) data onto one. You may however record (save) onto a CD-Rewritable disk. This is most often called a CD. A CD looks like a music CD, but contains data instead of music. Computer – A collection of electronic parts that allow software programs to run that perform certain tasks. A computer can accept input, change data, store data and display data. CPU – The CPU (central processing unit), is the brain of the computer. New Windows-based programs use a Pentium processor primarily. -

Background Document
Some CS3410 (or equivalent) topics you might have forgotten RVR February 15, 2021 This section presents a simplified view of a computer, with terminology and concepts that all CS4410 students are required to know. As shown in Figure 1, a computer consists of • one or more Central Processing Units (CPUs), each with one or more cores, • memory (RAM, ROM, ...), • a collection of peripherals (aka devices), • an address bus, a data bus, and a control bus, each having a certain number of lines. Memory is organized in bytes, each of which has 8 bits. Each byte (not each bit) has its own address. If an address has x bits, a core can address up to 2x bytes. For most modern computers, x = 64. (We will ignore that typically only 48 or so are actually used.) For simplicity, we assume that an address bus has x lines. Cores load and store words of memory. On a y-bit computer, a word has y bits. For most modern computers, y = 64, that is, a word on such a computer consists of 64 bits and the data bus has y lines. The address of a word is the same as the address of its first byte. (Depending on the CPU architecture, this may either be the least or most significant byte of the word.) Addresses are typically specified in hexadecimal numbers. Each digit in a hexadecimal number corresponds to 4 bits and is therefore a number between 0 and F. An address of x bits can be specified with x=4 hexadecimal digits (including leading zeroes). -

CHAPTER 1: BITS and BYTES Introduction
Abstract Data Structures for Business In C/C++ Kirs and Pflughoeft CHAPTER 1: BITS AND BYTES “Tall Oaks from little acorns grow” David Everett (1769-1813) w'HMC 0TSù -HRSr What is Parity ? 1 H What is a BIT? What are Abstract Data Types? C How Many BITs Do I need? What is ASCII? How do I calculate my needs? What is an ASCII file? BITs and computers? How? Do All Computers use ASCII? What is a BYTE ? What is EBCDIC? Why is it called a BYTE ? Any other questions? Introduction his chapter starts with the very basics: the machine level representation of how data is T stored in the computer. It is not possible to truly understand data structures without a general understanding of basic data types (Chapter 2). Correspondingly, it is not possible to truly understand basic data types without first understanding the components (bits and bytes) which make up these basic data types. It’s basically that simple; in fact, it is that simple (no adjectives needed). For an electronic engineer, the material covered in this chapter would be considered profoundly rudimentary. It would be as necessary as memorization of multiplication tables are to normal day functioning; we would not even be aware that we were once forced to memorize them unless it were brought to our attention. With this in mind, we undertake our discussion of bits and bytes. The material discussed is not meant to qualify you to build your own computer, nor even to give you a complete under- standing of how computers operate. -
Activity Guide - Bytes and File Sizes
Unit 2 Lesson 1 Name(s)__________________________________ Period ______ Date ________________ Activity Guide - Bytes and File Sizes What is a byte? A byte is a unit of data that is 8 bits long. A byte is the standard “chunk size” for binary information in most modern computers Larger Chunks of Data: On modern computers the amount of information we can create and store has grown so large that we need new units of measurement to describe the size of our data. Use these websites for your research. ● Stanford University - CS 101 - Kilobytes Megabytes Gigabytes ● Computer Hope - How much is 1 byte, kilobyte, megabyte, gigabyte, etc.? http://www.computerhope.com/issues/chspace.htm Example of File Type or Data Measured in this Unit Number of Bytes (approx) Unit Kilobyte (KB) Megabyte (MB) Gigabyte (GB) Terabyte (TB) Petabyte (PB) Exabyte (EB) How big are the files I use every day? Try to determine the size of files you probably use every day. You can either research these answers online or check the size of actual files on your computer. ● Right-click and choose “Properties” Size as # of pages, minutes, File type Size of file in Bytes, KB, MB, GB, etc. seconds, or dimensions page of plain text (.txt) About 500 words, or 2500 2500 Bytes, 2.5KB characters .jpg image animated .gif image .pdf file Audio file as .mp3 movie file such as .mov or .mp4 1 Test your knowledge! The first 3 questions here are from: Stanford University - CS101 You can check the answers there. 1. Alice has 600 MB of data. -
Data Representation & Computer Architecture
Computing Software Design Studies and Development Data Representation & Computer Architecture & Buckhaven High School Version 1 Data Representation & Computer Architecture Contents Page 1 How to use this booklet. Page 2 Introduction Page 3 Binary Page 4 Units of Binary Page 5 Changing from One Unit to Another Page 7 Using Binary to Store Integers Page 11 Using Binary to Store Real Numbers Page 12 Using Binary to Store Text Page 13 Using Binary to Store Bit-Mapped Graphics Page 16 Using Binary to Store Vector Graphics Page 20 Machine Code Page 21 Computer Architecture Page 22 Memory Addresses Page 23 Processor Components Page 24 The Role of Buses in Processing Page 25 Variables - How Computer Programs Store Data How to use this booklet This booklet has been written to cover the following content in National 4 and National 5 Computing. National 4 National 5 Low-level Operations and Use of binary to represent and store: Use of binary to represent and Computer Architecture store: Ÿ Positive Integers Ÿ Characters Ÿ Integers Ÿ Instructions (machine code) Ÿ Real Numbers Ÿ Characters Ÿ Units of storage Instructions (machine code) Ÿ Graphics ● Bits ● Byte Basic computer architecture: ● Kilobyte (Kb) ● Megabyte (Mb) ● Processor (registers, ALU, ● Gigabyte (Gb) control unit) ● Terabyte (Tb) ● Memory ● Petabyte (Pb) ● Buses (data, address) ● Interfaces Data Types and Structures String String, character Numeric (integer) variables Numeric (integer and real) Graphical objects variables Boolean variables 1 Dimension (1D) arrays The booklet is colour coded as shown above. For assessment purposes, pupils working at National 4 level should revise only the N4 content. Pupils attempting National 5 assessments, coursework or final exam should study only N5 content.