Rewriting Modulo Isotopies in Pivotal Linear $(2, 2) $-Categories
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

MAX3946 1Gbps to 11.3Gbps, SFP+ Laser Driver with Laser Impedance
19-5182; Rev 1; 5/11 EVALUATION KIT AVAILABLE 1Gbps to 11.3Gbps, SFP+ Laser Driver with Laser Impedance Mismatch Tolerance MAX3946 General Description Features The MAX3946 is a +3.3V, multirate, low-power laser S 225mW Power Dissipation Enables < 1W SFP+ diode driver designed for Ethernet and Fibre Channel Modules transmission systems at data rates up to 11.3Gbps. S Up to 100mW Power Consumption Reduction by This device is optimized to drive a differential transmit- Enabling the Use of Unmatched FP/DFB TOSAs ter optical subassembly (TOSA) with a 25I flex circuit. The unique design of the output stage enables use of S Supports SFF-8431 SFP+ MSA and SFF-8472 unmatched TOSAs, greatly reducing headroom limita- Digital Diagnostic tions and lowering power consumption. S 225mW Power Dissipation at 3.3V (IMOD = 40mA, The device receives differential CML-compatible signals IBIAS = 60mA Assuming 25I TOSA) with on-chip line termination. It can deliver laser modula- S Single +3.3V Power Supply tion current of up to 80mA, at an edge speed of 22ps S Up to 11.3Gbps (NRZ) Operation (20% to 80%), into a 5I to 25I external differential load. S Programmable Modulation Current from 10mA to The device is designed to have a symmetrical output 100mA (5I Load) stage with on-chip back terminations integrated into its outputs. A high-bandwidth, fully differential signal S Programmable Bias Current from 5mA to 80mA path is implemented to minimize deterministic jitter. An S Programmable Input Equalization equalization block can be activated to compensate for S Programmable Output Deemphasis the SFP+ connector. -

CP/M-80 Kaypro
$3.00 June-July 1985 . No. 24 TABLE OF CONTENTS C'ing Into Turbo Pascal ....................................... 4 Soldering: The First Steps. .. 36 Eight Inch Drives On The Kaypro .............................. 38 Kaypro BIOS Patch. .. 40 Alternative Power Supply For The Kaypro . .. 42 48 Lines On A BBI ........ .. 44 Adding An 8" SSSD Drive To A Morrow MD-2 ................... 50 Review: The Ztime-I .......................................... 55 BDOS Vectors (Mucking Around Inside CP1M) ................. 62 The Pascal Runoff 77 Regular Features The S-100 Bus 9 Technical Tips ........... 70 In The Public Domain... .. 13 Culture Corner. .. 76 C'ing Clearly ............ 16 The Xerox 820 Column ... 19 The Slicer Column ........ 24 Future Tense The KayproColumn ..... 33 Tidbits. .. .. 79 Pascal Procedures ........ 57 68000 Vrs. 80X86 .. ... 83 FORTH words 61 MSX In The USA . .. 84 On Your Own ........... 68 The Last Page ............ 88 NEW LOWER PRICES! NOW IN "UNKIT"* FORM TOO! "BIG BOARD II" 4 MHz Z80·A SINGLE BOARD COMPUTER WITH "SASI" HARD·DISK INTERFACE $795 ASSEMBLED & TESTED $545 "UNKIT"* $245 PC BOARD WITH 16 PARTS Jim Ferguson, the designer of the "Big Board" distributed by Digital SIZE: 8.75" X 15.5" Research Computers, has produced a stunning new computer that POWER: +5V @ 3A, +-12V @ 0.1A Cal-Tex Computers has been shipping for a year. Called "Big Board II", it has the following features: • "SASI" Interface for Winchester Disks Our "Big Board II" implements the Host portion of the "Shugart Associates Systems • 4 MHz Z80-A CPU and Peripheral Chips Interface." Adding a Winchester disk drive is no harder than attaching a floppy-disk The new Ferguson computer runs at 4 MHz. -

Week 49, 2018 – Friday 7Th December Click Here to View the Email As a PDF
Shipping Regulations and Guidance Week 49, 2018 – Friday 7th December Click Here to view the email as a PDF. Forward this email to a friend Flag State Regulations and Guidance Updates UK – has released a new marine guidance notice entitled 'ILO Work in Fishing Convention, 2007 (No. 188) – Fishermen's Work Agreements'. Australia – has released an amendment order to marine order 'Certificates of survey - national law'. Marshall Islands – has published a new marine safety advisory entitled 'Guidance on the Development of a Ship Implementation Plan for the Consistent Implementation of the 0.50% Sulphur Limit under MARPOL Annex VI'. Panama – has updated three circulars: 'Ballast Water Management Convention 2004, Panama Policy' 'Adoption of Amendments to MARPOL 73/78, Annex VI Panama Policy on IMO- DCS scheme'. 'Correction of Deficiencies found in ASI InspectionsCorrection of Deficiencies found in ASI Inspections'. Isle of Man – has issued a new shipping notice entitled 'SOLAS Chapter XI-2 & the ISPS Code'. Singapore – has released a new port marine circular entitled 'Johor Bahru Port Limits'. Recent Class Society Guidance American Bureau of Shipping – has released a new guidance document entitled 'Guide for Enhanced Shaft Alignment', and has updated seven collections of documents: 'Guide for Building and Classing International Naval Ships' 'Rules for Building and Classing Offshore Support Vessels' 'Rules for Building and Classing High-Speed Naval Craft' 'Rules for Building and Classing Mobile Offshore Drilling Units' 'Rules for Building and Classing High-Speed Craft' 'Rules for Building and Classing Steel Vessels' 'Rules for Building and Classing Steel Vessels Under 90 Meters in Length'. Bureau Veritas – has has issued a new guidance document entitled 'Rules for the Classification of Diving Systems'. -

Data Transfer Node (DTN) Tests on the GÉANT Testbeds Service (GTS)
09-12-2020 Data Transfer Node (DTN) Tests on the GÉANT Testbeds Service (GTS) Grant Agreement No.: 856726 Work Package WP6 Task Item: Task 2 Document ID: GN4-3-20-265f683 Authors: Iacovos Ioannou (CYNET), Damir Regvart (CARNET), Joseph Hill (UvA/SURF), Maria Isabel Gandia (CSUC/RedIRIS), Ivana Golub (PSNC), Tim Chown (Jisc), Susanne Naegele Jackson (FAU/DFN) © GÉANT Association on behalf of the GN4-3 project. The research leading to these results has received funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 856726 (GN4-3). Abstract Many research projects need to transfer large amounts of data and use specialised Data Transfer Nodes (DTNs) to optimise the efficiency of these transfers. In order to help NRENs to better support user communities who seek to move large volumes of data across their network, a DTN Focus Group was set up in the Network Technologies and Services Development work package (WP6) of the GN4-3 project, which has performed several activities around DTN deployment, the results of which are summarised in this document. Table of Contents Executive Summary 1 1 Introduction 2 2 The DTN Survey and DTN Wiki 5 3 Optimising DTN Configurations 6 3.1 Networking 6 3.1.1 Socket Parameters 7 3.1.2 TCP Socket Parameters 7 3.1.3 NIC Driver Settings 8 3.1.4 MTU Settings 8 3.2 Storage 9 3.2.1 Bus vs Disk Speed 9 3.2.2 Spinning versus Solid State Disks 9 3.2.3 NVMe 9 3.2.4 RAID 10 3.2.5 Remote Storage 10 3.3 Architecture 10 3.3.1 Fast Cores vs Many Cores 10 3.3.2 NUMA 10 3.3.3 -
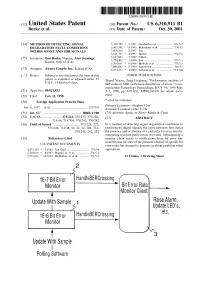
Update W Sample Polling Software U.S
USOO6310911B1 (12) United States Patent (10) Patent No.: US 6,310,911 B1 Burke et al. (45) Date of Patent: Oct. 30, 2001 (54) METHOD OF DETECTING SIGNAL 5,418,789 5/1995 Gersbach et al. ..................... 371/5.2 DEGRADATION FAULT CONDITIONS 5,467,341 11/1995 Matsukane et al. ................... 370/17 WITHIN SONET AND SDH SIGNALS 5,606,563 2/1997 Lee. 5,621,737 * 4/1997 Bucher .................................. 371/5.1 (75) Inventors: panist, Nips Alan Jennings, 5,724,3625,627,837 3/19985/1997 Gillett.Lau ....................................... 371/5.1 s 5,764,651 * 6/1998 Bullock et al. .. ... 371/5.5 rr. A 5,886,842 * 3/1999 Ziperovich ...... ... 360/51 (73) Assignee: Alcatel Canada Inc., Kanata (CA) 6,073,257 * 4/2000 Labonte et al. ...................... 714/704 (*) Notice: Subject to any disclaimer, the term of this OTHER PUBLICATIONS patent is extended or adjusted under 35 Zhand Xiaoru, Zneg Lieguang: "Performance analysis of U.S.C. 154(b) by 0 days. BIP codes in SDH on Poisson distribution of errors.” Com munication Technology Proceedings, ICCT '96, 1996 May (21) Appl. No.: 09/021,833 5–7, 1996, pp. 829–832, XP002146479 the whole docu (22) Filed: Feb. 11, 1998 ment. (30) Foreign Application Priority Data * cited by examiner Primary Examiner Stephen Chin Feb. 11, 1997 (CA) .................................................. 2197263 ASSistant Examiner-Dac V. Ha (51) Int. Cl." ................................................. H04B 17700 (74) Attorney, Agent, or Firm Marks & Clerk (52) U.S. Cl. .......................... 375/224; 375/227; 375/228; (57) ABSTRACT 714/48; 714/704; 370/241; 370/242 (58) Field of Search .................................... -

Linux Commands Cheat Sheet
LINUX COMMANDS CHEAT SHEET by Gokhan Kosem, www.ipcisco.com System Information Commands User Information Commands shows user&group ids of the current uname -a shows Linux system info id user uname -r shows kernel release info last shows the last users logged on cat /etc/redhat-release shows installed redhat version whoami shows who you are logged in as uptime displays system running/life time who shows who is logged into the system shows who is logged in and what hostname shows system host name w they do hostname -I shows ip addresses of the host groupadd test creates group “test” creates “Gokhan” account with last reboot displays system reboot history useradd -c “GK” -m Gokhan comment “GK” date displays current date and time userdel Gokhan deletes account “Gokhan” usermod -aG Networkers adds account “Gokhan” to the cal displays monthly calendar Gokhan “Networkers” group mount shows mounted filesy-stems File Permission changes ownership of a File Commands chown user file/directory shows file type and access changes user and group for a file or ls -l chown user:group filename permission directory ls -a lists also hidden files r (read) permission, 4 ls -al lists files and directories detailly w (write) permission, 2 File Permissions pwd shows present directory x (execute) permission, 1 mkdir directory creates a directory -= no permission rm xyz deletes file xyz File Owner owner/group/everyone deletes directory /xyz and its 777 | Owner, Group, Everyone has rm -r /xyz contents recursively rwx permissions forcefully deletes abc file without -

The Beta Marshall-Olkin Family of Distributions Morad Alizadeh1, Gauss M
Alizadeh et al. Journal of Statistical Distributions and Applications (2015) 2:4 DOI 10.1186/s40488-015-0027-7 METHODOLOGY Open Access The beta Marshall-Olkin family of distributions Morad Alizadeh1, Gauss M. Cordeiro2, Edleide de Brito3* and Clarice Garcia B. Demétrio4 *Correspondence: [email protected] Abstract 3 Departamento de Estatística, We study general mathematical properties of a new generator of continuous Universidade Federal da Bahia, Salvador, Bahia, Brazil distributions with three extra shape parameters called the beta Marshall-Olkin family. Full list of author information is We present some special models and investigate the asymptotes and shapes. The new available at the end of the article density function can be expressed as a mixture of exponentiated densities based on the same baseline distribution. We derive a power series for its quantile function. Explicit expressions for the ordinary and incomplete moments, quantile and generating functions, Bonferroni and Lorenz curves, Shannon and Rényi entropies and order statistics, which hold for any baseline model, are determined. We discuss the estimation of the model parameters by maximum likelihood and illustrate the flexibility of the family by means of two applications to real data. PACS: 02.50.Ng, 02.50.Cw, 02.50.-r Mathematics Subject Classification (2010): 62E10, 60E05, 62P99 Keywords: Generated family; Marshall-Olkin family; Maximum likelihood; Moment; Order statistic; Quantile function; Rényi entropy 1 Introduction Recently, some attempts have been made to define new families to extend well-known distributions and at the same time provide great flexibility in modelling data in practice. So, several classes by adding one or more parameters to generate new distributions have been proposed in the statistical literature. -

DNVGL-RU-SHIP-Pt6ch9 Survey Requirements
RULES FOR CLASSIFICATION Ships Edition October 2015 Part 6 Additional class notations Chapter 9 Survey requirements The content of this service document is the subject of intellectual property rights reserved by DNV GL AS ("DNV GL"). The user accepts that it is prohibited by anyone else but DNV GL and/or its licensees to offer and/or perform classification, certification and/or verification services, including the issuance of certificates and/or declarations of conformity, wholly or partly, on the basis of and/or pursuant to this document whether free of charge or chargeable, without DNV GL's prior written consent. DNV GL is not responsible for the consequences arising from any use of this document by others. The electronic pdf version of this document, available free of charge from http://www.dnvgl.com, is the officially binding version. DNV GL AS FOREWORD DNV GL rules for classification contain procedural and technical requirements related to obtaining and retaining a class certificate. The rules represent all requirements adopted by the Society as basis for classification. © DNV GL AS October 2015 Any comments may be sent by e-mail to [email protected] If any person suffers loss or damage which is proved to have been caused by any negligent act or omission of DNV GL, then DNV GL shall pay compensation to such person for his proved direct loss or damage. However, the compensation shall not exceed an amount equal to ten times the fee charged for the service in question, provided that the maximum compensation shall never exceed USD 2 million. -

CSX700 Floating Point Processor Datasheet
CSX700 Floating Point Processor Datasheet Feature summary 1.2V and 1.8V analog supplies High performance Mechanical/thermal 40 mm x 40 mm thermally enhanced flip-chip 96 GFLOPS double precision floating point package (peak) 1429 balls on 1 mm pitch Single and double precision, IEEE 754 compliant, FPUs 680 signal pins (including analog supplies) Power efficient architecture Power dissipation 10W typical Features Description Professional Software Development Kit (SDK) The CSX700 is a high performance, low power Two multi-threaded processing cores, each floating point coprocessor. It is designed for use with: in a variety of applications in high performance – Array of 96 Processing Elements (PE) computing and embedded systems. – Double and single precision floating-point The CSX700 is the second product in acceleration in every PE ClearSpeed’s family of floating point application – Controller with 8 Kbyte instruction and 4 accelerators. The CSX processors are based Kbyte data cache around ClearSpeed’s multi-threaded array PCI-Express x16 (Gen. 1 rev 1.1) host processor (MTAP) architecture. This architecture interface has been developed to address the 2 x 128 Kbyte on-chip SRAM implementation issues of high-performance systems by providing unparalleled performance- 2 x 8 Gbytes of external DDR2 DRAM support per-watt. High speed chip-chip interface (CCBR) Configuration/debug port (HDP) CSX700 Bus Bus JTAG boundary scan (IEEE compliant) Monitor Monitor 128K 128K Applications SRAM SRAM MU MTAP MTAP MU Designed for data-intensive and high-compute DDR2- DDR2- applications 533 533 Finance Radar systems D D M M Bio-informatics A A Signal processing On Chip Network (ClearConnect Bus) Medical imaging System DM A Host Interface Services PCIe x16 Electrical HDP CCBR 1.0V core supply 1.8V and 3.3V I/O supplies 06-PD-1425 Rev 1E January 2011 1 Table of contents CSX700 Datasheet Table of contents 1 Description . -

Blockmon – Block Monitor Longmon – Long Monitor Leafmon – Leaf Monitor
BlockMon – Block Monitor LongMon – Long Monitor LeafMon – Leaf Monitor • Bypass range 2.2V to 5.0V. • Bypass current 0A to 2A (typically 1A). • Over-voltage protection up to ±20V. • Noise immune opto-isolated. • Cell temperature and bypass load temperature measurements. • Monitoring of live individual cell parameters and remote cell diagnostics. • Covered in black thermally conductive epoxy (robust). • Red and green LEDs for diagnostics and status. • Parameters fully remotely programmable and software is upgradeable. BlockMon For “block” prism (Block type cells. Monitor) M8 and M14 bolt sizes. LongMon For long cylindrical or pouch (Long type cells. Monitor) LeafMon (Leaf cell For Leaf Cells (2s) monitor) (contains 2 GenMon cell monitors) Note: BlockMon, LongMon and LeafMons are referred to collectively as “CellMon” BlockMon, LongMon and LeafMons are intelligent Power is obtained with a separate positive and battery monitor systems used to maintain high negative cable. All units use the same circuit and power lithium cell batteries at peak performance connectors. They are fully interchangeable except and optimum parameter range. They provide live for the addition of the extra negative wire on the 4 cell status with programmable over-charge voltage pin connector (for LongMon). The terminology limiting, shunting power up to 2A (7W with fan “CellMon” is used when referring to either cooling) or typically 1A of bypass without cooling BlockMon or LongMon or GenMon on each end of with 3.65V limit. the LeafMon. BlockMon is attached to the negative battery The primary function is to limit cell over-voltage by terminal with positive battery power via a cable. applying a variable bypass current across each LongMon is used for cylindrical type batteries and cell. -

Wolfson WM9715L Audio Codec and Touch Screen Controller
w WM9715L AC’97 Audio and Touchpanel CODEC DESCRIPTION FEATURES The WM9715L is a highly integrated input / output device AC’97 Rev 2.2 compatible stereo CODEC designed for mobile computing and communications. The - DAC SNR 90dB, THD –86dB device can connect directly to a 4-wire or 5-wire touchpanel, - ADC SNR 88dB, THD –88dB mono or stereo microphones, stereo headphones and a - Variable Rate Audio, supports all WinCE sample rates mono speaker, reducing total component count in the - Tone Control, Bass Boost and 3D Enhancement system. Additionally, phone input and output pins are On-chip 45mW headphone driver provided for seamless integration with wireless On-chip 400mW mono speaker driver communication devices. Stereo, mono or differential microphone input - Automatic Level Control (ALC) The WM9715L also offers up to four auxiliary ADC inputs for Auxiliary mono DAC (ring tone or DC level generation) analogue measurements such as temperature or light. To Seamless interface to wireless chipset monitor the battery voltage in portable systems, the Resistive touchpanel interface WM9715L has two uncommitted comparator inputs. - Supports 4-wire and 5-wire panels All device functions are accessed and controlled through a - 12-bit resolution, INL 3 LSBs (<0.5 pixels) single AC-Link interface compatible with the AC’97 standard - X, Y and touch-pressure (Z) measurement (rev 2.2). Additionally, the WM9715L can generate interrupts - Pen-down detection supported in Sleep Mode to indicate pen down, pen up, availability of touchpanel data, 2 comparator inputs for battery monitoring Up to 4 auxiliary ADC inputs low battery, and dead battery. 1.8V to 3.6V supplies The WM9715L operates at supply voltages from 1.8 to 3.6 7x7mm QFN Volts. -

Bmon Documentation Release 0.0.1
bmon Documentation Release 0.0.1 Alan Mitchell Sep 27, 2021 Users 1 User Introduction 3 2 System Administrator Introduction5 3 Developer Introduction 7 4 Contact Information 9 4.1 User Introduction.............................................9 4.2 System Administrator Introduction................................... 10 4.3 How to Install BMON on a Web Server................................. 13 4.4 How to Install BMON on a Local Web Server.............................. 18 4.5 Add Buildings and Sensors....................................... 27 4.6 Sharing BMON across Multiple Organizations............................. 40 4.7 Setting Up Sensors to Post to BMON.................................. 41 4.8 Multi-Building Charts.......................................... 60 4.9 Sensor Alerts............................................... 68 4.10 Creating a Dashboard.......................................... 74 4.11 Transform Expressions.......................................... 76 4.12 Calculated Fields............................................. 80 4.13 Periodic Scripts.............................................. 92 4.14 How to Create Custom Jupyter Notebook Reports........................... 107 4.15 Custom Reports............................................. 108 4.16 Backing Up and Analyzing Data from the System........................... 111 4.17 System Performance with High Loading................................ 113 4.18 Using CSV Transfer........................................... 115 4.19 Developer Introduction.........................................