Flow Through a Throttle Body a Comparative Study of Heat Transfer, Wall Surface Roughness and Discharge Coefficient
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Small Engine Parts and Operation
1 Small Engine Parts and Operation INTRODUCTION The small engines used in lawn mowers, garden tractors, chain saws, and other such machines are called internal combustion engines. In an internal combustion engine, fuel is burned inside the engine to produce power. The internal combustion engine produces mechanical energy directly by burning fuel. In contrast, in an external combustion engine, fuel is burned outside the engine. A steam engine and boiler is an example of an external combustion engine. The boiler burns fuel to produce steam, and the steam is used to power the engine. An external combustion engine, therefore, gets its power indirectly from a burning fuel. In this course, you’ll only be learning about small internal combustion engines. A “small engine” is generally defined as an engine that pro- duces less than 25 horsepower. In this study unit, we’ll look at the parts of a small gasoline engine and learn how these parts contribute to overall engine operation. A small engine is a lot simpler in design and function than the larger automobile engine. However, there are still a number of parts and systems that you must know about in order to understand how a small engine works. The most important things to remember are the four stages of engine operation. Memorize these four stages well, and everything else we talk about will fall right into place. Therefore, because the four stages of operation are so important, we’ll start our discussion with a quick review of them. We’ll also talk about the parts of an engine and how they fit into the four stages of operation. -

Not for Reproduction
use back code C BRIGGS & STRATTON CORPORATION 1 2 16 3 718 46 615 Illustrated Parts List 404 VERTICAL CRANKSHAFT SHORT BLOCK ASSEMBLIES 616 792738, 792739, 792740, 792741, 792742, 792743 22 51 For use on Engine Model Series 120K00, 121K00, 122K00, 122L00, 146 163 9 123J00, 123K00, 124K00, 124L00, 741 125K00,126L00, 127H00, 128H00, 617 128L00, 129H00 7 668 842 INSTRUCTIONS 883 To obtain the correct part numbers for an engine 869 45 40 4 which has been rebuilt with a Short Block Assem- 870 36 524 bly, follow these instructions: 871 868 45 684 12 A. For all parts shown in the illustrated view to the 40 28 33 left, use this Parts List. 35 584 B. For all other parts, refer to the Illustrated Parts 34 List which is appropriate for your engine by 27 Model, Type and Code (Serial) Number. 585 TO INSTALLER: GIVE THIS PARTS LIST TO 25 27 CUSTOMER AFTER SHORT BLOCK INSTALLATION. 43 51A 15 20 THIS IPL IS SPECIFIC TO THE SHORT 29 BLOCK(S) LISTED. RETAIN FOR FUTURE PARTS REFERENCE. 26 32 32A REF. PART REF. PART REF. PART NO. NO. DESCRIPTION NO. NO. DESCRIPTION NO. NO. DESCRIPTION 1 697322 Cylinder Assembly 25 797302 Piston Assembly 524 692296 Seal−Dipstick Tube 2 399269 Kit−Bushing/Seal (Mag- (Standard) 585 691879 Gasket−Breather Passage neto Side) for 797303 Piston Assembly 615 690340 Retainer−Governor Shaft 3 299819s Seal−Oil (.020” Oversize) 616 698801 Crank−Governor (Magneto Side) 26 797304 Ring Set (Standard) 617 270344s Seal−O Ring 4 493279 Sump−Engine 797305 Ring Set (Intake Manifold) −−−−−−− Note −−−−− (.020” Oversize) 668 493823 Spacer 696294 -

Banks Ram-Air® Intake System
Banks Ram-Air® Intake System 1997-2006 Jeep 4.0L THIS MANUAL IS FOR USE WITH KITS 41816 Gale Banks Engineering 546 Duggan Avenue • Azusa, CA 91702 (626) 969-9600 • Fax (626) 334-1743 Product Information & Sales: (888) 635-4565 bankspower.com ©2009 Gale Banks Engineering 02/17/09 PN 96575 v.3.0 General Installation Practices 5. Route and tie wires and hoses Dear Customer, a minimum of 6 inches away from If you have any questions exhaust heat, moving parts and sharp concerning the installation of edges. Clearance of 8 inches or more your Banks Ram-Air System, is recommended where possible. please call our Technical Service 6. During installation, keep the Hotline at (888) 839-2700 work area clean. If foreign debris between 7:00 am and 5:00 pm is transferred to any Banks system (PT). If you have any questions component, clean it thoroughly before relating to shipping or billing, installing. please contact our Customer Service Department at 7. When raising the vehicle, support (888) 839-5600. it on properly weight-rated safety stands, ramps or a commercial hoist. Thank you.1 Follow the manufacturer’s safety precautions. Take care to balance the vehicle to prevent it from slipping or 1. For ease of installation of your falling. When using ramps, be sure the Banks Ram-air intake system, front wheels are centered squarely on familiarize yourself with the procedure the topsides; put the transmission in by reading the entire manual before park; set the parking brake; and place starting work. This manual contains blocks behind the rear wheels. -
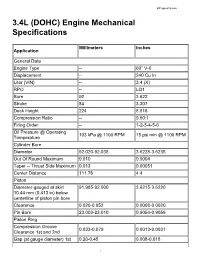
3.4L (DOHC) Engine Mechanical Specifications
60DegreeV6.com 3.4L (DOHC) Engine Mechanical Specifications Millimeters Inches Application General Data Engine Type -- 60° V-6 Displacement -- 240 Cu In Liter (VIN) -- 3.4 (X) RPO -- LQ1 Bore 92 3.622 Stroke 84 3.307 Deck Height 224 8.818 Compression Ratio -- 9.50:1 Firing Order -- 1-2-3-4-5-6 Oil Pressure @ Operating 103 kPa @ 1100 RPM 15 psi min @ 1100 RPM Temperature Cylinder Bore Diameter 92.020-92.038 3.6228-3.6235 Out Of Round Maximum 0.010 0.0004 Taper -- Thrust Side Maximum 0.013 0.00051 Center Distance 111.76 4.4 Piston Diameter-gauged at skirt 91.985-92.000 3.6215-3.6220 10.44 mm (0.413 in) below centerline of piston pin bore Clearance 0.020-0.052 0.0008-0.0020 Pin Bore 23.003-23.010 0.9056-0.9059 Piston Ring Compression Groove 0.033-0.079 0.0013-0.0031 Clearance 1st and 2nd Gap (at gauge diameter) 1st 0.20-0.45 0.008-0.018 1 60DegreeV6.com Gap (at gauge diameter) 2nd 0.56-0.81 0.022-0.032 Oil Groove Clearance 0.028-0.206 0.0011-0.0081 Gap (segment at gauge 0.25-0.76 0.0098-0.0299 diameter) Tension 1st 27.6 N 6.2 lbs Tension 2nd 19.8 N 4.5 lbs Tension Oil 31.2 N 7.0 lbs Piston Pin Diameter 22.9915-22.9964 0.9052-0.9054 Clearance 0.0066-0.0185 0.00026-0.00073 Fit In Rod 0.0165-0.0464 0.0006-0.0018 Crankshaft Main Journal Diameter-All 67.239-67.257 2.6472-2.6479 Taper-Maximum 0.005 0.0002 Out Of Round-Maximum 0.005 0.0002 Cylinder Block Main Bearing 72.155-72.168 2.8407-2.8412 Bore Diameter Crankshaft Main Bearing Inner 67.289-67.316 2.6492-2.6502 Diameter Main Bearing Clearance 0.019-0.064 0.0008-0.0025 Main Thrust Bearing Clearance -

AREVA Design Control Document Rev. 4
U.S. EPR FINAL SAFETY ANALYSIS REPORT 9.5.8 Diesel Generator Air Intake and Exhaust System The diesel generator air intake and exhaust system (DGAIES) provides the diesel engine with combustion air from the outside. The combustion air passes through a filter, silencer, and heater before being compressed by a turbocharger and cooled by the coolant system before entering the individual cylinders for combustion. The exhaust gas system collects the exhaust gas from the individual cylinders and conveys them via the engine-mounted turbocharger, emissions equipment, and an exhaust gas silencer to the outside. 9.5.8.1 Design Basis The design of the system and EPGB establishes that the arrangement and location of the combustion air intake and exhaust gas discharge are such that dilution and contamination of the intake air will not prevent operation of the EDG at rated power output or cause engine shutdown as a consequence of any metrological or accident condition. Each EDG set has a separate, independent diesel engine combustion air and exhaust gas system, as shown in Figure 9.5.8-1—Emergency Diesel Generator Air Intake and Exhaust System. ● The safety-related portions of the DGAIES are designed in accordance with Seismic Category I. Safety-related systems are required to function following a DBA, and are required to achieve and maintain a safe shutdown condition. ● Safety functions can be performed, assuming a single active component failure coincident with the LOOP (GDC 17). ● None of the safety-related components of the DGAIES are shared with any other division or unit (GDC 5). -

Mopar Perf Parts Catalog.Pdf
AT MOPAR ®, WE TURN CARS INTO SOMETHING MORE. INTO SOMETHING YOU PASS ON. INTO MYTH. INTO A LEGEND. EVERY PART IS PART OF A LEGACY. AND THAT LEGACY IS YOURS. DODGE CHALLENGER DODGE VIPER 8 Air Induction Systems 38 Brakes 06 9 Exhaust Systems 36 39 Suspension and Steering 10 Suspension Upgrades and Components 39 Wheels 12 Shaker Hoods and Kits 12 T/A Performance Hoods and Components 14 Wheels CHRYSLER 300 42 Air Induction Systems 15 Brakes 40 42 Exhaust Systems 16 Stage Packages 43 Filter 17 Bee-Liever Packages 44 Suspension Upgrades and Components 17 Powertrain Control Modules 46 Stage Performance Packages 17 Filter 47 Brakes DODGE CHARGER 47 Powertrain Control Modules 20 Air Induction Systems RAM 1500 18 20 Exhaust Systems 50 Air Induction Systems 21 Brakes 48 51 Exhaust Systems 21 Wheels 52 Suspension Upgrades and Components 22 Suspension Upgrades and Components 54 Leveling Kits 24 Stage Packages 55 Wheels 25 Bee-Liever Packages 25 Powertrain Control Modules 25 Filter RAM 2500/3500 58 Winch & Mounting Components 56 58 Leveling Kits DODGE DURANGO 59 Lift Kits 28 Air Induction 59 Steering 26 29 Exhaust Systems 29 Suspension Upgrades PERFORMANCE DODGE DART 60GAUGES & LIGHTS 32 Air Induction Systems 62 Gauges 30 32 Exhaust Systems 65 Gauge Pods 33 Performance Hood and Venting 66 SilverStar Lighting 34 Aerodynamics 35 Brakes 35 Suspension Upgrades LIMITED 35 Wheels *Many images shown throughout the catalog are representative 68WARRANTIES of the product. Actual product may vary. WHY US? THAT’S A GOOD QUESTION. For starters, we were there when your car was just a sparkle in a designer’s eye. -

One-Dimensional Gas Flow Analysis of the Intake and Exhaust System of a Single Cylinder Diesel Engine
Journal of Marine Science and Engineering Article One-Dimensional Gas Flow Analysis of the Intake and Exhaust System of a Single Cylinder Diesel Engine Kyong-Hyon Kim 1 and Kyeong-Ju Kong 2,* 1 Training Ship Management Center, Pukyong National University, Busan 48513, Korea; bluefi[email protected] 2 Department of Mechanical System Engineering, Graduate School, Pukyong National University, Busan 48513, Korea * Correspondence: [email protected]; Tel.: +82-51-629-6188 Received: 1 December 2020; Accepted: 18 December 2020; Published: 20 December 2020 Abstract: In order to design a diesel engine system and to predict its performance, it is necessary to analyze the gas flow of the intake and exhaust system. Gas flow analysis in a three-dimensional (3D) format needs a high-resolution workstation and an enormous amount of time for analysis. Calculation using the method of characteristics (MOC), which is a gas flow analysis in a one-dimensional (1D) format, has a fast calculation time and can be analyzed with a low-resolution workstation. However, there is a problem with poor accuracy in certain areas. It was assumed that the reason was that 1D could not implement the shape. The error that occurs in the shape of the bent pipe used in the intake and exhaust ports of the diesel engine was analyzed and to find a solution to the low accuracy, the results of the experiment and 1D analysis were compared. The discharge coefficient was calculated using the average mass flow rate, and as a result of applying it, the accuracy was improved for the maximum negative pressure by 0.56–1.93% and the maximum pressure by 3.11–7.86% among the intake pipe pressure results. -

ENGINE Internally Lubricated Parts Including
Inside5pgFldout 12/14/05 09:43 AM Page 1 ENGINE Internally • Cylinder Heads • Water Pump • Extension Housing • Sprags • Cooling fan clutch DIFFERENTIAL – FUEL – • Center Link lubricated parts • Intake Manifold • Water Pump Pulley Gasket • Springs • Cooling fan electric (Primary Drive) – • Fuel tank and lines • Control Rings including: • Intake Valves • Gears • Sprockets motors • Pinion Bearings • Fuel Sending Unit • Control Valve • Pistons • Intercooler The engine block and • Governor • Stator • Pinion Gear • Fuel Inject Metering • Cups • Piston Rings • Lifters cylinder heads are also • Governor Cover • Stator Shaft SEALS AND GASKETS – • Pinion Flange Pump • Drag Link • Piston Pins • Main Bearing Caps covered if caused by a • Governor Gear • Sun Gear Shell • Head gasket(s) • Propeller Shafts; • Fuel Injectors • Pitman Arm failure of any of the • Crankshaft and Main • Main Bearings • Idler Shaft • Sun Gears • Intake Manifold “U” joints • Fuel Distributor • Pitman Shaft Bearings above covered items. • Oil Cooler • Input Shaft • Synchronizer Hub Gasket • Axle Shafts • Fuel pump housing • Pitman Shaft Adjuster • Camshaft and • Oil Cooler Lines • Inspection Plugs • Synchronizer Key(s) • Upper Plenum Gasket • Axle Bearings & • Diaphragms • Pitman Shaft Seal Bearings TRANSMISSION – Races • Oil Filter Adapter • Intermediate Shaft • Synchronizer Ring • Valve Cover Gasket • Springs O-ring • Timing Chain Automatic or Manual: • Axle Flange • Oil Pan • Main Shaft • Synchronizer Sleeves • Water Pump Gasket • Valves and Actuating • Pump Shaft • Timing -

Development of Electric Supercharger to Facilitate the Downsizing of Automobile Engines
Mitsubishi Heavy Industries Technical Review Vol. 47 No. 4 (December 2010) 7 Development of Electric Supercharger to Facilitate the Downsizing of Automobile Engines YUKIO YAMASHITA*1 SEIICHI IBARAKI*2 KUNIO SUMIDA*1 MOTOKI EBISU*3 BYEONGIL AN*4 HIROSHI OGITA*5 To satisfy both environmental regulations and drivability requirements, high-level control of automobile engines is currently in demand, and electrification is in progress. An electric supercharger, in which a supercharging compressor is driven by a high-speed motor instead of an exhaust turbine or belt, eliminates turbo lag by making use of the motor’s high-speed response. An engine with an electric supercharger offers comparable fuel consumption to a naturally aspirated engine, and is expected to facilitate the downsizing of engines. In this paper, we introduce the electric supercharger developed by Mitsubishi Heavy Industries, Ltd. (MHI), including bench test results exhibiting a high-speed response of 1.0-s acceleration time to attain a compressor operating point rated at 2 kW, 140,000 rpm. |1. Introduction With the ongoing movement toward global environmental protection, regulations controlling the exhaust emissions and fuel consumption of automobiles are being enforced. Turbochargers have improved the performance of diesel engines; currently, almost all diesel vehicles are equipped with turbochargers. More and more gasoline engines are also being fitted with turbochargers to decrease weight and increase efficiency1. In recent years, engine controls have become widely diversified for the sake of both the environment and operating performance. Variable geometry (VG) turbochargers, which can vary the turbine capacity in response to the engine load, are becoming increasingly popular. -

Setting Valve Lash on an Inline 6
SETTING VALVE LASH ON AN INLINE 6 STEP 1: Remove all valve covers from the engine. STEP 2: Rotate the crankshaft until the engine is at TDC #1. Use the markings on the flywheel to determine when the engine is at TDC. Check the rocker arms on cylinder #1, which is the cylinder closest to the flywheel. If the rocker arms are slightly loose and can be moved around a little, the camshaft is in the correct spot to begin checking and setting valve lash. If the rocker arms feel tight, rotate the crankshaft 360 degrees until it is at TDC #1 again, then check the rockers on cylinder #1 – they should now move slightly. Another way to verify that the camshaft is in the correct position is to watch the rockers on cylinder #1 as the crankshaft is rotated. If the rockers are moving as the crankshaft approaches TDC #1, the crank will need to be rotated 360 degrees to set the engine for timing. If the rockers on cylinder #1 do not move as you approach TDC #1, the timing is correct and you may begin checking valve lash. Start with the valves indicated on the picture below with a WHITE ARROW. STEP 3: Use a 17mm wrench to loosen the nut around the lash adjuster you are going to set. Use a screwdriver to set the valve lash adjuster so that the feeler gauge of your desired thickness fits into the gap between the rocker arm and the valve tip. The gauge should fit snugly, but should still slide in and out – don’t clamp the rocker arm onto the feeler gauge. -

Intercooler Information Sheet English
Intercooler EXPERIENCE THE DIFFERENCE: Heat exchanger boosting Range & Availability Mechanical and Thermal Stress Resistance air-charged engines Competitive range of intercoolers covering the most popular car, van and truck models. Plastic tanks designed with special Program of more than 520 items covering reinforcing inner crossbars and specially 1,700 OE numbers and more than 88% of the strengthened inlets and outlets, to European car park. Role & Operation protect the tank against stress caused by high temperatures and mechanical Thermal Stress Efficient, Reliable & Safe tensions. Resistance The intercooler significantly improves the Reinforced with at least 30-35% combustion process in turbo-charged systems, Designed and manufactured towards the Specially designed side panels with aftermarket, while thoroughly tested to match fiberglass. No recycled plastics are thus increasing the engine power effect. cuts to lower the influence of thermal OE quality - Nissens intercoolers are submitted used in the mixture. All Nissens’ expansion on the core construction. to corrosion, vibration, pressure impulse, thermal truck intercoolers are custom-welded, The main role of the intercooler is to reduce the expansion and thermal performance tests. ensuring an exceptionally strong and temperature of the hot air compressed by the durable welding seam. turbocharger, before it reaches the engine’s Easy-handling packaging and excellent protection against transport damages. combustion chamber. This has a significant impact Optimized on the charge effect, as the cooled air has a much Supreme thermal performance and extended Design higher density in terms of air molecules per cubic lifespan thanks to a number of special features Specially designed core centimeter. This increases the volume of intake air, applied to Nissens intercoolers. -

Intake Valve and Combustion Chamber Deposits Formation – the Engine and Fuel Related Factors That Impacts Their Growth
NAFTA-GAZ, ROK LXX, Nr 4 / 2014 Zbigniew Stępień Instytut Nafty i Gazu – Państwowy Instytut Badawczy Intake valve and combustion chamber deposits formation – the engine and fuel related factors that impacts their growth Deposit forming tendency on the internal surfaces of spark ignition engines parts including IVD (Intake Valve De- posits) and CCD (Combustion Chamber Deposits) is one relevant parameter which causes driveability problems, affects engine durability and is of increasing concern in the automobile industry. The paper summarizes knowledge concerning the impact of engine operating conditions and fuel composition on the formation of IVD and CCD. On the basis of literature reviews and one’s own research results, some interesting issues involved in the engine deposit accumulation and factors that influence their growth has been discussed. Until now at the Oil and Gas Institute (INiG) about 380 engine tests in compliance with CEC F-05-93 procedure, and about 220 in accordance with CEC F-20-98 procedure have been performed. This paper also covers description of the effects of deposits build-up on engine performance and its operational properties. Key words: Piston Internal Combustion Engines, Intake Valve Deposits, Combustion Chambers Deposits. Tworzenie osadów na zaworach dolotowych i w komorach spalania silników – czynniki wpływające na wzrost osadów związane z silnikiem i paliwem Skłonność do tworzenia osadów na powierzchniach wewnętrznych części silników z zapłonem iskrowym, w tym osadów na zaworach dolotowych (IVD) i w komorach spalania (CCD), jest jednym z najistotniejszych czynników pogarszających właściwości użytkowo-eksploatacyjne pojazdu, oddziałujących na trwałość silnika i wywołujących zaniepokojenie w przemyśle motoryzacyjnym. Artykuł podsumowuje, w skrócie, wiedzę dotyczącą wpływu warun- ków eksploatacji silnika i składu paliwa na tworzenie IVD i CCD.