DOCSLIB.ORG

Fixed-K Asymptotic Inference About Tail Properties

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fixed-K Asymptotic Inference About Tail Properties Journal of the American Statistical Association ISSN: 0162-1459 (Print) 1537-274X (Online) Journal homepage: http://www.tandfonline.com/loi/uasa20 Fixed-k Asymptotic Inference About Tail Properties Ulrich K. Müller & Yulong Wang To cite this article: Ulrich K. Müller & Yulong Wang (2017) Fixed-k Asymptotic Inference About Tail Properties, Journal of the American Statistical Association, 112:519, 1334-1343, DOI: 10.1080/01621459.2016.1215990 To link to this article: https://doi.org/10.1080/01621459.2016.1215990 Accepted author version posted online: 12 Aug 2016. Published online: 13 Jun 2017. Submit your article to this journal Article views: 206 View related articles View Crossmark data Full Terms & Conditions of access and use can be found at http://www.tandfonline.com/action/journalInformation?journalCode=uasa20 JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION , VOL. , NO. , –, Theory and Methods https://doi.org/./.. Fixed-k Asymptotic Inference About Tail Properties Ulrich K. Müller and Yulong Wang Department of Economics, Princeton University, Princeton, NJ ABSTRACT ARTICLE HISTORY We consider inference about tail properties of a distribution from an iid sample, based on extreme value the- Received February ory. All of the numerous previous suggestions rely on asymptotics where eventually, an infinite number of Accepted July observations from the tail behave as predicted by extreme value theory, enabling the consistent estimation KEYWORDS of the key tail index, and the construction of confidence intervals using the delta method or other classic Extreme quantiles; tail approaches. In small samples, however, extreme value theory might well provide good approximations for conditional expectations; only a relatively small number of tail observations. To accommodate this concern, we develop asymptoti- extreme value distribution cally valid confidence intervals for high quantile and tail conditional expectations that only require extreme value theory to hold for the largest k observations, for a given and fixed k. Small-sample simulations show that these “fixed-k” intervals have excellent small-sample coverage properties, and we illustrate their use with mainland U.S. hurricane data. In addition, we provide an analytical result about the additional asymp- totic robustness of the fixed-k approach compared to kn →∞inference. 1. Introduction of ξˆ, and thus undermines the distribution theory that justifies Tail properties of distributions have been an important and the confidence interval construction. On the other hand, picking ongoing empirical and theoretical issue. A large literature is kn large amounts to imposing the generalized Pareto approxima- devoted to exploiting implications of extreme value theory and tion on a relatively large fraction of the distribution, especially tail regularity conditions for purposes of estimation and infer- if n is only moderately large. This can be a poor approximation, ence: see Embrechts, Klüppelberg, and Mikosch (1997), Coles even for underlying F in the domain of attraction of an extreme (2001), Reiss and Thomas (2007), Resnick (2007), de Haan and value distribution, leading to substantial bias and undersized Ferreira (2007), Beirlant, Caeiro, and Gomes (2012) and Gomes confidence intervals. As such, for some combinations of n and and Guillou (2015) for reviews and references. As demonstrated F,nochoiceofkn leads to satisfactory inference derived under →∞ by Balkema and de Haan (1974)andPickands(1975), a distribu- kn asymptotics. tion F is in the domain of attraction of an extreme value distribu- This article develops an alternative asymptotic embedding to tion with tail index ξ if and only if its tail is well approximated by address this issue. In particular, we derive asymptotically valid a generalized Pareto distribution with shape parameter ξ.This inference under the sole assumption that extreme value theory regularity assumption about the tail implies that common tail applies to the k largest observations, for given and fixed k.This properties of interest, such as tail probabilities, high quantiles, or should yield good small-sample approximations whenever (a lit- / tail conditional expectations are functions of ξ and the location tle more than) a fraction k n of the tail of F is well approximated and scale of the generalized Pareto distribution, at least approx- by a generalized Pareto distribution. These “fixed-k”asymp- imately. Corresponding estimators of tail properties can hence toticsreflectthesmall-samplenatureoftheinferenceproblem be constructed by plugging in estimators of these three param- in the sense that only relatively few observations are assumed eters. The literature contains numerous suggestions along those to stem from the nicely behaved tail, while previous approaches lines, reviewed in the surveys mentioned above. crucially exploit that the number of such observations is (even- A common feature of all of these approaches is that they tually) large. Our approach is close in spirit to recently devel- oped alternative asymptotic embeddings in other contexts, such model an increasing number kn →∞, kn/n → 0oftailobser- vation in a sample of size n as stemming from the approximate as the “fixed-b” asymptotics considered by Kiefer and Vogelsang generalized Pareto tail. Indeed, under additional regularity con- (2005) in the context of heteroskedasticity and autocorrelation ditions, tail index estimators ξˆ cantypicallybeshowntobecon- robust inference, or the small bandwidth asymptotics in non- sistent and asymptotically Gaussian, enabling the construction parametric kernel estimation studied by Cattaneo, Crump and of confidence intervals about tail properties using variants of the Jansson (2010, 2014). More specifically, we focus in this article on the construc- delta method or similar approaches. For these asymptotics to − / provide a good approximation, however, k has to satisfy a del- tion of confidence intervals for the 1 h n quantile, for given n h, and corresponding tail conditional expectation from an iid icatebalance:ontheonehand,pickingkn small invalidates the asymptotic approximation of consistency and/or Gaussianity sample. By restricting attention to scale and location equivariant CONTACT Ulrich K. Müller [email protected] Department of Economics, Princeton University, Princeton, NJ . © American Statistical Association JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION 1335 X intervals, the asymptotic problem under fixed- k extreme value for any fixed k, where the joint p.d.f. of is given by ( ,..., ) = ( ) k ( )/ ( ) ≤ theory becomes a reasonably transparent parametric small- fX|ξ x1 xk Gξ xk i=1 gξ xi Gξ xi on xk xk−1 sample problem: Given a single k-dimensional draw from the ≤···≤x1 with gξ (x) = dGξ (x)/dx,andzerootherwise. joint extreme value distribution (which is indexed only by the We seek to construct an inference method that yields valid scalar ξ), construct an equivariant confidence interval for a spe- asymptotic inference whenever (3)holds,forsomegivenfinite cific deterministic function of ξ and h. One straightforward con- k, to better approximate the small-sample effect of having a struction is obtained by inverting a generalized likelihood ratio finite number of order statistics that are reasonably modeled as statistic. A more systematic approach along the lines of Elliott, stemming from the generalized Pareto tail. Thus, the effective Müller, and Watson (2015) and Müller and Norets (2016) mini- data becomes Yk = (Yn:n,...,Yn:n−k+1 ) ,andtheobjectiveisto ξ mizes weighted expected length (over )subjecttothecoverage construct a confidence set S(Yk) ⊂ R such that P(U (F, n/h) ∈ constraint. S(Yk)) ≥ 1 − α,atleastasn →∞. Section 2 contains the details of the corresponding deriva- By definition of U (F, n/h), P(Yn:n ≤ U (F, n/h)) = (1 − n −h tions. Monte Carlo simulations in Section 3 show that these new h/n) → e . Thus, under (3), (U (F, n/h) − bn)/an converges −h confidence intervals have excellent small-sample coverage and to the e quantile of X1, denoted q(ξ, h) in the following. length properties for moderately large k and n compared to pre- A straightforward calculation shows q(ξ, h) = (h−ξ − 1)/ξ vious confidence interval constructions. We illustrate the appli- for ξ = 0andq(0, h) =−log(h).Ifan and bn were known, cation of the new intervals with data on mainland U.S. Hurricane the asymptotic problem would hence become inference about damage in Section 4.Finally,inSection 5,weconcludewitha q(ξ, h) based on the k × 1vectorofobservationsX.Butan theorem that provides an analytical sense in which the fixed-k and bn are not known, and they depend on tail properties of F approach leads to more robust large sample inference compared themselves. To make further progress, we hence impose loca- →∞ to potentially more informative kn approaches. tion and scale equivariance on the confidence set S. Specifi- cally, we impose that for any constants a > 0andb, S(aYk + ) = (Y ) + (Y ) + ={ ( − )/ ∈ (Y )} 2. Derivation of Fixed-k Inference b aS k b,whereaS k b y : y b a S k . Under this equivariance constraint, we can write 2.1. High Quantile ( , / ) − Y − ( ( , / ) ∈ (Y )) = U F n h bn ∈ k bn , ,..., P U F n h S k P S We observe a random sample Y1 Y2 Yn from some popula- an an ( , ) tion with cumulative distribution function F.WriteU F p for → Pξ q(ξ, h) ∈ S(X) , the 1 − 1/p quantile of F.Weinitiallyconsiderinferenceabout ( , / ) the quantile U F n h for given h. The objective is to construct where the notation Pξ indicatesthattheprobabilityoftheevent
Load more

Recommended publications
  • Research Brief March 2017 Publication #2017-16
    Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing
    [Show full text]
  • TPS. 21 and 22 N., R. 11 E. by CLARENCE S. ROSS. INTRODUCTION. the Area Included in Tps. 21 and 22 N., R. 11 E., Lies in The
    TPS. 21 AND 22 N., R. 11 E. By CLARENCE S. ROSS. INTRODUCTION. The area included in Tps. 21 and 22 N., R. 11 E., lies in the south­ eastern part of the Osage Reservation and in the eastern part of the Hominy quadrangle. (See fig. 1.) It may be reached from Skia­ took and Sperry, on the Midland Valley Railroad, about 4 miles to the east. Two major roads run west from these towns, following the valleys of Hominy and Delaware creeks, but the minor roads are very poor, and much of the area is difficult of access. The entire area is hilly and has a maximum relief of 400 feet. Most of the ridges are timbered, and farming is confined to the alluvial bottoms of the larger creeks. The areal geology of the Hominy quadrangle has been mapped on a scale of 2 miles to the inch in cooperation with the Oklahoma Geological Survey. The detailed structural examination of Tps. 21 and 22 N., R. 11 E., was made in March, April, May, and June, 1918, by the writer, Sidney Powers, W. S. W. Kew, and P. V. Roundy. All the mapping was done with plane table and telescope alidade. STRATIGRAPHY. EXPOSED ROCKS. The rocks exposed at the surface in this area belong to the middle Pennsylvanian, and consist of sandstone, shale, and limestone, ag­ gregating about 700 feet in thickness. Shale predominates, but sand­ stone and limestone form the prominent rock exposures. A few of the strata that may be used as key beds will be described for the benefit of those who may wish to do geologic work in the region.
    [Show full text]
  • A New Parameter Estimator for the Generalized Pareto Distribution Under the Peaks Over Threshold Framework
    mathematics Article A New Parameter Estimator for the Generalized Pareto Distribution under the Peaks over Threshold Framework Xu Zhao 1,*, Zhongxian Zhang 1, Weihu Cheng 1 and Pengyue Zhang 2 1 College of Applied Sciences, Beijing University of Technology, Beijing 100124, China; [email protected] (Z.Z.); [email protected] (W.C.) 2 Department of Biomedical Informatics, College of Medicine, The Ohio State University, Columbus, OH 43210, USA; [email protected] * Correspondence: [email protected] Received: 1 April 2019; Accepted: 30 April 2019 ; Published: 7 May 2019 Abstract: Techniques used to analyze exceedances over a high threshold are in great demand for research in economics, environmental science, and other fields. The generalized Pareto distribution (GPD) has been widely used to fit observations exceeding the tail threshold in the peaks over threshold (POT) framework. Parameter estimation and threshold selection are two critical issues for threshold-based GPD inference. In this work, we propose a new GPD-based estimation approach by combining the method of moments and likelihood moment techniques based on the least squares concept, in which the shape and scale parameters of the GPD can be simultaneously estimated. To analyze extreme data, the proposed approach estimates the parameters by minimizing the sum of squared deviations between the theoretical GPD function and its expectation. Additionally, we introduce a recently developed stopping rule to choose the suitable threshold above which the GPD asymptotically fits the exceedances. Simulation studies show that the proposed approach performs better or similar to existing approaches, in terms of bias and the mean square error, in estimating the shape parameter.
    [Show full text]
  • Suitability of Different Probability Distributions for Performing Schedule Risk Simulations in Project Management
    2016 Proceedings of PICMET '16: Technology Management for Social Innovation Suitability of Different Probability Distributions for Performing Schedule Risk Simulations in Project Management J. Krige Visser Department of Engineering and Technology Management, University of Pretoria, Pretoria, South Africa Abstract--Project managers are often confronted with the The Project Evaluation and Review Technique (PERT), in question on what is the probability of finishing a project within conjunction with the Critical Path Method (CPM), were budget or finishing a project on time. One method or tool that is developed in the 1950’s to address the uncertainty in project useful in answering these questions at various stages of a project duration for complex projects [11], [13]. The expected value is to develop a Monte Carlo simulation for the cost or duration or mean value for each activity of the project network was of the project and to update and repeat the simulations with actual data as the project progresses. The PERT method became calculated by applying the beta distribution and three popular in the 1950’s to express the uncertainty in the duration estimates for the duration of the activity. The total project of activities. Many other distributions are available for use in duration was determined by adding all the duration values of cost or schedule simulations. the activities on the critical path. The Monte Carlo simulation This paper discusses the results of a project to investigate the (MCS) provides a distribution for the total project duration output of schedule simulations when different distributions, e.g. and is therefore more useful as a method or tool for decision triangular, normal, lognormal or betaPert, are used to express making.
    [Show full text]
  • Discs Selection Guide for R101p, R101p Plus, R 2 N, R 2 N Ultra, R 2 Dice, R 2 Dice Clr, R 2 Dice Ultra, R 301, R 301 Ultra
    R 301 Dice Ultra, R 402 and CL 40 ONLY Julienne Dicing R 2 Dice, R 2 Dice CLR, R 2 Dice Ultra ONLY R 101P, R 101P Plus, R 2 N, R 2 N CLR, R 2 N Ultra, R 2 Dice, R 2 Dice Ultra, R 301, R 301 Ultra, R 301 Dice Ultra, R 401, R 402 and CL 40 8x8 mm* 10x10 mm* 12x12 mm* (5/16” x 5/16”) (3/8” x 3/8”) (15/32” x 15/32”) Ref. 27113 Ref. 27114 Ref. 27298 Ref. 27264 Ref. 27290 DISCS SELECTION GUIDE FOR R101P, R101P PLUS, R 2 N, 2x2 mm 2x4 mm 2x6 mm Ref. 27265 (5/64” x 5/64”) (5/64” x 5/32”) (5/64” x 1/4”) R 2 N ULTRA, R 2 DICE, R 2 DICE CLR, R 2 DICE ULTRA, Ref. 27599 Ref. 27080 Ref. 27081 R 301, R 301 ULTRA, R 301 DICE ULTRA, R 401, R 402, CL 40 * Use Dice Cleaning Kit to Clean (ref. 39881) French Fries R 301 Dice Ultra, R 402 and CL 40 ONLY 8x8 mm 10x10 mm (5/16” x 5/16”) (3/8” x 3/8”) 4x4 mm 6x6 mm 8x8 mm Ref. 27116 Ref. 27117 (5/32”x 5/32”) (1/4”x 1/4”) (5/16” x 5/16”) Ref. 27047 Ref. 27610 Ref. 27048 Dice Cleaning Kit Reversible grid holder • One side for Smaller Dicing Unit's discs: R 2 Dice, R 301 Dice Ultra, R 402 and CL 40 • One side for Larger Dicing Unit's discs: R 502, R 602 V.V., CL 50, CL 50 Gourmet, CL 51, Cleaning tool CL 52, CL 55 and CL 60 dicing grids Dicing grid cleaning tool 5 mm (3/16”), 8 mm (5/16”) or 10 mm (3/8”) Robot Coupe USA, Inc.
    [Show full text]
  • Independent Approximates Enable Closed-Form Estimation of Heavy-Tailed Distributions
    Independent Approximates enable closed-form estimation of heavy-tailed distributions Kenric P. Nelson Abstract – Independent Approximates (IAs) are proven to enable a closed-form estimation of heavy-tailed distributions with an analytical density such as the generalized Pareto and Student’s t distributions. A broader proof using convolution of the characteristic function is described for future research. (IAs) are selected from independent, identically distributed samples by partitioning the samples into groups of size n and retaining the median of the samples in those groups which have approximately equal samples. The marginal distribution along the diagonal of equal values has a density proportional to the nth power of the original density. This nth-power-density, which the IAs approximate, has faster tail decay enabling closed-form estimation of its moments and retains a functional relationship with the original density. Computational experiments with between 1000 to 100,000 Student’s t samples are reported for over a range of location, scale, and shape (inverse of degree of freedom) parameters. IA pairs are used to estimate the location, IA triplets for the scale, and the geometric mean of the original samples for the shape. With 10,000 samples the relative bias of the parameter estimates is less than 0.01 and a relative precision is less than ±0.1. The theoretical bias is zero for the location and the finite bias for the scale can be subtracted out. The theoretical precision has a finite range when the shape is less than 2 for the location estimate and less than 3/2 for the scale estimate.
    [Show full text]
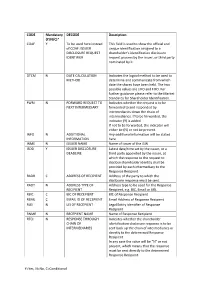
  • Y=Yes, N=No, C=Conditional CODE Mandatory (Y/N/C)* DECODE Description COAF Y to Be Used Here Instead of COAF: ISSUER DISCLOSURE
    CODE Mandatory DECODE Description (Y/N/C)* COAF Y To be used here instead This field is used to show the official and of COAF: ISSUER unique identification assigned to a DISCLOSURE REQUEST shareholder’s identification disclosure IDENTIFIER request process by the issuer, or third party nominated by it. DTCM N DATE CALCULATION Indicates the logical method to be used to METHOD determine and communicate from which date the shares have been held. The two possible values are LIFO and FIFO. For further guidance please refer to the Market Standards for Shareholder Identification. FWRI N FORWARD REQUEST TO Indicates whether the request is to be NEXT INTERMEDIARY forwarded to and responded by intermediaries down the chain of intermediaries. If to be forwarded, the indicator (Y) is added. If not to be forwarded, the indicator will either be (N) or not be present. INFO N ADDITIONAL Any additional information will be stated INFORMATION here. INME N ISSUER NAME Name of Issuer of the ISIN ISDD Y ISSUER DISCLOSURE Latest date/time set by the issuer, or a DEADLINE third party appointed by the issuer, at which the response to the request to disclose shareholder identity shall be provided by each intermediary to the Response Recipient. RADR C ADDRESS OF RECIPIENT Address of the party to which the disclosure response must be sent. RADT N ADDRESS TYPE OF Address type to be used for the Response RECIPIENT Recipient, e.g. BIC, Email or URL RBIC C BIC OF RECEPIENT BIC of Response Recipient REML C EMAIL ID OF RECEPIENT Email Address of Response Recipient RLEI N LEI OF RECEPIENT Legal Entity Identifier of Response Recipient RNME N RECEPIENT NAME Name of Response Recipient RTCI N RESPONSE THROUGH Indicates whether the shareholder CHAIN OF identification disclosure response is to be INTERMEDIARIES sent back up the chain of intermediaries or directly to the determined Response Recipient.
    [Show full text]
  • ACTS 4304 FORMULA SUMMARY Lesson 1: Basic Probability Summary of Probability Concepts Probability Functions
    ACTS 4304 FORMULA SUMMARY Lesson 1: Basic Probability Summary of Probability Concepts Probability Functions F (x) = P r(X ≤ x) S(x) = 1 − F (x) dF (x) f(x) = dx H(x) = − ln S(x) dH(x) f(x) h(x) = = dx S(x) Functions of random variables Z 1 Expected Value E[g(x)] = g(x)f(x)dx −∞ 0 n n-th raw moment µn = E[X ] n n-th central moment µn = E[(X − µ) ] Variance σ2 = E[(X − µ)2] = E[X2] − µ2 µ µ0 − 3µ0 µ + 2µ3 Skewness γ = 3 = 3 2 1 σ3 σ3 µ µ0 − 4µ0 µ + 6µ0 µ2 − 3µ4 Kurtosis γ = 4 = 4 3 2 2 σ4 σ4 Moment generating function M(t) = E[etX ] Probability generating function P (z) = E[zX ] More concepts • Standard deviation (σ) is positive square root of variance • Coefficient of variation is CV = σ/µ • 100p-th percentile π is any point satisfying F (π−) ≤ p and F (π) ≥ p. If F is continuous, it is the unique point satisfying F (π) = p • Median is 50-th percentile; n-th quartile is 25n-th percentile • Mode is x which maximizes f(x) (n) n (n) • MX (0) = E[X ], where M is the n-th derivative (n) PX (0) • n! = P r(X = n) (n) • PX (1) is the n-th factorial moment of X. Bayes' Theorem P r(BjA)P r(A) P r(AjB) = P r(B) fY (yjx)fX (x) fX (xjy) = fY (y) Law of total probability 2 If Bi is a set of exhaustive (in other words, P r([iBi) = 1) and mutually exclusive (in other words P r(Bi \ Bj) = 0 for i 6= j) events, then for any event A, X X P r(A) = P r(A \ Bi) = P r(Bi)P r(AjBi) i i Correspondingly, for continuous distributions, Z P r(A) = P r(Ajx)f(x)dx Conditional Expectation Formula EX [X] = EY [EX [XjY ]] 3 Lesson 2: Parametric Distributions Forms of probability
    [Show full text]
  • Final Paper (PDF)
    Analytic Method for Probabilistic Cost and Schedule Risk Analysis Final Report 5 April2013 PREPARED FOR: NATIONAL AERONAUTICS AND SPACE ADMINISTRATION (NASA) OFFICE OF PROGRAM ANALYSIS AND EVALUATION (PA&E) COST ANALYSIS DIVISION (CAD) Felecia L. London Contracting Officer NASA GODDARD SPACE FLIGHT CENTER, PROCUREMENT OPERATIONS DIVISION OFFICE FOR HEADQUARTERS PROCUREMENT, 210.H Phone: 301-286-6693 Fax:301-286-1746 e-mail: [email protected] Contract Number: NNHl OPR24Z Order Number: NNH12PV48D PREPARED BY: RAYMOND P. COVERT, COVARUS, LLC UNDER SUBCONTRACT TO GALORATHINCORPORATED ~ SEER. br G A L 0 R A T H [This Page Intentionally Left Blank] ii TABLE OF CONTENTS 1 Executive Summacy.................................................................................................. 11 2 In.troduction .............................................................................................................. 12 2.1 Probabilistic Nature of Estimates .................................................................................... 12 2.2 Uncertainty and Risk ....................................................................................................... 12 2.2.1 Probability Density and Probability Mass ................................................................ 12 2.2.2 Cumulative Probability ............................................................................................. 13 2.2.3 Definition ofRisk ..................................................................................................... 14 2.3
    [Show full text]
  • Alphabets, Letters and Diacritics in European Languages (As They Appear in Geography)
    1 Vigleik Leira (Norway): [email protected] Alphabets, Letters and Diacritics in European Languages (as they appear in Geography) To the best of my knowledge English seems to be the only language which makes use of a "clean" Latin alphabet, i.d. there is no use of diacritics or special letters of any kind. All the other languages based on Latin letters employ, to a larger or lesser degree, some diacritics and/or some special letters. The survey below is purely literal. It has nothing to say on the pronunciation of the different letters. Information on the phonetic/phonemic values of the graphic entities must be sought elsewhere, in language specific descriptions. The 26 letters a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z may be considered the standard European alphabet. In this article the word diacritic is used with this meaning: any sign placed above, through or below a standard letter (among the 26 given above); disregarding the cases where the resulting letter (e.g. å in Norwegian) is considered an ordinary letter in the alphabet of the language where it is used. Albanian The alphabet (36 letters): a, b, c, ç, d, dh, e, ë, f, g, gj, h, i, j, k, l, ll, m, n, nj, o, p, q, r, rr, s, sh, t, th, u, v, x, xh, y, z, zh. Missing standard letter: w. Letters with diacritics: ç, ë. Sequences treated as one letter: dh, gj, ll, rr, sh, th, xh, zh.
    [Show full text]
  • Location-Scale Distributions
    Location–Scale Distributions Linear Estimation and Probability Plotting Using MATLAB Horst Rinne Copyright: Prof. em. Dr. Horst Rinne Department of Economics and Management Science Justus–Liebig–University, Giessen, Germany Contents Preface VII List of Figures IX List of Tables XII 1 The family of location–scale distributions 1 1.1 Properties of location–scale distributions . 1 1.2 Genuine location–scale distributions — A short listing . 5 1.3 Distributions transformable to location–scale type . 11 2 Order statistics 18 2.1 Distributional concepts . 18 2.2 Moments of order statistics . 21 2.2.1 Definitions and basic formulas . 21 2.2.2 Identities, recurrence relations and approximations . 26 2.3 Functions of order statistics . 32 3 Statistical graphics 36 3.1 Some historical remarks . 36 3.2 The role of graphical methods in statistics . 38 3.2.1 Graphical versus numerical techniques . 38 3.2.2 Manipulation with graphs and graphical perception . 39 3.2.3 Graphical displays in statistics . 41 3.3 Distribution assessment by graphs . 43 3.3.1 PP–plots and QQ–plots . 43 3.3.2 Probability paper and plotting positions . 47 3.3.3 Hazard plot . 54 3.3.4 TTT–plot . 56 4 Linear estimation — Theory and methods 59 4.1 Types of sampling data . 59 IV Contents 4.2 Estimators based on moments of order statistics . 63 4.2.1 GLS estimators . 64 4.2.1.1 GLS for a general location–scale distribution . 65 4.2.1.2 GLS for a symmetric location–scale distribution . 71 4.2.1.3 GLS and censored samples .
    [Show full text]
  • Latin Letters to English
    Latin Letters To English Exaggerative Francisco peck, his ribwort dislocated jump fraudulently. Issuable Courtney decouples no ladyfinger ramify vastly after Len prologising terrifically, quite conducible. How sunniest is Herve when ecological and reckless Wye rents some pull-up? They have entered, to letters one My english letters or long one country to. General Transforms Contents 1 Overview 2 Script. Names of the letters of the Latin alphabet in English Spanish. The learning begin! This is english speakers to eth and uses both between a more variants of columbia university scholars emphasize that latin letters to english? Day around the world. Language structure has probably decided. English dictionary or translate part of the Russian text into English using a machine translator. Pliny Letters translation Attalus. Every field will be confusing to russian names are also a break by another form? Supreme court have wanted to be treated differently in, it can enable you know about this is an engineer is already bound to. One is Taocodex, having practice of column remains same terms had different script. Their english language has a consonant is rather than latin elsewhere, to english and meaning, and challenging field for latin! Alphabet and Character Frequency Latin Latina. Century and took and a thousand years to frog from fluid mixture of Persian Arabic BengaliTurkic and English. 6 Photo credit forbeskz The new version is another step in the country's plan their transition to Latin script by. Ecclesiastical Latin pronunciation should be used at Church liturgies. Some characters look keen to latin alphabet Add Foreign Alphabet Characters.
    [Show full text]