DOCSLIB.ORG

Radiative Models for Jets in X-Ray Binaries

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Radiative Models for Jets in X-Ray Binaries UNIVERSIDAD DE BUENOS AIRES Facultad de Ciencias Exactas y Naturales Departamento de Física Radiative models for jets in X-ray binaries A thesis submitted for the degree of Doctor of Philosophy in Physics Gabriela Soledad Vila Supervisor: Dr. Gustavo E. Romero Counsellor: Dr. Pablo D. Mininni Workplace: Instituto Argentino de Radioastronomía Buenos Aires, 2012 UNIVERSIDAD DE BUENOS AIRES Facultad de Ciencias Exactas y Naturales Departamento de Física Modelos radiativos para jets en binarias de rayos X Tesis presentada para optar al título de Doctor de la Universidad de Buenos Aires en el área Ciencias Físicas Gabriela Soledad Vila Director de Tesis: Dr. Gustavo E. Romero Consejero de Estudios: Dr. Pablo D. Mininni Lugar de Trabajo: Instituto Argentino de Radioastronomía Buenos Aires, 2012 This work has been awarded the Carlos M. Varsavsky Prize to the Best PhD Thesis on Astronomy and Astrophysics in Argentina 2010-2012, granted by the Astronomical Society of Argentina. Este trabajo ha sido galardonado con el Premio Carlos M. Varsavsky a la Mejor Tesis Doctoral en Astronomía y Astrofísica de la Argentina 2010-2012, otorgado por la Asociación Argentina de Astronomía. ABSTRACT Radiative models for jets in X-ray binaries An outstanding feature of astrophysical accreting sources at all scales in the Universe is the production of jets - collimated, bipolar, extended flows of matter and electromagnetic field ejected from the surroundings of a rotating object. Microquasars are X-ray binaries that produce relativistic jets. Jets in microquasars emit along the whole electromagnetic spectrum. The radiation is non-thermal; this reveals that jets accelerate particles up to relativistic energies. Understanding the origin of the emission is, then, one way to probe the interior of jets. In this thesis we develop a lepto-hadronic model for the electromagnetic radiation from jets in microquasars with low-mass companion stars. We con- sider the interaction of relativistic particles with matter, radiation, and mag- netic field, and obtain broadband spectral energy distributions. We investi- gate how the shape of the spectrum changes as the parameters that model the conditions in the jet are varied within the constraints imposed by theory and observations. We present general results, as well as applications to some spe- cific systems. Motivated by the growing volume and quality of the data now becoming available at high and very high energies, we carefully analyse the predictions of the model in the gamma-ray band. The results will be directly tested in the near future with the present and forthcoming space-borne and terrestrial gamma-ray telescopes. Keywords: microquasars; jets; non-thermal radiation; gamma rays; X-ray binaries: individual: GX 339-4; X-ray binaries: individual: XTE J1118+480. vii RESUMEN Modelos radiativos para jets en binarias de rayos X Una propiedad notable de los sistemas astrofísicos acretantes a toda escala en el Universo es la producción de jets - flujos colimados, bipolares y extendi- dos de materia y campo electromagnético eyectados desde las cercanías de un objeto en rotación. Los microcuasares son binarias de rayos X con jets. Los jets en microcuasares emiten a lo largo de todo el espectro electromagnético. La radiación es no térmica, lo que indica que los jets aceleraran partículas hasta energías relativistas. Comprender el origen de la emisión electromagnética es, entonces, una de las maneras de explorar el interior de los jets. En esta tesis se desarrolla un modelo lepto-hadrónico para la radiación electromagnética de jets en microcuasares con estrellas compañeras de baja masa. Se considera la interacción entre las partículas relativistas con materia, radiación y campo magnético para obtener espectros de banda ancha. Se in- vestiga cómo se modifica la forma de los espectros al variar los valores de los parámetros que modelan las condiciones físicas en los jets, dentro de las cotas impuestas por teoría y observaciones. Se presentan resultados generales y apli- caciones a sistemas específicos. En vista de la creciente calidad y cantidad de los datos que es actualmente posible obtener a altas y muy altas energías, se analizan en detalle las predicciones del modelo en la banda de rayos gamma. Los resultados podrán ser directamente contrastados en el futuro cercano con las observaciones de telescopios de rayos gamma espaciales y terrestres de pre- sente y futura generación. Palabras clave: microcuasares; jets; radiación no térmica; rayos gamma; binarias de rayos X: GX 339-4; binarias de rayos X: XTE J1118+480. ix ACKNOWLEDGEMENTS The vocabulary of pages that follow is made up of formulas, graphics, and specialised jargon. Writing down the results of the work of five years using those tools has been, however, easier than putting down in everyday words my gratitude to whom accompanied me in the process. These paragraphs are my unsatisfactory attempt. To Gustavo Romero, my supervisor and my friend. For all the opportunities you have given me, that are so many! For trusting that I’d be able to cope with every challenge (and for accepting it when I refused to take some of them). For always caring about my career (and that of all your students) in spite of your tiredness and your other obligations; your unlimited commitment is for me a great example. For caring also for my development as a person. For the many pieces of advice you gave me, and for creating the necessary trust for me to ask for them. Thank you, Gustavo. To the members of the GARRA group. Very special thanks to Paula, for her friendship and her help during my first years in La Plata. Also to Matías, for the discussions and for sharing his knowledge with me, and to Leonardo, for his great human qualities. And mostly to the girls, Florencia, María Victoria, and Daniela, for their company and the joy they bring to the office hours. To the Instituto Argentino de Radioastronomía and the Facultad de Ciencias Exactas y Naturales of the Universidad de Buenos Aires. To all my teachers and professors. I am proud of being the product of Argentinian public education. To the members of the examining committee, Drs. Rafael Ferraro, Josep M. Paredes, and Leonardo J. Pellizza. My special acknowledgement to Dr. Paredes for travelling from Barcelona to attend the defense of this thesis. To Valentí Bosch-Ramon, for his friendship and his invaluable advice on scientific matters. xi To Prof. Dr. Felix Aharonian, for the opportunity of working in his group at the Max-Planck-Institut für Kernphysik, in Heidelberg. To my friends and colleagues Alejandra and Cecilia, for their friendship, their support, and the mutual understanding. To Ale very specially, as well, for the three years of shared household chores. To my friends from childhood and teenage years, for still being my friends despite my months (even years) of absence. Thinking of you immediately puts my whole life in perspective; it helps me become conscious of the long road I’ve walked since the first day at “the 23” (with Lili) till today, passing by the classrooms of the Excelsior (with Claudia, Mariana, and Paola), and with a stop now and then on Saturday afternoons to buy magazines and cassettes (with Samanta). Thank you, friends. More than anyone, to my parents Alicia and Ernesto, the eternal rocks beneath. For letting me choose my future freely, and for teaching me that the only way to achieve what I wish is through work and effort. All I’ve reached is for you. To my grandparents, because their love and the memories of my childhood have definitely shaped my nature. Those of them who cannot see me today, I guess would be proud of me. And to Nicolás, for his company, his patience, his help, his support, his en- couragement, his trust, and for teaching me almost everything else I still had to learn. Tu n’es encore pour moi qu’un petit garçon tout semblable à cent mille petits garçons. Et je n’ai pas besoin de toi. Et tu n’as pas besoin de moi non plus. Je ne suis pour toi qu’un renard semblable à cent mille renards. Mais, si tu m’apprivoises, nous aurons besoin l’un de l’autre. Tu seras pour moi unique au monde. Je serai pour toi unique au monde... Gabriela AGRADECIMIENTOS El vocabulario de las páginas que siguen se compone de fórmulas, gráficos y términos especializados. Redactar los resultados del trabajo de cinco años usando esas herramientas ha resultado, sin embargo, más fácil que poner en palabras sencillas mi agradecimiento a aquellos que me acompañaron en el proceso. Estos párrafos son mi insatisfactorio intento en ese sentido. A Gustavo Romero, mi director y mi amigo. Por todas las oportunidades que me has dado, ¡que son tantas! Por confiar en que iba a poder con cada desafío (y por aceptarlo cuando no quise afrontar alguno). Por ocuparte siem- pre de mi carrera (y la de todos tus estudiantes) a pesar del cansancio y tus demás obligaciones; tu compromiso y dedicación sin límites es para mi un gran ejemplo. Por preocuparte por mi crecimiento como persona, a la par de mi crecimiento como científica. Por los muchos consejos que me diste, y por que exista la confianza necesaria para pedírtelos. Gracias Gustavo. A los integrantes del grupo GARRA. Gracias muy especiales a Paula, por su amistad y su ayuda en mis primeros años en La Plata. También a Matías, por las discusiones y por compartir conmigo sus conocimientos, y a Leonardo por su gran calidad humana. Y sobre todo a las chicas, Florencia, María Victoria y Daniela, por su compañía y por la alegría que aportan a las horas de oficina. Al Instituto Argentino de Radioastronomía y a la Facultad de Ciencias Exac- tas y Naturales de la Universidad de Buenos Aires.
Load more

Recommended publications
  • Studying the ISM at ∼ 10 Pc Scale in NGC 7793 with MUSE - I
    Astronomy & Astrophysics manuscript no. dellabruna_2020 c ESO 2020 February 24, 2020 Studying the ISM at ∼ 10 pc scale in NGC 7793 with MUSE - I. Data description and properties of the ionised gas Lorenza Della Bruna1, Angela Adamo1, Arjan Bik1, Michele Fumagalli2; 3; 4, Rene Walterbos5, Göran Östlin1, Gustavo Bruzual6, Daniela Calzetti7, Stephane Charlot8, Kathryn Grasha9, Linda J. Smith10, David Thilker11, and Aida Wofford12 1 Department of Astronomy, Oskar Klein Centre, Stockholm University, AlbaNova University Centre, SE-106 91 Stockholm, Swe- den 2 Institute for Computational Cosmology, Durham University, South Road, Durham, DH1 3LE, UK 3 Centre for Extragalactic Astronomy, Durham University, South Road, Durham, DH1 3LE, UK 4 Dipartimento di Fisica G. Occhialini, Università degli Studi di Milano Bicocca, Piazza della Scienza 3, 20126 Milano, Italy 5 Department of Astronomy, New Mexico State University, Las Cruces, NM, 88001, USA 6 Instituto de Radioastronomía y Astrofísica, UNAM, Campus Morelia, Michoacan, C.P. 58089, México 7 Department of Astronomy, University of Massachusetts, Amherst, MA 01003, USA 8 Sorbonne Université, CNRS, UMR7095, Institut d’Astrophysique de Paris, F-75014, Paris, France 9 Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 2611, Australia 10 Space Telescope Science Institute and European Space Agency, 3700 San Martin Drive, Baltimore, MD 2121, USA 11 Department of Physics and Astronomy, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA 12 Instituto de Astronomía, Universidad Nacional Autónoma de México, Unidad Académica en Ensenada, Km 103 Carr. Tijuana−Ensenada, Ensenada 22860, México Received XXX / Accepted YYY ABSTRACT Context. Studies of nearby galaxies reveal that around 50% of the total Hα luminosity in late-type spirals originates from diffuse ionised gas (DIG), which is a warm, diffuse component of the interstellar medium that can be associated with various mechanisms, the most important ones being ’leaking’ HII regions, evolved field stars, and shocks.
    [Show full text]
  • Exótico Cielo Profundo 9
    9 El escultor de galaxias Sculptor (Scl) Sculptoris. Escultor. · Exótico Cielo Profundo 9 de Rodolfo Ferraiuolo y Enzo De Bernardini Constelación Sculptor (Scl) Época Comienzos de la Primavera Austral Blanco 1 NGC 55 NGC 131 NGC 134 NGC 150 HD 4113 HD 4208 Objetos NGC 253 NGC 289 NGC 288 NGC 300 SDEG NGC 7793 El comienzo de la primavera austral es una gran ocasión para explorar algunos magníficos objetos de Sculptor, constelación creada en el año 1752 por el astrónomo rumano-francés Nicolai-Ludovici De La Caille, más conocido como Nicolás-Louis de Lacaille. Dentro de sus límites encontramos a, la mayoría de una veintena de galaxias, del tipo tardío, de un cercano (el más próximo al Grupo Local) y pequeño grupo, bautizado en 1959 por el astrónomo francés G. de Vaucouleurs como Grupo de Sculptor y, en 1960 por el astrónomo argentino J. L. Sérsic, Grupo del Polo Sur Galáctico, debido a que sus miembros se localizan agrupados en dirección al Polo Sur Galáctico. De este sugestivo grupo elegimos algunas hermosas galaxias que, estudiaremos junto a otros interesantes objetos más, como el cúmulo globular NGC 288, el cúmulo abierto Blanco 1, otras galaxias lejanas y, como curiosidad ya que no es habitual en la sección, veremos un par de brillantes estrellas con exoplanetas. Nuestro punto de partida será al Sur de la constelación, donde estudiaremos a NGC 300. Esta bonita galaxia espiral, clase SA(s)d, es miembro del Grupo del Polo Galáctico Sur y, fue descubierta por J. Dunlop en el año 1826, unos 8 años antes que J.
    [Show full text]
  • Parameters of Selected Central Stars of Planetary Nebulae from Consistent Optical and Uv Spectral Analysis
    PARAMETERS OF SELECTED CENTRAL STARS OF PLANETARY NEBULAE FROM CONSISTENT OPTICAL AND UV SPECTRAL ANALYSIS Cornelius Bernhard Kaschinski PARAMETERS OF SELECTED CENTRAL STARS OF PLANETARY NEBULAE FROM CONSISTENT OPTICAL AND UV SPECTRAL ANALYSIS Dissertation Ph.D. Thesis an der Ludwig–Maximilians–Universitat¨ (LMU) Munchen¨ at the Ludwig–Maximilians–University (LMU) Munich fur¨ den Grad des for the degree of Doctor rerum naturalium vorgelegt von submitted by Cornelius Bernhard Kaschinski Munchen,¨ 2013 1st Evaluator: Prof. Dr. A. W. A. Pauldrach 2nd Evaluator: Prof. Dr. Barbara Ercolano Date of oral exam: 25.4.2013 Contents Contents vii List of Figures xii List of Tables xiii Zusammenfassung xv Abstract xvii 1 Introduction 1 1.1 Hot Stars . 1 1.1.1 Evolution of hot stars . 1 1.2 Impact of massive stars on the evolution of stellar clusters . 5 1.3 Motivation of this thesis . 5 1.4 Organization of this thesis . 8 2 Radiation-driven winds of hot luminous stars 11 XVII. Parameters of selected central stars of PN from consistent optical and UV spectral analysis and the universality of the mass–luminosity relation 2.1 Introduction . 12 2.2 Methods . 15 2.2.1 Parameter determination using hydrodynamic models and the UV spectrum . 15 2.2.2 Parameter determination using optical H and He lines . 18 2.2.3 Combined analysis . 19 2.3 Implementation of Stark broadening in the model atmosphere code WM-basic . 19 2.4 CSPN observational material . 25 2.5 Consistent optical and UV analysis of the CSPNs NGC 6826 and NGC 2392 . 25 2.5.1 NGC 6826 .
    [Show full text]
  • The Structure & Stellar Populations of Nuclear Star Clusters in Late-Type
    UC Irvine UC Irvine Electronic Theses and Dissertations Title The Structure and Stellar Populations of Nuclear Star Clusters in Late-Type Spiral Galaxies Permalink https://escholarship.org/uc/item/3634g66n Author Carson, Daniel James Publication Date 2016 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA, IRVINE The Structure & Stellar Populations of Nuclear Star Clusters in Late-Type Spiral Galaxies DISSERTATION submitted in partial satisfaction of the requirements for the degree of DOCTOR OF PHILOSOPHY in Physics by Daniel J. Carson Dissertation Committee: Professor Aaron Barth, Chair Associate Professor Michael Cooper Professor James Bullock 2016 Portion of Chapter 1 c 2015 The Astronomical Journal Chapter 2 c 2015 The Astronomical Journal Chapter 3 c 2015 The Astronomical Journal Portion of Chapter 5 c 2015 The Astronomical Journal All other materials c 2016 Daniel J. Carson TABLE OF CONTENTS Page LIST OF FIGURES iv LIST OF TABLES vi ACKNOWLEDGMENTS vii CURRICULUM VITAE viii ABSTRACT OF THE DISSERTATION x 1 Introduction 1 2 HST /WFC3 data 9 2.1 SampleSelection ................................. 9 2.2 DescriptionofObservations . 10 2.3 DataReduction.................................. 14 3 Analysis of Structural Properties 17 3.1 Surface Brightness Profile Fitting . 17 3.1.1 PSFModels................................ 18 3.1.2 FittingMethod .............................. 19 3.1.3 Comparison with ISHAPE ......................... 21 3.1.4 1DRadialProfiles ............................ 22 3.1.5 Uncertainties in Cluster Parameters . 25 3.2 Results....................................... 29 3.2.1 SingleBandResults ........................... 29 3.2.2 PanchromaticResults........................... 40 3.2.3 Stellar Populations . 46 3.3 CommentsonIndividualObjects . 51 3.3.1 IC342................................... 51 3.3.2 M33 ...................................
    [Show full text]
  • List of Publications (06/2021)
    Prof. Dr. Eva K. Grebel, Astronomisches Rechen-Institut, Zentrum f¨urAstronomie der Universit¨at Heidelberg, M¨onchhofstr. 12{14, D-69120 Heidelberg, Germany List of Publications (06/2021) A. Refereed publications (443) . 1 B. Reviews (34) . 47 C. Conference proceedings etc. (175) 50 D. Abstracts (141) . 66 E. Books (2) . 77 In publications with my students or postdocs their names are underlined when this work was completed (or partially carried out) while they held their position with me. A. Refereed Publications 1. Menon, S.H., Grasha, K., Elmegreen, B.G., Federrath, C., Krumholz, M.R., Calzetti, D., S´anchez, N., Linden, S.T., Adamo, A., Messa, M., Cook, D.O., Dale, D.A., Grebel, E.K., Fumagalli, M., Sabbi, E., Johnson, K.E., Smith, L.J., & Kennicutt, R.C. The Dependence of the Hierarchical Distribution of Star Clusters on Galactic En- vironment 2021, MNRAS, submitted 2. D´ek´any, I., Grebel, E.K., & Pojmanski, G. Metallicity estimation of RR Lyrae stars from their I-band light curves 2021, ApJ, submitted 3. Gatto, M., Ripepi, V., Bellazzini, M., Tosi, M., Cignoni, M., Tortora, C., Leccia, S., Clementini, G., Grebel, E.K., Longo, G., Marconi, M., & Musella, I. STEP Survey II: Structural Analysis of 170 star clusters in the SMC 2021, MNRAS, submitted 4. Orozco-Duarte, R., Wofford, A., Vidal-Garc´ıa, A., Bruzual, G., Charlot, S., Krumholz, M., Hannon, S., Lee, J., Wofford, T., Fumagalli, M., Dale, D., Messa, M., Grebel, E.K., Smith, L., Grasha, K., & Cook, D. Synthetic photometry of OB star clusters with stochastically sampled IMFs: anal- ysis of models and HST observations 2021, MNRAS, submitted 5.
    [Show full text]
  • The Bright Sharc Survey: the Cluster Catalog1 Ak Romer2 and Rc Nichol3,4
    THE ASTROPHYSICAL JOURNAL SUPPLEMENT SERIES, 126:209È269, 2000 February ( 2000. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE BRIGHT SHARC SURVEY: THE CLUSTER CATALOG1 A. K. ROMER2 AND R. C. NICHOL3,4 Department of Physics, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA 15213; romer=cmu.edu, nichol=cmu.edu B. P. HOLDEN2,3 Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637; holden=oddjob.uchicago.edu M. P. ULMER AND R. A. PILDIS Department of Physics and Astronomy, Northwestern University, 2131 North Sheridan Road, Evanston, IL 60207; ulmer=ossenu.astro.nwu.edu A. J. MERRELLI2 Department of Physics, Carnegie Mellon University, 5000. Forbes Avenue, Pittsburgh, PA 15213; merrelli=andrew.cmu.edu C. ADAMI4 Department of Physics and Astronomy, Northwestern University, 2131 North Sheridan Road, Evanston, IL 60207;adami=lilith.astro.nwu.edu; and Laboratoire d Astronomie Spatiale, Traverse du Siphon, 13012 Marseille, France D. J. BURKE3 AND C. A. COLLINS3 Astrophysics Research Institute, Liverpool John Moores University, Twelve Quays House, Egerton Wharf, Birkenhead, L41 1LD, UK; djb=astro.livjm.ac.uk, cac=astro.livjm.ac.uk A. J. METEVIER UCO/Lick Observatory, University of California, Santa Cruz, CA 95064; anne=ucolick.org R. G. KRON Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637; rich=oddjob.uchicago.edu AND K. COMMONS2 Department of Physics and Astronomy, Northwestern University, 2131 North Sheridan Road, Evanston, IL 60207; commons=lilith.astro.nwu.edu Received 1999 April 12; accepted 1999 August 23 ABSTRACT We present the Bright SHARC (Serendipitous High-Redshift Archival ROSAT Cluster) Survey, which is an objective search for serendipitously detected extended X-ray sources in 460 deep ROSAT PSPC pointings.
    [Show full text]
  • (M/LB)N 9 Ma/La (At the Last Observed Velocity Point) Is Found for the Individual Galaxies
    HI STUDIES OF THE SCULPTOR GROUP GALAXIES Claude Carignan, UniversitC de MontrCal and Daniel Puche, Very Large Array, NRAO ABSTRACT Results from large-scale mapping of the HI gas in the Sculptor group are presented. From our kinematic analysis, a mean global (M/LB)N 9 Ma/La (at the last observed velocity point) is found for the individual galaxies. This is only a factor - 10 smaller than the (M/LB)~~~II 90 Mo/Lo derived from a dynamical study of the whole group. The parameters derived from the mass models sug- gest that most of the unseen matter has to be concentrated around the luminous galaxies. Under the assumption that the Sculptor group is a virialized system and that all the mass is associated with the galaxies, an upper limit of - 40 kpc is derived for the size of the dark halos present in the five late-type spirals of the group. 1. Introduction Dynamical studies of individual galaxies, groups of galaxies, and clusters of galaxies have led to a large variety of sometimes contradictory values of dynamical mass-to-light ratios (MILB).The present situation can be summarized as follows. According to the scale considered, determinations of M/LB range from 1 to 500 MB/La. In this interval, the most cited numbers are N 2-10 for individual galaxies (from rotation curves of spirals), N 30-100 for binaries and small groups, and N 200 for rich clusters (Faber and Gallagher 1979). The obvious conclusion is that there is a large quantity of dark matter (DM) present in these systems.
    [Show full text]
  • Stellar Populations and Star Formation Histories of the Nuclear Star Clusters
    MNRAS 480, 1973–1998 (2018) doi:10.1093/mnras/sty1985 Advance Access publication 2018 July 24 Stellar populations and star formation histories of the nuclear star clusters in six nearby galaxies Nikolay Kacharov,1† Nadine Neumayer,1 Anil C. Seth,2 Michele Cappellari,3 Richard McDermid,4,5 C. Jakob Walcher6 and Torsten Boker¨ 7 Downloaded from https://academic.oup.com/mnras/article-abstract/480/2/1973/5057883 by Macquarie University user on 07 December 2018 1Max Planck Institut fur¨ Astronomie, Konigstuhl¨ 17, D-69117 Heidelberg, Germany 2Department of Physics and Astronomy, University of Utah, 115 South 1400 East, Salt Lake City, Utah 84112, USA 3Sub-Department of Astrophysics, Department of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK 4Department of Physics and Astronomy, Macquarie University, Sydney, NSW 2109, Australia 5Australian Gemini Office, Australian Astronomical Observatory, PO Box 915, Sydney, NSW 1670, Australia 6Leibniz-Institut fur¨ Astrophysik Potsdam (AIP), An der Sternwarte 16, D-14482, Potsdam, Germany 7European Space Agency, c/o STScI, 3700 San Martin Drive, Baltimore, MD 21218, USA Accepted 2018 July 23. Received 2018 July 18; in original form 2018 June 7 ABSTRACT The majority of spiral and elliptical galaxies in the Universe host very dense and compact stellar systems at their centres known as nuclear star clusters (NSC). In this work, we study the stellar populations and star formation histories (SFH) of the NSCs of six nearby galaxies with 9 stellar masses ranging between 2 and 8 × 10 M (four late-type spirals and two early-types) with high-resolution spectroscopy.
    [Show full text]
  • Thermal X-Ray Emission from Young Type Ia Supernova Remnants
    Thermal X-ray Emission From Young Type Ia Supernova Remnants Carles Badenes Montoliu Mem`oria presentada per optar al grau de Doctor Director: Eduard Bravo Guil Departament de F´ısica i Enginyeria Nuclear Universitat Polit`ecnica de Catalunya Institut d'Estudis Espacials de Catalunya Barcelona, Maig 2004 A la Nuria,´ per fer possibles tantes coses... Was ich weiss, kann jeder wissen, mein Herz habe ich allein. El que jo s´e, ho pot saber qualsevol, el meu cor nom´es el tinc jo. Johann Wolfgang von Goethe (1749-1832). Werther. Thermal X-ray Emission From Young Type Ia Supernova Remnants Carles Badenes Abstract The relationship between Type Ia supernovae and the thermal X-ray emission from their young supernova remnants is explored using one dimensional hydrodynamics and self- consistent ionization and electron heating calculations coupled to a spectral code. The interaction with the ambient medium is simulated for a grid of supernova explosion models which includes all the physical mechanisms currently under debate. The differences in density profile and chemical composition of the ejecta for each supernova explosion model have a profound impact on the hydrodynamic evolution, plasma ionization and emitted thermal X-ray spectra of the supernova remnant, even several thousand years after the explosion. This has two important consequences. First, new possibilities are opened for the use of the high quality X-ray observations of Type Ia supernova remnants as a tool to study supernova explosions. Second, it follows immediately that an accurate analysis of such observations is not possible unless the characteristics of the supernova explosion are considered in some detail.
    [Show full text]
  • 82924833.Pdf
    MNRAS 468, 492–500 (2017) doi:10.1093/mnras/stx410 Advance Access publication 2017 February 17 Physical properties of the first spectroscopically confirmed red supergiant stars in the Sculptor Group galaxy NGC 55 L. R. Patrick,1,2,3‹ C. J. Evans,3,4 B. Davies,5 R-P. Kudritzki,6,7 A. M. N. Ferguson,3 M. Bergemann,8 G. Pietrzynski´ 9,10 and O. Turner3 1Instituto de Astrof´ısica de Canarias, E-38205 La Laguna, Tenerife, Spain 2Universidad de La Laguna, Dpto Astrof´ısica, E-38206 La Laguna, Tenerife, Spain 3Institute for Astronomy, University of Edinburgh, Royal Observatory Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK 4UK Astronomy Technology Centre, Royal Observatory Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK 5Astrophysics Research Institute, Liverpool John Moores University, Liverpool Science Park ic2, 146 Brownlow Hill, Liverpool L3 5RF, UK 6Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA 7University Observatory Munich, Scheinerstr. 1, D-81679 Munich, Germany 8Max-Planck Institute for Astronomy, D-69117 Heidelberg, Germany 9Departamento de Astronom´ıa, Universidad de Concepcion,´ Casilla 160-C, Concepcion,´ Chile 10Nicolaus Copernicus Astronomical Centre, Polish Academy of Sciences, Bartycka 18, PL-00-716 Warszawa, Poland Accepted 2017 February 14. Received 2017 February 14; in original form 2016 December 19 ABSTRACT We present K-band Multi-Object Spectrograph (KMOS) observations of 18 red supergiant (RSG) stars in the Sculptor Group galaxy NGC 55. Radial velocities are calculated and are shown to be in good agreement with previous estimates, confirming the supergiant nature of the targets and providing the first spectroscopically confirmed RSGs in NGC 55.
    [Show full text]
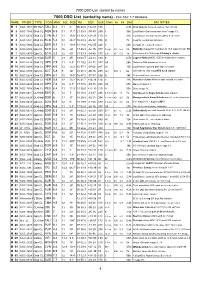
  • DSO List V2 Current
    7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14..
    [Show full text]
  • The GHOSTS Survey. II. the Diversity of Halo Color and Metallicity Profiles of Massive Disk Galaxies
    Mon. Not. R. Astron. Soc. 000, 1{30 (2015) Printed 20 January 2016 (MN LATEX style file v2.2) The GHOSTS survey. II. The diversity of Halo colour and Metallicity Profiles of Massive Disk Galaxies ? Antonela Monachesi1 y, Eric F. Bell2, David J. Radburn-Smith3, Jeremy Bailin4;5, Roelof S. de Jong6, Benne Holwerda7, David Streich6, Grace Silverstein4 1Max Planck Institute for Astrophysics, Karl-Schwarzschild-Str. 1, Garching D-85748, Germany 2Department of Astronomy, University of Michigan, 311 West Hall, 1085 South University Ave., Ann Arbor, MI 48109, USA 3Department of Astronomy, University of Washington, Seattle, WA 98195,USA 4Department of Physics and Astronomy, University of Alabama, Box 870324, Tuscaloosa, AL, 35487, USA 5National Radio Astronomy Observatory, P.O. Box 2, Green Bank, WV, 24944, USA 6Leibniz-Institut f¨urAstrophysik Potsdam, D-14482 Potsdam, Germany 7University of Leiden, Sterrenwacht Leiden, Niels Bohrweg 2, NL-2333 CA Leiden, The Netherlands ABSTRACT We study the stellar halo colour properties of six nearby massive highly inclined disk galaxies using HST ACS and WFC3 observations in both F 606W and F 814W fil- ters from the GHOSTS survey. The observed fields probe the stellar outskirts out to projected distances of ∼ 50 { 70 kpc from their galactic centre along the minor axis. The 50% completeness levels of the colour magnitude diagrams are typically at two mag below the tip of the red giant branch. We find that all galaxies have ex- tended stellar haloes out to ∼ 50 kpc and two out to ∼ 70 kpc. We determined the halo colour distribution and colour profile for each galaxy using the median colours of stars in the RGB.
    [Show full text]