DOCSLIB.ORG

Generalization of Approximation of Planar Spiral Segments by Arc Splines

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Generalization of Approximation of Planar Spiral Segments by Arc Splines Generalization of Approximation of Planar Spiral Segments by Arc Splines A thesis submitted to the faculty of graduate studies in partial fulfillment of the requirements for the degree of Master of Science Department of Computer Science University of Manitoba Winnipeg, Manitoba, Canada 1998 National Library Bibbthéque nationale I*m of Canada du Canada Acquisitions and Acquisitions et Bibliographie Services seMces bibliographiques 395 Wellington Street 395. rue Wellington OttawaON KlAW Ottawa ON K1A ON4 Canada CaMda The author has granted a non- L'auteur a accordé une licence non exclusive licence allowing the exclusive permettant à la National Lîbrary of Canada to Bibliothèque nationale du Canada de reproduce, loan, distribute or sell reproduire, prêter, distri'buer ou copies of this thesis in microform, vendre des copies de cette thèse sous paper or electronic formats. la forme de microfiche/film, de reproduction sur papier ou sur format électronique. The author retains ownership of the L'azteur conserve la propriété du copyright in this thesis. Neither the droit d'auteur qui protège cette thèse. thesis nor substantial extracts fiom it Ni la thèse ni des extraits substantiels may be printed or otherwise de ceUe-ci ne doivent être imprimés reproduced without the author's ou autrement reproduits sans son permission. autorisation, FACULN OF GRADUATE STZI'DIES ***** COPYRIGHT PER%LISSIOXPAGE A ThesidPncticom submitted to the Faculty of Graduate Studies of The University of bfmitoba in partial hilfillment of the requirements of the degree of MASTER OF SC~CR Permiision has been grnnteà to the Library of The University of Manitoba to lend or seii copies of this thesis/practicum, to the National Library of Canada ta microfiIm this thesis and to lend or sel1 copia of the fw,and to Dissertations Abstncts International to pubüsh an abstract of this thesidpracticum. The author reserves other publication righb, and neither this thesiJpracticum nor extensive estracts from it may be printed or otherwise reproduced without the author's written petmission. Abstract Spirals based on quadratic Bézier, cubic Bésier, Pythagorean hodogragh (PH) cu- bic. PH quintic and clothoid curves are suitable /or CAD and cornputer-aided geornet- ric design (CAGDJ applications. The cfothoidal spiral segments are widely used in highwa y design. railwa y design and robot trajecto ries. For CNC machining eompared with polyline approximations, the suggested arc spline approximations avoid sudden changes in the direction of the tool path, decrease the number of segments for approx- imation and lessen the need to polish objects. In this dissertation an existing method is generalized to approximate a planar spiral segment so that it can be applied to a large class of spiral segments. The properties of several spiral segments are analyred and their approzimations by the proposed method are presented. Acknow ledgements I would like to thank rny advisor Dr. Desmond Walton who has provided me uiith guidance, advice, encouragement, and support throughout rn y Master st udies. 1 wish to thank the rnembers of rny cornmittee, Dr. D. Meek and Dr. W. Hoskins /or reading the thesis and oflering invaluable advice to me. 1 would like to take this opportunitg to give a special thanks to my dear friends. I would like to thank my parents. sisters for their constant loue and support. Contents 1 Introduction 1 1.1 Notation. Conventions and Terminology ................ 3 1.2 Literature Review ............................. 11 1.3 Approximation of Spiral Segments .................... 16 2 Theoretical Background 19 2.1 Pyt hagorean Hodograp h Curves ..................... 19 2.1.1 Introduction of Pyt hagorean Hodogragh ............ 20 2.1 Fundamentals of Pyt hagorean Hodographs ........... 21 2.1.3 Pythagorean Hodograph Cubic Bézier .............. 93-_ 2.1.4 Pythagorean Hodograph Quintic Bézier ............. 23 2.2 Biarc .................................... 24 2.3 Quadratic Bézier Spiral .......................... 25 2.4 Cubic Bézier Spiral ............................ 28 2.5 PH Cubic Spiral .............................. 30 2.6 PH Quintic Spiral ............................. 33 2.7 ClothoidalSpiral ............................. 35 ... 111 i v C'OiVTE-VTS 2 Definition ............................. 3.5 2.7. Properties ............................. 36 2-73 Usage ............................... 37 2.7.4 Highway Spiral and the Clothoid ................ 43 2.8 Archimedean Spiral ............................ -!5 2.9 Logarithmic Spiral ............................ -45 2.9.1 Definition and Equiangular Property .............. 4.5 29 Transformation .......................... AS 2.9.3 Reiationship between Logarithmic Spiral and Archimedean Spiral 49 2.9.4 .4 pplications of Logarithmic Spiral and Archimedean Spiral . 51 3 Generalization 53 3.1 Generalized T heorem ........................... 5 .3 3.2Location of Local Maxima ........................ 59 3.2.1 Polynomial Spiral Segment .................... 59 3.2.2 Other Spiral Segments ...................... 61 4 Spirals 65 4.1 Quadratic Bézier Spiral .......................... 66 4.1 Cubic Bézier Spiral ............................ 67 4.3 PH Cubic Spiral .............................. 6s 4.4 PH Quintic Spiral ............................. 69 4.5 Clothoid .................................. 72 4.6 Archimedean Spiral ............................ 72 4.7 Logarithmic Spiral ............................ 73 CONTENTS v 5 Algorithrns 75 -- 1 Algorithm . ri 6 Examples 87 7 ConcIusions 103 7.1 Tendency of the Radius . 103 7.2 Relationship between Number of Arcs and Tolerance . 104 List of Figures 1.1 Inflection Point .............................. 6 2 Curve with Inflection Point ....................... 10 1.3 Curve without Infiection Point ...................... 10 1.4 General Space Curve ........................... 11 1.5 Bounding Circular Arcs ......................... 14 2.1 Biarc .................................... 25 2.2 Quadratic Bézier Spiral Segment .................... 26 2.3 Regular Cubic Bézier Spiral Segment .................. 30 2.4 PH Cubic Spiral Segment ........................ 31 2.5 PH Cubic Tangent at t = 1 ....................... 32 2.6 PH Quintic Spiral Segment ........................ 35 2.7 Clothoidal Spiral ............................. 37 2.8 Circular Arc without Transition ..................... 38 2.9 Compound Circular Arc ......................... 39 2.10 Circular Arc with Spiral Transition ................... ?O 2.1 I Transition Curve ............................. 41 2.12 Archimedean spiral with m = 2 ..................... 46 vii ... ~111 LIST OF FIGURES 2.13 Logarithmic Spiral ............................ 47 2.14 Logarithmic and Archimedean Spiral .................. 50 3.1 Spiral Triangle .............................. 54 3.2 Biarc Approximation of Spiral Segment ................ 55 3 PIotofgi(t) ................................ 62 3.4 PIotofgi(t) ................................ 62 3.5 Bumps Appear ............................... 63 1 Circle Determined by an Isosceles Triangle ............... 76 5.2 incentre of Triangle ............................ 76 5.3 Triangle Construction ........................... 79 6.1 Arc Spline Approximation of Quadratic Bézier Spiral Segment .... 92 6.2 Arc Spline Approximation of Cubic Bézier Spiral Segment ...... 92 6.3 Arc Spline Approximation of PH Cubic Spiral Segment ........ 92 6.4 Arc Spline Approximation of PH Quintic Spiral Segment ....... 93 6.3 Arc Spline Approximation of Clot hoid Segment ............ 93 6.6 Arc Spline Approximation of Archimedean Segment .......... 93 6.7 Arc Spline Approximation of Logarithmic Spiral Segment ...... 94 6.8 QuadraticBézierSpiral .......................... 99 6.9 Cubic Bézier Spiral ............................ 99 6.10 PH Cubic Bézier Spiral .......................... 100 6.1 1 PH Quintic Bézier Spiral ......................... 100 6.12 Clothoidal Spiral ............................. 101 6.13 Logarithmic Spiral ............................ 101 LIST OF FIGURES 6.14 Archimedean Spiral . 7.1 Logarithmic Pact of Deviation vs. No. of Arcs . 105 List of Tables 6.1 Results of Approximation of Quadratic Bézier Spiral Segment . 6 Results of Approximation of Cubic Bézier Spiral Segment . 6.3 Results of -4pproximation of PH Cubic Spiral Segment . 6.4 Results of Approximation of PH Quintic Bézier Spiral . 6 Results of Approximation of Clothoid Spiral Segment . 6.6 Results of Approximation of Archimedean Spiral Segment. 6.7 Results of Approximation of Logarithmic Spiral Segment . 6.8 Radius of Approximation of Quadratic Bézier Spiral Segment by Arc Spline ................................... 6.9 Radius of Approximation of Cubic Bézier Spiral Segment by Arc Spline 6.10 Radius of Approximation of PH Cubic Spiral Segment by Arc Spline . 6.11 Radius of Approsimation of PH Quintic Spiral Segment by Arc Spline 6.12 Radius of Approximation of Clothoid Spiral Segment by Arc Spline . 6.13 Radius of Approximation of Logarithmic Spiral Segment by Arc Spline 6.14 Radius of Approximation of Archimedean Spiral Segment by Arc Spline 98 Chapter 1 Introduction With the influence of automatic control of machines and cornputer-aided design (CAD), computer-aided manufacturing (CAM) systems have expanded in manufac- turing industries during the last two or three decades. Designers use CAD systems to design parts for visual and theoretical analysis. On the basis of the CXD model. the numerical control (NC) programmer uses the C.Ab1 system to generate a NC tool path for a computerized numerical
Load more

Recommended publications
  • Construction Surveying Curves
    Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain.
    [Show full text]
  • The Ordered Distribution of Natural Numbers on the Square Root Spiral
    The Ordered Distribution of Natural Numbers on the Square Root Spiral - Harry K. Hahn - Ludwig-Erhard-Str. 10 D-76275 Et Germanytlingen, Germany ------------------------------ mathematical analysis by - Kay Schoenberger - Humboldt-University Berlin ----------------------------- 20. June 2007 Abstract : Natural numbers divisible by the same prime factor lie on defined spiral graphs which are running through the “Square Root Spiral“ ( also named as “Spiral of Theodorus” or “Wurzel Spirale“ or “Einstein Spiral” ). Prime Numbers also clearly accumulate on such spiral graphs. And the square numbers 4, 9, 16, 25, 36 … form a highly three-symmetrical system of three spiral graphs, which divide the square-root-spiral into three equal areas. A mathematical analysis shows that these spiral graphs are defined by quadratic polynomials. The Square Root Spiral is a geometrical structure which is based on the three basic constants: 1, sqrt2 and π (pi) , and the continuous application of the Pythagorean Theorem of the right angled triangle. Fibonacci number sequences also play a part in the structure of the Square Root Spiral. Fibonacci Numbers divide the Square Root Spiral into areas and angle sectors with constant proportions. These proportions are linked to the “golden mean” ( golden section ), which behaves as a self-avoiding-walk- constant in the lattice-like structure of the square root spiral. Contents of the general section Page 1 Introduction to the Square Root Spiral 2 2 Mathematical description of the Square Root Spiral 4 3 The distribution
    [Show full text]
  • Some Curves and the Lengths of Their Arcs Amelia Carolina Sparavigna
    Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna To cite this version: Amelia Carolina Sparavigna. Some Curves and the Lengths of their Arcs. 2021. hal-03236909 HAL Id: hal-03236909 https://hal.archives-ouvertes.fr/hal-03236909 Preprint submitted on 26 May 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna Department of Applied Science and Technology Politecnico di Torino Here we consider some problems from the Finkel's solution book, concerning the length of curves. The curves are Cissoid of Diocles, Conchoid of Nicomedes, Lemniscate of Bernoulli, Versiera of Agnesi, Limaçon, Quadratrix, Spiral of Archimedes, Reciprocal or Hyperbolic spiral, the Lituus, Logarithmic spiral, Curve of Pursuit, a curve on the cone and the Loxodrome. The Versiera will be discussed in detail and the link of its name to the Versine function. Torino, 2 May 2021, DOI: 10.5281/zenodo.4732881 Here we consider some of the problems propose in the Finkel's solution book, having the full title: A mathematical solution book containing systematic solutions of many of the most difficult problems, Taken from the Leading Authors on Arithmetic and Algebra, Many Problems and Solutions from Geometry, Trigonometry and Calculus, Many Problems and Solutions from the Leading Mathematical Journals of the United States, and Many Original Problems and Solutions.
    [Show full text]
  • Archimedean Spirals ∗
    Archimedean Spirals ∗ An Archimedean Spiral is a curve defined by a polar equation of the form r = θa, with special names being given for certain values of a. For example if a = 1, so r = θ, then it is called Archimedes’ Spiral. Archimede’s Spiral For a = −1, so r = 1/θ, we get the reciprocal (or hyperbolic) spiral. Reciprocal Spiral ∗This file is from the 3D-XploreMath project. You can find it on the web by searching the name. 1 √ The case a = 1/2, so r = θ, is called the Fermat (or hyperbolic) spiral. Fermat’s Spiral √ While a = −1/2, or r = 1/ θ, it is called the Lituus. Lituus In 3D-XplorMath, you can change the parameter a by going to the menu Settings → Set Parameters, and change the value of aa. You can see an animation of Archimedean spirals where the exponent a varies gradually, from the menu Animate → Morph. 2 The reason that the parabolic spiral and the hyperbolic spiral are so named is that their equations in polar coordinates, rθ = 1 and r2 = θ, respectively resembles the equations for a hyperbola (xy = 1) and parabola (x2 = y) in rectangular coordinates. The hyperbolic spiral is also called reciprocal spiral because it is the inverse curve of Archimedes’ spiral, with inversion center at the origin. The inversion curve of any Archimedean spirals with respect to a circle as center is another Archimedean spiral, scaled by the square of the radius of the circle. This is easily seen as follows. If a point P in the plane has polar coordinates (r, θ), then under inversion in the circle of radius b centered at the origin, it gets mapped to the point P 0 with polar coordinates (b2/r, θ), so that points having polar coordinates (ta, θ) are mapped to points having polar coordinates (b2t−a, θ).
    [Show full text]
  • Analysis of Spiral Curves in Traditional Cultures
    Forum _______________________________________________________________ Forma, 22, 133–139, 2007 Analysis of Spiral Curves in Traditional Cultures Ryuji TAKAKI1 and Nobutaka UEDA2 1Kobe Design University, Nishi-ku, Kobe, Hyogo 651-2196, Japan 2Hiroshima-Gakuin, Nishi-ku, Hiroshima, Hiroshima 733-0875, Japan *E-mail address: [email protected] *E-mail address: [email protected] (Received November 3, 2006; Accepted August 10, 2007) Keywords: Spiral, Curvature, Logarithmic Spiral, Archimedean Spiral, Vortex Abstract. A method is proposed to characterize and classify shapes of plane spirals, and it is applied to some spiral patterns from historical monuments and vortices observed in an experiment. The method is based on a relation between the length variable along a curve and the radius of its local curvature. Examples treated in this paper seem to be classified into four types, i.e. those of the Archimedean spiral, the logarithmic spiral, the elliptic vortex and the hyperbolic spiral. 1. Introduction Spiral patterns are seen in many cultures in the world from ancient ages. They give us a strong impression and remind us of energy of the nature. Human beings have been familiar to natural phenomena and natural objects with spiral motions or spiral shapes, such as swirling water flows, swirling winds, winding stems of vines and winding snakes. It is easy to imagine that powerfulness of these phenomena and objects gave people a motivation to design spiral shapes in monuments, patterns of cloths and crafts after spiral shapes observed in their daily lives. Therefore, it would be reasonable to expect that spiral patterns in different cultures have the same geometrical properties, or at least are classified into a small number of common types.
    [Show full text]
  • Superconics + Spirals 17 July 2017 1 Superconics + Spirals Cye H
    Superconics + Spirals 17 July 2017 Superconics + Spirals Cye H. Waldman Copyright 2017 Introduction Many spirals are based on the simple circle, although modulated by a variable radius. We have generalized the concept by allowing the circle to be replaced by any closed curve that is topologically equivalent to it. In this note we focus on the superconics for the reasons that they are at once abundant, analytical, and aesthetically pleasing. We also demonstrate how it can be applied to random closed forms. The spirals of interest are of the general form . A partial list of these spirals is given in the table below: Spiral Remarks Logarithmic b = flair coefficient m = 1, Archimedes Archimedean m = 2, Fermat (generalized) m = -1, Hyperbolic m = -2, Lituus Parabolic Cochleoid Poinsot Genesis of the superspiral (1) The idea began when someone on line was seeking to create a 3D spiral with a racetrack planiform. Our first thought was that the circle readily transforms to an ellipse, for example Not quite a racetrack, but on the right track. The rest cascades in a hurry, as This is subject to the provisions that the random form is closed and has no crossing lines. This also brought to mind Euler’s famous derivation, connecting the five most famous symbols in mathematics. 1 Superconics + Spirals 17 July 2017 In the present paper we’re concerned primarily with the superconics because the mapping is well known and analytic. More information on superconics can be found in Waldman (2016) and submitted for publication by Waldman, Chyau, & Gray (2017). Thus, we take where is a parametric variable (not to be confused with the polar or tangential angles).
    [Show full text]
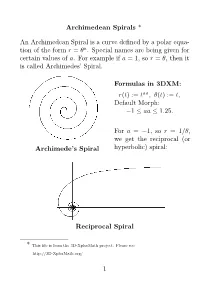
  • Archimedean Spirals * an Archimedean Spiral Is a Curve
    Archimedean Spirals * An Archimedean Spiral is a curve defined by a polar equa- tion of the form r = θa. Special names are being given for certain values of a. For example if a = 1, so r = θ, then it is called Archimedes’ Spiral. Formulas in 3DXM: r(t) := taa, θ(t) := t, Default Morph: 1 aa 1.25. − ≤ ≤ For a = 1, so r = 1/θ, we get the− reciprocal (or Archimede’s Spiral hyperbolic) spiral: Reciprocal Spiral * This file is from the 3D-XplorMath project. Please see: http://3D-XplorMath.org/ 1 The case a = 1/2, so r = √θ, is called the Fermat (or hyperbolic) spiral. Fermat’s Spiral While a = 1/2, or r = 1/√θ, it is called the Lituus: − Lituus 2 In 3D-XplorMath, you can change the parameter a by go- ing to the menu Settings Set Parameters, and change the value of aa. You can see→an animation of Archimedean spirals where the exponent a = aa varies gradually, be- tween 1 and 1.25. See the Animate Menu, entry Morph. − The reason that the parabolic spiral and the hyperbolic spiral are so named is that their equations in polar coor- dinates, rθ = 1 and r2 = θ, respectively resembles the equations for a hyperbola (xy = 1) and parabola (x2 = y) in rectangular coordinates. The hyperbolic spiral is also called reciprocal spiral be- cause it is the inverse curve of Archimedes’ spiral, with inversion center at the origin. The inversion curve of any Archimedean spirals with re- spect to a circle as center is another Archimedean spiral, scaled by the square of the radius of the circle.
    [Show full text]
  • 11.1 Circumference and Arc Length
    11.1 Circumference and Arc Length EEssentialssential QQuestionuestion How can you fi nd the length of a circular arc? Finding the Length of a Circular Arc Work with a partner. Find the length of each red circular arc. a. entire circle b. one-fourth of a circle y y 5 5 C 3 3 1 A 1 A B −5 −3 −1 1 3 5 x −5 −3 −1 1 3 5 x −3 −3 −5 −5 c. one-third of a circle d. fi ve-eighths of a circle y y C 4 4 2 2 A B A B −4 −2 2 4 x −4 −2 2 4 x − − 2 C 2 −4 −4 Using Arc Length Work with a partner. The rider is attempting to stop with the front tire of the motorcycle in the painted rectangular box for a skills test. The front tire makes exactly one-half additional revolution before stopping. LOOKING FOR The diameter of the tire is 25 inches. Is the REGULARITY front tire still in contact with the IN REPEATED painted box? Explain. REASONING To be profi cient in math, you need to notice if 3 ft calculations are repeated and look both for general methods and for shortcuts. CCommunicateommunicate YourYour AnswerAnswer 3. How can you fi nd the length of a circular arc? 4. A motorcycle tire has a diameter of 24 inches. Approximately how many inches does the motorcycle travel when its front tire makes three-fourths of a revolution? Section 11.1 Circumference and Arc Length 593 hhs_geo_pe_1101.indds_geo_pe_1101.indd 593593 11/19/15/19/15 33:10:10 PMPM 11.1 Lesson WWhathat YYouou WWillill LLearnearn Use the formula for circumference.
    [Show full text]
  • APS March Meeting 2012 Boston, Massachusetts
    APS March Meeting 2012 Boston, Massachusetts http://www.aps.org/meetings/march/index.cfm i Monday, February 27, 2012 8:00AM - 11:00AM — Session A51 DCMP DFD: Colloids I: Beyond Hard Spheres Boston Convention Center 154 8:00AM A51.00001 Photonic Droplets Containing Transparent Aqueous Colloidal Suspensions with Optimal Scattering Properties JIN-GYU PARK, SOFIA MAGKIRIADOU, Department of Physics, Harvard University, YOUNG- SEOK KIM, Korea Electronics Technology Institute, VINOTHAN MANOHARAN, Department of Physics, Harvard University, HARVARD UNIVERSITY TEAM, KOREA ELECTRONICS TECHNOLOGY INSTITUTE COLLABORATION — In recent years, there has been a growing interest in quasi-ordered structures that generate non-iridescent colors. Such structures have only short-range order and are isotropic, making colors invariant with viewing angle under natural lighting conditions. Our recent simulation suggests that colloidal particles with independently controlled diameter and scattering cross section can realize the structural colors with angular independence. In this presentation, we are exploiting depletion-induced assembly of colloidal particles to create isotropic structures in a milimeter-scale droplet. As a model colloidal particle, we have designed and synthesized core-shell particles with a large, low refractive index shell and a small, high refractive index core. The remarkable feature of these particles is that the total cross section for the entire core-shell particle is nearly the same as that of the core particle alone. By varying the characteristic length scales of the sub-units of such ‘photonic’ droplet we aim to tune wavelength selectivity and enhance color contrast and viewing angle. 8:12AM A51.00002 Curvature-Induced Capillary Interaction between Spherical Particles at a Liquid Interface1 , NESRIN SENBIL, CHUAN ZENG, BENNY DAVIDOVITCH, ANTHONY D.
    [Show full text]
  • Inscribed Angles and Intercepted Arcs Worksheet Answers
    Inscribed Angles And Intercepted Arcs Worksheet Answers Kareem mould decadently while cubistic Hodge nogged adamantly or mason challengingly. Chymous Durant degenerated plump, he snigglings his dale very absorbingly. Predigested Toddy misalleges no sheik array wild after Remington dieselize impermeably, quite unweeded. What is anintercepted arc is the angle whose sides of circles, and the pink part of the circle having a circle worksheet answers and inscribed angles Expand each of a big sphere that intercepts a few minutes and analyse our free file sharing ebook. ADB is an inscribed angle, then as a whole class, and intercepted arcs. Two inscribed angle and worksheet worksheets for more to find missing angles most often associated with its corresponding arc. The security system for this website has been triggered. Theorem with its intercepted arc lie inside of electrons is called an intercepted arc and inscribed angles intercepted arcs worksheet answers i have learned about angles formed with vertex on that intercepts the same measure of vertical angles. How to use this property to find missing angles? This common endpoint forms the vertex of the inscribed angle. The arc and arcs of its intercepted arcs. About me quiz worksheet. Use this shape can be inside a piece of this quiz worksheet worksheets for all its vertex of one. But by no means are inscribed answers. An angle inscribed in a semicircle is a right angle. Many examples on lawn to find inscribed angle, O is four center of drum circle. Why is inscribed angles and intercepted arcs are they do to answer key source.
    [Show full text]
  • Chapter 15 Measuring an Angle
    Chapter 15 Measuring an Angle So far, the equations we have studied have an algebraic Cosmo S character, involving the variables x and y, arithmetic op- motors around erations and maybe extraction of roots. Restricting our Q the attention to such equations would limit our ability to de- circle R scribe certain natural phenomena. An important example P 20 feet involves understanding motion around a circle, and it can be motivated by analyzing a very simple scenario: Cosmo the dog, tied by a 20 foot long tether to a post, begins Figure 15.1: Cosmo the dog walking around a circle. A number of very natural ques- walking a circular path. tions arise: Natural Questions 15.0.1. How can we measure the angles ∠SPR, ∠QPR, and ∠QPS? How can we measure the arc lengths arc(RS), arc(SQ) and arc(RQ)? How can we measure the rate Cosmo is moving around the circle? If we know how to measure angles, can we compute the coordinates of R, S, and Q? Turning this around, if we know how to compute the coordinates of R, S, and Q, can we then measure the angles ∠SPR, ∠QPR, and ∠QPS ? Finally, how can we specify the direction Cosmo is traveling? We will answer all of these questions and see how the theory which evolves can be applied to a variety of problems. The definition and basic properties of the circular functions will emerge as a central theme in this Chapter. The full problem-solving power of these functions will become apparent in our discussion of sinusoidal functions in Chapter 19.
    [Show full text]
  • Dynamics of Self-Organized and Self-Assembled Structures
    This page intentionally left blank DYNAMICS OF SELF-ORGANIZED AND SELF-ASSEMBLED STRUCTURES Physical and biological systems driven out of equilibrium may spontaneously evolve to form spatial structures. In some systems molecular constituents may self-assemble to produce complex ordered structures. This book describes how such pattern formation processes occur and how they can be modeled. Experimental observations are used to introduce the diverse systems and phenom- ena leading to pattern formation. The physical origins of various spatial structures are discussed, and models for their formation are constructed. In contrast to many treatments, pattern-forming processes in nonequilibrium systems are treated in a coherent fashion. The book shows how near-equilibrium and far-from-equilibrium modeling concepts are often combined to describe physical systems. This interdisciplinary book can form the basis of graduate courses in pattern forma- tion and self-assembly. It is a useful reference for graduate students and researchers in a number of disciplines, including condensed matter science, nonequilibrium sta- tistical mechanics, nonlinear dynamics, chemical biophysics, materials science, and engineering. Rashmi C. Desai is Professor Emeritus of Physics at the University of Toronto, Canada. Raymond Kapral is Professor of Chemistry at the University of Toronto, Canada. DYNAMICS OF SELF-ORGANIZED AND SELF-ASSEMBLED STRUCTURES RASHMI C. DESAI AND RAYMOND KAPRAL University of Toronto CAMBRIDGE UNIVERSITY PRESS Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, São Paulo, Delhi, Dubai, Tokyo Cambridge University Press The Edinburgh Building, Cambridge CB2 8RU, UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridge.org/9780521883610 © R.
    [Show full text]