DOCSLIB.ORG

Arm Spiral Antennas

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Arm Spiral Antennas INVESTIGATION OF CYLINDRICALLY-CONFORMED FOUR- ARM SPIRAL ANTENNAS A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Engineering By DOUGLAS JEREMY GLASS B.S.E.P., Wright State University, 2003 2007 Wright State University WRIGHT STATE UNIVERSITY SCHOOL OF GRADUATE STUDIES June 29, 2007 I HEREBY RECOMMEND THAT THE THESIS PREPARED UNDER MY SUPERVISION BY Douglas Jeremy Glass ENTITLED Investigation of Cylindrically- Conformed Four-Arm Spiral Antennas BE ACCEPTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Master of Science in Engineering. _________________________________ Ronald Riechers, Ph.D. Thesis Director _________________________________ Fred Garber, Ph.D. Department Chair Committee on Final Examination _________________________________ Ronald Riechers, Ph.D. _________________________________ Fred Garber, Ph.D. _________________________________ Marian Kazimierczuk, Ph.D. _________________________________ Joseph F. Thomas, Jr., Ph.D. Dean, School of Graduate Studies ABSTRACT Glass, Douglas Jeremy, M.S. Egr., Department of Electrical Engineering, Wright State University, 2007. Investigation of Cylindrically-Conformed Four-Arm Spiral Antennas. A four-arm spiral antenna offers broadband frequency response, wide beamwidths, reduced size compared to other antenna designs, and the ability to determine the relative direction of an incident signal with appropriate mode-forming. The reduced overall area projection of the four-arm spiral antenna compared to other antenna designs and the ability to be manufactured in a planar format allows the antenna to reside within an Unmanned Air Vehicle (UAV) fuselage. This thesis investigates the effects of cylindrically-conforming two different designs of a four-arm spiral antenna to reside within the fuselage of a medium-sized UAV. Theoretical predictions of antenna performance were created using the Numerical Electromagnetics Code (NEC) package and compared to measured results of flat and cylindrically-conformed four-arm spiral antennas with and without ground plane apertures. iii Table of Contents Page 1. Introduction………………………………………………………………..…………1 1.1. Thesis Motivation…………………………………………………………...……1 1.2. Thesis Objectives…………………………………………………………………1 2. Frequency-Independent Antennas……………………………………...…………..2 2.1. Theory of Frequency Independence…………………………………………..….2 2.2. Types of Frequency-Independent Antennas…………………………………...…5 2.2.1. Biconical Antennas……………………………………………………..…5 2.2.2. Log-Periodic Antennas……………………………………............…..…..8 2.2.3. Spiral Antennas……………………………………………………….….12 2.3. Modal Behavior of the Spiral Antenna…………………………………….....…19 3. Antenna System Development……………………………………….….………....26 3.1. Spiral Antenna Development………………………………………………...….26 3.1.1. Spiral Antenna Design……………………………………………...……26 3.1.2. Spiral Antenna Fabrication………………………………………...…….28 3.2. Mode-Former Development…………………………………………………….35 3.2.1. Mode-Former Design ……………………………………………………35 3.2.2. Mode-Former Fabrication ……………………………………………….36 4. Theoretical Model……………………………………………………….……….…39 4.1. Maxwell’s Equations……………………………………………………...…….39 4.2. Numerical Electromagnetics Code Discussion…………………………...……..41 4.2.1. Integral Equations……………………………………………………..…41 4.2.2. Thin Wire Approximation…………………………………………..……44 4.2.3. Method of Moments Solution Method……………………………….…..48 4.3. Numerical Electromagnetics Code Results…………………………………..…54 4.3.1. Archimedean Spiral……………………………………………….……..55 4.3.2. Cylindrically-Conformed Archimedean Spiral………………………..…66 4.3.3. Square Spiral…………………………………………………………..…76 4.3.4. Cylindrically-Conformed Square Spiral……………………………..…..86 4.3.5. Radius of Curvature Analysis of the Archimedean Spiral…………….…96 5. Measured Results…………………………………………………………..…..….102 5.1. Measurement Method………………………………………………………….102 5.1.1. Vector Network Analyzer Discussion………………………………….103 5.1.2. Reference Antenna Discussion…………………………………………104 5.1.3. Desktop Antenna Measurement System Discussion……………………105 5.2. Mode-Former Results………………………………………………………….107 iv 5.2.1. Power Pattern Phase Balance Comparison……………………………..113 5.3. Spiral Antenna Results………………………………………………...………119 5.3.1. Archimedean Spiral……………………………………………...……..120 5.3.2. Cylindrically-Conformed Archimedean Spiral…………………………125 5.3.3. Square Spiral……………………………………………………...…….130 5.3.4. Cylindrically-Conformed Square Spiral………………………………..135 5.3.5. Square Spiral within Ground Plane Aperture……………………….….140 5.3.6. Cylindrically-Conformed Archimedean Spiral within Ground Plane Aperture…………………………………………………………….…..148 6. Conclusions…………………………………………………………….…………..158 6.1. Summary of Work……………………………………………………….…….158 6.2. Recommendations for Further Study…………………………………..………159 References………………………………………………………………..……….........160 v Acknowledgements I would like to begin by thanking Dr. Ronald Riechers for all the time that he has spent guiding and motivating me to complete this task. I would also like to thank Dr. Riechers for instilling a passion for electromagnetics that has only grown over the many years that I have had the honor of being one of his students. I would also like to thank the personnel and the measurement capabilities of Spectral Energetics Incorporated. Without it, I would not have had any measured data with which to compare my theoretical model. I would also like to thank Dr. Fred Garber and the Electrical Engineering Department of Wright State University for providing me the opportunity to attain a Master of Science in Engineering. I would also like to thank Dr. Marian Kazimierczuk for taking the time to serve on my committee. Finally, I would also like to thank Mr. Barry Woods. Without his guidance, my undergraduate and graduate experience would not have been as enjoyable. My final thank you goes out to all my friends and family who encouraged me throughout my education, especially my friend Jason and my oldest brother John. I would also like to thank my friends Mark Stewart, Lamar Westbrook, and Edward Dininger for the time they spent helping me take antenna pattern measurements and my friend Dr. Chad Hagedorn for his time spent editing my thesis. Finally, to my wife Sharon, without your love, patience, and understanding, “Sweets,” none of this would have been possible. vi 1. INTRODUCTION 1.1. Thesis Motivation Developing a low-cost (disposable) and light-weight direction-finding system for use with an Unmanned Air Vehicle (UAV) is the motivation of this thesis. As the battlefield evolves around the world, the ability to locate communications of enemy combatants is one of the most relevant tasks for supporting the war-fighter. Developing an antenna for a direction-finding system with an emphasis on modularity for different mission types and broad frequency response would demonstrate the utility of such a system to the military. 1.2. Thesis Objectives The objectives of this thesis are the following: Define a suitable antenna as defined by the thesis motivation. Describe the characteristics of the antenna. Discuss the development of an antenna capable of direction-finding. Define a theoretical model capable of describing the antenna. Provide a comparison of the theoretical and measured results. 1 2. FREQUENCY-INDEPENDENT ANTENNAS 2.1 Theory of Frequency Independence Due to the ever-expanding utilization of the electromagnetic spectrum, antennas that can operate over wide frequency ranges have become increasingly desirable. As stated in Balanis [1], prior to the 1950s, antenna technology could only provide bandwidths of 2:1 or less. Afterwards though, the concept of specifying antenna geometries purely by angles instead of characteristic lengths allowed for bandwidths of 40:1 or more. If an antenna is only defined by angles, attributes such as the characteristic input impedance, field pattern, and polarization remain constant as the size of the antenna is scaled. The theory of frequency-independence, as described by the work of Rumsey [2] and Elliot [3], begins by assuming an antenna geometry within spherical coordinates (ρ,θ,φ ), where each terminal (feed point) of the antenna surface is infinitesimally close to the origin and is confined to rotation about the θ = 0 axis. To further simplify the problem, surfaces are assumed to be perfectly conducting, and the region surrounding the antenna is assumed to be infinite in extent, homogenous, and isotropic. Such a surface is described by a single curve (for a wire) or a set of curves (to define the edges of a strip) r = F(θ,φ) (2.1-1) 2 where r represents the radial distance along the curve. To define the property of scaling, start by assuming an antenna were to be scaled to operate at a frequency that is K times lower than the original antenna. The physical size of the antenna would need to be increased by a factor of K. The scaled curve is then described by r′ = KF(θ,φ) (2.1-2) where both surfaces superimpose one another after the second curve is rotated by an angle φc about the θ = 0 axis. This is shown by the following F(θ,φ +φc ) = KF(θ,φ) (2.1-3) where the rotated angle φc depends only on K. The following figure depicts three spirals that correspond to a single-arm spiral, a scaled single-arm spiral, and a scaled single-arm spiral that has been rotated to visualize congruence of the two spirals. Figure 2.1-1 Comparison of Scaled Spirals 3 To prove congruence between the two curves, begin by differentiating both sides of equation (2.1-3) with respect to both φc and φ. d dK ∂ []KF()θ,φ = []F()θ,φ = []F()θ,φ +φc (2.1-4) dφc dφc ∂φc d ∂ []KF()θ,φ
Load more

Recommended publications
  • The Ordered Distribution of Natural Numbers on the Square Root Spiral
    The Ordered Distribution of Natural Numbers on the Square Root Spiral - Harry K. Hahn - Ludwig-Erhard-Str. 10 D-76275 Et Germanytlingen, Germany ------------------------------ mathematical analysis by - Kay Schoenberger - Humboldt-University Berlin ----------------------------- 20. June 2007 Abstract : Natural numbers divisible by the same prime factor lie on defined spiral graphs which are running through the “Square Root Spiral“ ( also named as “Spiral of Theodorus” or “Wurzel Spirale“ or “Einstein Spiral” ). Prime Numbers also clearly accumulate on such spiral graphs. And the square numbers 4, 9, 16, 25, 36 … form a highly three-symmetrical system of three spiral graphs, which divide the square-root-spiral into three equal areas. A mathematical analysis shows that these spiral graphs are defined by quadratic polynomials. The Square Root Spiral is a geometrical structure which is based on the three basic constants: 1, sqrt2 and π (pi) , and the continuous application of the Pythagorean Theorem of the right angled triangle. Fibonacci number sequences also play a part in the structure of the Square Root Spiral. Fibonacci Numbers divide the Square Root Spiral into areas and angle sectors with constant proportions. These proportions are linked to the “golden mean” ( golden section ), which behaves as a self-avoiding-walk- constant in the lattice-like structure of the square root spiral. Contents of the general section Page 1 Introduction to the Square Root Spiral 2 2 Mathematical description of the Square Root Spiral 4 3 The distribution
    [Show full text]
  • Some Curves and the Lengths of Their Arcs Amelia Carolina Sparavigna
    Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna To cite this version: Amelia Carolina Sparavigna. Some Curves and the Lengths of their Arcs. 2021. hal-03236909 HAL Id: hal-03236909 https://hal.archives-ouvertes.fr/hal-03236909 Preprint submitted on 26 May 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna Department of Applied Science and Technology Politecnico di Torino Here we consider some problems from the Finkel's solution book, concerning the length of curves. The curves are Cissoid of Diocles, Conchoid of Nicomedes, Lemniscate of Bernoulli, Versiera of Agnesi, Limaçon, Quadratrix, Spiral of Archimedes, Reciprocal or Hyperbolic spiral, the Lituus, Logarithmic spiral, Curve of Pursuit, a curve on the cone and the Loxodrome. The Versiera will be discussed in detail and the link of its name to the Versine function. Torino, 2 May 2021, DOI: 10.5281/zenodo.4732881 Here we consider some of the problems propose in the Finkel's solution book, having the full title: A mathematical solution book containing systematic solutions of many of the most difficult problems, Taken from the Leading Authors on Arithmetic and Algebra, Many Problems and Solutions from Geometry, Trigonometry and Calculus, Many Problems and Solutions from the Leading Mathematical Journals of the United States, and Many Original Problems and Solutions.
    [Show full text]
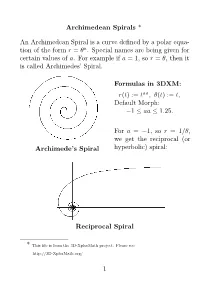
  • Archimedean Spirals ∗
    Archimedean Spirals ∗ An Archimedean Spiral is a curve defined by a polar equation of the form r = θa, with special names being given for certain values of a. For example if a = 1, so r = θ, then it is called Archimedes’ Spiral. Archimede’s Spiral For a = −1, so r = 1/θ, we get the reciprocal (or hyperbolic) spiral. Reciprocal Spiral ∗This file is from the 3D-XploreMath project. You can find it on the web by searching the name. 1 √ The case a = 1/2, so r = θ, is called the Fermat (or hyperbolic) spiral. Fermat’s Spiral √ While a = −1/2, or r = 1/ θ, it is called the Lituus. Lituus In 3D-XplorMath, you can change the parameter a by going to the menu Settings → Set Parameters, and change the value of aa. You can see an animation of Archimedean spirals where the exponent a varies gradually, from the menu Animate → Morph. 2 The reason that the parabolic spiral and the hyperbolic spiral are so named is that their equations in polar coordinates, rθ = 1 and r2 = θ, respectively resembles the equations for a hyperbola (xy = 1) and parabola (x2 = y) in rectangular coordinates. The hyperbolic spiral is also called reciprocal spiral because it is the inverse curve of Archimedes’ spiral, with inversion center at the origin. The inversion curve of any Archimedean spirals with respect to a circle as center is another Archimedean spiral, scaled by the square of the radius of the circle. This is easily seen as follows. If a point P in the plane has polar coordinates (r, θ), then under inversion in the circle of radius b centered at the origin, it gets mapped to the point P 0 with polar coordinates (b2/r, θ), so that points having polar coordinates (ta, θ) are mapped to points having polar coordinates (b2t−a, θ).
    [Show full text]
  • Analysis of Spiral Curves in Traditional Cultures
    Forum _______________________________________________________________ Forma, 22, 133–139, 2007 Analysis of Spiral Curves in Traditional Cultures Ryuji TAKAKI1 and Nobutaka UEDA2 1Kobe Design University, Nishi-ku, Kobe, Hyogo 651-2196, Japan 2Hiroshima-Gakuin, Nishi-ku, Hiroshima, Hiroshima 733-0875, Japan *E-mail address: [email protected] *E-mail address: [email protected] (Received November 3, 2006; Accepted August 10, 2007) Keywords: Spiral, Curvature, Logarithmic Spiral, Archimedean Spiral, Vortex Abstract. A method is proposed to characterize and classify shapes of plane spirals, and it is applied to some spiral patterns from historical monuments and vortices observed in an experiment. The method is based on a relation between the length variable along a curve and the radius of its local curvature. Examples treated in this paper seem to be classified into four types, i.e. those of the Archimedean spiral, the logarithmic spiral, the elliptic vortex and the hyperbolic spiral. 1. Introduction Spiral patterns are seen in many cultures in the world from ancient ages. They give us a strong impression and remind us of energy of the nature. Human beings have been familiar to natural phenomena and natural objects with spiral motions or spiral shapes, such as swirling water flows, swirling winds, winding stems of vines and winding snakes. It is easy to imagine that powerfulness of these phenomena and objects gave people a motivation to design spiral shapes in monuments, patterns of cloths and crafts after spiral shapes observed in their daily lives. Therefore, it would be reasonable to expect that spiral patterns in different cultures have the same geometrical properties, or at least are classified into a small number of common types.
    [Show full text]
  • Superconics + Spirals 17 July 2017 1 Superconics + Spirals Cye H
    Superconics + Spirals 17 July 2017 Superconics + Spirals Cye H. Waldman Copyright 2017 Introduction Many spirals are based on the simple circle, although modulated by a variable radius. We have generalized the concept by allowing the circle to be replaced by any closed curve that is topologically equivalent to it. In this note we focus on the superconics for the reasons that they are at once abundant, analytical, and aesthetically pleasing. We also demonstrate how it can be applied to random closed forms. The spirals of interest are of the general form . A partial list of these spirals is given in the table below: Spiral Remarks Logarithmic b = flair coefficient m = 1, Archimedes Archimedean m = 2, Fermat (generalized) m = -1, Hyperbolic m = -2, Lituus Parabolic Cochleoid Poinsot Genesis of the superspiral (1) The idea began when someone on line was seeking to create a 3D spiral with a racetrack planiform. Our first thought was that the circle readily transforms to an ellipse, for example Not quite a racetrack, but on the right track. The rest cascades in a hurry, as This is subject to the provisions that the random form is closed and has no crossing lines. This also brought to mind Euler’s famous derivation, connecting the five most famous symbols in mathematics. 1 Superconics + Spirals 17 July 2017 In the present paper we’re concerned primarily with the superconics because the mapping is well known and analytic. More information on superconics can be found in Waldman (2016) and submitted for publication by Waldman, Chyau, & Gray (2017). Thus, we take where is a parametric variable (not to be confused with the polar or tangential angles).
    [Show full text]
  • Archimedean Spirals * an Archimedean Spiral Is a Curve
    Archimedean Spirals * An Archimedean Spiral is a curve defined by a polar equa- tion of the form r = θa. Special names are being given for certain values of a. For example if a = 1, so r = θ, then it is called Archimedes’ Spiral. Formulas in 3DXM: r(t) := taa, θ(t) := t, Default Morph: 1 aa 1.25. − ≤ ≤ For a = 1, so r = 1/θ, we get the− reciprocal (or Archimede’s Spiral hyperbolic) spiral: Reciprocal Spiral * This file is from the 3D-XplorMath project. Please see: http://3D-XplorMath.org/ 1 The case a = 1/2, so r = √θ, is called the Fermat (or hyperbolic) spiral. Fermat’s Spiral While a = 1/2, or r = 1/√θ, it is called the Lituus: − Lituus 2 In 3D-XplorMath, you can change the parameter a by go- ing to the menu Settings Set Parameters, and change the value of aa. You can see→an animation of Archimedean spirals where the exponent a = aa varies gradually, be- tween 1 and 1.25. See the Animate Menu, entry Morph. − The reason that the parabolic spiral and the hyperbolic spiral are so named is that their equations in polar coor- dinates, rθ = 1 and r2 = θ, respectively resembles the equations for a hyperbola (xy = 1) and parabola (x2 = y) in rectangular coordinates. The hyperbolic spiral is also called reciprocal spiral be- cause it is the inverse curve of Archimedes’ spiral, with inversion center at the origin. The inversion curve of any Archimedean spirals with re- spect to a circle as center is another Archimedean spiral, scaled by the square of the radius of the circle.
    [Show full text]
  • APS March Meeting 2012 Boston, Massachusetts
    APS March Meeting 2012 Boston, Massachusetts http://www.aps.org/meetings/march/index.cfm i Monday, February 27, 2012 8:00AM - 11:00AM — Session A51 DCMP DFD: Colloids I: Beyond Hard Spheres Boston Convention Center 154 8:00AM A51.00001 Photonic Droplets Containing Transparent Aqueous Colloidal Suspensions with Optimal Scattering Properties JIN-GYU PARK, SOFIA MAGKIRIADOU, Department of Physics, Harvard University, YOUNG- SEOK KIM, Korea Electronics Technology Institute, VINOTHAN MANOHARAN, Department of Physics, Harvard University, HARVARD UNIVERSITY TEAM, KOREA ELECTRONICS TECHNOLOGY INSTITUTE COLLABORATION — In recent years, there has been a growing interest in quasi-ordered structures that generate non-iridescent colors. Such structures have only short-range order and are isotropic, making colors invariant with viewing angle under natural lighting conditions. Our recent simulation suggests that colloidal particles with independently controlled diameter and scattering cross section can realize the structural colors with angular independence. In this presentation, we are exploiting depletion-induced assembly of colloidal particles to create isotropic structures in a milimeter-scale droplet. As a model colloidal particle, we have designed and synthesized core-shell particles with a large, low refractive index shell and a small, high refractive index core. The remarkable feature of these particles is that the total cross section for the entire core-shell particle is nearly the same as that of the core particle alone. By varying the characteristic length scales of the sub-units of such ‘photonic’ droplet we aim to tune wavelength selectivity and enhance color contrast and viewing angle. 8:12AM A51.00002 Curvature-Induced Capillary Interaction between Spherical Particles at a Liquid Interface1 , NESRIN SENBIL, CHUAN ZENG, BENNY DAVIDOVITCH, ANTHONY D.
    [Show full text]
  • Dynamics of Self-Organized and Self-Assembled Structures
    This page intentionally left blank DYNAMICS OF SELF-ORGANIZED AND SELF-ASSEMBLED STRUCTURES Physical and biological systems driven out of equilibrium may spontaneously evolve to form spatial structures. In some systems molecular constituents may self-assemble to produce complex ordered structures. This book describes how such pattern formation processes occur and how they can be modeled. Experimental observations are used to introduce the diverse systems and phenom- ena leading to pattern formation. The physical origins of various spatial structures are discussed, and models for their formation are constructed. In contrast to many treatments, pattern-forming processes in nonequilibrium systems are treated in a coherent fashion. The book shows how near-equilibrium and far-from-equilibrium modeling concepts are often combined to describe physical systems. This interdisciplinary book can form the basis of graduate courses in pattern forma- tion and self-assembly. It is a useful reference for graduate students and researchers in a number of disciplines, including condensed matter science, nonequilibrium sta- tistical mechanics, nonlinear dynamics, chemical biophysics, materials science, and engineering. Rashmi C. Desai is Professor Emeritus of Physics at the University of Toronto, Canada. Raymond Kapral is Professor of Chemistry at the University of Toronto, Canada. DYNAMICS OF SELF-ORGANIZED AND SELF-ASSEMBLED STRUCTURES RASHMI C. DESAI AND RAYMOND KAPRAL University of Toronto CAMBRIDGE UNIVERSITY PRESS Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, São Paulo, Delhi, Dubai, Tokyo Cambridge University Press The Edinburgh Building, Cambridge CB2 8RU, UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridge.org/9780521883610 © R.
    [Show full text]
  • John Sharp Spirals and the Golden Section
    John Sharp Spirals and the Golden Section The author examines different types of spirals and their relationships to the Golden Section in order to provide the necessary background so that logic rather than intuition can be followed, correct value judgments be made, and new ideas can be developed. Introduction The Golden Section is a fascinating topic that continually generates new ideas. It also has a status that leads many people to assume its presence when it has no relation to a problem. It often forces a blindness to other alternatives when intuition is followed rather than logic. Mathematical inexperience may also be a cause of some of these problems. In the following, my aim is to fill in some gaps, so that correct value judgements may be made and to show how new ideas can be developed on the rich subject area of spirals and the Golden Section. Since this special issue of the NNJ is concerned with the Golden Section, I am not describing its properties unless appropriate. I shall use the symbol I to denote the Golden Section (I |1.61803 ). There are many aspects to Golden Section spirals, and much more could be written. The parts of this paper are meant to be read sequentially, and it is especially important to understand the different types of spirals in order that the following parts are seen in context. Part 1. Types of Spirals In order to understand different types of Golden Section spirals, it is necessary to be aware of the properties of different types of spirals. This section looks at spirals from that viewpoint.
    [Show full text]
  • Curves Defined Using Polar Coordinates
    Curves defined using polar coordinates Instead of using Cartesian (x; y) coordinates, we can describe points in the plane by specifying how far they are from some fixed reference point (the pole) and the angle the line from the point to the pole makes with some reference direction. The convention is to treat the origin (0; 0) as the pole, and the reference direction as the positive x-axis. In this way, we can convert back and forth between polar coordinates and cartesian. So a point in the plane may be specified by a pair (r; θ) like this: (r; θ) r θ Here are some points in both xy-coordinates and polar coordinates: Cartesian polar (1; 0) (p1; 0) (1; 1) ( 2; π p 4 (0; 1) (1; π2 (−1; 0) (p1; π) 5π (−1; −1 ( 2; 4 3π (0; −1) (1; 2 (3; 7) (7:6157:::; 1:1659:::) (0:5673:::; −1:9178) (2; 5) To convert back and forth, we can use these relationships: x = r cos θ; y = r sin θ and p y r = x 2 + y 2; θ = tan−1 x with the caveat that the theta value yielded might be negative. For example, (r; θ); (−r; θ + π); (−r; θ + 3π); (r; θ + 2π) all represent the same point. This makes thing interesting: simple polar equations can create complex curves. Which brings us the main oddity of polar coordinates: they are not unique. If we add 2π (or any multiple of 2 pi) to θ, we are specifying the same point. We can even use a negative r if we add an odd multiple π to θ.
    [Show full text]
  • The Mathematics and Art of Spirals Workshop
    Proceedings of Bridges 2013: Mathematics, Music, Art, Architecture, Culture The Mathematics and Art of Spirals Workshop Ann Hanson Science and Mathematics Department, Columbia College Chicago, 600 S. Michigan, Chicago, IL 606005 [email protected] Abstract In this workshop, the participants will learn several properties of spirals. Some of the properties are: that all spirals start from a fixed point and move out from that point in a regular manner. Other universal properties of spirals and their mathematical connections will be demonstrated by making an Archimedean spiral, a Golden spiral and a Baravelle spiral. The presenter will supply all equipment needed for the activities. A spiral is a curve that moves out from the center in a regular manner getting progressively farther away as it moves out. The spiral shape is so prevalent that it is easy not to notice them. They can be seen in natural objects, such as in the shells of mollusks, sunflower heads and in vortices in air and water. Spirals are also seen in the coil of watch balance springs, the grooves of a phonograph record and in the roll of paper towels. In addition, all spirals have some common characteristics. They all have a fixed starting point (center) and move out from the center in a regular manner. Spirals grow by self-accumulation and solve a problem of efficient growth in terms of energy, materials and expansion within space. The previously mentioned properties as well as other mathematical properties will be examined and demonstrated through hands-on activities. For example, the participants will make a one type of spiral called an Archimedean spiral using polar graph paper.
    [Show full text]
  • Collected Atos
    Mathematical Documentation of the objects realized in the visualization program 3D-XplorMath Select the Table Of Contents (TOC) of the desired kind of objects: Table Of Contents of Planar Curves Table Of Contents of Space Curves Surface Organisation Go To Platonics Table of Contents of Conformal Maps Table Of Contents of Fractals ODEs Table Of Contents of Lattice Models Table Of Contents of Soliton Traveling Waves Shepard Tones Homepage of 3D-XPlorMath (3DXM): http://3d-xplormath.org/ Tutorial movies for using 3DXM: http://3d-xplormath.org/Movies/index.html Version November 29, 2020 The Surfaces Are Organized According To their Construction Surfaces may appear under several headings: The Catenoid is an explicitly parametrized, minimal sur- face of revolution. Go To Page 1 Curvature Properties of Surfaces Surfaces of Revolution The Unduloid, a Surface of Constant Mean Curvature Sphere, with Stereographic and Archimedes' Projections TOC of Explicitly Parametrized and Implicit Surfaces Menu of Nonorientable Surfaces in previous collection Menu of Implicit Surfaces in previous collection TOC of Spherical Surfaces (K = 1) TOC of Pseudospherical Surfaces (K = −1) TOC of Minimal Surfaces (H = 0) Ward Solitons Anand-Ward Solitons Voxel Clouds of Electron Densities of Hydrogen Go To Page 1 Planar Curves Go To Page 1 (Click the Names) Circle Ellipse Parabola Hyperbola Conic Sections Kepler Orbits, explaining 1=r-Potential Nephroid of Freeth Sine Curve Pendulum ODE Function Lissajous Plane Curve Catenary Convex Curves from Support Function Tractrix
    [Show full text]