Modelling the Optimum Interface Between Open Pit and Underground Mining for Gold Mines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Arend J Hoogervorst1 B.Sc.(Hons), Mphil., Pr.Sci
Audits & Training Eagle Environmental Arend J Hoogervorst1 B.Sc.(Hons), MPhil., Pr.Sci. Nat., MIEnvSci., C.Env., MIWM Environmental Audits Undertaken, Lectures given, and Training Courses Presented2 A) AUDITS UNDERTAKEN (1991 – Present) (Summary statistics at end of section.) Key ECA - Environmental Compliance Audit EMA - Environmental Management Audit EDDA -Environmental Due Diligence Audit EA- External or Supplier Audit or Verification Audit HSEC – Health, Safety, Environment & Community Audit (SHE) – denotes safety and occupational health issues also dealt with * denotes AJH was lead environmental auditor # denotes AJH was contracted specialist local environmental auditor for overseas environmental consultancy, auditing firm or client + denotes work undertaken as an ICMI-accredited Lead Auditor (Cyanide Code) No of days shown indicates number of actual days on site for audit. [number] denotes number of days involved in audit preparation and report write up. 1991 *2 day [4] ECA - AECI Chlor-Alkali Plastics, Umbogintwini, KwaZulu-Natal, South Africa. November 1991. *2 day [4] ECA - AECI Chlor-Alkali Plastics- Environmental Services, Umbogintwini, KwaZulu-Natal, South Africa. November 1991. *2 Day [4] ECA - Soda Ash Botswana, Sua Pan, Botswana. November 1991. 1992 *2 Day [4] EA - Waste-tech Margolis, hazardous landfill site, Gauteng, South Africa. February 1992. *2 Day [4] EA - Thor Chemicals Mercury Reprocessing Plant, Cato Ridge, KwaZulu-Natal, South Africa. March 1992. 2 Day [4] EMA - AECI Explosives Plant, Modderfontein, Gauteng, South Africa. March 1992. *2 Day [4] EMA - Anikem Water Treatment Chemicals, Umbogintwini, KwaZulu-Natal, South Africa. March 1992. *2 Day [4] EMA - AECI Chlor-Alkali Plastics Operations Services Group, Midland Factory, Sasolburg. March 1992. *2 Day [4] EMA - SA Tioxide factory, Umbogintwini, KwaZulu-Natal, South Africa. -

Minesafe Magazine for More Information on the Harmonisation Process
minesafeWESTERN AUSTRALIA Volume 20 no. 3 DECEMBER 2011 Conveyors – guarding against inadequacy TOOLS TO HANDLE WORKPLACE OSH ISSUES FEEDBACK SOUGHT ON DRILLING CODE OF PRACTICE MINES SAFETY PRIORITIES FOR THE REGULATOR 07 04 22 17 19 CONTENTS DEPARTMENTAL NEWS OCCUPATIONAL HEALTH 2011 SOUTH WEST CRUNCHING THE NUMBERS 02 Harmonisation of 13 More to CONTAM than EMERGENCY RESPONSE 51 Distribution of safety and occupational health and meeting quotas SKILLS CHALLENGE health representatives as safety laws 26 Taking up the challenge at 30 September 2011 DANGEROUS GOODS 03 Comment sought for MIAC 28 Motley crew gets the job 52 Monthly exploration SAFETY review done workforce to September 14 Report missing explosives 2011 DIVISIONAL NEWS 30 First aid scenario in tempo 15 Is your explosives or SRS with drum warnings 53 Monthly mining workforce to September 2011 04 Regulators meet in Darwin licence still valid? 32 Beau puts his body and 06 Resources Safety hosts 16 Shotfiring training – new mind on the line SIGNIFICANT INCIDENT PM’s 2011 Pacific Award competencies Recipient 2011 UNDERGROUND REPORTS AND SAFETY BULLETINS 07 Roadshows increase INDUSTRY ACTIVITIES MINE EMERGENCY opportunities for 17 Mines safety priorities for RESPONSE COMPETITION 54 Mines Safety SIR 173 consultation Employee burnt while the regulator 40 Sunrise Dam continues setting up scenario for winning trend SIMON SAYS 18 MARK YOUR DIARY emergency response 42 Universal language of training 09 2011 was a momentous mine rescue year of change SAFETY ALERTS AND 55 Mines Safety Bulletin -

Ore Genesis and Modelling of the Sadiola Hill Gold Mine, Mali Geology Honours Project
ORE GENESIS AND MODELLING OF THE SADIOLA HILL GOLD MINE, MALI GEOLOGY HONOURS PROJECT Ramabulana Tshifularo Student number: 462480 Supervisor: Prof Kim A.A. Hein Acknowledgements I would like to thank my supervisor, Prof. Kim Hein for giving me the opportunity to be part of her team and, for helping and motivating me during the course of the project. Thanks for your patience, constructive comments and encouragement. Thanks to my family and my friends for the encouragements and support. Table of contents Abstract……………………………………………………………………………………..i Chapter: 1 1.1 Introduction……………………………………………………..........................................1 1.2 Location and Physiography……………………………………………………………...2 1.3 Aims and Objectives…………………………………………………………………….3 1.4 Abbreviations and acronyms…………………………………………………………….3 Chapter 2 2.1 Regional Geology………………………………………………………………………..4 2.1.1 Geology of the West African Craton…………………………………………………..4 2.1.2 Geology of the Kedougou-Kéniéba Inlier……………………………………………..5 2.2 Mine geology…………………………………………………………………………….6 Lithology………………………………………………………………………………8 Structure……………………………………………………………………………….8 Metamorphism………………………………………………………………………...9 Gold mineralisation and metallogenesis………………………………………………9 2.4 Previously suggested genetic models…………………………………………………..10 Chapter3: Methodology…………………………………………………………………....11 Chapter 4: Host rocks in drill core…......................................................................................13 4.1 Drill core description….........................................................................................................13 -

Anglogold Ashanti Geita Gold Mine Expression of Interest/Request for Information Provision of Underground Mechanized Contract Mi
ANGLOGOLD ASHANTI GEITA GOLD MINE EXPRESSION OF INTEREST/REQUEST FOR INFORMATION PROVISION OF UNDERGROUND MECHANIZED CONTRACT MINING SERVICES AT GEITA GOLD MINE TANZANIA INTRODUCTION Geita Gold Mining Limited and Anglo Gold Ashati Ltd is subsidiary is located in north western Tanzania in Lake Victoria goldfields of geita about 120 KM from Mwanza and 44 KM West of the town of geita Town The purpose of EO is to explore the supply market for competent providers with the requisite technical skills and knowledge and financial capacity to undertake the Supply and Delivery of Capital projects Goods and Service to Geita Gold Mine in accordance with the tender document The response of this EOI will be used to shortlist capable service provider that will be invited to respond to the main tender for provision of various works/service for Geita Gold mining Ltd. The details and date for the issues of the main tender will be communicated to shortlisted companies only. It is necessary to respond to EOI/RFI in order to be pre-qualified be considered for the main tender SCOPE OF WORK Provision of Services as detailed below S/N Reference Projects Description No 1 GGME0955 Provision of Underground Mechanized contract mining services for Geita Gold Mining Ltd SCOPE The EOI for the supply of underground mechanized contract mining services is for two UG mines in the GGM complex Nyakanga Ug Geita Hill UG the Nyakanga and Geita Hill orebodies will be mined using mechanized mining method development will ultilized standard Jumbo drilling and bolting for ground support, while any production activity will be based around a variation of long hole one stopping. -
Year End 2020
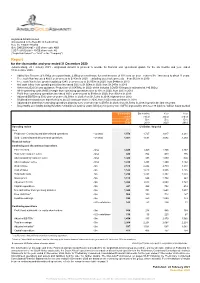
AngloGold Ashanti Limited (Incorporated in the Republic of South Africa) Reg. No. 1944/017354/06 ISIN: ZAE000043485 – JSE share code: ANG CUSIP: 035128206 – NYSE share code: AU (“AngloGold Ashanti” or “AGA” or the “Company”) Report for the six months and year ended 31 December 2020 Johannesburg, 22 February 2021 - AngloGold Ashanti is pleased to provide its financial and operational update for the six months and year ended 31 December 2020. • Added Ore Reserve of 6.1Moz on a gross basis, 2.6Moz on a net basis, for a net increase of 10% year-on-year - reserve life ∧ increased to about 11 years • Free cash flow increased 485% year-on-year to $743m in 2020 – excluding asset sale proceeds – from $127m in 2019 • Free cash flow before growth capital up 124% year-on-year to $1,003m in 2020, from $448m in 2019 • Net cash inflow from operating activities increased 58% to $1,654m in 2020, from $1,047m in 2019 • Achieved 2020 full year guidance: Production of 3.047Moz in 2020, which includes COVID-19 impacts estimated at 140,000oz • All-in sustaining costs (AISC) margin from continuing operations rose to 40% in 2020, from 28% in 2019 • Profit from continuing operations increased 160% year-on-year to $946m in 2020, from $364m in 2019 • Adjusted EBITDA up 50% year-on-year to $2,593m in 2020, from $1,723m in 2019; highest since 2012 • Dividend increased more than fivefold to 48 US cents per share in 2020, from 9 US cents per share in 2019 • Adjusted net debt from continuing operations down by 62% year-on-year to $597m in 2020, from $1,581m in 2019; -

PDF.Js Viewer
Exploration and Innovation The Discovery and Evolution of the 2Moz Vogue Gold Resource, Sunrise Dam Gold Mine, Western Australia M Nugus1,2, N Oliver3, T G Blenkinsop4, J Hill5, J G McLellan6, JCleverley5, L Fisher5, N Brunacci7, H Moore8 and A Jenkins9 ABSTRACT The 2 Moz Vogue mineral resource is a recent discovery at the Sunrise Dam gold mine (SDGM), lying approximately 600 m vertically below the Sunrise Dam open pit. Unlike most other lodes, which are dominated either by steep vein sets or shallow high-strain (shear) zones, it lies broadly in the hinge of a folded felsic porphyry body, where it cuts intermediate volcanic lavas and volcaniclastic rocks and is not speciÀcally concentrated at a lithofacies contact. The mineralisation is controlled by a complex interplay of moderate to shallow, west-dipping high-strain zones that are transected by irregular and discontinuous high-grade, north-west-, north–south- and east– west-trending breccia sheets that initially caused problems with attempts to model broad domains. However, by combining the structural controls and styles with the distribution of gold, arsenic, sulfur and antimony, we have improved opportunities for scheduling, extracting and processing the most appropriate material considering the current mining and processing constraints. The early delineation process for the Vogue lode revealed a signiÀcant mineral resource for the SDGM, coupled with the recognition of some potentially difÀcult downstream implications for mining and processing. The ultimate success of mining at Vogue will be a consequence of combining standardised data collection and geological modelling techniques with the results of the novel innovative techniques applied at an early stage of the project. -

Anglogold Ashanti Holdings Plc Anglogold Ashanti Limited
Use these links to rapidly review the document TABLE OF CONTENTS Prospectus Supplement TABLE OF CONTENTS TABLE OF CONTENTS 3 Table of Contents Filed pursuant to Rule 424(b)(5) Registration Nos. 333-182712 and 333-182712-02 CALCULATION OF REGISTRATION FEE Amount of Registration Title of Each Class of Aggregate Securities to be Registered Offering Price Fee (1) 5.125% Notes due 2022 of AngloGold Ashanti Holdings plc $750,000,000 $85,950 Guarantee of AngloGold Ashanti Limited in connection with the 5.125% Notes due 2022 (2) — — (1) Calculated in accordance with Rule 457(r) under the Securities Act of 1933. (2) Pursuant to Rule 457(n) under the Securities Act of 1933, no separate fee is payable with respect to the guarantee of AngloGold Ashanti Limited in connection with the guaranteed debt securities. Prospectus Supplement to Prospectus dated July 17, 2012 GRAPHIC AngloGold Ashanti Holdings plc $750,000,000 5.125% notes due 2022 Fully and Unconditionally Guaranteed by AngloGold Ashanti Limited The 5.125% notes due 2022, or the "notes", will bear interest at a rate of 5.125% per year. AngloGold Ashanti Holdings plc, or "Holdings", will pay interest on the notes each February 1 and August 1, commencing on February 1, 2013. Unless Holdings redeems the notes earlier, the notes will mature on August 1, 2022. The notes will rank equally with Holdings' senior, unsecured debt obligations and the guarantee will rank equally with all other senior, unsecured debt obligations of AngloGold Ashanti Limited. Holdings may redeem some or all of the notes at any time and from time to time at the redemption price determined in the manner described in this prospectus supplement. -

Golden Rules Making the Case for Responsible Mining
GOLDEN RULES Making the case for responsible mining A REPORT BY EARTHWORKS AND OXFAM AMERICA Contents Introduction: The Golden Rules 2 Grasberg Mine, Indonesia 5 Yanacocha Mine, Peru, and Cortez Mine, Nevada 7 BHP Billiton Iron Ore Mines, Australia 9 Hemlo Camp Mines, Canada 10 Mongbwalu Mine, the Democratic Republic of Congo 13 Rosia Montana Mine, Romania 15 Marcopper Mine, the Philippines, and Minahasa Raya and Batu Hijau Mines, Indonesia 17 Porgera Gold Mine, Papua New Guinea 18 Junín Mine, Ecuador 21 Akyem Mine, Ghana 22 Pebble Mine, Alaska 23 Zortman-Landusky Mine, Montana 25 Bogoso/Prestea Mine, Ghana 26 Jerritt Canyon Mine, Nevada 27 Summitville Mine, Colorado 29 Following the rules: An agenda for action 30 Notes 31 Cover: Sadiola Gold Mine, Mali | Brett Eloff/Oxfam America Copyright © EARTHWORKS, Oxfam America, 2007. Reproduction is permitted for educational or noncommercial purposes, provided credit is given to EARTHWORKS and Oxfam America. Around the world, large-scale metals mining takes an enormous toll on the health of the environment and communities. Gold mining, in particular, is one of the dirtiest industries in the world. Massive open-pit mines, some measuring as much as two miles (3.2 kilometers) across, generate staggering quantities of waste—an average of 76 tons for every ounce of gold.1 In the US, metals mining is the leading contributor of toxic emissions to the environment.2 And in countries such as Ghana, Romania, and the Philippines, mining has also been associated with human rights violations, the displacement of people from their homes, and the disruption of traditional livelihoods. -

Anglogold Ashanti Geita Gold Mine Expression of Interest
ANGLOGOLD ASHANTI GEITA GOLD MINE EXPRESSION OF INTEREST/REQUEST FOR INFORMATION SURFACE EXPLORATION AND GRADE CONTROL DRILLING SERVICES FOR ANGLOGOLD ASHATI GEITA GOLD MINING LIMITED INTRODUCTION Geita Gold Mining Limited and AngloGlod Ashati Ltd is subsidiary is located in north western Tanzania in Lake Victoria goldfields of geita about 120 KM from Mwanza and 44 KM West of the town of geita Anglogold ashant limited has globally diverse world class portfolio of operation projects. AGA is rd the 3 largest mining gold company in the world measured by production, it has 14 gold mine in 9 counties, our exploration programme is aimed at establishing an organic growth pipeline to enable us to generate significant value over time, Greenfields and Brownfield’s exploration is conducted in both establishment and new gold producing regions through managed and non-managed joint venture strategic alliance and wholly owned ground holdings The purpose of EO is to explore the drilling market for competent services provider with the requisite technical skills and financial capacity to undertake exploration and grade conduction control drilling services at our Geita Gold Mine in accordance with the RFI Documents The response of this EOI will be used to shortlist capable service provider that will be invited to respond to the main tender for provision of various works/service for Geita Gold mining Ltd. The details and date for the issues of the main tender will be communicated to shortlisted companies only. It is necessary to respond to EOI/RFI in order to be pre-qualified be considered for the main tender Scope of work The surface exploration and grade control drilling services 1. -

Water Pluto Project Port Study
WESTERN AUSTRALIA’S INTERNATIONAL RESOURCES DEVELOPMENT MAGAZINE March–May 2007 $3 (inc GST) Print post approved PP 665002/00062 approved Print post WATER The potential impact of climate change and lower rainfall on the resources sector PLUTO PROJECT Site works begin on the first new LNG project in WA for 25 years PORT STUDY Ronsard Island recommended as the site for a new Pilbara iron ore port DEPARTMENT OF INDUSTRY AND RESOURCES Investment Services 1 Adelaide Terrace East Perth • Western Australia 6004 Tel: +61 8 9222 3333 • Fax: +61 8 9222 3862 Email: [email protected] www.doir.wa.gov.au INTERNATIONAL OFFICES Europe European Office • 5th floor, Australia Centre Corner of Strand and Melbourne Place London WC2B 4LG • UNITED KINGDOM Tel: +44 20 7240 2881 • Fax: +44 20 7240 6637 Email: [email protected] India — Mumbai Western Australian Trade Office 93 Jolly Maker Chambers No 2 9th floor, Nariman Point • Mumbai 400 021 • INDIA Tel: +91 22 6630 3973 • Fax: +91 22 6630 3977 Email: [email protected] India — Chennai Western Australian Trade Office - Advisory Office 1 Doshi Regency • 876 Poonamallee High Road From the Director General Kilpauk • Chennai 600 084 • INDIA Tel: +91 44 2640 0407 • Fax: +91 44 2643 0064 Email: [email protected] Indonesia — Jakarta Western Australia Trade Office A climate for opportunities and change JI H R Rasuna Said Kav - Kuningan Jakarta 12940 • INDONESIA Tel: +62 21 5290 2860 • Fax: +62 21 5296 2722 Many experts and analysts are forecasting that 2007 will bring exciting new Email: [email protected] opportunities and developments in the resources industry in Western Australia. -

Geometry and Genesis of the Giant Obuasi Gold Deposit, Ghana
Geometry and genesis of the giant Obuasi gold deposit, Ghana Denis Fougerouse, BSc, MSc This thesis is presented for the degree of Doctor of Philosophy. Centre for Exploration Targeting School of Earth and Environment The University of Western Australia July 2015 Supervisors: Dr Steven Micklethwaite Dr Stanislav Ulrich Dr John M Miller Professor T Campbell McCuaig ii "It never gets easier, you just go faster" Gregory James LeMond iv Abstract Abstract The supergiant Obuasi gold deposit is the largest deposit hosted in the Paleoproterozoic Birimian terranes of West Africa (62 Moz, cumulative past production and resources). The deposit is hosted in Kumasi Group sedimentary rocks composed of carbonaceous phyllites, slates, psammites, and volcaniclastic rocks intruded by different generations of felsic dykes and granites. In this study, the deformation history of the Obuasi district was re-evaluated and a three stage sequence defined based on observations from the regional to microscopic scale. The D1Ob stage is weakly recorded in the sedimentary rocks as a layer-parallel fabric. The D2Ob event is the main deformation stage and corresponds to a NW-SE shortening, involving tight to isoclinal folding, a pervasive subvertical S2Ob cleavage striking NE, as well as intense sub-horizontal stretching. Finally, a N-S shortening event (D3Ob) formed an ENE-striking, variably dipping S3Ob crenulation cleavage. Three ore bodies characteristic of the three main parallel mineralised trends were studied in details: the Anyankyerem in the Binsere trend; the Sibi deposit in the Gyabunsu trend, and the Obuasi deposit in the main trend. In the Obuasi deposit, two distinct styles of gold mineralisation occur; (1) gold-bearing sulphides, dominantly arsenopyrite, disseminated in metasedimentary rocks and (2) native gold hosted in quartz veins up to 25 m wide. -

Social, Environmental and Health Legacy Issues
MATERIAL ISSUE 4: The Nykabale village nursery is a project sponsored by AngloGold Ashanti to supply trees to the community and Geita Gold Mine, Tanzania. © 2014 ANGLOGOLD ASHANTI | ANNUAL REPORTS 2013 | Disclaimer MATERIAL ISSUE 4: Lung function testing at the occupational health clinic at Obuasi, Ghana. Context Occupational health and safety Occupational lung disease (OLD) is a risk inherent in many underground gold mines where silica dust is present. The most significant forms of OLD seen within the company are silicosis and pulmonary tuberculosis (TB). OLD in Brazil has virtually been eradicated, as a consequence of mechanisation of mining, improved ventilation, dust suppression, personal preventative measures and statutory limitations on the length of service of underground employees. If inhaled, silica dust may cause inflammation and scarring in the lungs, resulting in impaired lung functioning. Silicosis typically has a long latency period of more than 15 years and is sometimes only detected years after exposure. Silicosis in South Africa is a legacy issue on which AngloGold Ashanti and the gold mining industry as a whole, as well as government, unions and health care professionals place an enormous effort in addressing. Our occupational health strategy encompasses both minimising current risks, primarily by reducing occupational exposure within the industry. In 2008, we committed to eliminating new cases of silicosis among previously unexposed employees at our South African operations. Pulmonary TB, particularly where it is associated with silica dust exposure, is a key area of concern. Our immediate commitment is to reduce occupational TB incidence to below 2.25% among our South African employees and to successfully cure 85% of new cases – a target set by World Health Organization (WHO).