DOCSLIB.ORG

Lecture 8: Geometric and Binomial Distributions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 8: Geometric and Binomial Distributions Recap Dangling thread from last time From OpenIntro quiz 2: Lecture 8: Geometric and Binomial distributions Statistics 101 Mine C¸etinkaya-Rundel P(took j not valuable) September 22, 2011 P(took and not valuable) = P(not valuable) 0:1403 = 0:1403 + 0:5621 = 0:1997 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 1 / 27 Recap Geometric distribution Bernoulli distribution Milgram experiment Clicker question (graded) Stanley Milgram, a Yale University psychologist, conducted a series of Which of the following is false? experiments on obedience to authority starting in 1963. Experimenter (E) orders the teacher (a) The Z score for the mean of a distribution of any shape is 0. (T), the subject of the experiment, to (b) Half the observations in a distribution of any shape have positive give severe electric shocks to a Z scores. learner (L) each time the learner (c) The median of a right skewed distribution has a negative Z score. answers a question incorrectly. (d) Majority of the values in a left skewed distribution have positive Z The learner is actually an actor, and scores. the electric shocks are not real, but a prerecorded sound is played each time the teacher administers an electric shock. Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 2 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 3 / 27 Geometric distribution Bernoulli distribution Geometric distribution Bernoulli distribution Milgram experiment (cont.) Bernouilli random variables These experiments measured the willingness of study Each person in Milgram’s experiment can be thought of as a trial. participants to obey an authority figure who instructed them to A person is labeled a success if she refuses to administer a perform acts that conflicted with their personal conscience. severe shock, and failure if she administers such shock. Milgram found that about 65% of people would obey authority Since only 35% of people refused to administer a shock, and give such shocks. probability of success is p = 0:35. Over the years, additional research suggested this number is When an individual trial has only two possible outcomes, it is approximately consistent across communities and time. called a Bernoulli random variable. Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 4 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 5 / 27 Geometric distribution Bernoulli distribution Geometric distribution Geometric distribution Simulation of Milgram’s experiment Geometric distribution Dr. Smith wants to repeat Milgram’s experiments but she only wants to sam- Imagine a hat with 100 pieces of paper in it, 35 are marked “refuse” and 65 ple people until she finds someone who will not inflict a severe shock. What are marked “shock”. These represent the subjects in Milgram’s experiment. is the probability that she stops after the first person? > outcomes <- c(rep("refuse", 35), rep("shock", 65)) P(1st person refuses) = 0:35 Let’s simulate a sample of 10 subjects, with replacement so that the ... the third person? probability of success stays constant at 0.35 at each trial. S S R P(1st and 2nd shock; 3rd refuses) = × × > simSample <- sample(outcomes, size = 10, replace = TRUE) 0:65 0:65 0:35 = 0:652 × 0:35 ≈ 0:15 Now let’s take a look at who is in our simulated sample: ... the tenth person? > table(simSample) simSample The sample proportion of successes, th S S R 3 P(9 shock; 10 refuses) = × · · · × × shock refuse p^, is . 0:65 0:65 0:35 10 | {z } 7 3 9 of these = 0:659 × 0:35 ≈ 0:0072 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 6 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 7 / 27 Geometric distribution Geometric distribution Geometric distribution Geometric distribution Geometric distribution (cont.) Geometric distribution describes the waiting time until a success for independent and identically distributed (iid) Bernouilli random Clicker question variables. independence: outcomes of trials don’t affect each other Can we calculate the probability of rolling a 6 for the first time on the th identical: the probability of success is the same for each trial 6 roll of a die using the geometric distribution? (a) no, on the roll of a die there are more than 2 possible outcomes Geometric probabilities (b) yes, why not If p represents probability of success, (1 − p) represents probability of failure, and n represents number of independent trials P(success on the nth trial) = (1 − p)n−1p Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 8 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 9 / 27 Geometric distribution Geometric distribution Geometric distribution Geometric distribution Expected value Expected value and its variability Mean and standard deviation of geometric distribution s 1 1 − p How many people is Dr. Smith expected to test before finding the first µ = σ = one that refuses to administer the shock? p p2 The expected value, or the mean, of a geometric distribution is 1 Going back to Dr. Smith’s experiment: defined as p . 1 1 s r µ = = = 2:86 1 − p 1 − 0:35 p 0:35 σ = = = 2:3 p2 0:352 She is expected to test 2.86 people before finding the first one that refuses to administer the shock. But how can she test a non-whole Dr. Smith is expected to test 2.86 people before finding the first number of people? one that refuses to administer the shock, give or take 2.3 people. These values only makes sense in the context of repeating the experiment many many times. Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 10 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 11 / 27 Binomial distribution Binomial distribution The binomial distribution Suppose we randomly select four individuals to participate in Dr. Binomial distribution Smith’s experiment. What is the probability that exactly one of them will refuse to administer the shock? The question from the prior slide asked for the probability of given number of successes, k, in a given number of trials , n,(k = 1 Let’s call these people Allen (A), Brittany (B), Caroline (C), and success in n = 4 trials), and we calculated this probability as Damian (D). Each one of the four scenarios below will satisfy the condition of “exactly one of them refusing to administer the shock”: # of scenarios × P(single scenario) 1 A = refuse, B = shock, C = shock, D = shock: 0:35 ∗ 0:653 = 0:0961 2 A = shock, B = refuse, C = shock, D = shock: 0:35 ∗ 0:653 = 0:0961 # of scenarios: there is a less tedious way to figure this out, we’ll get to that shortly... 3 A = shock, B = shock, C = refuse, D = shock: 0:35 ∗ 0:653 = 0:0961 P(single scenario) = pk (1 − p)(n−k) 4 A = shock, B = shock, C = shock, D = refuse: 0:35 ∗ 0:653 = 0:0961 probability of success to the power of number of successes, probability of failure to the power of number of failures The probability of exactly one out of four people refusing to administer The binomial distribution describes the probability of having exactly k the shock is the sum of all of these probabilities. successes in n independent Bernouilli trials with probability of success p. 4 × 0:0961 = 0:3844 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 12 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 13 / 27 Binomial distribution The binomial distribution Binomial distribution The binomial distribution Counting the # of scenarios Calculating the # of scenarios Earlier we wrote out all possible scenarios that fit the condition of Choose function exactly one person refusing to administer the shock. If n was larger The choose function is useful for calculating the number of ways to and/or k was different than 1, writing out the scenarios would get choose k successes in n trials. even more tedious. For example, what if n = 9 and k = 2: ! n n! = RRSSSSSSS k k!(n − k)! SRRSSSSSS SSRRSSSSS 4 4! 4×3×2×1 ··· k = 1, n = 4: 1 = 1!(4−1)! = 1×(3×2×1) = 4 SSRSSRSSS 9 k = 2, n = 9: = 9! = 9×8×7! = 72 = 36 ··· 2 2!(9−1)! 2×1×7! 2 SSSSSSSRR Note: You can also use R for these calculations: Writing out all possible scenarios is way too tedious, and is prone to > choose(9,2) [1] 36 errors. Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 14 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 15 / 27 Binomial distribution The binomial distribution Binomial distribution The binomial distribution Properties of the choose function Binomial distribution (cont.) If k = 1, only 1 of the n trials result in a success, it could be the Binomial probabilities th first, the second, ··· , or the n trial, so there are n ways this can If p represents probability of success, (1 − p) represents probability of happen: failure, n represents number of independent trials, and k represents ! number of successes n = n ! 1 n P(k successes in n trials) = pk (1 − p)(n−k) If k = n, all n trials result in a success, and there’s only one way k this can happen: ! n We can use the binomial distribution to calculate the probability of k = 1 n successes in n trials, as long as If k = 0, all n trials result in a failure, and there’s only one way 1 the trials are independent this can happen as well: 2 the number of trials, n, is fixed ! 3 each trial outcome can be classified as a success or a failure n = 1 4 0 the probability of success, p, is the same for each trial Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 16 / 27 Statistics 101 (Mine C¸etinkaya-Rundel) L8: Geometric and Binomial September 22, 2011 17 / 27 Binomial distribution The binomial distribution Binomial distribution The binomial distribution Expected value Expected value and its variability A September 2011 Gallup survey suggests that 38% of Americans are Mean and standard deviation of binomial distribution planning on voting for Barack Obama in the 2012 presidential election.
Load more

Recommended publications
  • Discrete Probability Distributions Uniform Distribution Bernoulli
    Discrete Probability Distributions Uniform Distribution Experiment obeys: all outcomes equally probable Random variable: outcome Probability distribution: if k is the number of possible outcomes, 1 if x is a possible outcome p(x)= k ( 0 otherwise Example: tossing a fair die (k = 6) Bernoulli Distribution Experiment obeys: (1) a single trial with two possible outcomes (success and failure) (2) P trial is successful = p Random variable: number of successful trials (zero or one) Probability distribution: p(x)= px(1 − p)n−x Mean and variance: µ = p, σ2 = p(1 − p) Example: tossing a fair coin once Binomial Distribution Experiment obeys: (1) n repeated trials (2) each trial has two possible outcomes (success and failure) (3) P ith trial is successful = p for all i (4) the trials are independent Random variable: number of successful trials n x n−x Probability distribution: b(x; n,p)= x p (1 − p) Mean and variance: µ = np, σ2 = np(1 − p) Example: tossing a fair coin n times Approximations: (1) b(x; n,p) ≈ p(x; λ = pn) if p ≪ 1, x ≪ n (Poisson approximation) (2) b(x; n,p) ≈ n(x; µ = pn,σ = np(1 − p) ) if np ≫ 1, n(1 − p) ≫ 1 (Normal approximation) p Geometric Distribution Experiment obeys: (1) indeterminate number of repeated trials (2) each trial has two possible outcomes (success and failure) (3) P ith trial is successful = p for all i (4) the trials are independent Random variable: trial number of first successful trial Probability distribution: p(x)= p(1 − p)x−1 1 2 1−p Mean and variance: µ = p , σ = p2 Example: repeated attempts to start
    [Show full text]
  • Chapter 5 Sections
    Chapter 5 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions Continuous univariate distributions: 5.6 Normal distributions 5.7 Gamma distributions Just skim 5.8 Beta distributions Multivariate distributions Just skim 5.9 Multinomial distributions 5.10 Bivariate normal distributions 1 / 43 Chapter 5 5.1 Introduction Families of distributions How: Parameter and Parameter space pf /pdf and cdf - new notation: f (xj parameters ) Mean, variance and the m.g.f. (t) Features, connections to other distributions, approximation Reasoning behind a distribution Why: Natural justification for certain experiments A model for the uncertainty in an experiment All models are wrong, but some are useful – George Box 2 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Bernoulli distributions Def: Bernoulli distributions – Bernoulli(p) A r.v. X has the Bernoulli distribution with parameter p if P(X = 1) = p and P(X = 0) = 1 − p. The pf of X is px (1 − p)1−x for x = 0; 1 f (xjp) = 0 otherwise Parameter space: p 2 [0; 1] In an experiment with only two possible outcomes, “success” and “failure”, let X = number successes. Then X ∼ Bernoulli(p) where p is the probability of success. E(X) = p, Var(X) = p(1 − p) and (t) = E(etX ) = pet + (1 − p) 8 < 0 for x < 0 The cdf is F(xjp) = 1 − p for 0 ≤ x < 1 : 1 for x ≥ 1 3 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Binomial distributions Def: Binomial distributions – Binomial(n; p) A r.v.
    [Show full text]
  • (Introduction to Probability at an Advanced Level) - All Lecture Notes
    Fall 2018 Statistics 201A (Introduction to Probability at an advanced level) - All Lecture Notes Aditya Guntuboyina August 15, 2020 Contents 0.1 Sample spaces, Events, Probability.................................5 0.2 Conditional Probability and Independence.............................6 0.3 Random Variables..........................................7 1 Random Variables, Expectation and Variance8 1.1 Expectations of Random Variables.................................9 1.2 Variance................................................ 10 2 Independence of Random Variables 11 3 Common Distributions 11 3.1 Ber(p) Distribution......................................... 11 3.2 Bin(n; p) Distribution........................................ 11 3.3 Poisson Distribution......................................... 12 4 Covariance, Correlation and Regression 14 5 Correlation and Regression 16 6 Back to Common Distributions 16 6.1 Geometric Distribution........................................ 16 6.2 Negative Binomial Distribution................................... 17 7 Continuous Distributions 17 7.1 Normal or Gaussian Distribution.................................. 17 1 7.2 Uniform Distribution......................................... 18 7.3 The Exponential Density...................................... 18 7.4 The Gamma Density......................................... 18 8 Variable Transformations 19 9 Distribution Functions and the Quantile Transform 20 10 Joint Densities 22 11 Joint Densities under Transformations 23 11.1 Detour to Convolutions......................................
    [Show full text]
  • Lecture Notes #17: Some Important Distributions and Coupon Collecting
    EECS 70 Discrete Mathematics and Probability Theory Spring 2014 Anant Sahai Note 17 Some Important Distributions In this note we will introduce three important probability distributions that are widely used to model real- world phenomena. The first of these which we already learned about in the last Lecture Note is the binomial distribution Bin(n; p). This is the distribution of the number of Heads, Sn, in n tosses of a biased coin with n k n−k probability p to be Heads. As we saw, P[Sn = k] = k p (1 − p) . E[Sn] = np, Var[Sn] = np(1 − p) and p s(Sn) = np(1 − p). Geometric Distribution Question: A biased coin with Heads probability p is tossed repeatedly until the first Head appears. What is the distribution and the expected number of tosses? As always, our first step in answering the question must be to define the sample space W. A moment’s thought tells us that W = fH;TH;TTH;TTTH;:::g; i.e., W consists of all sequences over the alphabet fH;Tg that end with H and contain no other H’s. This is our first example of an infinite sample space (though it is still discrete). What is the probability of a sample point, say w = TTH? Since successive coin tosses are independent (this is implicit in the statement of the problem), we have Pr[TTH] = (1 − p) × (1 − p) × p = (1 − p)2 p: And generally, for any sequence w 2 W of length i, we have Pr[w] = (1 − p)i−1 p.
    [Show full text]
  • Discrete Probability Distributions Geometric and Negative Binomial Illustrated by Mitochondrial Eve and Cancer Driv
    Discrete Probability Distributions Geometric and Negative Binomial illustrated by Mitochondrial Eve and Cancer Driver/Passenger Genes Binomial Distribution • Number of successes in n independent Bernoulli trials • The probability mass function is: nx nx PX x Cpx 1 p for x 0,1,... n (3-7) Sec 3=6 Binomial Distribution 2 Geometric Distribution • A series of Bernoulli trials with probability of success =p. continued until the first success. X is the number of trials. • Compare to: Binomial distribution has: – Fixed number of trials =n. nx nx PX x Cpx 1 p – Random number of successes = x. • Geometric distribution has reversed roles: – Random number of trials, x – Fixed number of successes, in this case 1. n – Success always comes in the end: so no combinatorial factor Cx – P(X=x) = p(1‐p)x‐1 where: x‐1 = 0, 1, 2, … , the number of failures until the 1st success. • NOTE OF CAUTION: Matlab, Mathematica, and many other sources use x to denote the number of failures until the first success. We stick with Montgomery‐Runger notation 3 Geometric Mean & Variance • If X is a geometric random variable (according to Montgomery‐Bulmer) with parameter p, 1 1 p EX and 2 VX (3-10) pp2 • For small p the standard deviation ~= mean • Very different from Poisson, where it is variance = mean and standard deviation = mean1/2 Sec 3‐7 Geometric & Negative Binomial 4 Distributions Geometric distribution in biology • Each of our cells has mitochondria with 16.5kb of mtDNA inherited only from our mother • Human mtDNA has 37 genes encoding 13 proteins, 22+2 tRNA & rRNA • Mitochondria appeared 1.5‐2 billion years ago as a symbiosis between an alpha‐proteobacterium (1000s of genes) and an archaeaon (of UIUC’s Carl R.
    [Show full text]
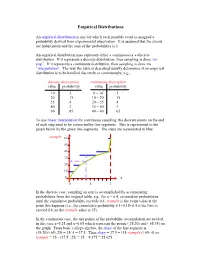
  • Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
    Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph.
    [Show full text]
  • Some Continuous and Discrete Distributions Table of Contents I
    Some continuous and discrete distributions Table of contents I. Continuous distributions and transformation rules. A. Standard uniform distribution U[0; 1]. B. Uniform distribution U[a; b]. C. Standard normal distribution N(0; 1). D. Normal distribution N(¹; ). E. Standard exponential distribution. F. Exponential distribution with mean ¸. G. Standard Gamma distribution ¡(r; 1). H. Gamma distribution ¡(r; ¸). II. Discrete distributions and transformation rules. A. Bernoulli random variables. B. Binomial distribution. C. Poisson distribution. D. Geometric distribution. E. Negative binomial distribution. F. Hypergeometric distribution. 1 Continuous distributions. Each continuous distribution has a \standard" version and a more general rescaled version. The transformation from one to the other is always of the form Y = aX + b, with a > 0, and the resulting identities: y b fX ¡ f (y) = a (1) Y ³a ´ y b FY (y) = FX ¡ (2) Ã a ! E(Y ) = aE(X) + b (3) V ar(Y ) = a2V ar(X) (4) bt MY (t) = e MX (at) (5) 1 1.1 Standard uniform U[0; 1] This distribution is \pick a random number between 0 and 1". 1 if 0 < x < 1 fX (x) = ½ 0 otherwise 0 if x 0 · FX (x) = x if 0 x 1 8 · · < 1 if x 1 ¸ E(X) = 1:=2 V ar(X) = 1=12 et 1 M (t) = ¡ X t 1.2 Uniform U[a; b] This distribution is \pick a random number between a and b". To get a random number between a and b, take a random number between 0 and 1, multiply it by b a, and add a. The properties of this random variable are obtained by applying¡ rules (1{5) to the previous subsection.
    [Show full text]
  • Probability Distributions
    Probability Distributions February 4, 2021 1 / 31 Deterministic vs Stochastic Models Until now, we have studied only deterministic models, in which future states are entirely specified by the current state of the system. In the real world, however, chance plays a major role in the dynamics of a population. Lightning may strike an individual. A fire may decimate a population. Individuals may fail to reproduce or produce a bonanza crop of offspring. New beneficial mutations may, by happenstance, occur in individuals that leave no children. Drought and famine may occur, or rains and excess. Probabilistic models include chance events and outcomes and can lead to results that differ from purely deterministic models. 2 / 31 Probability Distributions In this section, we will introduce the concept of a random variable and examine its probability distribution, expectation, and variance. Consider an event or series of events with a variety of possible outcomes. We define a random variable that represents a particular outcome of these events. Random variables are generally denoted by capital letters, e.g., X , Y , Z. For instance, toss a coin twice and record the number of heads. The number of heads is a random variable and it may take on three values: X = 0 (no heads), X = 1 (one head), and X = 2 (two heads). First, we will consider random variables, as in this example, which have only a discrete set of possible outcomes (e.g., 0, 1, 2). 3 / 31 Probability Distributions In many cases of interest, one can specify the probability distribution that a random variable will follow.
    [Show full text]
  • A Compound Class of Geometric and Lifetimes Distributions
    Send Orders of Reprints at [email protected] The Open Statistics and Probability Journal, 2013, 5, 1-5 1 Open Access A Compound Class of Geometric and Lifetimes Distributions Said Hofan Alkarni* Department of Quantitative Analysis, King Saud University, Riyadh, Saudi Arabia Abstract: A new lifetime class with decreasing failure rateis introduced by compounding truncated Geometric distribution and any proper continuous lifetime distribution. The properties of the proposed class are discussed, including a formal proof of its probability density function, distribution function and explicit algebraic formulae for its reliability and failure rate functions. A simple EM-type algorithm for iteratively computing maximum likelihood estimates is presented. A for- mal equation for Fisher information matrix is derived in order to obtaining the asymptotic covariance matrix. This new class of distributions generalizes several distributions which have been introduced and studied in the literature. Keywords: Lifetime distributions, decreasing failure rate, Geometric distribution. 1. INTRODUCTION and exponential with DFR was introduced by [7]. The expo- nential-Poisson (EP) distribution was proposed by [8] and The study of life time organisms, devices, structures, ma- generalized [9] using Wiebull distribution and the exponential- terials, etc., is of major importance in the biological and en- logarithmic distribution discussed by [10]. A two-parameter gineering sciences. A substantial part of such study is de- distribution family with decreasing
    [Show full text]
  • Geometric, Negative Binomial Distributions
    Geometric Distribution We will discuss two distributions in this section, both which have two parameterizations, so we must be careful. Suppose you roll a single die until you roll a 6. Let us consider \rolling a 6" a \success" and \not rolling a 6" a \failure". Our goal is to determine a distribution for the total number of rolls necessary to roll a 6. However, we can also write a distribution for the number of failures that occur, rather than the number of total rolls. Counting the number of failures results in a simpler probability formula, so this is what is typically used. The situation above, regardless of which term you count (number of failures or number of rolls) is a geo- metric distribution. We will derive the probability formula for this distribution, because it will help us get a feel for deriving the formula for the next distribution as well. Let X = the number of failures before the first success - in this case, the number of non-six rolls prior to 1 1 5 rolling a 6. The probability of rolling a 6 is 6 and the probability of a non-6 is 1 − 6 = 6 . Then, 1 50 1 P (X = 0) = = · Since there are no failures, we immediately succeed. 6 6 6 5 1 51 1 P (X = 1) = · = · Here we fail once, and then succeed. 6 6 6 6 5 5 1 52 1 P (X = 2) = · · = · Here we fail twice, and then succeed. 6 6 6 6 6 5 5 5 1 53 1 P (X = 3) = · · · = · Here we fail three times in a row, and then succeed.
    [Show full text]
  • Discrete Random Variables and Probability Distributions
    Discrete Random 3 Variables and Probability Distributions Stat 4570/5570 Based on Devore’s book (Ed 8) Random Variables We can associate each single outcome of an experiment with a real number: We refer to the outcomes of such experiments as a “random variable”. Why is it called a “random variable”? 2 Random Variables Definition For a given sample space S of some experiment, a random variable (r.v.) is a rule that associates a number with each outcome in the sample space S. In mathematical language, a random variable is a “function” whose domain is the sample space and whose range is the set of real numbers: X : R S ! So, for any event s, we have X(s)=x is a real number. 3 Random Variables Notation! 1. Random variables - usually denoted by uppercase letters near the end of our alphabet (e.g. X, Y). 2. Particular value - now use lowercase letters, such as x, which correspond to the r.v. X. Birth weight example 4 Two Types of Random Variables A discrete random variable: Values constitute a finite or countably infinite set A continuous random variable: 1. Its set of possible values is the set of real numbers R, one interval, or a disjoint union of intervals on the real line (e.g., [0, 10] ∪ [20, 30]). 2. No one single value of the variable has positive probability, that is, P(X = c) = 0 for any possible value c. Only intervals have positive probabilities. 5 Probability Distributions for Discrete Random Variables Probabilities assigned to various outcomes in the sample space S, in turn, determine probabilities associated with the values of any particular random variable defined on S.
    [Show full text]
  • A Spreadsheet-Literate Non-Statistician's Guide to the Beta
    A Spreadsheet-Literate Non-Statistician’s Guide to the Beta-Geometric Model Peter S. Fader www.petefader.com Bruce G. S. Hardie† www.brucehardie.com December 2014 1 Introduction The beta-geometric (BG) distribution is a robust simple model for characterizing and forecasting the length of a customer’s relationship with a firm in a contractual setting. Fader and Hardie (2007a), hereafter FH, is a definitive reference, providing a detailed derivation of the key quantities of interest, as well as step-by-step details of how to implement the model in Excel. However the statistical concepts and notation used in that paper can be daunting for those analysts who do not have a strong statistics background, leading them to ignore the model when it should really be a basic tool in their analytics toolkit. With spreadsheet-literate non-statisticians in mind as the target audience, the objective of this note is to describe the logic of the BG model in a non-technical manner and show how to implement it in Excel. 2 Motivating Problem Consider a company with a subscription-based business model that acquired 1000 customers (on annual contracts) at the beginning of Year 1. Table 1 reports the pattern of renewals by this cohort over the subsequent four years.1 We would like to predict how many members of this cohort will still be customers of the firm in Years 6, 7, .... † c 2014 Peter S. Fader and Bruce G. S. Hardie. This document and the associated spreadsheet (BG intro.xlsx) can be found at <http://brucehardie.com/notes/032/>.
    [Show full text]