Improving ASTER GDEM Accuracy Using Land Use-Based Linear Regression Methods: a Case Study of Lianyungang, East China
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rapid Urbanization in Eastern China: Roles for SEA
Rapid Urbanization in Eastern China: Roles for SEA Peter Mulvihill (York University) & Yangfan Li (Nanjing University) 1. Introduction In this paper we explore possibilities for an expanded role for Strategic Environmental Assessment (SEA) in addressing and preventing problems caused by rapid urbanization in coastal areas of China. 2. Context The torrid pace of economic development in many parts of China is well recognized, and its accompanying array of ecological and social impacts is increasingly well documented. Despite attempts to identify, avoid or minimize these negative effects through EIA, policy and related planning processes, irreversible impacts occur, often in cumulative ways that are not understood completely. This syndrome is particularly acute in China’s coastal regions, where rapid urbanization is transforming landscapes and ecosystems at an unprecedented pace. There is considerable hope that SEA can help improve planning and development processes, thus overcoming some of the characteristic shortcomings of more conventional forms of environmental assessment. The premise that SEA can be a proactive, sustainability-focused process is undeniably attractive. However, the gathering literature on SEA suggests strongly that there are still many implementation challenges to be overcome before this relatively new form of EA can reach its potential. SEA has been practiced in China since 2003. Bina (2008) has identified several recurring problems with the early implementation of SEA in China: it tends to be applied late in the planning process, and is therefore reactive to plans instead of influencing their formulation; like conventional project-driven EA, it is mostly mitigation-focused; there is little public participation; and there is a strong natural sciences and engineering bias in the process. -

Table of Codes for Each Court of Each Level
Table of Codes for Each Court of Each Level Corresponding Type Chinese Court Region Court Name Administrative Name Code Code Area Supreme People’s Court 最高人民法院 最高法 Higher People's Court of 北京市高级人民 Beijing 京 110000 1 Beijing Municipality 法院 Municipality No. 1 Intermediate People's 北京市第一中级 京 01 2 Court of Beijing Municipality 人民法院 Shijingshan Shijingshan District People’s 北京市石景山区 京 0107 110107 District of Beijing 1 Court of Beijing Municipality 人民法院 Municipality Haidian District of Haidian District People’s 北京市海淀区人 京 0108 110108 Beijing 1 Court of Beijing Municipality 民法院 Municipality Mentougou Mentougou District People’s 北京市门头沟区 京 0109 110109 District of Beijing 1 Court of Beijing Municipality 人民法院 Municipality Changping Changping District People’s 北京市昌平区人 京 0114 110114 District of Beijing 1 Court of Beijing Municipality 民法院 Municipality Yanqing County People’s 延庆县人民法院 京 0229 110229 Yanqing County 1 Court No. 2 Intermediate People's 北京市第二中级 京 02 2 Court of Beijing Municipality 人民法院 Dongcheng Dongcheng District People’s 北京市东城区人 京 0101 110101 District of Beijing 1 Court of Beijing Municipality 民法院 Municipality Xicheng District Xicheng District People’s 北京市西城区人 京 0102 110102 of Beijing 1 Court of Beijing Municipality 民法院 Municipality Fengtai District of Fengtai District People’s 北京市丰台区人 京 0106 110106 Beijing 1 Court of Beijing Municipality 民法院 Municipality 1 Fangshan District Fangshan District People’s 北京市房山区人 京 0111 110111 of Beijing 1 Court of Beijing Municipality 民法院 Municipality Daxing District of Daxing District People’s 北京市大兴区人 京 0115 -

Annual Report 2013 Contents
AMITY A member of Annual Report 2013 Contents 01 A Message from the General Secretary 03 Project Reports 03 Church and Social Services 07 Community Development, Disaster Management, Environmental Protection, HIV/AIDS Prevention and Public Health 11 Education and Orphan Fostering 15 Education and International Exchange 20 Social Welfare 24 NGO Development 28 Urban Community Services 31 Resource Development 34 Amity Foundation, Hong Kong 43 Amity Printing Co., Ltd. 45 Who We Are 45 Organizational Chart 46 Amity Staff 47 Statistics 47 Where the funds come from 47 Where the funds go 48 List of Institutional Partners 55 Auditors Reports 2013 AMITY 01 A Message from the General Secretary In mid-January 2014, the Center for Civil Society Studies of Peking University announced Top Ten Events in Social Sectors in China 2013, among which were direct registration of four types of NGOs as a result of reforming the dual management system, population policy shift from quantity control to structure optimization remarked by the adoption of two-child fertility policy for couples where either the husband or the wife is from a single child family, citizens’ actions urging the government to share the responsibility to address the haze-highlighted environmental problems, Rule of Law in China as a resolution of the 3rd Plenary Session of 18th CPC Central Committee accompanied by a nationwide debate on political and legal basis for China Dream, and smoother cooperation between NGOs and the government occurring during Ya'an earthquake where the emergency response mechanism for disaster relief was challenged. Reading through the Top Ten Events, we find that more and more public voices were heard and taken seriously and eventually became driving forces to social development. -
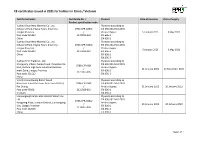
CE Certificates Issued in 2021 for Holders in China / Vietnam
CE certificates issued in 2021 for holders in China / Vietnam Certificate holder Certificate No. / Product Date of issuance Date of expiry Product specification code Xuzhou Yizun New Material Co., Ltd. Plywood according to Industrial Park, Hegou Town, Xinyi City, 0766-CPR-429/4 EN 636:2012+A1:2015 Jiangsu Province / Product types: 5 January 2021 9 May 2021 Post code 221439 2117181-009 EN 636-1 China EN 636-2 Xuzhou Yizun New Material Co., Ltd. Plywood according to Industrial Park, Hegou Town, Xinyi City, 0766-CPR-430/4 EN 636:2012+A1:2015 Jiangsu Province / Product types: 5 January 2021 9 May 2021 Post code 221439 2117181-010 EN 636-1 China EN 636-2 EN 636-3 Xuzhou Kinri Trade Co., Ltd. Plywood according to Shengyang Village, Sanpu Town, Tongshan Dis- EN 636:2012+A1:2015 0766-CPR-564 trict, Xuzhou High-tech Industrial Develop- Product types: / 11 January 2021 24 November 2021 ment Zone, Jiangsu Province EN 636-1 2121007-005 Post code 221112 EN 636-2 China Viet Nam Hai Duong Baifar Wood Plywood according to Nam Sach Industrial Zone, Nam Sach District, 0766-CPR-565 EN 636:2012+A1:2015 Hai Duong / Product types: 11 January 2021 10 January 2022 Post code 03000 2121008-001 EN 636-1 Vietnam EN 636-2 LianyungangChanta International Wood Cov Plywood according to Ltd. EN 636:2012+A1:2015 0766-CPR-485/2 Kangpeng Plaza, Lianyun District, Lianyungang Product types: / 26 January 2021 20 January 2022 City, Jiangsu Province EN 636-1 2119007-003 Post code 222000 EN 636-2 China EN 636-3 Page 1 of 7 CE certificates issued in 2021 for holders in China / Vietnam Certificate holder Certificate No. -

Ceramic Tableware from China List of CNCA‐Certified Ceramicware
Ceramic Tableware from China June 15, 2018 List of CNCA‐Certified Ceramicware Factories, FDA Operational List No. 64 740 Firms Eligible for Consideration Under Terms of MOU Firm Name Address City Province Country Mail Code Previous Name XIAOMASHAN OF TAIHU MOUNTAINS, TONGZHA ANHUI HANSHAN MINSHENG PORCELAIN CO., LTD. TOWN HANSHAN COUNTY ANHUI CHINA 238153 ANHUI QINGHUAFANG FINE BONE PORCELAIN CO., LTD HANSHAN ECONOMIC DEVELOPMENT ZONE ANHUI CHINA 238100 HANSHAN CERAMIC CO., LTD., ANHUI PROVINCE NO.21, DONGXING STREET DONGGUAN TOWN HANSHAN COUNTY ANHUI CHINA 238151 WOYANG HUADU FINEPOTTERY CO., LTD FINEOPOTTERY INDUSTRIAL DISTRICT, SOUTH LIUQIAO, WOSHUANG RD WOYANG CITY ANHUI CHINA 233600 THE LISTED NAME OF THIS FACTORY HAS BEEN CHANGED FROM "SIU‐FUNG CERAMICS (CHONGQING SIU‐CERAMICS) CO., LTD." BASED ON NOTIFICATION FROM CNCA CHONGQING CHN&CHN CERAMICS CO., LTD. CHENJIAWAN, LIJIATUO, BANAN DISTRICT CHONGQING CHINA 400054 RECEIVED BY FDA ON FEBRUARY 8, 2002 CHONGQING KINGWAY CERAMICS CO., LTD. CHEN JIA WAN, LI JIA TUO, BANAN DISTRICT, CHONGQING CHINA 400054 BIDA CERAMICS CO.,LTD NO.69,CHENG TIAN SI GE DEHUA COUNTY FUJIAN CHINA 362500 NONE DATIAN COUNTY BAOFENG PORCELAIN PRODUCTS CO., LTD. YONGDE VILLAGE QITAO TOWN DATIAN COUNTY CHINA 366108 FUJIAN CHINA DATIAN YONGDA ART&CRAFT PRODUCTS CO., LTD. NO.156, XIANGSHAN ROAD, JUNXI TOWN, DATIAN COUNTY FUJIAN 366100 DEHUA KAIYUAN PORCELAIN INDUSTRY CO., LTD NO. 63, DONGHUAN ROAD DEHUA TOWN FUJIAN CHINA 362500 THE LISTED ADDRESS OF THIS FACTORY HAS BEEN CHANGED FROM "MAQIUYANG XUNZHONG XUNZHONG TOWN, DEHUA COUNTY" TO THE NEW EAST SIDE, THE SECOND PERIOD, SHIDUN PROJECT ADDRESS LISTED ABOVE BASED ON NOTIFICATION DEHUA HENGHAN ARTS CO., LTD AREA, XUNZHONG TOWN, DEHUA COUNTY FUJIAN CHINA 362500 FROM THE CNCA AUTHORITY IN SEPTEMBER 2014 DEHUA HONGSHENG CERAMICS CO., LTD. -

Global Sourcing Map Factory List - Bangladesh
Information last updated July 2018 Global Sourcing Map Factory List - Bangladesh Factory Name Address Country Total Men Women Number of Workers Afiya Knitwear Ltd 10/ 2 Durgapur Ashulia Savar Dhaka 1341 Bangladesh 579 288 (49.7)% 291 (50.3)% AKH Apparels Ltd 128 Hemayetpur Savar Dhaka 1340 Bangladesh 2188 971 (44.4)% 1217 (55.6)% AKH Eco Apparels Ltd 495 Balitha Shah-Belishwer Dhamrai Dhaka 1800 Bangladesh 5418 3000 (55.4)% 2418 (44.6)% Alpha Knitting Wear Limited 888 Shewrapara, 1St & 2Nd Floor Begum Rokeya Shoroni Mirpur Dhaka 1216 Bangladesh 2307 682 (29.6)% 1625 (70.4)% Ananta Denim Technology Ltd Noyabari Kanchpur Sonargaon Narayanganj Bangladesh 4833 2394 (49.5)% 2439 (50.5)% Ananta Huaxiang Ltd 222, 223, H2-H4, Adamjee Epz Shiddirgonj Narayanganj Dhaka Bangladesh 2039 1184 (58.1)% 855 (41.9)% Anowara Knit Composite Ltd Mulaid Mawna Sreepur Gazipur Bangladesh 1979 1088 (55.0)% 891 (45.0)% Apex Lingerie Limited Chandora Kaliakoir Gazipur Bangladesh 3937 2041 (51.8)% 1896 (48.2)% Arunima Sportswear Ltd Dewan Idris Road Zirabo Ashulia Savar Dhaka Bangladesh 4481 2561 (57.2)% 1920 (42.8)% Primark does not own any factories and is selective about the suppliers with whom we work. Every factory which manufactures product for Primark has to commit to meeting internationally recognised standards, before the first order is placed and throughout the time they work with us. The factories featured on Primark’s Global Sourcing Map are Primark’s suppliers’ production sites which represent over 95% of Primark products for sale in Primark stores. A factory is detailed on the Map only after it has produced products for Primark for a year and has become an established supplier. -

Major Chinese Industrial Companies
AllChinaReports.com Industry Reports, Company Reports & Industry Analysis Directory: Major Chinese Industrial Companies ● 186 Industries ● 1435 Top Companies ● 999 Company Websites Beijing Zeefer Consulting Ltd. April 2012 Disclaimer Authorized by: Beijing Zeefer Consulting Ltd. Company Site: http://www.Zeefer.org Online Store of China Industry Reports: http://www.AllChinaReports.com Beijing Zeefer Consulting Ltd. and (or) its affiliates (hereafter, "Zeefer") provide this document with the greatest possible care. Nevertheless, Zeefer makes no guarantee whatsoever regarding the accuracy, utility, or certainty of the information in this document. Further, Zeefer disclaims any and all responsibility for damages that may result from the use or non-use of the information in this document. The information in this document may be incomplete and/or may differ in expression from other information in elsewhere by other means. The information contained in this document may also be changed or removed without prior notice. Table of Contents CIC Code Industry Page 0610 Coal Mining 1 0620 Lignite Mining 2 0690 Other Coal Mining 3 0710 Crude Petroleum & Natural Gas Extraction 3 0810 Iron Ores Mining 5 1320 Feed Processing 6 1331 Edible Vegetable Oil Processing 7 1332 Inedible Vegetable Oil Processing 8 1340 Sugar Mfg. 9 1351 Livestock & Poultry Slaughtering 10 1352 Meat Processing 11 1361 Frozen Aquatic Products Processing 12 1411 Pastry & Bread Mfg. 13 1419 Biscuit & Other Baked Foods Mfg. 14 1421 Candy & Chocolate Mfg. 16 1422 Preserved Fruits Mfg. 17 1431 Rice & Flour Products Mfg. 18 1432 Quick Frozen Foods Mfg. 19 1439 Instant Noodle & Other Convenient Foods Mfg. 21 1440 Liquid Dairy & Dairy Products Mfg. -

A Review of China Coastal Waterbird Surveys 2005
Bai et al. Avian Research (2015) 6:12 DOI 10.1186/s40657-015-0021-2 RESEARCH Open Access Identification of coastal wetlands of international importance for waterbirds: a review of China Coastal Waterbird Surveys 2005–2013 China Coastal Waterbird Census Group, Qingquan Bai1*, Jianzhong Chen2, Zhihong Chen3, Guotai Dong3, Jiangtian Dong4, Wenxiao Dong5, Vivian Wing Kan Fu6, Yongxiang Han7, Gang Lu8, Jing Li9, Yang Liu10, Zhi Lin3,11, Derong Meng12, Jonathan Martinez13, Guanghui Ni14, Kai Shan15, Renjie Sun16, Suixing Tian4, Fengqin Wang2,17, Zhiwei Xu3, Yat-tung Yu6, Jin Yang14, Zhidong Yang18, Lin Zhang19, Ming Zhang20 and Xiangwu Zeng21 Abstract Background: China’s coastal wetlands belong to some of the most threatened ecosystems worldwide. The loss and degradation of these wetlands seriously threaten waterbirds that depend on wetlands. Methods: The China Coastal Waterbird Census was organized by volunteer birdwatchers in China’s coastal region. Waterbirds were surveyed synchronously once every month at 14 sites, as well as irregularly at a further 18 sites, between September 2005 and December 2013. Results: A total of 75 species of waterbirds met the 1 % population level Ramsar listing criterion at least once at one site. The number of birds of the following species accounted for over 20 % of the total flyway populations at a single site: Mute Swan (Cygnus olor), Siberia Crane (Grus leucogeranus), Far Eastern Oystercatcher (Haematopus osculans), Bar-tailed Godwit (Limosa lapponica), Spotted Greenshank (Tringa guttifer), Great Knot (Calidris tenuirostris), Spoon-billed Sandpiper (Calidris pygmeus), Saunders’s Gull (Larus saundersi), Relict Gull (Larus relictus), Great Cormorant (Phalacrocorax carbo), Eurasian Spoonbill (Platalea leucorodia), Black-faced Spoonbill (Platalea minor) and Dalmatian Pelican (Pelecanus crispus). -

Initiative on Philanthropy in China
Do not quote or cite without author's permission Initiative on Philanthropy in China Community Foundations in China: In Search of an Identity? by Chao Guo Associate Professor School of Social Policy & Practice University of Pennsylvania Weijun Lai Department of Sociology Chinese University of Hong Kong China Philanthropy Summit Research Center for Chinese Politics & Business and Lilly Family School of Philanthropy Indiana University Indianapolis, Indiana October 31-November 1, 2014 © Indiana University Research Center for Chinese Politics & Business and the Lilly Family School of Philanthropy Working paper draft – October 2014 – Not for distribution Community Foundations in China: In Search of Identity? Chao Guo and Weijun Lai1 Since the government launched its economic and political reforms over thirty five years ago, China’s civil society sector has begun to re-emerge along with the Chinese people’s renewed quest for democracy. Economically aggressive but politically conservative, the Chinese government has been suspicious of the motives and consequences of both movements. It is thus not a coincidence that the ups and downs of the nonprofit sector often mirror those of democratization from year to year. Despite the constant pressures from the state, however, the growth of the nonprofit sector seems irreversible: today, there are close to half million officially registered nonprofit organizations (NPOs) with nearly 6 million employees, as well as millions of unregistered grassroots organizations (Guo, Xu, Smith, & Zhang, 2012; see also Deng, 2014; Zhu, 2014). It is against this backdrop that the current study reports on findings from our research on community foundations in China. Our interest in community foundations was heightened by two recent developments in the field of philanthropy in China. -

Annual Development Report on China's Trademark Strategy 2013
Annual Development Report on China's Trademark Strategy 2013 TRADEMARK OFFICE/TRADEMARK REVIEW AND ADJUDICATION BOARD OF STATE ADMINISTRATION FOR INDUSTRY AND COMMERCE PEOPLE’S REPUBLIC OF CHINA China Industry & Commerce Press Preface Preface 2013 was a crucial year for comprehensively implementing the conclusions of the 18th CPC National Congress and the second & third plenary session of the 18th CPC Central Committee. Facing the new situation and task of thoroughly reforming and duty transformation, as well as the opportunities and challenges brought by the revised Trademark Law, Trademark staff in AICs at all levels followed the arrangement of SAIC and got new achievements by carrying out trademark strategy and taking innovation on trademark practice, theory and mechanism. ——Trademark examination and review achieved great progress. In 2013, trademark applications increased to 1.8815 million, with a year-on-year growth of 14.15%, reaching a new record in the history and keeping the highest a mount of the world for consecutive 12 years. Under the pressure of trademark examination, Trademark Office and TRAB of SAIC faced the difficuties positively, and made great efforts on soloving problems. Trademark Office and TRAB of SAIC optimized the examination procedure, properly allocated examiners, implemented the mechanism of performance incentive, and carried out the “double-points” management. As a result, the Office examined 1.4246 million trademark applications, 16.09% more than last year. The examination period was maintained within 10 months, and opposition period was shortened to 12 months, which laid a firm foundation for performing the statutory time limit. —— Implementing trademark strategy with a shift to effective use and protection of trademark by law. -
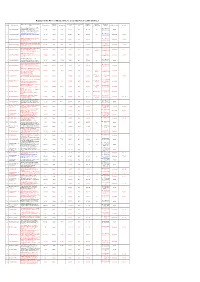
FSC Cert Register ENG
Register of the FSC certificate holders, issued by Forest certification LLC Name, location, address of the certificate Certificate Date of certificate Year of certificate Certificate Previous Certification Sl.No. Certificate code Certificate type Forest plot area Certificate status Remarks holder type(2) issue issue validity date certificate code standart "ResursLesTrans" OOO (LLC), 665756, FSC-STD-RUS- 1 FC-FM/COC-643001 Irkutskaya Oblast, Bratskiy Rayon, FM/COC SinGle 25395 03.12.13 2013 02.12.18 — Issued V6-1-2012 v.6.01 Shumilovo Township, NaGornaya St., 23 "Del’ta-Plyus" OOO (LLC), 665717, FSC-STD-RUS- 2 FC-FM/COC-643002 Irkutskaya Oblast, Bratsk, Grazhdanskaya FM/COC SinGle 36060 07.02.13 2013 06.02.18 — Suspended 19.10.16 V6-1-2012 v.6.01 St., 35 "Baykal" OOO (LLC), 665771, Irkutskaya FSC-STD-RUS- 3 FC-FM/COC-643003 Oblast, Bratskiy Rayon, Vikhorevka, FM/COC SinGle 79909 20.03.13 2013 19.03.18 — Terminated 27.07.16 V6-1-2012 v.6.01 Dokovskaya St., 22/13 "Regional’naya lesnaya kompaniya" ZAO FSC-STD-RUS- 4 FC-FM/COC-643004 (CJSC), 665640, Irkutskaya Oblast, Bratskiy FM/COC SinGle 27978 12.05.14 2014 11.05.19 — Terminated 24.10.15 V6-1-2012 v.6.01 Rayon, Mamyr’ Township "Badinskiy KLPKh" OAO (OJSC), 665740, EP-FM/COC- FSC-STD-RUS- 5 FC-FM/COC-643005 Irkutskaya Oblast, Bratskiy Rayon, FM/COC SinGle 123647 31.03.09 2009 10.11.12 Terminated 10.11.12 643013 V6-1-2012 v.6.01 Pokosnoe Township, Sibirskaya St., 18 "Chart" OOO (LLC), 187000, FSC-STD-RUS- 6 FC-FM/COC-643006 LeninGradskaya Oblast, Tosno, Moskovskoe FM/COC SinGle 4987 31.03.12 -

Event Guide Your Platform in China to Meet the Global Container Shipping and Logistics Market
22-24 MAY 2019 SWEECC | SHANGHAI EVENT GUIDE YOUR PLATFORM IN CHINA TO MEET THE GLOBAL CONTAINER SHIPPING AND LOGISTICS MARKET www.intermodal-asia.com Organised by: Supported by: Follow us on: FLOORPLAN & EXHIBITOR A-Z 3M CHINA CO. LTD L51 RHENUS Intermodal SYSTEMS LZ31 7SEAS LOGISTICS LTD NETWORKING AREA SPONSOR, E71 J71 A71 D71 D73 E71F73 F71 G73 H71 OPENING Seaco Global LIMITED H01 MEDIA ZONE CEREMONY C71 INTERNET AND CHARGING ZONE ABN AMRO LanYARD SPONSOR 7 SEAS Seacube CONTAINERS LLC J01 D63 LOGISTICS F61 G67 G65 H63 INNOVATION A.C.S.T Chemical (KUNSHAN) CO., LTD. C41 LZ41 LZ43 LZ48 NETWORKING THEATRE TRIDENT SealocK SECURITY SYSTEMS K45 CCIA AREA ABS A11 LZ42 LZ46 SEATING AREA G63 G61 SHANDONG QINGYUN COUNTY JUNCHUANG Adani PORTS & SEZ LZ36 Logistics Zone LOCK INDUSTRIAL CO., LTD E55 ILSS LZ35 LZ47 THEATRE LZ36 D53 E55E53 F51F55 F57 G51 G55 H53 J51 J53 J57 K55 AIM CONTAINER Service LIMITED E51 LZ31 LZ32LZ33 LZ34 SHANGHAI CHANGJIN MACHINERY EQUIPMENT CO., LTD. A31 E51 F53 G53 H51 J55 K51 L59 ALL PAKISTAN Shipping Association (APSA) LZ42 SHANGHAI GROW UP Electromechanical C47 C45 C43 D41 E41F41 G41 H41 J61 J45 J47 EQUIPMENT CO., LTD L55 Baojun NEW BUILDING Materials (TIANJIN)CO.,LTD G41 L51L55 C41 J41 Beacon Intermodal LEASING B01 J43 L53L50 SHANGHAI HAOLI COATINGS CO., LTD. C33 BEIJING RUI LI HENG YI LOGISTICS Technology PLC J53 SHANGHAI Xinfan INDUSTRIAL Corporation J35 C31 C33 A41 F25 G31 H31 A35 B21 INTERMODAL ASIA & J35 J37 K45 INTERMODAL EUROPE / SEATING AREA BEIJING TRANS EURASIA International VIP & SPEAKER LOUNGE K41 SHEN JOINT Technology CO., LTD J33 K47 G53 A31 J31 LOGISTICS CO., LTD LZ34 D21 F21 SHENZHEN BLUE OCEAN ENGINEERING BIP Perolo JIANGSU ENGINEERING LIMITED J25 L27L28 L22 C21 G25 G23 H21 J21 J25 Development CO.LTD L19 A23 L24 TECH BLUE SKY Intermodal F61 ZONE L23 J23 M21 SHENZHEN CONCOX Information Technology A21 L21L25 Bureau International DES CONTAINERS (BIC) K47 G21 CO., LTD.