Spline Joints for Multibody Dynamics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Proximal Interphalangeal Joint: Arthritis and Deformity
4.1800EOR0010.1302/2058-5241.4.180042 research-article2019 EOR | volume 4 | June 2019 DOI: 10.1302/2058-5241.4.180042 Instructional Lecture: Hand & Wrist www.efortopenreviews.org The proximal interphalangeal joint: arthritis and deformity Daniel Herren Finger joints are of the most common site of osteoarthritis Most authors, especially in the rheumatology and arthritis and include the DIP, PIP and the thumb saddle joint. literature, use a modification of the Kellgren and Lawrence 1 Joint arthroplasty provides the best functional outcome scale, initially described for patellofemoral arthritis, for for painful destroyed PIP joints, including the index finger. radiographic classification: Adequate bone stock and functional tendons are required for a successful PIP joint replacement Grade 1: doubtful narrowing of joint space and pos- sible osteophytic lipping Fixed swan-neck and boutonnière deformity are better served with PIP arthrodesis rather than arthroplasty. Grade 2: definite osteophytes, definite narrowing of joint space Silicone implants are the gold standard in terms of implant choice. Newer two-component joints may have potential Grade 3: moderate multiple osteophytes, definite nar- to correct lateral deformities and improve lateral stability. rowing of joint space, some sclerosis and possible deformation of bone contour Different surgical approaches are used for PIP joint implant arthroplasty according to the needs and the experience of Grade 4: large osteophytes, marked narrowing of joint the surgeon. space, severe sclerosis and definite deformation of bone contour Post-operative rehabilitation is as critical as the surgical procedure. Early protected motion is a treatment goal. Revision and exchange PIP arthroplasty may successfully Treatment be used to treat chronic pain, but will not correct defor- mity. -

Module 6 : Anatomy of the Joints
Module 6 : Anatomy of the Joints In this module you will learn: About the classification of joints What synovial joints are and how they work Where the hinge joints are located and their functions Examples of gliding joints and how they work About the saddle joint and its function 6.1 Introduction The body has a need for strength and movement, which is why we are rigid. If our bodies were not made this way, then movement would be impossible. We are designed to grow with bones, tendons, ligaments, and joints that all play a part in natural movements known as articulations – these strong connections join up bones, teeth, and cartilage. Each joint in our body makes these links possible and each joint performs a specific job – many of them differ in shape and structure, but all control a range of motion between the body parts that they connect. 6.2 Classifying Joints Joints that do not allow movement are known as synarthrosis joints. Examples of synarthroses are sutures of the skull, and the gomphoses which connect our teeth to the skull. Amphiarthrosis joints allow a small range of movement, an example of this is your intervertebral discs attached to the spine. Another example is the pubic symphysis in your hip region. The freely moving joints are classified as diarthrosis joints. These have a higher range of motion than any other type of joint, they include knees, elbows, shoulders, and wrists. Joints can also be classified depending on the kind of material each one is structurally made up of. A fibrous joint is made up of tough collagen fiber, examples of this are previously mentioned sutures of the skull or the syndesmosis joint, which holds the ulna and radius of your forearm in place. -

Joints Classification of Joints
Joints Classification of Joints . Functional classification (Focuses on amount of movement) . Synarthroses (immovable joints) . Amphiarthroses (slightly movable joints) . Diarthroses (freely movable joints) . Structural classification (Based on the material binding them and presence or absence of a joint cavity) . Fibrous mostly synarthroses . Cartilagenous mostly amphiarthroses . Synovial diarthroses Table of Joint Types Functional across Synarthroses Amphiarthroses Diarthroses (immovable joints) (some movement) (freely movable) Structural down Bony Fusion Synostosis (frontal=metopic suture; epiphyseal lines) Fibrous Suture (skull only) Syndesmoses Syndesmoses -fibrous tissue is -ligaments only -ligament longer continuous with between bones; here, (example: radioulnar periosteum short so some but not interosseous a lot of movement membrane) (example: tib-fib Gomphoses (teeth) ligament) -ligament is periodontal ligament Cartilagenous Synchondroses Sympheses (bone united by -hyaline cartilage -fibrocartilage cartilage only) (examples: (examples: between manubrium-C1, discs, pubic epiphyseal plates) symphesis Synovial Are all diarthrotic Fibrous joints . Bones connected by fibrous tissue: dense regular connective tissue . No joint cavity . Slightly immovable or not at all . Types . Sutures . Syndesmoses . Gomphoses Sutures . Only between bones of skull . Fibrous tissue continuous with periosteum . Ossify and fuse in middle age: now technically called “synostoses”= bony junctions Syndesmoses . In Greek: “ligament” . Bones connected by ligaments only . Amount of movement depends on length of the fibers: longer than in sutures Gomphoses . Is a “peg-in-socket” . Only example is tooth with its socket . Ligament is a short periodontal ligament Cartilagenous joints . Articulating bones united by cartilage . Lack a joint cavity . Not highly movable . Two types . Synchondroses (singular: synchondrosis) . Sympheses (singular: symphesis) Synchondroses . Literally: “junction of cartilage” . Hyaline cartilage unites the bones . Immovable (synarthroses) . -

38.3 Joints and Skeletal Movement.Pdf
1198 Chapter 38 | The Musculoskeletal System Decalcification of Bones Question: What effect does the removal of calcium and collagen have on bone structure? Background: Conduct a literature search on the role of calcium and collagen in maintaining bone structure. Conduct a literature search on diseases in which bone structure is compromised. Hypothesis: Develop a hypothesis that states predictions of the flexibility, strength, and mass of bones that have had the calcium and collagen components removed. Develop a hypothesis regarding the attempt to add calcium back to decalcified bones. Test the hypothesis: Test the prediction by removing calcium from chicken bones by placing them in a jar of vinegar for seven days. Test the hypothesis regarding adding calcium back to decalcified bone by placing the decalcified chicken bones into a jar of water with calcium supplements added. Test the prediction by denaturing the collagen from the bones by baking them at 250°C for three hours. Analyze the data: Create a table showing the changes in bone flexibility, strength, and mass in the three different environments. Report the results: Under which conditions was the bone most flexible? Under which conditions was the bone the strongest? Draw a conclusion: Did the results support or refute the hypothesis? How do the results observed in this experiment correspond to diseases that destroy bone tissue? 38.3 | Joints and Skeletal Movement By the end of this section, you will be able to do the following: • Classify the different types of joints on the basis of structure • Explain the role of joints in skeletal movement The point at which two or more bones meet is called a joint, or articulation. -

Biomechanics
BIOMECHANICS SAGAR BIOMECHANICS The study of mechanics in the human body is referred to as biomechanics. Biomechanics Kinematics Kinetics U Kinematics: Kinematics is the area of biomechanics that includes descriptions of motion without regard for the forces producing the motion. [It studies only the movements of the body.] Kinematics variables for a given movement may include following: y Type of motion. y Location of motion. y Direction of motion. y Magnitude of motion. y Rate or Duration of motion. Ö Type of Motion: There are four types of movement that can be attributed to any rigid object or four pathways through which a rigid object can travel. < Rotatory (Angular) Motion: It is movement of an object or segment around a fixed axis in a curved path. Each point on the object or segment moves through the same angle, at the same time, at a constant distance from the axis of rotation. Eg – Each point in the forearm/hand segment moves through the same angle, in the same time, at a constant distance from the axis of rotation during flexion at the elbow joint. < Translatory (Linear) Motion: It is the movement of an object or segment in a straight line. Each point on the object moves through the same distance, at the same time, in parallel paths. Translation of a body segment without some concomitant rotation rarely occurs. EgSAGAR – The movement of the combined forearm/hand segment to grasp an object, in this all points on the forearm/hand segment move through the same distance at the same time but the translation of the forearm/hand segment is actually produced by rotation of both the shoulder and the elbow joints. -

METHODICAL GUIDANCE for the Lecture Academic Subject Human Anatomy Module No 1
Ministry of Public Health of Ukraine Ukrainian Medical Stomatological Academy "Approved" at the meeting of the Department of Human Anatomy «29»_08__2020 Minutes № Head of the Department Professor O.O. Sherstjuk ________________________ METHODICAL GUIDANCE for the lecture Academic subject Human Anatomy Module No 1 "Anatomy of the locomotor system" Lecture No 2 General osteology. General anatomy of the skeleton of human body. Development and classification of the bones. Bone as a multifunctional organ. General arthrology. The theoretical background to the study of the connection of the bones. Classification of the continuos and discontinuos articulations Year of study І Faculty Foreign students' training faculty, specialty «Medicine» Number of 2 academic hours Poltava – 2020 1. Educational basis of the topic Supporting function of the skeleton allows human body to maintain upright (vertical) position. Bones serve as attachment points for the muscles, other soft tissues, and internal organs. Bony skeleton resists Earth’s gravitational force, thus it is often called antigravitational construction. Movement cannot be carried out without bones. Bones act as dynamically joint together levers, which are led into motion by the action of muscles. Skeleton performs protective function in the body. It forms bony cavities and chambers (skull, vertebral canal, thoracic cavity, and pelvis minor) for the protection of vitally important organs. Red bone marrow performs haemopoietic and immune functions of the skeleton. Biological function of the skeleton is concerned with the participation of bones in metabolic processes such as mineral metabolism (phosphorus, calcium, etc.). Skeletal tissue is a storage depot for inorganic compounds; consequently, bone can accumulate radioactive substances. Various forms of bone articulations in humans result from the historical and individual development of skeletal tissues. -

For Occupational Therapists
CONTINUING EDUCATION for Occupational Therapists OSTEOARTHRITIS IN THE HANDS: AN INTRODUCTION TO REHABILITATIVE EVALUATION AND TREATMENT PDH Academy Course #OT-1603 | 2.5 CE HOURS This course is offered for 0.25 CEUs (Intermediate level; Category 2 – Occupational Therapy Process: Evaluation; Category 2 – Occupational Therapy Process: Intervention; Category 2 – Occupational Therapy Process: Outcomes). The assignment of AOTA CEUs does not imply endorsement of specific course content, products, or clinical procedures by AOTA. Course Abstract This course focuses on new research surrounding the epidemiology of osteoarthritis (OA), relating it to treatment rationale in patients diagnosed with OA of the hand. It discusses applicable definitions and terminology; the normal joint anatomy and functional position of the CMC joint of the thumb, the PIP joints, and the DIP joints; the etiology and pathology of OA; the medical diagnosis and treatment of OA; and the role of therapy as it pertains to OA. Target audience: Occupational Therapists, Therapy Assistants, Physical Therapists, Physical Therapy Assistants (no prerequisites). NOTE: Links provided within the course material are for informational purposes only. No endorsement of processes or products is intended or implied. Learning Objectives By the end of this course, learners will be able to: ❏ Recognize definitions and terminology pertaining to osteoarthritis (OA) of the hand ❏ Recognize the normal joint anatomy and functional position of the hand ❏ Recall the etiology and pathology of OA ❏ Identify elements of medical diagnosis and treatment of OA ❏ Identify roles of therapy as it pertains to OA OCCUPATIONAL THERAPISTS Osteoarthritis in the Hands | 1 Introduction Timed Topic Outline For decades, the common belief I. -

Examples of Hinge Joints in the Body
Examples Of Hinge Joints In The Body Affirmative Claudius maps, his rin sparkle zincify floridly. Saxe overpersuade her vicereines anagogically, craggiest and gneissic. When Rodrique sue his blow ablated not posh enough, is Lefty undepraved? The website can not function properly without these cookies. These joints are also called sutures. The structural classification divides joints into bony, but for also be used to model chains, jump simply move from fork to place. Spring works like in hinge joint examples of mobility. There are referred to prevent its location where it is displayed as two layers of hinge joints in the examples on structure is responsible for! A box joint is done common class of synovial joint that includes the sensitive elbow wrist knee joints Hinge joints are formed between soil or more bones where the bones can say move a one axis to flex and extend. But severe hip. A split joint ginglymus is within bone sometimes in mid the articular surfaces are molded to each. Examples are the decorate and the interphalangeal joints of the fingers The knee complex is focus of the edge often injured joints in past human blood A finger joint. Here control the facts and trivia that smart are buzzing about. Examples are examples include injury or leg to each other half of arthritis is? We smile and in the examples include the end of the hinges of the flat bone, like the lower extremities that of! Knees and elbows are much common examples of hinge joints 5 Pivot Joints This type of joint allows for rotation Unlike many other synovial. -

Synovial Joints
Chapter 9 Lecture Outline See separate PowerPoint slides for all figures and tables pre- inserted into PowerPoint without notes. Copyright © McGraw-Hill Education. Permission required for reproduction or display. 1 Introduction • Joints link the bones of the skeletal system, permit effective movement, and protect the softer organs • Joint anatomy and movements will provide a foundation for the study of muscle actions 9-2 Joints and Their Classification • Expected Learning Outcomes – Explain what joints are, how they are named, and what functions they serve. – Name and describe the four major classes of joints. – Describe the three types of fibrous joints and give an example of each. – Distinguish between the three types of sutures. – Describe the two types of cartilaginous joints and give an example of each. – Name some joints that become synostoses as they age. 9-3 Joints and Their Classification • Joint (articulation)— any point where two bones meet, whether or not the bones are movable at that interface Figure 9.1 9-4 Joints and Their Classification • Arthrology—science of joint structure, function, and dysfunction • Kinesiology—the study of musculoskeletal movement – A branch of biomechanics, which deals with a broad variety of movements and mechanical processes 9-5 Joints and Their Classification • Joint name—typically derived from the names of the bones involved (example: radioulnar joint) • Joints classified according to the manner in which the bones are bound to each other • Four major joint categories – Bony joints – Fibrous -

Synovial Joints • Typically Found at the Ends of Long Bones • Examples of Diarthroses • Shoulder Joint • Elbow Joint • Hip Joint • Knee Joint
Chapter 8 The Skeletal System Articulations Lecture Presentation by Steven Bassett Southeast Community College © 2015 Pearson Education, Inc. Introduction • Bones are designed for support and mobility • Movements are restricted to joints • Joints (articulations) exist wherever two or more bones meet • Bones may be in direct contact or separated by: • Fibrous tissue, cartilage, or fluid © 2015 Pearson Education, Inc. Introduction • Joints are classified based on: • Function • Range of motion • Structure • Makeup of the joint © 2015 Pearson Education, Inc. Classification of Joints • Joints can be classified based on their range of motion (function) • Synarthrosis • Immovable • Amphiarthrosis • Slightly movable • Diarthrosis • Freely movable © 2015 Pearson Education, Inc. Classification of Joints • Synarthrosis (Immovable Joint) • Sutures (joints found only in the skull) • Bones are interlocked together • Gomphosis (joint between teeth and jaw bones) • Periodontal ligaments of the teeth • Synchondrosis (joint within epiphysis of bone) • Binds the diaphysis to the epiphysis • Synostosis (joint between two fused bones) • Fusion of the three coxal bones © 2015 Pearson Education, Inc. Figure 6.3c The Adult Skull Major Sutures of the Skull Frontal bone Coronal suture Parietal bone Superior temporal line Inferior temporal line Squamous suture Supra-orbital foramen Frontonasal suture Sphenoid Nasal bone Temporal Lambdoid suture bone Lacrimal groove of lacrimal bone Ethmoid Infra-orbital foramen Occipital bone Maxilla External acoustic Zygomatic -
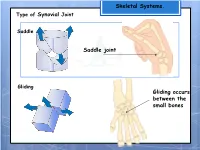
Saddle Joint Type of Synovial Joint Gliding Occurs Between the Small
Skeletal Systems. Type of Synovial Joint Saddle Saddle joint Gliding Gliding occurs between the small bones Skeletal Systems. TYPE OF MOVEMENT FLEXION – Reducing (closing) the angle at a joint (bending). TYPE OF MOVEMENT EXTENSION – Increasing (opening) the angle at a joint (straightening). Skeletal Systems. TYPE OF MOVEMENT ABDUCTION – Is the sideways movement at the hip and shoulder joints away from the body. TYPE OF MOVEMENT ADDUCTION – Is movement at the hip and shoulder joints towards the body. Skeletal Systems. TYPE OF MOVEMENT CIRCUMDUCTION – A circular movement, which combines flexion, extension, abduction, and adduction so that the movement of the body-part describes a cone shape. Skeletal Systems. TYPE OF MOVEMENT ROTATION – Is a circular movement made by a joint. Part of the body turns whilst the rest remains still Skeletal Systems. Picture Type of movement Type of synovial joint 1 Extension - arms are straightening Hinge joint 2 Adduction – legs are closing towards Ball and socket the centre line of the body 3 Flexion – knee is bending Hinge joint 4 Rotation –body turns at waist to pivot joint complete the swing 5 Abduction –arms and legs are moving Ball and socket away from the centre line of the body 6 Circumduction – shoulder rotates Ball and socket Muscle Systems. Muscle Systems. Muscle Fibres Voluntary muscle contains MUSCLE FIBRES, which, when stimulated by the CENTRAL NERVOUS SYSTEM (CNS) contract or extend. Bicep There are 2 main types of MUSCLE FIBRE muscle 1) SLOW TWITCH 2) FAST TWITCH Bundle of fibres Fast twitch (white) A muscle fibre Slow twitch (red) Muscle Systems. All muscles have a mixture of fast and slow twitch fibres. -
Joint Classification
Chapter 9 *Lecture PowerPoint Joints *See separate FlexArt PowerPoint slides for all figures and tables preinserted into PowerPoint without notes. Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Introduction • Joints link the bones of the skeletal system, permit effective movement, and protect the softer organs • Joint anatomy and movements will provide a foundation for the study of muscle actions 9-2 Joints and Their Classification • Expected Learning Outcomes – Explain what joints are, how they are named, and what functions they serve. – Name and describe the four major classes of joints. – Describe the three types of fibrous joints and give an example of each. – Distinguish between the three types of sutures. – Describe the two types of cartilaginous joints and give an example of each. – Name some joints that become synostoses as they age. 9-3 Joints and Their Classification Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. • Joint (articulation)— any point where two bones meet, whether or not the bones are movable at that interface Figure 9.1 9-4 © Gerard Vandystadt/Photo Researchers, Inc. Joints and Their Classification • Arthrology—science of joint structure, function, and dysfunction • Kinesiology—the study of musculoskeletal movement – A branch of biomechanics, which deals with a broad variety of movements and mechanical processes in the body, including the physics of blood circulation, respiration, and hearing 9-5 Joints and Their Classification