DOCSLIB.ORG

Interferometric Stellar Spectrometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Interferometric Stellar Spectrometry INTERFEROMETRIC STELLAR SPECTROMETRY by Ian Wynne Wynne-Jones Astronomy Group Blackett Laboratory, Imperial College, London SW7 2BZ Submitted to the University of London for the degree of Doctor of Philosophy London, December 1980 2 "Truth is the child of time, not of authority. dcwHnc^uk Our ignorance is infinite, so let us .diminition by a fraction. Why try to be so clever now, when at last we can become a little less stupid? I have had the unbelievable good fortune to lay my hands on a new instrument by means of which one can see one tiny corner of the universe a little clearer. Not much - but a little. Make use of it I " From The Life of Galileo By Bertolt Brecht. 3 ABSTRACT The theory of Fourier transform spectrometry is surveyed. The use of the Michelson interferometer for the Isaac Newton telescope is described. The instrument was used to study stellar spectra at high spectral resolution and high signal-to-noise ratio ^ 100 . The atmospheric motions of the luminous K stars, Arcturus, Hamal, Kochab and Pollux were studied. The profiles of their neutral iron absorption lines were measured and synthesized to obtain the microturbulent, macroturbulent and rotational velocities of their atmospheres. A Fourier technique was employed to dissect the line profiles, but it was concluded the method has no advantages compared with more traditional statistical tests. Evidence suggests a more realistic model for spectral line formation in turbulent media is required to synthesize the line profiles consistently. The hyperfine structures of the interstellar sodium D1 and D2 absorption lines in the directions of <X and S Cygni were observed for the first time. Synthesis of the profiles yielded velocity dispersions of *-250 ms ^ ,indicating diffuse interstellar cloud temperatures of 200°K and subsonic internal cloud motions. It was also concluded that the number density of interstellar clouds and variation of cloud column density was greater than previously thought. 4 ACKNOWLEDGEMENTS Firstly, I am indebted to Dr. R.C. Wayte for his guidance and example. I greatly appreciated the opportunity to learn from him and latterly, with him. Secondly, I am most grateful to Professor J. Ring for his supervision and constant encouragement. Thirdly, I would also like to thank Dr. A.P. Thome and Dr H.J. Walker for their constructive criticisms of the draft of this thesis. For their discussion and interest I am grateful to: Professor D. Blackwell, Professor D. Gray, Dr. R.Griffin, Professor B. Pagel, Dr. N.K Reay, Dr. M.A. Smith and Dr. S. Wychoff. To Professor J. Brault, Mr. C. Amos, Dr. K. Hartley, Mr. D. King and Dr. D. Youll I am thankful for advice on computing. I. should also like to thank members of staff and research students in the Astronomy Group at Imperial College and the Royal Greenwich Observatory, Herstmonceux for their help and friendship. Thanks also goes to Mrs. T. Wright for so patiently typing this thesis . X would like to acknowledge the PATT committee for their generous allocation of telescope time on the Isaac Newton telescope and to the Science Research Council for their financial support. Thanks is also due to the R.G.O. and I.C., computing and library sections for use of their resources. Finally, I should like to thank my parents, to whom I dedicate this thesis, for their understanding, and example of diligence and perseverance. 5 CONTENTS Page No CHAPTER 1 FOURIER TRANSFORM SPECTROMETRY 1.1 Introduction ^ 1.2 Theory of the interferogram ^ 1.3 Recovering the spectrum 1.4 The discretely sampled interferogram ^ 1.5 Discrete sampling restrictions ^0 1.6 Flux and acceptance ^4 1.7 Throughput and Luminosity ^9 6 97 1.8 Internal modulation ^ 1.9 Path difference errors 29 1.10 Demodulating the secondary interferogram JO 1.11 Sample interval measurement oJ/ 7 1.12 Interferogram sample signal-to-noise ratio ^7 CHAPTER 2 DATA REDUCTION OF INTERFEROGRAMS 2.1 Introduction 39 ,2.2 Theory 39 2.3 Spike elimination 41 2.4 Normalization of the spectra 48 2.5 The signal-to-noise ratio in the spectrum 50 2.6 Radial velocity measurements 53 CHAPTER 3 SYNTHESIS AND ANALYSIS OF STELLAR LINE PROFILES 3.1 Introduction 57 3.2 Line profile synthesis in local thermodynamic 58 equilibrium 3.2.1 Level populations 60 3.2.2 The absorption coefficient 61 3.2.3 Van der Waa^s broadening 63 6 Contents (Continued) Pa^e No 3.3 Radiative transfer 53 3.3.1 Flux integration gg 3.3.2 Continuous opacities gg 3.4 Model atmospheres gg 3.5 Macro turbulence 7^ 3.6 Rotation 72 3.7 Fourier analysis of line profiles 74 3.8 Macroturbulent and rotation filters 76 3.9 Synthetic line profiles 77 CHAPTER 4 STUDIES OF Fe I ABSORPTION IN LUMINOUS K STARS 4.1 Introduction gp 4.2 Selection of line profiles gg 4.3 Choice of star ^ 4.4 Analysis of line profile data 94 4.5 The Fourier analysis method 4.6 Results and discussion 4.6.1 Accuracy of profile measurements 4.6.2 Abundance and microturbulence ^24 4.6.3 Macroturbulence and rotation ^q 4.7 Conclusions 2.30 CHAPTER 5 INTERSTELLAR Na I D ABSORPTION LINE STUDIES 5.1 Introduction ^32 5.2 Interstellar absorption line profile synthesis ^34 5.3 Instrumental profile broadening ^35 5.4 Saturated line profiles ^3g 5.5 Synthesis of Na I D1 and D2 interstellar lines ^39 5.6 Observational data 7 Contents (Continued) Page No 5.7 Data Analysis 152 5.8 Results of model fitting 5.8.1 The °C Cygni sight line 153 5.8.2 The S Cygni sight line 169 5.8.3 The Tau sight line. 169 5.9 Discussion and comments. 175 8 TABLES 2.1 Number of spikes eliminated versus standard deviation. 47 3.1 Comparison of continuum opacities. 69 401 Atomic transition data of line profiles measured. 92 4.2 Stars observed. 95 4.3 Equivalent width grid for Fe I ^6151 X of Arcturus. 97 4.4 Mean square difference grids for Fe I ^6151 X of Arcturus. 98 4.5 Best fit parameters of line profiles. Ill 4.6 Average values for velocity parameters of each star. 112 4.7 Ratio of collisional to radiative ionization excitation rates 126 in the photosphere of a late type star. 4.8 Equivalent width verses ^29 5ol Atomic parameters used to synthesize Na I D1 and D2 lines. 141 5.2 Details of interstellar Na I D1 and D2 observing runs. 14$ 5.3 Stars observed for their insterstellar spectra. 151 5.4 Properties of well resolved interstellar components. 160 5.5 Seven cloud fit to o( Cygni line of sight. 160 5.6 Nine cloud fit to Cygni line of sight. 170 5.7 Model fits to S Cygni and At Tau. 176 9 FIGURES Page No 1.1 A schematic diagram of a Fourier Transform Spectrometer. 15 1.2 A discretely sampled interferogram instrumental profile. 21 1.3 A continuously sampled interferogram instrumental profile. 22 1.4 The output intensity for an off-axis ray. 25 1.5a Asymmetric instrumental profiles. 31 1.5b Asymmetric absorption profiles. 32 1.6 Internal modulation amplitude error. 35 2.1 An interferogram before spike elimination. 45 2.2 An interferogram after spike elimination. 46 2.3 A spectrum before normalisation 51 2.4 A spectrum after normalisation. 52 3.1 Specific intensity. 64 3.2 Line profile dependence on element abundance. 78 3.3 Line profile dependence on microturbulence. 80 3.4 Line profile dependence on rotation. 84 3.5 Line profile dependence on macroturbulence. 86 3.6 Rotation profile Fourier transform filter. 87 3.7 Macroturbulence profile Fourier transform filter. 88 4.1a The spectrum of Dubhe around ^6065 8. 93 4.1b The spectrum of Aldebaran around "A5379 8. 93 4.2 The Fe I ^6151- 8 line* ofr-Arcturus. 99 4.3a The Fe I ft6151 8 line of Arcturus. 101 4.3b The Fe I ft6151 8 line of Arcturus. 103 10 FIGURES (Continued) Page No. 4.4 The Fe I A6027 X profile of Arcturus. 106 4.5 The Fe I 7\6027 X profile transform of Arcturus. 107 4.6 The Fe I 7\6065 X profile of Arcturus. 108 4.7 The Fe I ft6151 X profile of Arcturus. 110 4.8 The Fe I ^5379 X profile of Hamal. 113 4.9 The Fe I TV 6027 X profile of Hamal. 114 4.10 The Fe I J\6065 X profile of Hamal. 115 4.11 The Fe I 7*6151 X profile of Hamal. 116 4.12 The Fe I ft5379 X profile of Kochab. 117 4.13 The Fe I ft 6027 X profile of Kochab. 118 4.14 The Fe I ft 6065 X profile of Ko chab. 119 4.15 The Fe I ft6151 X profile of Kochab. 120 4.16 The Fe I ft5379 X profile of Pollux. 121 4.17 The Fe I ft6027 X profile of Pollux. 122 4.18 The Fe I A60 65 X profile of Pollux. 123 4.19 Non-LTE Fe I A6151 X profile of Arcturus. 128 5.1 Synthetic interstellar Na I D1 lines for various velocity dispersions. 142 5.2 Synthetic interstellar Na I D1 lines for various column densities. 143 5.3 Instrumental broadening of an unsaturated line. 145 5.4 Instrumental broadening of a saturated line. 146 5.5 Resolving power verses profile accuracy. 147 5.6 The +lkm/s D1 line in Cygni: a) Gaussian velocity distribution, 155 b) exponential velocity distribution.
Load more

Recommended publications
  • BRAS Newsletter August 2013
    www.brastro.org August 2013 Next meeting Aug 12th 7:00PM at the HRPO Dark Site Observing Dates: Primary on Aug. 3rd, Secondary on Aug. 10th Photo credit: Saturn taken on 20” OGS + Orion Starshoot - Ben Toman 1 What's in this issue: PRESIDENT'S MESSAGE....................................................................................................................3 NOTES FROM THE VICE PRESIDENT ............................................................................................4 MESSAGE FROM THE HRPO …....................................................................................................5 MONTHLY OBSERVING NOTES ....................................................................................................6 OUTREACH CHAIRPERSON’S NOTES .........................................................................................13 MEMBERSHIP APPLICATION .......................................................................................................14 2 PRESIDENT'S MESSAGE Hi Everyone, I hope you’ve been having a great Summer so far and had luck beating the heat as much as possible. The weather sure hasn’t been cooperative for observing, though! First I have a pretty cool announcement. Thanks to the efforts of club member Walt Cooney, there are 5 newly named asteroids in the sky. (53256) Sinitiere - Named for former BRAS Treasurer Bob Sinitiere (74439) Brenden - Named for founding member Craig Brenden (85878) Guzik - Named for LSU professor T. Greg Guzik (101722) Pursell - Named for founding member Wally Pursell
    [Show full text]
  • A Handbook of Double Stars, with a Catalogue of Twelve Hundred
    The original of this bool< is in the Cornell University Library. There are no known copyright restrictions in the United States on the use of the text. http://www.archive.org/details/cu31924064295326 3 1924 064 295 326 Production Note Cornell University Library pro- duced this volume to replace the irreparably deteriorated original. It was scanned using Xerox soft- ware and equipment at 600 dots per inch resolution and com- pressed prior to storage using CCITT Group 4 compression. The digital data were used to create Cornell's replacement volume on paper that meets the ANSI Stand- ard Z39. 48-1984. The production of this volume was supported in part by the Commission on Pres- ervation and Access and the Xerox Corporation. Digital file copy- right by Cornell University Library 1991. HANDBOOK DOUBLE STARS. <-v6f'. — A HANDBOOK OF DOUBLE STARS, WITH A CATALOGUE OF TWELVE HUNDRED DOUBLE STARS AND EXTENSIVE LISTS OF MEASURES. With additional Notes bringing the Measures up to 1879, FOR THE USE OF AMATEURS. EDWD. CROSSLEY, F.R.A.S.; JOSEPH GLEDHILL, F.R.A.S., AND^^iMES Mt^'^I^SON, M.A., F.R.A.S. "The subject has already proved so extensive, and still ptomises so rich a harvest to those who are inclined to be diligent in the pursuit, that I cannot help inviting every lover of astronomy to join with me in observations that must inevitably lead to new discoveries." Sir Wm. Herschel. *' Stellae fixac, quae in ccelo conspiciuntur, sunt aut soles simplices, qualis sol noster, aut systemata ex binis vel interdum pluribus solibus peculiari nexu physico inter se junccis composita.
    [Show full text]
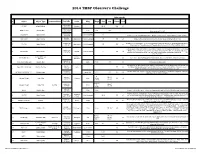
  • 2014 Observers Challenge List
    2014 TMSP Observer's Challenge Atlas page #s # Object Object Type Common Name RA, DEC Const Mag Mag.2 Size Sep. U2000 PSA 18h31m25s 1 IC 1287 Bright Nebula Scutum 20'.0 295 67 -10°47'45" 18h31m25s SAO 161569 Double Star 5.77 9.31 12.3” -10°47'45" Near center of IC 1287 18h33m28s NGC 6649 Open Cluster 8.9m Integrated 5' -10°24'10" Can be seen in 3/4d FOV with above. Brightest star is 13.2m. Approx 50 stars visible in Binos 18h28m 2 NGC 6633 Open Cluster Ophiuchus 4.6m integrated 27' 205 65 Visible in Binos and is about the size of a full Moon, brightest star is 7.6m +06°34' 17h46m18s 2x diameter of a full Moon. Try to view this cluster with your naked eye, binos, and a small scope. 3 IC 4665 Open Cluster Ophiuchus 4.2m Integrated 60' 203 65 +05º 43' Also check out “Tweedle-dee and Tweedle-dum to the east (IC 4756 and NGC 6633) A loose open cluster with a faint concentration of stars in a rich field, contains about 15-20 stars. 19h53m27s Brightest star is 9.8m, 5 stars 9-11m, remainder about 12-13m. This is a challenge obJect to 4 Harvard 20 Open Cluster Sagitta 7.7m integrated 6' 162 64 +18°19'12" improve your observation skills. Can you locate the miniature coathanger close by at 19h 37m 27s +19d? Constellation star Corona 5 Corona Borealis 55 Trace the 7 stars making up this constellation, observe and list the colors of each star asterism Borealis 15H 32' 55” Theta Corona Borealis Double Star 4.2m 6.6m .97” 55 Theta requires about 200x +31° 21' 32” The direction our Sun travels in our galaxy.
    [Show full text]
  • Milan Dimitrijevic Avgust.Qxd
    1. M. Platiša, M. Popović, M. Dimitrijević, N. Konjević: 1975, Z. Fur Natur- forsch. 30a, 212 [A 1].* 1. Griem, H. R.: 1975, Stark Broadening, Adv. Atom. Molec. Phys. 11, 331. 2. Platiša, M., Popović, M. V., Konjević, N.: 1975, Stark broadening of O II and O III lines, Astron. Astrophys. 45, 325. 3. Konjević, N., Wiese, W. L.: 1976, Experimental Stark widths and shifts for non-hydrogenic spectral lines of ionized atoms, J. Phys. Chem. Ref. Data 5, 259. 4. Hey, J. D.: 1977, On the Stark broadening of isolated lines of F (II) and Cl (III) by plasmas, JQSRT 18, 649. 5. Hey, J. D.: 1977, Estimates of Stark broadening of some Ar III and Ar IV lines, JQSRT 17, 729. 6. Hey, J. D.: Breger, P.: 1980, Stark broadening of isolated lines emitted by singly - ionized tin, JQSRT 23, 311. 7. Hey, J. D.: Breger, P.: 1981, Stark broadening of isolated ion lines by plas- mas: Application of theory, in Spectral Line Shapes I, ed. B. Wende, W. de Gruyter, 201. 8. Сыркин, М. И.: 1981, Расчеты электронного уширения спектральных линий в теории оптических свойств плазмы, Опт. Спектроск. 51, 778. 9. Wiese, W. L., Konjević, N.: 1982, Regularities and similarities in plasma broadened spectral line widths (Stark widths), JQSRT 28, 185. 10. Konjević, N., Pittman, T. P.: 1986, Stark broadening of spectral lines of ho- mologous, doubly ionized inert gases, JQSRT 35, 473. 11. Konjević, N., Pittman, T. P.: 1987, Stark broadening of spectral lines of ho- mologous, doubly - ionized inert gases, JQSRT 37, 311. 12. Бабин, С.
    [Show full text]
  • Binocular Double Star Logbook
    Astronomical League Binocular Double Star Club Logbook 1 Table of Contents Alpha Cassiopeiae 3 14 Canis Minoris Sh 251 (Oph) Psi 1 Piscium* F Hydrae Psi 1 & 2 Draconis* 37 Ceti Iota Cancri* 10 Σ2273 (Dra) Phi Cassiopeiae 27 Hydrae 40 & 41 Draconis* 93 (Rho) & 94 Piscium Tau 1 Hydrae 67 Ophiuchi 17 Chi Ceti 35 & 36 (Zeta) Leonis 39 Draconis 56 Andromedae 4 42 Leonis Minoris Epsilon 1 & 2 Lyrae* (U) 14 Arietis Σ1474 (Hya) Zeta 1 & 2 Lyrae* 59 Andromedae Alpha Ursae Majoris 11 Beta Lyrae* 15 Trianguli Delta Leonis Delta 1 & 2 Lyrae 33 Arietis 83 Leonis Theta Serpentis* 18 19 Tauri Tau Leonis 15 Aquilae 21 & 22 Tauri 5 93 Leonis OΣΣ178 (Aql) Eta Tauri 65 Ursae Majoris 28 Aquilae Phi Tauri 67 Ursae Majoris 12 6 (Alpha) & 8 Vul 62 Tauri 12 Comae Berenices Beta Cygni* Kappa 1 & 2 Tauri 17 Comae Berenices Epsilon Sagittae 19 Theta 1 & 2 Tauri 5 (Kappa) & 6 Draconis 54 Sagittarii 57 Persei 6 32 Camelopardalis* 16 Cygni 88 Tauri Σ1740 (Vir) 57 Aquilae Sigma 1 & 2 Tauri 79 (Zeta) & 80 Ursae Maj* 13 15 Sagittae Tau Tauri 70 Virginis Theta Sagittae 62 Eridani Iota Bootis* O1 (30 & 31) Cyg* 20 Beta Camelopardalis Σ1850 (Boo) 29 Cygni 11 & 12 Camelopardalis 7 Alpha Librae* Alpha 1 & 2 Capricorni* Delta Orionis* Delta Bootis* Beta 1 & 2 Capricorni* 42 & 45 Orionis Mu 1 & 2 Bootis* 14 75 Draconis Theta 2 Orionis* Omega 1 & 2 Scorpii Rho Capricorni Gamma Leporis* Kappa Herculis Omicron Capricorni 21 35 Camelopardalis ?? Nu Scorpii S 752 (Delphinus) 5 Lyncis 8 Nu 1 & 2 Coronae Borealis 48 Cygni Nu Geminorum Rho Ophiuchi 61 Cygni* 20 Geminorum 16 & 17 Draconis* 15 5 (Gamma) & 6 Equulei Zeta Geminorum 36 & 37 Herculis 79 Cygni h 3945 (CMa) Mu 1 & 2 Scorpii Mu Cygni 22 19 Lyncis* Zeta 1 & 2 Scorpii Epsilon Pegasi* Eta Canis Majoris 9 Σ133 (Her) Pi 1 & 2 Pegasi Δ 47 (CMa) 36 Ophiuchi* 33 Pegasi 64 & 65 Geminorum Nu 1 & 2 Draconis* 16 35 Pegasi Knt 4 (Pup) 53 Ophiuchi Delta Cephei* (U) The 28 stars with asterisks are also required for the regular AL Double Star Club.
    [Show full text]
  • Titles Promote Sustainable Initiatives
    Student Research Poster Symposium April 8, 2011 Villanova University Sigma Xi Research Poster Symposium, April 8, 2011 2 Proceedings of the 2011 Student Research Symposium April 8, 2011 Villanova Room Villanova University Villanova, PA 19085 USA Supported by: The Villanova Chapter of Sigma Xi, the Scientific Research Society Sigma Xi Research Poster Symposium, April 8, 2011 This volume is also available electronically on the Sigma Xi chapter’s website, http://www.csc.villanova.edu/~sigmaxi/ Sigma Xi Research Poster Symposium, April 8, 2011 4 Welcome from the Poster Symposium Organizers Welcome to the 2010 Villanova University Sigma Xi’s Student Research Poster Symposium! Sigma Xi is the international honor society for research scientists and engineers. The Villanova chapter of Sigma Xi is proud to sponsor this poster symposium event to recognize and celebrate the research work accomplished by our students, and to give students an opportunity to further develop their skills in communicating those accomplishments. This book contains abstracts of 56 contributed posters. Outstanding posters will be recognized in the form of poster awards. Many thanks to all students who contributed to this symposium. We gratefully acknowledge the dedicated poster judges who committed to evaluating the research posters and providing written feedback at the end of the symposium. Special thanks for their time and commitment to promoting research at Villanova University! Congratulations to all! Mirela Damian Sigma Xi Chapter President Anil Bamezai Sigma Xi Chapter President-Elect Sridhar Santhanam Sigma Xi Chapter Secretary-Treasurer Sigma Xi Research Poster Symposium, April 8, 2011 Table of Contents Astronomy and Astrophysics (5) Ultraviolet Spectral Synthesis of HgMn Stars.
    [Show full text]
  • Shears Ellard Gore
    John Ellard Gore: ‘of immensity and minuteness’1 Jeremy Shears John Ellard Gore FRAS, MRIA (1845−1910) was an Irish amateur astronomer and prolific author of popular astronomy books. His main observational interest was variable stars, of which he discovered several, and he served as the first Director of the BAA Variable Star Section. He was also interested in binary stars, leading him to calculate the orbital elements of many such systems. He demonstrated that the companion of Sirius, thought by many to be a dark body, was in fact self-luminous. In doing so he provided the first indication of the enormous density of what later became known as white dwarfs. Introduction were descended from Sir Paul Gore (1567−1629), who was born in London and went to Ireland in John Ellard Gore (1845−1910; Figure 1) was an 1602 as a commander of a troop of horse. In 1615 Irish amateur astronomer and prolific author of he became MP for Ballyshannon in County Don- popular astronomy books. His main observa- egal10 and in 1622 was created Baronet of tional interest was variable stars. He was an Magherabegg, also in Donegal.11 The Gore fam- original member of the British Astronomical ily seat was Manor Gore in Donegal. John Ellard Association in 1890 and shortly after was ap- Gore’s great grandfather, Arthur Saunders Gore pointed as the first Director of the Associa- (1734−1809), was the Second Earl of Arran and tion’s Variable Star Section (BAA VSS), which the Arran Islands. is the world’s longest established organisation John Ellard Gore had three brothers12 and a for the systematic observation of variable stars.
    [Show full text]
  • On the Application of Stark Broadening Data Determined with a Semiclassical Perturbation Approach
    Atoms 2014, 2, 357-377; doi:10.3390/atoms2030357 OPEN ACCESS atoms ISSN 2218-2004 www.mdpi.com/journal/atoms Article On the Application of Stark Broadening Data Determined with a Semiclassical Perturbation Approach Milan S. Dimitrijević 1,2,* and Sylvie Sahal-Bréchot 2 1 Astronomical Observatory, Volgina 7, 11060 Belgrade, Serbia 2 Laboratoire d'Etude du Rayonnement et de la Matière en Astrophysique, Observatoire de Paris, UMR CNRS 8112, UPMC, 5 Place Jules Janssen, 92195 Meudon Cedex, France; E-Mail: [email protected] (S.S.-B.) * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +381-64-297-8021; Fax: +381-11-2419-553. Received: 5 May 2014; in revised form: 20 June 2014 / Accepted: 16 July 2014 / Published: 7 August 2014 Abstract: The significance of Stark broadening data for problems in astrophysics, physics, as well as for technological plasmas is discussed and applications of Stark broadening parameters calculated using a semiclassical perturbation method are analyzed. Keywords: Stark broadening; isolated lines; impact approximation 1. Introduction Stark broadening parameters of neutral atom and ion lines are of interest for a number of problems in astrophysical, laboratory, laser produced, fusion or technological plasma investigations. Especially the development of space astronomy has enabled the collection of a huge amount of spectroscopic data of all kinds of celestial objects within various spectral ranges. Consequently, the atomic data for trace elements, which had not been
    [Show full text]
  • Explorethe Impact That Killed the Dinosaursp. 26
    EXPLORE the impact that killed the dinosaurs p. 26 DECEMBER 2016 The world’s best-selling astronomy magazine Understanding cannibal star systems p. 20 How moon dust will put a ring around Mars p. 46 Discover colorful star clusters p. 32 www.Astronomy.com AND MORE BONUS Vol. 44 Astronomy on Tap becomes a hit p. 58 ONLINE • CONTENT Issue 12 Meet the master of stellar vistas p. 52 CODE p. 3 iOptron’s new mount tested p. 62 ÛiÃÌÊÊÞÕÀÊiÞiÌ°°° ...and share the dividends for a lifetime. Tele Vue APO refractors earn a high yield of happy owners. 35 years of hand-building scopes with care and dedication is why we see comments like: “Thanks to all at Tele Vue for such wonderful products.” The care that goes into building every Tele Vue telescope is evident from the first time you focus an image. What goes unseen are the hours of work that led to that moment. Hand-fitted rack & pinion focusers must withstand 10lb. deflection testing along their travel, yet operate buttery-smooth, without gear lash or image TV-60 shift. Optics are fitted, spaced, and aligned using proprietary techniques to form breathtaking low-power views, spectacular high-power planetary performance, or stunning wide-field images. When you purchase a TV-76 Tele Vue telescope you’re not so much buying a telescope as acquiring a lifetime observing companion. Comments from recent warranty cards UÊ­/6Èä®ÊºÊV>ÌÊÌ >ÊÞÕÊiÕ} ÊvÀÊ«ÀÛ`}ÊiÊÜÌ ÊÃÕV ʵÕ>ÌÞtÊ/ ÃÊÃV«iÊÜÊ}ÛiÊiÊ>Êlifetime TV-85 of observing happiness.” —M.E.,Canada U­/6ÇȮʺ½ÛiÊÜ>Ìi`Ê>Ê/6ÊÃV«iÊvÀÊ{äÊÞi>ÀðÊ>ÞtÊ`]ʽÊÛiÀÜ ii`tÊLove, Love, Love Ìtt»p °°]" U­/6nx®ÊºPerfect form, perfect function, perfectÊÌiiÃV«i]Ê>`ÊÊ``½ÌÊ >ÛiÊÌÊÜ>ÌÊxÊÞi>ÀÃÊÌÊ}iÌÊÌt»p,° °]/8 U­/6nx®Êº/ >ÊÞÕÊvÀÊ>}ÊÃÕV Êbeautiful equipment available.
    [Show full text]
  • Astrophysics
    Publications of the Astronomical Institute rais-mf—ii«o of the Czechoslovak Academy of Sciences Publication No. 70 EUROPEAN REGIONAL ASTRONOMY MEETING OF THE IA U Praha, Czechoslovakia August 24-29, 1987 ASTROPHYSICS Edited by PETR HARMANEC Proceedings, Vol. 1987 Publications of the Astronomical Institute of the Czechoslovak Academy of Sciences Publication No. 70 EUROPEAN REGIONAL ASTRONOMY MEETING OF THE I A U 10 Praha, Czechoslovakia August 24-29, 1987 ASTROPHYSICS Edited by PETR HARMANEC Proceedings, Vol. 5 1 987 CHIEF EDITOR OF THE PROCEEDINGS: LUBOS PEREK Astronomical Institute of the Czechoslovak Academy of Sciences 251 65 Ondrejov, Czechoslovakia TABLE OF CONTENTS Preface HI Invited discourse 3.-C. Pecker: Fran Tycho Brahe to Prague 1987: The Ever Changing Universe 3 lorlishdp on rapid variability of single, binary and Multiple stars A. Baglln: Time Scales and Physical Processes Involved (Review Paper) 13 Part 1 : Early-type stars P. Koubsfty: Evidence of Rapid Variability in Early-Type Stars (Review Paper) 25 NSV. Filtertdn, D.B. Gies, C.T. Bolton: The Incidence cf Absorption Line Profile Variability Among 33 the 0 Stars (Contributed Paper) R.K. Prinja, I.D. Howarth: Variability In the Stellar Wind of 68 Cygni - Not "Shells" or "Puffs", 39 but Streams (Contributed Paper) H. Hubert, B. Dagostlnoz, A.M. Hubert, M. Floquet: Short-Time Scale Variability In Some Be Stars 45 (Contributed Paper) G. talker, S. Yang, C. McDowall, G. Fahlman: Analysis of Nonradial Oscillations of Rapidly Rotating 49 Delta Scuti Stars (Contributed Paper) C. Sterken: The Variability of the Runaway Star S3 Arietis (Contributed Paper) S3 C. Blanco, A.
    [Show full text]
  • 1903Aj 23 . . . 22K 22 the Asteojsomic Al
    22 THE ASTEOJSOMIC AL JOUENAL. Nos- 531-532 22K . Taking into account the smallness of the weights in- concerned. Through the use of these tables the positions . volved, the individual differences which make up the and motions of many stars not included in the present 23 groups in the preceding table agree^very well. catalogue can be brought into systematic harmony with it, and apparently without materially less accuracy for the in- dividual stars than could be reached by special compu- Tables of Systematic Correction for N2 and A. tations for these stars in conformity with the system of B. 1903AJ The results of the foregoing comparisons. have been This is especially true of the star-places computed by utilized to form tables of systematic corrections for ISr2, An, Dr. Auwers in the catalogues, Ai and As. As will be seen Ai and As. In right-ascension no distinction is necessary by reference to the catalogue the positions and motions of between the various catalogues published by Dr. Auwers, south polar stars taken from N2 agree better with the beginning with the Fundamental-G at alo g ; but in decli- results of this investigation than do those taken from As, nation the distinction between the northern, intermediate, which, in turn, are quoted from the Cape Catalogue for and southern catalogues must be preserved, so far as is 1890. SYSTEMATIC COBEECTIOEB : CEDEE OF DECLINATIONS. Eight-Ascensions ; Cokrections, ¿las and 100z//xtf. Declinations; Corrections, Æs and IOOzZ/x^. B — ISa B —A B —N2 B —An B —Ai âas 100 â[is âas 100 âgô âSs 100
    [Show full text]
  • Arxiv:0709.4613V2 [Astro-Ph] 16 Apr 2008 .Quirrenbach A
    Astronomy and Astrophysics Review manuscript No. (will be inserted by the editor) M. S. Cunha · C. Aerts · J. Christensen-Dalsgaard · A. Baglin · L. Bigot · T. M. Brown · C. Catala · O. L. Creevey · A. Domiciano de Souza · P. Eggenberger · P. J. V. Garcia · F. Grundahl · P. Kervella · D. W. Kurtz · P. Mathias · A. Miglio · M. J. P. F. G. Monteiro · G. Perrin · F. P. Pijpers · D. Pourbaix · A. Quirrenbach · K. Rousselet-Perraut · T. C. Teixeira · F. Th´evenin · M. J. Thompson Asteroseismology and interferometry Received: date M. S. Cunha and T. C. Teixeira Centro de Astrof´ısica da Universidade do Porto, Rua das Estrelas, 4150-762, Porto, Portugal. E-mail: [email protected] C. Aerts Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200 D, 3001 Leuven, Belgium; Afdeling Sterrenkunde, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands. J. Christensen-Dalsgaard and F. Grundahl Institut for Fysik og Astronomi, Aarhus Universitet, Aarhus, Denmark. A. Baglin and C. Catala and P. Kervella and G. Perrin LESIA, UMR CNRS 8109, Observatoire de Paris, France. L. Bigot and F. Th´evenin Observatoire de la Cˆote d’Azur, UMR 6202, BP 4229, F-06304, Nice Cedex 4, France. T. M. Brown Las Cumbres Observatory Inc., Goleta, CA 93117, USA. arXiv:0709.4613v2 [astro-ph] 16 Apr 2008 O. L. Creevey High Altitude Observatory, National Center for Atmospheric Research, Boulder, CO 80301, USA; Instituto de Astrofsica de Canarias, Tenerife, E-38200, Spain. A. Domiciano de Souza Max-Planck-Institut f¨ur Radioastronomie, Auf dem H¨ugel 69, 53121 Bonn, Ger- many. P. Eggenberger Observatoire de Gen`eve, 51 chemin des Maillettes, 1290 Sauverny, Switzerland; In- stitut d’Astrophysique et de G´eophysique de l’Universit´e de Li`ege All´ee du 6 Aoˆut, 17 B-4000 Li`ege, Belgium.
    [Show full text]