An Analysis of Mathematical Notations: for Better Or for Worse
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

500 Natural Sciences and Mathematics
500 500 Natural sciences and mathematics Natural sciences: sciences that deal with matter and energy, or with objects and processes observable in nature Class here interdisciplinary works on natural and applied sciences Class natural history in 508. Class scientific principles of a subject with the subject, plus notation 01 from Table 1, e.g., scientific principles of photography 770.1 For government policy on science, see 338.9; for applied sciences, see 600 See Manual at 231.7 vs. 213, 500, 576.8; also at 338.9 vs. 352.7, 500; also at 500 vs. 001 SUMMARY 500.2–.8 [Physical sciences, space sciences, groups of people] 501–509 Standard subdivisions and natural history 510 Mathematics 520 Astronomy and allied sciences 530 Physics 540 Chemistry and allied sciences 550 Earth sciences 560 Paleontology 570 Biology 580 Plants 590 Animals .2 Physical sciences For astronomy and allied sciences, see 520; for physics, see 530; for chemistry and allied sciences, see 540; for earth sciences, see 550 .5 Space sciences For astronomy, see 520; for earth sciences in other worlds, see 550. For space sciences aspects of a specific subject, see the subject, plus notation 091 from Table 1, e.g., chemical reactions in space 541.390919 See Manual at 520 vs. 500.5, 523.1, 530.1, 919.9 .8 Groups of people Add to base number 500.8 the numbers following —08 in notation 081–089 from Table 1, e.g., women in science 500.82 501 Philosophy and theory Class scientific method as a general research technique in 001.4; class scientific method applied in the natural sciences in 507.2 502 Miscellany 577 502 Dewey Decimal Classification 502 .8 Auxiliary techniques and procedures; apparatus, equipment, materials Including microscopy; microscopes; interdisciplinary works on microscopy Class stereology with compound microscopes, stereology with electron microscopes in 502; class interdisciplinary works on photomicrography in 778.3 For manufacture of microscopes, see 681. -

What's in a Name? the Matrix As an Introduction to Mathematics
St. John Fisher College Fisher Digital Publications Mathematical and Computing Sciences Faculty/Staff Publications Mathematical and Computing Sciences 9-2008 What's in a Name? The Matrix as an Introduction to Mathematics Kris H. Green St. John Fisher College, [email protected] Follow this and additional works at: https://fisherpub.sjfc.edu/math_facpub Part of the Mathematics Commons How has open access to Fisher Digital Publications benefited ou?y Publication Information Green, Kris H. (2008). "What's in a Name? The Matrix as an Introduction to Mathematics." Math Horizons 16.1, 18-21. Please note that the Publication Information provides general citation information and may not be appropriate for your discipline. To receive help in creating a citation based on your discipline, please visit http://libguides.sjfc.edu/citations. This document is posted at https://fisherpub.sjfc.edu/math_facpub/12 and is brought to you for free and open access by Fisher Digital Publications at St. John Fisher College. For more information, please contact [email protected]. What's in a Name? The Matrix as an Introduction to Mathematics Abstract In lieu of an abstract, here is the article's first paragraph: In my classes on the nature of scientific thought, I have often used the movie The Matrix to illustrate the nature of evidence and how it shapes the reality we perceive (or think we perceive). As a mathematician, I usually field questions elatedr to the movie whenever the subject of linear algebra arises, since this field is the study of matrices and their properties. So it is natural to ask, why does the movie title reference a mathematical object? Disciplines Mathematics Comments Article copyright 2008 by Math Horizons. -

The Matrix As an Introduction to Mathematics
St. John Fisher College Fisher Digital Publications Mathematical and Computing Sciences Faculty/Staff Publications Mathematical and Computing Sciences 2012 What's in a Name? The Matrix as an Introduction to Mathematics Kris H. Green St. John Fisher College, [email protected] Follow this and additional works at: https://fisherpub.sjfc.edu/math_facpub Part of the Mathematics Commons How has open access to Fisher Digital Publications benefited ou?y Publication Information Green, Kris H. (2012). "What's in a Name? The Matrix as an Introduction to Mathematics." Mathematics in Popular Culture: Essays on Appearances in Film, Fiction, Games, Television and Other Media , 44-54. Please note that the Publication Information provides general citation information and may not be appropriate for your discipline. To receive help in creating a citation based on your discipline, please visit http://libguides.sjfc.edu/citations. This document is posted at https://fisherpub.sjfc.edu/math_facpub/18 and is brought to you for free and open access by Fisher Digital Publications at St. John Fisher College. For more information, please contact [email protected]. What's in a Name? The Matrix as an Introduction to Mathematics Abstract In my classes on the nature of scientific thought, I have often used the movie The Matrix (1999) to illustrate how evidence shapes the reality we perceive (or think we perceive). As a mathematician and self-confessed science fiction fan, I usually field questionselated r to the movie whenever the subject of linear algebra arises, since this field is the study of matrices and their properties. So it is natural to ask, why does the movie title reference a mathematical object? Of course, there are many possible explanations for this, each of which probably contributed a little to the naming decision. -

Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J
Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J. Keely. All Rights Reserved. Mathematical expressions can be typed online in a number of ways including plain text, ASCII codes, HTML tags, or using an equation editor (see Writing Mathematical Notation Online for overview). If the application in which you are working does not have an equation editor built in, then a common option is to write expressions horizontally in plain text. In doing so you have to format the expressions very carefully using appropriately placed parentheses and accurate notation. This document provides examples and important cautions for writing mathematical expressions in plain text. Section 1. How to Write Exponents Just as on a graphing calculator, when writing in plain text the caret key ^ (above the 6 on a qwerty keyboard) means that an exponent follows. For example x2 would be written as x^2. Example 1a. 4xy23 would be written as 4 x^2 y^3 or with the multiplication mark as 4*x^2*y^3. Example 1b. With more than one item in the exponent you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x2n must be written as x^(2n) and NOT as x^2n. Writing x^2n means xn2 . Example 1c. When using the quotient rule of exponents you often have to perform subtraction within an exponent. In such cases you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x5 The middle step of ==xx52− 3 must be written as x^(5-2) and NOT as x^5-2 which means x5 − 2 . -
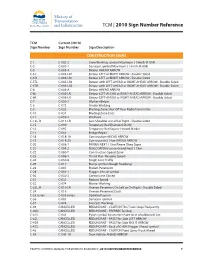
2010 Sign Number Reference for Traffic Control Manual
TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34 -
A New Rule-Based Method of Automatic Phonetic Notation On
A New Rule-based Method of Automatic Phonetic Notation on Polyphones ZHENG Min, CAI Lianhong (Department of Computer Science and Technology of Tsinghua University, Beijing, 100084) Email: [email protected], [email protected] Abstract: In this paper, a new rule-based method of automatic 2. A rule-based method on polyphones phonetic notation on the 220 polyphones whose appearing frequency exceeds 99% is proposed. Firstly, all the polyphones 2.1 Classify the polyphones beforehand in a sentence are classified beforehand. Secondly, rules are Although the number of polyphones is large, the extracted based on eight features. Lastly, automatic phonetic appearing frequency is widely discrepant. The statistic notation is applied according to the rules. The paper puts forward results in our experiment show: the accumulative a new concept of prosodic functional part of speech in order to frequency of the former 100 polyphones exceeds 93%, improve the numerous and complicated grammatical information. and the accumulative frequency of the former 180 The examples and results of this method are shown at the end of polyphones exceeds 97%. The distributing chart of this paper. Compared with other approaches dealt with polyphones’ accumulative frequency is shown in the polyphones, the results show that this new method improves the chart 3.1. In order to improve the accuracy of the accuracy of phonetic notation on polyphones. grapheme-phoneme conversion more, we classify the Keyword: grapheme-phoneme conversion; polyphone; prosodic 700 polyphones in the GB_2312 Chinese-character word; prosodic functional part of speech; feature extracting; system into three kinds in our text-to-speech system 1. -

Glossary of Linear Algebra Terms
INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w. -

Math Object Identifiers – Towards Research Data in Mathematics
Math Object Identifiers – Towards Research Data in Mathematics Michael Kohlhase Computer Science, FAU Erlangen-N¨urnberg Abstract. We propose to develop a system of “Math Object Identi- fiers” (MOIs: digital object identifiers for mathematical concepts, ob- jects, and models) and a process of registering them. These envisioned MOIs constitute a very lightweight form of semantic annotation that can support many knowledge-based workflows in mathematics, e.g. clas- sification of articles via the objects mentioned or object-based search. In essence MOIs are an enabling technology for Linked Open Data for mathematics and thus makes (parts of) the mathematical literature into mathematical research data. 1 Introduction The last years have seen a surge in interest in scaling computer support in scientific research by preserving, making accessible, and managing research data. For most subjects, research data consist in measurement or simulation data about the objects of study, ranging from subatomic particles via weather systems to galaxy clusters. Mathematics has largely been left untouched by this trend, since the objects of study – mathematical concepts, objects, and models – are by and large ab- stract and their properties and relations apply whole classes of objects. There are some exceptions to this, concrete integer sequences, finite groups, or ℓ-functions and modular form are collected and catalogued in mathematical data bases like the OEIS (Online Encyclopedia of Integer Sequences) [Inc; Slo12], the GAP Group libraries [GAP, Chap. 50], or the LMFDB (ℓ-Functions and Modular Forms Data Base) [LMFDB; Cre16]. Abstract mathematical structures like groups, manifolds, or probability dis- tributions can formalized – usually by definitions – in logical systems, and their relations expressed in form of theorems which can be proved in the logical sys- tems as well. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

The Recent Trademarking of Pi: a Troubling Precedent
The recent trademarking of Pi: a troubling precedent Jonathan M. Borwein∗ David H. Baileyy July 15, 2014 1 Background Intellectual property law is complex and varies from jurisdiction to jurisdiction, but, roughly speaking, creative works can be copyrighted, while inventions and processes can be patented, and brand names thence protected. In each case the intention is to protect the value of the owner's work or possession. For the most part mathematics is excluded by the Berne convention [1] of the World Intellectual Property Organization WIPO [12]. An unusual exception was the successful patenting of Gray codes in 1953 [3]. More usual was the carefully timed Pi Day 2012 dismissal [6] by a US judge of a copyright infringement suit regarding π, since \Pi is a non-copyrightable fact." We mathematicians have largely ignored patents and, to the degree we care at all, have been more concerned about copyright as described in the work of the International Mathematical Union's Committee on Electronic Information and Communication (CEIC) [2].1 But, as the following story indicates, it may now be time for mathematicians to start paying attention to patenting. 2 Pi period (π:) In January 2014, the U.S. Patent and Trademark Office granted Brooklyn artist Paul Ingrisano a trademark on his design \consisting of the Greek letter Pi, followed by a period." It should be noted here that there is nothing stylistic or in any way particular in Ingrisano's trademark | it is simply a standard Greek π letter, followed by a period. That's it | π period. No one doubts the enormous value of Apple's partly-eaten apple or the MacDonald's arch. -

1.3 Matrices and Matrix Operations 1.3.1 De…Nitions and Notation Matrices Are Yet Another Mathematical Object
20 CHAPTER 1. SYSTEMS OF LINEAR EQUATIONS AND MATRICES 1.3 Matrices and Matrix Operations 1.3.1 De…nitions and Notation Matrices are yet another mathematical object. Learning about matrices means learning what they are, how they are represented, the types of operations which can be performed on them, their properties and …nally their applications. De…nition 50 (matrix) 1. A matrix is a rectangular array of numbers. in which not only the value of the number is important but also its position in the array. 2. The numbers in the array are called the entries of the matrix. 3. The size of the matrix is described by the number of its rows and columns (always in this order). An m n matrix is a matrix which has m rows and n columns. 4. The elements (or the entries) of a matrix are generally enclosed in brack- ets, double-subscripting is used to index the elements. The …rst subscript always denote the row position, the second denotes the column position. For example a11 a12 ::: a1n a21 a22 ::: a2n A = 2 ::: ::: ::: ::: 3 (1.5) 6 ::: ::: ::: ::: 7 6 7 6 am1 am2 ::: amn 7 6 7 =4 [aij] , i = 1; 2; :::; m, j =5 1; 2; :::; n (1.6) Enclosing the general element aij in square brackets is another way of representing a matrix A . 5. When m = n , the matrix is said to be a square matrix. 6. The main diagonal in a square matrix contains the elements a11; a22; a33; ::: 7. A matrix is said to be upper triangular if all its entries below the main diagonal are 0. -

Rotation Matrix - Wikipedia, the Free Encyclopedia Page 1 of 22
Rotation matrix - Wikipedia, the free encyclopedia Page 1 of 22 Rotation matrix From Wikipedia, the free encyclopedia In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example the matrix rotates points in the xy -Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv (see below for details). In two and three dimensions, rotation matrices are among the simplest algebraic descriptions of rotations, and are used extensively for computations in geometry, physics, and computer graphics. Though most applications involve rotations in two or three dimensions, rotation matrices can be defined for n-dimensional space. Rotation matrices are always square, with real entries. Algebraically, a rotation matrix in n-dimensions is a n × n special orthogonal matrix, i.e. an orthogonal matrix whose determinant is 1: . The set of all rotation matrices forms a group, known as the rotation group or the special orthogonal group. It is a subset of the orthogonal group, which includes reflections and consists of all orthogonal matrices with determinant 1 or -1, and of the special linear group, which includes all volume-preserving transformations and consists of matrices with determinant 1. Contents 1 Rotations in two dimensions 1.1 Non-standard orientation