1 Priority Queues Based on Braun Trees 1 1.1 Introduction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Game Trees, Quad Trees and Heaps
CS 61B Game Trees, Quad Trees and Heaps Fall 2014 1 Heaps of fun R (a) Assume that we have a binary min-heap (smallest value on top) data structue called Heap that stores integers and has properly implemented insert and removeMin methods. Draw the heap and its corresponding array representation after each of the operations below: Heap h = new Heap(5); //Creates a min-heap with 5 as the root 5 5 h.insert(7); 5,7 5 / 7 h.insert(3); 3,7,5 3 /\ 7 5 h.insert(1); 1,3,5,7 1 /\ 3 5 / 7 h.insert(2); 1,2,5,7,3 1 /\ 2 5 /\ 7 3 h.removeMin(); 2,3,5,7 2 /\ 3 5 / 7 CS 61B, Fall 2014, Game Trees, Quad Trees and Heaps 1 h.removeMin(); 3,7,5 3 /\ 7 5 (b) Consider an array based min-heap with N elements. What is the worst case running time of each of the following operations if we ignore resizing? What is the worst case running time if we take into account resizing? What are the advantages of using an array based heap vs. using a BST-based heap? Insert O(log N) Find Min O(1) Remove Min O(log N) Accounting for resizing: Insert O(N) Find Min O(1) Remove Min O(N) Using a BST is not space-efficient. (c) Your friend Alyssa P. Hacker challenges you to quickly implement a max-heap data structure - "Hah! I’ll just use my min-heap implementation as a template", you think to yourself. -
Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
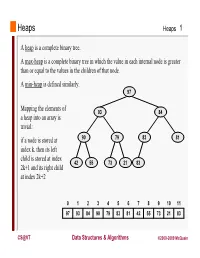
Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { . -

L11: Quadtrees CSE373, Winter 2020
L11: Quadtrees CSE373, Winter 2020 Quadtrees CSE 373 Winter 2020 Instructor: Hannah C. Tang Teaching Assistants: Aaron Johnston Ethan Knutson Nathan Lipiarski Amanda Park Farrell Fileas Sam Long Anish Velagapudi Howard Xiao Yifan Bai Brian Chan Jade Watkins Yuma Tou Elena Spasova Lea Quan L11: Quadtrees CSE373, Winter 2020 Announcements ❖ Homework 4: Heap is released and due Wednesday ▪ Hint: you will need an additional data structure to improve the runtime for changePriority(). It does not affect the correctness of your PQ at all. Please use a built-in Java collection instead of implementing your own. ▪ Hint: If you implemented a unittest that tested the exact thing the autograder described, you could run the autograder’s test in the debugger (and also not have to use your tokens). ❖ Please look at posted QuickCheck; we had a few corrections! 2 L11: Quadtrees CSE373, Winter 2020 Lecture Outline ❖ Heaps, cont.: Floyd’s buildHeap ❖ Review: Set/Map data structures and logarithmic runtimes ❖ Multi-dimensional Data ❖ Uniform and Recursive Partitioning ❖ Quadtrees 3 L11: Quadtrees CSE373, Winter 2020 Other Priority Queue Operations ❖ The two “primary” PQ operations are: ▪ removeMax() ▪ add() ❖ However, because PQs are used in so many algorithms there are three common-but-nonstandard operations: ▪ merge(): merge two PQs into a single PQ ▪ buildHeap(): reorder the elements of an array so that its contents can be interpreted as a valid binary heap ▪ changePriority(): change the priority of an item already in the heap 4 L11: Quadtrees CSE373, -

AVL Tree, Bayer Tree, Heap Summary of the Previous Lecture
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture • TREE is hierarchical (non linear) data structure • Binary trees • Definitions • Full tree, complete tree • Enumeration ( preorder, inorder, postorder ) • Binary search tree (BST) AVL tree The AVL tree (named for its inventors Adelson-Velskii and Landis published in their paper "An algorithm for the organization of information“ in 1962) should be viewed as a BST with the following additional property: - For every node, the heights of its left and right subtrees differ by at most 1. Difference of the subtrees height is named balanced factor. A node with balance factor 1, 0, or -1 is considered balanced. As long as the tree maintains this property, if the tree contains n nodes, then it has a depth of at most log2n. As a result, search for any node will cost log2n, and if the updates can be done in time proportional to the depth of the node inserted or deleted, then updates will also cost log2n, even in the worst case. AVL tree AVL tree Not AVL tree Realization of AVL tree element struct AVLnode { int data; AVLnode* left; AVLnode* right; int factor; // balance factor } Adding a new node Insert operation violates the AVL tree balance property. Prior to the insert operation, all nodes of the tree are balanced (i.e., the depths of the left and right subtrees for every node differ by at most one). After inserting the node with value 5, the nodes with values 7 and 24 are no longer balanced. -

Leftist Heap: Is a Binary Tree with the Normal Heap Ordering Property, but the Tree Is Not Balanced. in Fact It Attempts to Be Very Unbalanced!
Leftist heap: is a binary tree with the normal heap ordering property, but the tree is not balanced. In fact it attempts to be very unbalanced! Definition: the null path length npl(x) of node x is the length of the shortest path from x to a node without two children. The null path lengh of any node is 1 more than the minimum of the null path lengths of its children. (let npl(nil)=-1). Only the tree on the left is leftist. Null path lengths are shown in the nodes. Definition: the leftist heap property is that for every node x in the heap, the null path length of the left child is at least as large as that of the right child. This property biases the tree to get deep towards the left. It may generate very unbalanced trees, which facilitates merging! It also also means that the right path down a leftist heap is as short as any path in the heap. In fact, the right path in a leftist tree of N nodes contains at most lg(N+1) nodes. We perform all the work on this right path, which is guaranteed to be short. Merging on a leftist heap. (Notice that an insert can be considered as a merge of a one-node heap with a larger heap.) 1. (Magically and recursively) merge the heap with the larger root (6) with the right subheap (rooted at 8) of the heap with the smaller root, creating a leftist heap. Make this new heap the right child of the root (3) of h1. -

Data Structures and Programming Spring 2016, Final Exam
Data Structures and Programming Spring 2016, Final Exam. June 21, 2016 1 1. (15 pts) True or False? (Mark for True; × for False. Score = maxf0, Right - 2 Wrongg. No explanations are needed. (1) Let A1;A2, and A3 be three sorted arrays of n real numbers (all distinct). In the comparison model, constructing a balanced binary search tree of the set A1 [ A2 [ A3 requires Ω(n log n) time. × False (Merge A1;A2;A3 in linear time; then pick recursively the middle as root (in linear time).) (2) Let T be a complete binary tree with n nodes. Finding a path from the root of T to a given vertex v 2 T using breadth-first search takes O(log n) time. × False (Note that the tree is NOT a search tree.) (3) Given an unsorted array A[1:::n] of n integers, building a max-heap out of the elements of A can be performed asymptotically faster than building a red-black tree out of the elements of A. True (O(n) for building a max-heap; Ω(n log n) for building a red-black tree.) (4) In the worst case, a red-black tree insertion requires O(1) rotations. True (See class notes) (5) In the worst case, a red-black tree deletion requires O(1) node recolorings. × False (See class notes) (6) Building a binomial heap from an unsorted array A[1:::n] takes O(n) time. True (See class notes) (7) Insertion into an AVL tree asymptotically beats insertion into an AA-tree. × False (See class notes) (8) The subtree of the root of a red-black tree is always itself a red-black tree. -
Heapsort Previous Sorting Algorithms G G Heap Data Structure P Balanced
Previous sortinggg algorithms Insertion Sort 2 O(n ) time Heapsort Merge Sort Based off slides by: David Matuszek http://www.cis.upenn.edu/~matuszek/cit594-2008/ O(n) space PtdbMttBPresented by: Matt Boggus 2 Heap data structure Balanced binary trees Binary tree Recall: The dthfdepth of a no de iitditis its distance f rom th e root The depth of a tree is the depth of the deepest node Balanced A binary tree of depth n is balanced if all the nodes at depths 0 through n-2 have two children Left-justified n-2 (Max) Heap property: no node has a value greater n-1 than the value in its parent n Balanced Balanced Not balanced 3 4 Left-jjyustified binary trees Buildinggp up to heap sort How to build a heap A balanced binary tree of depth n is left- justified if: n it has 2 nodes at depth n (the tree is “full”)or ), or k How to maintain a heap it has 2 nodes at depth k, for all k < n, and all the leaves at dept h n are as fa r le ft as poss i ble How to use a heap to sort data Left-justified Not left-justified 5 6 The heappp prop erty siftUp A node has the heap property if the value in the Given a node that does not have the heap property, you can nodide is as large as or larger t han th e va lues iiin its give it the heap property by exchanging its value with the children value of the larger child 12 12 12 12 14 8 3 8 12 8 14 8 14 8 12 Blue node has Blue node has Blue node does not Blue node does not Blue node has heap property heap property have heap property have heap property heap property All leaf nodes automatically have -

Binary Heaps
Binary Heaps COL 106 Shweta Agrawal and Amit Kumar Revisiting FindMin • Application: Find the smallest ( or highest priority) item quickly – Operating system needs to schedule jobs according to priority instead of FIFO – Event simulation (bank customers arriving and departing, ordered according to when the event happened) – Find student with highest grade, employee with highest salary etc. 2 Priority Queue ADT • Priority Queue can efficiently do: – FindMin (and DeleteMin) – Insert • What if we use… – Lists: If sorted, what is the run time for Insert and FindMin? Unsorted? – Binary Search Trees: What is the run time for Insert and FindMin? – Hash Tables: What is the run time for Insert and FindMin? 3 Less flexibility More speed • Lists – If sorted: FindMin is O(1) but Insert is O(N) – If not sorted: Insert is O(1) but FindMin is O(N) • Balanced Binary Search Trees (BSTs) – Insert is O(log N) and FindMin is O(log N) • Hash Tables – Insert O(1) but no hope for FindMin • BSTs look good but… – BSTs are efficient for all Finds, not just FindMin – We only need FindMin 4 Better than a speeding BST • We can do better than Balanced Binary Search Trees? – Very limited requirements: Insert, FindMin, DeleteMin. The goals are: – FindMin is O(1) – Insert is O(log N) – DeleteMin is O(log N) 5 Binary Heaps • A binary heap is a binary tree (NOT a BST) that is: – Complete: the tree is completely filled except possibly the bottom level, which is filled from left to right – Satisfies the heap order property • every node is less than or equal to its children -

Lecture 13: AVL Trees and Binary Heaps
Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1.( ??) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally likely. static void shue(int[] arr) 2. Write a function that given the root of a binary search tree returns the node with the largest value. public static BSTNode<Integer> getLargest(BSTNode<Integer> root) 3. Explain how you would use a binary search tree to implement the Map ADT. We have included it below to remind you. Map.java //Stores a mapping of keys to values public interface Map<K,V> { //Adds key to the map with the associated value. If key already //exists, the associated value is replaced. void put(K key, V value); //Gets the value for the given key, or null if it isn't found. V get(K key); //Returns true if the key is in the map, or false otherwise. boolean containsKey(K key); //Removes the key from the map void remove(K key); //Number of keys in the map int size(); } What requirements must be placed on the Map? 4. Consider the following binary search tree. 10 5 15 1 12 18 16 17 1 Perform the following operations in order. (a) Remove 15. (b) Remove 10. (c) Add 13. (d) Add 8. 5. Suppose we begin with an empty BST. What order of add operations will yield the tallest possible tree? Review Solutions 1. One method (popular in programs like Excel) is to generate a random double corre- sponding to each element of the array, and then sort the array by the corresponding doubles. -

CMSC132 Summer 2017 Midterm 2
CMSC132 Summer 2017 Midterm 2 First Name (PRINT): ___________________________________________________ Last Name (PRINT): ___________________________________________________ I pledge on my honor that I have not given or received any unauthorized assistance on this examination. Your signature: _____________________________________________________________ Instructions · This exam is a closed-book and closed-notes exam. · Total point value is 100 points. · The exam is a 80 minutes exam. · Please use a pencil to complete the exam. · WRITE NEATLY. If we cannot understand your answer, we will not grade it (i.e., 0 credit). 1. Multiple Choice / 25 2. Short Answer / 45 3. Programming / 30 Total /100 1 1. [25 pts] Multiple Choice Identify the choice that best completes the statement or answers the question. Circle your answer. 1) [2] The cost of inserting or removing an element to/from a heap is log(N), where N is the total number of elements in the heap. The reason for that is: a) Heaps keep their entries sorted b) Heaps are balanced BST. c) Heaps are balanced binary trees. d) Heaps are a version of Red-Black trees 2) [2] What is the output of fun(2)? int fun(int n){ if (n == 4) return n; else return 2*fun(n+1); } a) 4 b) 8 c) 16 d) Runtime Error 3) [2] 2-3-4 Tree guarantees searching in ______________________time. a) O(log n) b) O (n) c) O (1) d) O (n log n) 4) [2] What is the advantage of an iterative method over a recursive one? a. It makes fewer calls b. It has less overhead c. It is easier to write, since you can use the method within itself. -

Merge Leftist Heaps Definition: Null Path Length
CSE 326: Data Structures New Heap Operation: Merge Given two heaps, merge them into one heap Priority Queues: – first attempt: insert each element of the smaller Leftist Heaps heap into the larger. runtime: Brian Curless Spring 2008 – second attempt: concatenate binary heaps’ arrays and run buildHeap. runtime: 1 2 Definition: Null Path Length Leftist Heaps null path length (npl) of a node x = the number of nodes between x and a null in its subtree OR Idea: npl(x) = min distance to a descendant with 0 or 1 children Focus all heap maintenance work in one • npl(null) = -1 small part of the heap • npl(leaf) = 0 • npl(single-child node) = 0 Leftist heaps: 1. Binary trees 2. Most nodes are on the left 3. All the merging work is done on the right Equivalent definition: 3 npl(x) = 1 + min{npl(left(x)), npl(right(x))} 4 Definition: Null Path Length Leftist Heap Properties Another useful definition: • Order property – parent’s priority value is ≤ to childrens’ priority npl(x) is the height of the largest perfect binary tree that is both values itself rooted at x and contained within the subtree rooted at x. –result: minimum element is at the root – (Same as binary heap) • Structure property – For every node x, npl(left(x)) ≥ npl(right(x)) –result: tree is at least as “heavy” on the left as the right (Terminology: we will say a leftist heap’s tree is a leftist 5 tree.) 6 2 Are These Leftist? 0 1 1 Observations 0 1 0 0 0 0 Are leftist trees always… 0 0 0 1 0 – complete? 0 0 1 – balanced? 2 0 00 0 1 1 0 Consider a subtree of a leftist tree… 0 1 0 0 0 0 – is it leftist? 0 0 0 0 7 Right Path in a Leftist Tree is Short (#1) Right Path in a Leftist Tree is Short (#2) Claim: The right path (path from root to rightmost Claim: If the right path has r nodes, then the tree has leaf) is as short as any in the tree. -

Binary Heaps
Binary Heaps CSE 373 Data Structures Readings • Chapter 8 › Section 8.3 Binary Heaps 2 BST implementation of a Priority Queue • Worst case (degenerate tree) › FindMin, DeleteMin and Insert (k) are all O(n) • Best case (completely balanced BST) › FindMin, DeleteMin and Insert (k) are all O(logn) • Balanced BSTs (next topic after heaps) › FindMin, DeleteMin and Insert (k) are all O(logn) Binary Heaps 3 Better than a speeding BST • We can do better than Balanced Binary Search Trees? › Very limited requirements: Insert, FindMin, DeleteMin. The goals are: › FindMin is O(1) › Insert is O(log N) › DeleteMin is O(log N) Binary Heaps 4 Binary Heaps • A binary heap is a binary tree (NOT a BST) that is: › Complete: the tree is completely filled except possibly the bottom level, which is filled from left to right › Satisfies the heap order property • every node is less than or equal to its children • or every node is greater than or equal to its children • The root node is always the smallest node › or the largest, depending on the heap order Binary Heaps 5 Heap order property • A heap provides limited ordering information • Each path is sorted, but the subtrees are not sorted relative to each other › A binary heap is NOT a binary search tree -1 2 1 0 1 4 6 2 6 0 7 5 8 4 7 These are all valid binary heaps (minimum) Binary Heaps 6 Binary Heap vs Binary Search Tree Binary Heap Binary Search Tree min value 5 94 10 94 10 97 min value 97 24 5 24 Parent is less than both Parent is greater than left left and right children child, less than right child Binary