Dynamics of Carving Runs in Alpine Skiing. II.Centrifugal Pendulum with a Retractable Leg
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
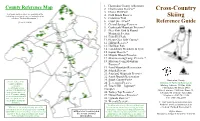
Cross-Country Skiing
1. Hunterdon County Arboretum County Reference Map 2. Charlestown Reserve* Cross-Country 3. Clover Hill Park Trail maps and brochures are available at the 4. Cold Brook Reserve Arboretum or online at www.co.hunterdon.nj.us Skiing (click on “Parks & Recreation”). 5. Columbia Trail (Revised 2/2020) 6. Court Street Park* Reference Guide 7. Crystal Springs Preserve 8. Cushetunk Mountain Preserve* 9. Deer Path Park & Round Mountain Section 10. Echo Hill Park 11. Heron Glen Golf Course* 12. Hilltop Reserve* 13. Hoffman Park 14. Landsdown Meadows & Trail 15. Laport Reserve* 16. Miquin Woods Preserve 17. Musconetcong Gorge Preserve* 18. Musconetcong Mountain Preserve* 19. Point Mountain Reservation 20. Schick Reserve 21. Sourland Mountain Preserve 22. South Branch Reservation 23. South County Park* Hunterdon County It is the policy of the County to provide 24. Teetertown Preserve Division of Parks & Recreation reasonable 25. Tower Hill—Jugtown* Mailing Address: PO Box 2900, accommodations to Flemington, NJ 08822-2900 persons with disabilities Complex Office Location: 1020 State Route 31, upon advance notice of 26. Turkey Top Preserve* Lebanon, NJ (Clinton Township) need. Persons requiring accommodations should 27. Union Furnace Preserve* Telephone: (908) 782-1158 make a request at least 2 28. Uplands Reserve* Fax: (908) 806-4057 weeks prior to program attendance. 29. Wescott Preserve E-mail: [email protected] The Hunterdon County Division of Parks and Website: www.co.hunterdon.nj.us With the exception of park properties with Recreation is dedicated to preserving open space (click on “Parks & Recreation”) reservable facilities, all properties are “carry in / and natural resources, providing safe parks and carry out” and trash/recycling receptacles are not *Skiing is not recommended. -

Physical Testing Characteristics and Technical Event Performance of Junior Alpine Ski Racers David Heikkinen
The University of Maine DigitalCommons@UMaine Electronic Theses and Dissertations Fogler Library 5-2003 Physical Testing Characteristics and Technical Event Performance of Junior Alpine Ski Racers David Heikkinen Follow this and additional works at: http://digitalcommons.library.umaine.edu/etd Part of the Kinesiology Commons Recommended Citation Heikkinen, David, "Physical Testing Characteristics and Technical Event Performance of Junior Alpine Ski Racers" (2003). Electronic Theses and Dissertations. 473. http://digitalcommons.library.umaine.edu/etd/473 This Open-Access Thesis is brought to you for free and open access by DigitalCommons@UMaine. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of DigitalCommons@UMaine. PHYSICAL TESTING CHARACTERISTICS AND TECHNICAL EVENT PERFORMANCE OF JUNIOR ALPINE SKI RACERS By David Heikkinen B.S. University of Maine at Farmington, 1998 A THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science (in Kinesiology and Physical Education) The Graduate School The University of Maine May, 2003 Advisory Committee: Robert Lehnhard, Associate Professor of Education, Advisor Phil Pratt, Cooperative Associate Education Stephen Butterfield, Professor of Education and Special Education PHYSICAL TESllNG CHARACTERlSllCS AND TECHNICAL EVENT PERFORNlANCE OF JUNIOR ALPlNE SKI RACERS By David Heikkinen Thesis Advisor: Dr. Robert Lehnhard An Abstract of the Thesis Presented in Partial Fulfillment of the Requirements for the Degree of Master of Science (in Kinesiology and Physical Education) May, 2003 The purpose of this study was to determine if a battery of physical tests can be used to distinguish between the ability levels of junior alpine ski racers. Many sports, such as football, have established laboratory and field tests to assess their athlete's preparation for competition. -

Freestyle/Freeskiing Competition Guide
Insurance isn’t one size fits all. At Liberty Mutual, we customize our policies to you, so you only pay for what you need. Home, auto and more, we’ll design the right policy, so you’re not left out in the cold. For more information, visit libertymutual.com. PROUD PARTNER Coverage provided and underwritten by Liberty Mutual Insurance and its affiliates, 175 Berkeley Street, Boston, MA 02116 USA. ©2018 Liberty Mutual Insurance. 2019 FREESTYLE / FREESKIING COMPETITION GUIDE On The Cover U.S. Ski Team members Madison Olsen and Aaron Blunck Editors Katie Fieguth, Sport Development Manager Abbi Nyberg, Sport Development Manager Managing Editor & Layout Jeff Weinman Cover Design Jonathan McFarland - U.S. Ski & Snowboard Creative Services Published by U.S. Ski & Snowboard Box 100 1 Victory Lane Park City, UT 84060 usskiandsnowboard.org Copyright 2018 by U.S. Ski & Snowboard. All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. Printed in the USA by RR Donnelley. Additional copies of this guide are available for $10.00, call 435.647.2666. 1 TABLE OF CONTENTS Key Contact Directory 4 Divisional Contacts 6 Chapter 1: Getting Started 9 Athletic Advancement 10 Where to Find More Information 11 Membership Categories 11 Code of Conduct 12 Athlete Safety 14 Parents 15 Insurance Coverage 16 Chapter 2: Points and Rankings 19 Event Scoring 20 Freestyle and Freeskiing Points List Calculations 23 Chapter 3: Competition 27 Age Class Competition 28 Junior Nationals 28 FIS Junior World Championships 30 U.S. -

Orienteering at Brighton Woods
ORIENTEERING AT BRIGHTON WOODS • There are eight numbered posts (controls) for the orienteering course at Brighton Woods. Each has a number that corresponds to the number on the Brighton Woods Orienteering Map, but they may be found in any order. • It is easier to go directly from control to control when there is less ground cover: late fall, winter, and early spring. Long pants are recommended because of the poison ivy and ticks. 1. NUMBERED CONTROL DESCRIPTIONS 1. Sports Field 2. Southwest End of Pipeline Clearing 3. Amphitheater 4. The Bridge 5. Head of Trail 6. Rock Outcropping 7. River 8. Northeast End of Pipeline Clearing 2. PLOTTING THE COURSE • Find control #1 on the map.(The Sports Field.) • On the map, line up one edge of the compass from where you are (Control #1: Sports Field) to where you want to go, (Control # 2: Southwest End of Pipeline Clearing) making sure the direction-of-travel arrow faces your destination point. (This is the first secret of orienteering.) • Rotate the housing of the compassso that the gridlines are parallel to the North - South gridlines on the orienteering map. The cardinal point N must be at the North side of your map. (This is the second secret to orienteering.) • Readyour bearing in degrees at the Bearing Index. (At the Direction-of- Travel line, or the "Read Bearing Here" mark.) The number of degrees is * • Do not rotate the housing again until you need a new bearing! 3. FINDING THE FIXED CONTROLS • Stand directly in front of the control #1 and hold your compass level and squarely in front of your body. -

Skiing and Snowboarding Injuries
SPORTS TIPS SKIING AND SNOWBOARDING INJURIES Tens of thousands of skiers and snowboarders enjoy snowsports every year, however few prepare for the rigorous physical demands that these sports place on the body. Although they can be safe sports, unexpected injuries may occur with improper preparation, varied snow conditions or poor judgment. Many injuries can be prevented by proper physical preparation, suitable and properly adjusted equipment, and common sense. WHAT CAUSES SKIING AND SNOWBOARDING INJURIES? Most snowsport injuries are traumatic, caused by being on dangerous terrain, lift accidents, falls, and collisions. In many instances, fatigue after a long day on the slopes or poor judgment can be blamed for injuries. The most common issues that predispose people to injury are: • Time skiing/snowboarding without rest • Skiing/snowboarding above ability level • Improper/faulty equipment • Inadequate adjustment to altitude • Dehydration/fatigue • Skiing/snowboarding off trail or in closed areas • Failure to observe posted warning signs by the mountain responsibility conduct code SKIING/SNOWBOARDING STOP SPORTS INJURIES — Keeping Kids in the Game for Life | www.STOPSportsInjuries.org What are some of the most common skiing/ Parental Oversight SNOWBOARDING INJURIES? Parents play an important role in educating their children about safe skiing and snowboarding practices. The wide range of skiing and snowboarding injuries They should help their children avoid terrain that involves many areas of the body, including: is beyond their ability and encourage professional • Anterior cruciate or collateral (ACL) ligament injuries instruction and routine rest breaks with rehydration. It • Shoulder dislocations or fractures is also important to caution children against improper • Shoulder separations speeds and the risks of skiing/snowboarding • Lower extremity fractures out-of-bounds. -

Fis Freestyle Skiing Judging Handbook
FIS FREESTYLE SKIING JUDGING HANDBOOK Edition October 2018 FIS Freestyle Skiing Judging Handbook October 2018 INTERNATIONAL SKI FEDERATION FEDERATION INTERNATIONALE DE SKI INTERNATIONALER SKI VERBAND Blochstrasse 2, CH- 3653 Oberhofen / Thunersee, Switzerland Telephone: +41 (33) 244 61 61 Fax: +41 (33) 244 61 71 Website: www.fis-ski.com Oberhofen, October 2018 Page 2 FIS Freestyle Skiing Judging Handbook October 2018 ‘We, the judges, promise to judge all competitions with complete impartiality; respecting and abiding by the rules and regulations. We promise to officiate at all competitions giving no favour based on nation, gender, competitor’s ranking, or previous performances in this or any other competition. We will judge each run solely on the merit of the observed performance without preconceptions or expectations.’ Page 3 FIS Freestyle Skiing Judging Handbook October 2018 Table of contents 6000 AERIALS........................................................................................................................ 5 6001 DEFINITION .................................................................................................................. 5 6002 SCORING ...................................................................................................................... 5 6002.1 AIR................................................................................................................................. 5 6002.2 FORM ........................................................................................................................... -

Skiing & Snowboarding Safety
Center for Injury Research and Policy The Research Institute at Nationwide Children’s Hospital Skiing & Snowboarding Safety Skiing and snowboarding are great ways to spend time outdoors during the winter months. As with all sports, injuries are a risk when you ski or snowboard. Taking a few safety measures can help you have fun and be safe. Skiing & Snowboarding Injury Facts Skiing & Snowboarding Safety Tips • Bruises and broken bones are the most common • Always wear a helmet designed for skiing or types of skiing- and snowboarding injuries. snowboarding. • Snowboarders most commonly injure their wrist • Protect your skin and eyes from the sun and and arm. Skiers most commonly injure their wind. Apply sunscreen and wear ski goggles that knee, head or face. fit properly with a helmet. • Most ski and snowboarding injuries occur during • Make sure your boots fit properly and bindings a fall or a crash (usually into a tree). are adjusted correctly. • Traumatic brain injury is the leading cause of • Prepare for the weather. Wear layers of clothes serious injuries among skiers and snowboarders and a helmet liner, a hat or a headband. and is also the most common cause of death. • Do not ski or snowboard alone. • Follow all trail rules. • Stay on the designated trails. Recommended Equipment • Only go on trails that match your skill level. • Helmet designed for skiing and snowboarding • Take a lesson – even experienced skiers and • Goggles that fit over a helmet snowboarders can benefit from a review. • Properly fitted boots and bindings • Before using a ski lift, tow rope or carpet, make • Sunscreen sure you know how to get on, ride and get off • Wrist guards for snowboarders safely. -

Cross Country Skiing
What You Should Know More Skiing Opportunities at other Kent County parks and trails Skiing is allowed if we have 4 inches or Cross Country more of snow on the ground. We only groom trails and rent Skiing When conditions are right for skiing, our skis at Palmer Park, but the Kent hours are 9:00 am to 5:00 pm. County parks shown below also offer scenic opportunities for skiing AT PALMER PARK There is a $2 trail fee per visit to help on ungroomed trails of varying cover the costs of grooming the trails, or difficulties. Note that our park skiers may purchase a season pass for $25. restrooms are unheated so We waive the trail fee if you rent our skis. they’re closed between November 1 and April 30 For current skiing conditions to prevent pipes from please call us at (616) 538-5050. freezing. At some parks, we open the gates and plow parking areas on Ski Rentals and Facilities weekdays but at others the gates are kept closed and lots are not maintained in the winter. The clubhouse at Kaufman Golf Course serves as Palmer Park’s hub for skiers. We rent skis and boots in all sizes for: Three 2-mile loops of groomed trails • $10 for adults • $8 for kids age 17 and younger, or Ski rentals at affordable rates • $30 for a family of up to five. Refreshments for sale and heated restrooms in the Clubhouse! We also offer light snacks and hot and cold beverages for sale. After exploring our wintery 335 acre park, you’ll also appreciate returning to the cozy fire often burning in our fireplace and our heated restrooms! Note that the clubhouse is accessed off Clyde Park Ave SW. -

2021-22 NYSEF Freeride Program Info
2021 - 2022 NYSEF Freeride Program We use the term Freeride to define the many disciplines within the sports of skiing and snowboarding not related to traditional nordic or alpine ski racing. Below are descriptions of each of the disciplines and some of the terminology used to describe each. Freestyle skiing – The foundation for what we call Freestyle skiing are the traditional sports of Moguls(M) and Aerials(A). The word “freestyle '' can also be used as a general term to describe snowboarding & skiing disciplines such as Halfpipe, Slopestyle, & Railjam which involves tricks, jumps, and terrain park features, such as rails, boxes, jibs, or other obstacles. Slopestyle (SS) – a judged skiing/snowboarding event held on a terrain-park course consisting of a variety of jumps, boxes, and rails. Skiercross (SX) – Also called Ski Cross. Downhill race with as many as six athletes in a heat on a course consisting of a variety of jumps, banked turns, and rollers. Athletes are normally seeded by way of an individual time trial prior to heat racing. The top athletes in each heat advance to the next round while the others are eliminated. Boardercross (BX) – Also called Snowboard Cross (SBX). Same as above with snowboarders. Railjam(RJ)(R) – Railjams are ski and/or snowboard events held solely on rails or box features in a jam-style format. In this format athletes take as many runs as possible in a predetermined time period and may or may not proceed to a final round. Can be judged by a panel of judges or by the competitors themselves. -

Performance Parameters in Competitive Alpine Skiing Disciplines of Slalom, Giant Slalom and Super-Giant Slalom
International Journal of Environmental Research and Public Health Article Performance Parameters in Competitive Alpine Skiing Disciplines of Slalom, Giant Slalom and Super-Giant Slalom Lidia B. Alejo 1,2 , Jaime Gil-Cabrera 1,3, Almudena Montalvo-Pérez 1 , David Barranco-Gil 1 , Jaime Hortal-Fondón 1 and Archit Navandar 1,* 1 Faculty of Sports Sciences, Universidad Europea de Madrid, C/Tajo, s/n, 28670 Madrid, Spain; [email protected] (L.B.A.); [email protected] (J.G.-C.); [email protected] (A.M.-P.); [email protected] (D.B.-G.); [email protected] (J.H.-F.) 2 Instituto de Investigación Hospital 12 de Octubre (imas12), 28041 Madrid, Spain 3 Royal Spanish Winter Sports Federation, 28703 San Sebastian de los Reyes, Spain * Correspondence: [email protected] Abstract: The objective of this study was to describe the kinematic patterns and impacts in male and female skiers in the super-giant slalom, giant slalom and slalom disciplines of an international alpine skiing competition using a portable Global Navigation Satellite Systems (GNSS) technology device. Fifteen skiers (males, n = 9, females, n = 6) volunteered to participate in this study. Data acquisition was carried out using a wireless inertial measurement device (WIMUTM PRO: hybrid location system GNSS at 18 Hz with a precision locator UltraWideband UWD (<10 cm) and 3D accelerometers 1000 Hz) where distances covered in different speed and acceleration thresholds and Citation: B. Alejo, L.; Gil-Cabrera, J.; impacts above 5g were recorded in each of the disciplines. Male and female alpine skiers showed Montalvo-Pérez, A.; Barranco-Gil, D.; different physical parameters and impacts even though they competed in the same courses in the Hortal-Fondón, J.; Navandar, A. -
Section B (A Technical Understanding of Snowboarding)
B/01 Section b - A Technical Understanding of Snowboarding 6 In this chapter we will explore... How snowboarders can alter their path down the The Snowboard mountain by making turns of different shapes and sizes. Alongside this, we will look at the different Turn phases of the turn which are particularly useful Turn Size and Shape when communicating the sequence of events throughout a turn to your Turn phases students. We will also explain the variety of turn types that can be used and Turn types consider the forces that impact the turn. Turn forces CHAPTER 6 / THE SNOWBOARD TURN B/02 Turn Size and Shape Put simply, the longer the board spends in the fall line or the more gradually a rider applies movements, the larger the turn becomes. When we define the size of the turn we consider the length and radius of the arc: small, medium or large. The size of your turn will vary depending on terrain, snow conditions and the type of turn you choose to make. SMALL MEDIUM LARGE A rider’s rate of descent down the mountain is controlled mainly by the shape of their turns relative to the fall line. The shape of these turns can be described as open (unfinished) and closed (finished). A closed turn is where the rider completes the turn across the hill, steering the snowboard perpendicular to the fall line. This type of turn will easily allow the rider to control both their forward momentum and rate of descent. Closed turns are used on steeper pitches, or firmer snow conditions, to keep forward momentum down. -

Instructor Guide
INSTRUCTOR GUIDE Using the CASI Rider Improvement Program (RIP) The CASI Rider Improvement Program (RIP) has been developed with the goal of being a flexible, adaptable program that is suitable for group lessons, private lessons, or multi-week programs. Feel free to adapt the program to your specific needs regarding duration, number of sessions, etc. Each progress card in the program provides some standard Program Stages: information: Students will progress their skills through the following stages, Info: from 1 through 5. Following the completion of stage 5, they may Student name, date, resort info, instructor name and final com- choose either the Freestylin’ or Freeridin’ stage (or they may ments: choose to complete both!). • This area is useful in creating return lessons, as it ensures that your students have a record of your lesson with them. • Comments should be overall positive with suggestions for I. LITTLE RIPPERS A future practice and skills. II. LITTLE RIPPERS B Terrain: The areas of the mountain that students can expect to use in this III. LITTLE RIPPERS C stage. 1. BASICS Goals: • These are the technical outcomes that you will work 2. TURNING towards during your time in the particular stage of the program. 3. CRUISING • Note: Depending on your program format, each stage may range from 1 – 3 lessons. For some students it may be 4. SHREDDING realistic to accomplish all of the goals in one lesson, but this will not be the norm. 5. RIPPING Skills – Technical: 6a. FREESTYLIN’ - and/or - 6b. FREERIDIN’ • These represent the technical points of the lesson that the instructor will be introducing and practicing with the student.