The Effect of Air Crashes on Plane Manufacturers Value. Abstract. The
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Download This Report
QUARTERLY · No 2 · AUGUST 2012 0 | P a g e Financial Derivatives Company Limited. Tel: 01-7739889 . Website: www.fdcng.com Copyright © 2012 by Financial Derivatives Company Ltd Publisher Financial Derivatives Company Limited Production Coordinator Areade Dare Editors Kathryn Stoneman Thessa Brongers-Bagu Cossana Preston Editorial Committee Mrs. Adefunke Adeyemi Capt. Adedapo Olumide Ms. Lola Adefope Mr. Dennis Eboremie Acknowledgments Damilola Akinbami Ayo Adesina 1 | P a g e Financial Derivatives Company Limited. Tel: 01-7739889 . Website: www.fdcng.com iPhone Wallpapers Front Cover images – Shutterstock, VectorsGraphic Dear Readers, Hello and welcome to the 2nd quarterly edition of Travelnomiks, the magazine for tourists, business travelers and aviation industry professionals. August has been a busy and exciting month worldwide, with the London Olympics dominating headlines. However, as the Olympics have now officially concluded and with Nigerian athletes returning home it is possible that we may now begin to wonder what the point of it all was; and, perhaps why we have all spent so many hours glued to our televisions! However, it is more important to recognize the overall message of the Olympics than to analyze Nigeria’s performance. As, the games are not just a celebration of sporting prowess, they are also an opportunity for the world to come together and to interact. They may also be the greatest visual manifestation of globalization. This visual manifestation is most poignantly expressed in the opening and closing ceremonies when the athletes assemble with their respective flags. During these events the athletes come together to celebrate both their triumphs and losses, and they are bound together through their participation. -

Punctuality Statistics Economic Regulation Group Aviation Data Unit
Punctuality Statistics Economic Regulation Group Aviation Data Unit Birmingham, Gatwick, Glasgow, Heathrow, Luton, Manchester, Stansted Full and Summary Analysis March 1996 Disclaimer The information contained in this report will be compiled from various sources and it will not be possible for the CAA to check and verify whether it is accurate and correct nor does the CAA undertake to do so. Consequently the CAA cannot accept any liability for any financial loss caused by the persons reliance on it. Contents Foreword Introductory Notes Full Analysis – By Reporting Airport Birmingham Edinburgh Gatwick Glasgow Heathrow London City Luton Manchester Newcastle Stansted Full Analysis With Arrival / Departure Split – By A Origin / Destination Airport B C – E F – H I – L M – N O – P Q – S T – U V – Z Summary Analysis FOREWORD 1 CONTENT 1.1 Punctuality Statistics: Heathrow, Gatwick, Manchester, Glasgow, Birmingham, Luton, Stansted, Edinburgh, Newcastle and London City - Full and Summary Analysis is prepared by the Civil Aviation Authority with the co-operation of the airport operators and Airport Coordination Ltd. Their assistance is gratefully acknowledged. 2 ENQUIRIES 2.1 Statistics Enquiries concerning the information in this publication and distribution enquiries concerning orders and subscriptions should be addressed to: Civil Aviation Authority Room K4 G3 Aviation Data Unit CAA House 45/59 Kingsway London WC2B 6TE Tel. 020-7453-6258 or 020-7453-6252 or email [email protected] 2.2 Enquiries concerning further analysis of punctuality or other UK civil aviation statistics should be addressed to: Tel: 020-7453-6258 or 020-7453-6252 or email [email protected] Please note that we are unable to publish statistics or provide ad hoc data extracts at lower than monthly aggregate level. -

Airliner Accident Statistics 2006
Airliner Accident Statistics 2006 Statistical summary of fatal multi-engine airliner accidents in 2006 Airliner Accident Statistics 2006 Statistical summary of world-wide fatal multi-engine airliner accidents in 2006 © Harro Ranter, the Aviation Safety Network January 1, 2007 this publication is available also on http://aviation-safety.net/pubs/ front page photo: non-fatal MD-10 accident at Memphis, December 18, 2003 © Dan Parent, kc10.net Airliner Accident Statistics 2006 2 CONTENTS CONTENTS .......................................................................................................... 3 SUMMARY ........................................................................................................... 4 0. SCOPE & DEFINITION ....................................................................................... 5 1. FATAL ACCIDENTS............................................................................................ 6 1.1 Fatal accidents summary........................................................................ 6 1.2 The year 2006 in historical perspective .................................................... 7 1.3 Regions ............................................................................................... 8 1.3.1 Accident location - countries ................................................................ 8 1.3.2 Accident location - regions................................................................. 10 1.3.3 Operator regions ............................................................................. -

Service Bulletin
Commercial Airplane 727 Group Service Bulletin Number: 727-57-0112 Revision Transmittal Sheet Date: September 2, 1970 Revision 5: July 31, 1997 ATA System: 5712 SUBJECT: WINGS - RIB UPPER CHORD AT BL 70.5 - INSPECTION, MODIFICATION, AND REPAIR This revision includes all pages of the service bulletin. COMPLIANCE INFORMATION RELATED TO THIS REVISION No more work is necessary on airplanes changed by Revision 4 of this service bulletin. More work is necessary on Group 1 airplanes changed by Revisions 2 or 3, Part V of the Accomplishment Instructions of this service bulletin. On Group 1 Airplanes with the Major Repair/Preventive Modification installed, it is necessary to make an inspection at BL 70.5 for a repair strap. If a strap is not installed, it is necessary to make an inspection of the frame for cracks. SUMMARY This revision is sent to tell operators that new kits are available for Group 1 and 2 Airplanes. The drawings used to install the kits are sent with this revision (the drawings have been revised since the release of Notice of Status Change 3). The format used to show the removal of parts and installation of the kits has changed. Also repairs, that operators have requested, are included, and the compliance information has been clarified. This revision is sent to tell the 727 airplane operators that this service bulletin has been identified by the 727 Structures Working Group (SWG), and the structural change and inspection given in this service bulletin are recommended to be included on applicable 727 airplanes. The change and inspection given in this service bulletin must be included at the times given in the Description and Accomplishment Instructions. -

Flying in the Face of Adversity (PDF of Layout)
BUSINESS XXXXXXXXXXAIRLINES The wreckage of a Nigerian airliner – which crashed just after take-off – lies in a field Flying In The in Abuja. Among the dead was the spiritual leader of Face of Adversity Muslims in Nigeria. Nick Ericsson assesses the state of Africa’s airline industry following the recent crashes in Nigeria Boeing 737 belonging to ADC AFRICA’S TEN WORST CRASHES of the many challenges facing an industry Airlines in Nigeria dropped with a critical image problem is that African- from the skies and crashed Location Airline Fatalities grown staff, at least those who can boast last October 29, and with it Morocco 1975 Alia 188 some measure of competence and profes- A Nigeria 1973 Nigerian Airways 176 what was left of the reputation and confi- sionalism, are increasingly being lured away dence in the country’s airline industry. The Niger 1989 UTA 171 by more established and wealthy carriers, loss of 96 lives – among them the spiritual Ivory Coast 2000 Kenya Airways 169 particularly from the Middle East. To remedy head of Nigeria’s 70 million Muslims, the Libya 1992 Libyan Arab Airlines 159 the problem, Afraa suggested that institu- sultan of Sokoto – followed soon after the Nigeria 1992 Nigerian Air Force 158 tions such as the African Development plane took off from the capital, Abuja. But Egypt 2004 Flash Airlines 148 Bank, as well as donor countries from the Nigeria 1996 ADC Airlines 143 the tragedy, the third in a year, has meant developed world, should provide funding Angola 1995 Trans Service Airlift 141 industry watchers are throwing their hands to establish skills training for the continent’s Benin 2003 UTA Guinea 141 up in collective exasperation at what they most under-resourced airlines to meet these see as typifying the state of much of the Source: Aviation Safety Network skills shortages. -

Airliner Census Western-Built Jet and Turboprop Airliners
World airliner census Western-built jet and turboprop airliners AEROSPATIALE (NORD) 262 7 Lufthansa (600R) 2 Biman Bangladesh Airlines (300) 4 Tarom (300) 2 Africa 3 MNG Airlines (B4) 2 China Eastern Airlines (200) 3 Turkish Airlines (THY) (200) 1 Equatorial Int’l Airlines (A) 1 MNG Airlines (B4 Freighter) 5 Emirates (300) 1 Turkish Airlines (THY) (300) 5 Int’l Trans Air Business (A) 1 MNG Airlines (F4) 3 Emirates (300F) 3 Turkish Airlines (THY) (300F) 1 Trans Service Airlift (B) 1 Monarch Airlines (600R) 4 Iran Air (200) 6 Uzbekistan Airways (300) 3 North/South America 4 Olympic Airlines (600R) 1 Iran Air (300) 2 White (300) 1 Aerolineas Sosa (A) 3 Onur Air (600R) 6 Iraqi Airways (300) (5) North/South America 81 RACSA (A) 1 Onur Air (B2) 1 Jordan Aviation (200) 1 Aerolineas Argentinas (300) 2 AEROSPATIALE (SUD) CARAVELLE 2 Onur Air (B4) 5 Jordan Aviation (300) 1 Air Transat (300) 11 Europe 2 Pan Air (B4 Freighter) 2 Kuwait Airways (300) 4 FedEx Express (200F) 49 WaltAir (10B) 1 Saga Airlines (B2) 1 Mahan Air (300) 2 FedEx Express (300) 7 WaltAir (11R) 1 TNT Airways (B4 Freighter) 4 Miat Mongolian Airlines (300) 1 FedEx Express (300F) 12 AIRBUS A300 408 (8) North/South America 166 (7) Pakistan Int’l Airlines (300) 12 AIRBUS A318-100 30 (48) Africa 14 Aero Union (B4 Freighter) 4 Royal Jordanian (300) 4 Europe 13 (9) Egyptair (600R) 1 American Airlines (600R) 34 Royal Jordanian (300F) 2 Air France 13 (5) Egyptair (600R Freighter) 1 ASTAR Air Cargo (B4 Freighter) 6 Yemenia (300) 4 Tarom (4) Egyptair (B4 Freighter) 2 Express.net Airlines -

© 2009 Sabre Inc. All Rights Reserved. [email protected]
© 2009 Sabre Inc. All rights reserved. [email protected] A Game-Winning Chess board photo by Shutterstock.com/Kit Sen Chin Background photo by Shutterstock.com/Sia Yambasu Plane photo by Danielle McLelland Addis AbabaS-based Ethiopian Airlines,tr which has continueda to buildte gy its network, expand its fleet and explore additional methods of earning revenue, is at the top of its game in Africa’s air travel market. By Christian Gossel | Ascend Contributor regional ince its first flight to Cairo, Egypt, in Airlines’ M&E division, a U.S. Federal Aviation ty will hold 104,000 tons per annum and will be April 1946, Ethiopian Airlines has steadily Administration-approved facility, has contrib- equipped with a modern 1,500-square-meter S expanded its network. The carrier began uted significantly to the airline’s bottom line, cold room designed to support a turnover of operations with five Douglas-McDonald DC-3s and to support its continued growth, the carrier 130 tons of palletized cargo per day. serving four routes in Egypt, Djibouti, Yemen will build a 7,200-square-meter state-of-the-art A combination of its continually expand- and Ethiopia. Today, it serves 44 international maintenance hangar that will accommodate ing network, increasing passenger traffic, destinations in Africa, Europe, the Middle East, two Boeing 767 aircraft concurrently. secondary revenue streams, forward-looking Asia and the United States with a fleet of 23 Cargo presents another important technology (such as Sabre® PC AirFlite™ flight aircraft. And, with 26 destinations in Africa, its source of revenue for the carrier. -

Yamoussoukro Decision
Public Disclosure Authorized DIRECTIONS IN DEVELOPMENT Public Disclosure Authorized Infrastructure Open Skies for Africa Implementing the Yamoussoukro Decision Charles E. Schlumberger Public Disclosure Authorized Public Disclosure Authorized Open Skies for Africa Open Skies for Africa Implementing the Yamoussoukro Decision Charles E. Schlumberger © 2010 The International Bank for Reconstruction and Development / The World Bank 1818 H Street, NW Washington, DC 20433 Telephone 202-473-1000 Internet www.worldbank.org E-mail [email protected] All rights reserved. 1 2 3 4 :: 13 12 11 10 This volume is a product of the staff of the International Bank for Reconstruction and Development / The World Bank. The findings, interpretations, and conclusions expressed in this volume do not necessarily reflect the views of the Executive Directors of The World Bank or the governments they represent. The World Bank does not guarantee the accuracy of the data included in this work. The bound- aries, colors, denominations, and other information shown on any map in this work do not imply any judgment on the part of The World Bank concerning the legal status of any territory or the endorsement or acceptance of such boundaries. Rights and Permissions The material in this publication is copyrighted. Copying and/or transmitting portions or all of this work without permission may be a violation of applicable law. The International Bank for Reconstruction and Development / The World Bank encourages dissemination of its work and will normally grant permission to reproduce portions of the work promptly. For permission to photocopy or reprint any part of this work, please send a request with complete information to the Copyright Clearance Center Inc., 222 Rosewood Drive, Danvers, MA 01923, USA; telephone: 978-750-8400; fax: 978-750-4470; Internet: www.copyright.com. -
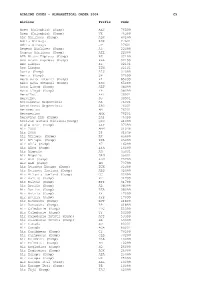
Airline Codes – Alphabetical Order 2004 C5
AIRLINE CODES – ALPHABETICAL ORDER 2004 C5 Airline Prefix Code Aces (Colombia) (Dump) AES 76599 Aces (Colombia) (Dump) VX 76599 ADC Airlines (Dump) ADK 40299 Adria Airways ADR 27601 Adria Airways JP 27601 Aegean Airlines (Dump) A3 22099 Aegean Airlines (Dump) AEE 22099 AER Arann Express (Dump) RE 02199 AER Arann Express (Dump) REA 02199 Aer Lingus EI 02101 Aer Lingus EIN 02101 Aeris (Dump) AIS 07099 Aeris (Dump) SH 07099 Aero Asia Internl (Dump) E4 65099 Aero Asia Internl (Dump) RSO 65099 Aero Lloyd (Dump) AEF 08099 Aero Lloyd (Dump) YP 08099 Aeroflot AFL 30901 Aeroflot SU 30901 Aerolineas Argentinas AR 76001 Aerolineas Argentinas ARG 76001 Aeromexico AM 76201 Aeromexico AMX 76201 Aerovias DAP (Dump) DAP 76499 African Safari Airlines(Dump) QSC 41099 Aigle Azur (Dump) AAF 07099 Air 2000 AMM 01048 Air 2000 DP 01048 Air Afrique (Dump) RK 45499 Air Afrique (Dump) RKA 45499 Air Alfa (Dump) H7 16099 Air Alfa (Dump) LFA 16099 Air Algerie AH 35001 Air Algerie DAH 35001 Air ALM (Dump) ALM 73799 Air ALM (Dump) LM 73799 Air Atlanta Europe (Dump) EUK 02099 Air Atlanta Iceland (Dump) ABD 02099 Air Atlanta Iceland (Dump) CC 02099 Air Baltic (Dump) BT 31799 Air Baltic (Dump) BTI 31799 Air Berlin (Dump) AB 08099 Air Berlin (Dump) BER 08099 Air Botnia (Dump) KF 17099 Air Botnia (Dump) KFB 17099 Air Botswana (Dump) BOT 41899 Air Botswana (Dump) BP 41899 Air Caledonie (Dump) TPC 53399 Air Caledonie (Dump) TY 53399 Air Caledonie Intntl (Dump) ACI 53399 Air Caledonie Intntl (Dump) SB 53399 Air Canada AC 80001 Air Canada ACA 80001 Air Caribbean (Dump) C2 70299 -
G:\JPH Section\ADU CODELIST\Codelist.Snp
Codelist Economic Regulation Group Aircraft By Name By CAA Code Airline By Name By CAA Code By Prefix Airport By Name By IATA Code By ICAO Code By CAA Code Codelist - Aircraft by Name Civil Aviation Authority Aircraft Name CAA code End Month AEROSPACELINES B377SUPER GUPPY 658 AEROSPATIALE (NORD)262 64 AEROSPATIALE AS322 SUPER PUMA (NTH SEA) 977 AEROSPATIALE AS332 SUPER PUMA (L1/L2) 976 AEROSPATIALE AS355 ECUREUIL 2 956 AEROSPATIALE CARAVELLE 10B/10R 388 AEROSPATIALE CARAVELLE 12 385 AEROSPATIALE CARAVELLE 6/6R 387 AEROSPATIALE CORVETTE 93 AEROSPATIALE SA315 LAMA 951 AEROSPATIALE SA318 ALOUETTE 908 AEROSPATIALE SA330 PUMA 973 AEROSPATIALE SA341 GAZELLE 943 AEROSPATIALE SA350 ECUREUIL 941 AEROSPATIALE SA365 DAUPHIN 975 AEROSPATIALE SA365 DAUPHIN/AMB 980 AGUSTA A109A / 109E 970 AGUSTA A139 971 AIRBUS A300 ( ALL FREIGHTER ) 684 AIRBUS A300-600 803 AIRBUS A300B1/B2 773 AIRBUS A300B4-100/200 683 AIRBUS A310-202 796 AIRBUS A310-300 775 AIRBUS A318 800 AIRBUS A319 804 AIRBUS A319 CJ (EXEC) 811 AIRBUS A320-100/200 805 AIRBUS A321 732 AIRBUS A330-200 801 AIRBUS A330-300 806 AIRBUS A340-200 808 AIRBUS A340-300 807 AIRBUS A340-500 809 AIRBUS A340-600 810 AIRBUS A380-800 812 AIRBUS A380-800F 813 AIRBUS HELICOPTERS EC175 969 AIRSHIP INDUSTRIES SKYSHIP 500 710 AIRSHIP INDUSTRIES SKYSHIP 600 711 ANTONOV 148/158 822 ANTONOV AN-12 347 ANTONOV AN-124 820 ANTONOV AN-225 MRIYA 821 ANTONOV AN-24 63 ANTONOV AN26B/32 345 ANTONOV AN72 / 74 647 ARMSTRONG WHITWORTH ARGOSY 349 ATR42-300 200 ATR42-500 201 ATR72 200/500/600 726 AUSTER MAJOR 10 AVIONS MUDRY CAP 10B 601 AVROLINER RJ100/115 212 AVROLINER RJ70 210 AVROLINER RJ85/QT 211 AW189 983 BAE (HS) 748 55 BAE 125 ( HS 125 ) 75 BAE 146-100 577 BAE 146-200/QT 578 BAE 146-300 727 BAE ATP 56 BAE JETSTREAM 31/32 340 BAE JETSTREAM 41 580 BAE NIMROD MR. -

THE IMPLEMENTATION of the YAMOUSSOUKRO DECISION By
THE IMPLEMENTATION OF THE YAMOUSSOUKRO DECISION By Charles E. Schlumberger Institute of Air and Space Law, Faculty of Law, McGill University, Montreal. February 2009 A thesis submitted to McGill University in partial fulfillment of the requirements of the degree of Doctor of Civil Law (DCL) © Charles E. Schlumberger, 2009 THE IMPLEMENTATION OF THE YAMOUSSOUKRO DECISION TABLE OF CONTENTS ACKNOWLEDGMENTS.............................................................................................................. v ABSTRACT ................................................................................................................................. viii RÉSUMÉ........................................................................................................................................ ix INTRODUCTION.......................................................................................................................... 1 CHAPTER 1 HISTORICAL BACKGROUND OF THE YAMOUSSOUKRO DECISION................................................................................................................................... 7 1.1 Early development of air services in Africa ....................................................................... 8 1.2 Post World War II era...................................................................................................... 13 CHAPTER 2 MAJOR ELEMENTS AND OBJECTIVES OF THE YAMOUSSOUKRO DECISION............................................................................................. 20 2.1 -

Use CTL/F to Search for INACTIVE Airlines on This Page - Airlinehistory.Co.Uk
The World's Airlines Use CTL/F to search for INACTIVE airlines on this page - airlinehistory.co.uk site search by freefind search Airline 1Time (1 Time) Dates Country A&A Holding 2004 - 2012 South_Africa A.T. & T (Aircraft Transport & Travel) 1981* - 1983 USA A.V. Roe 1919* - 1920 UK A/S Aero 1919 - 1920 UK A2B 1920 - 1920* Norway AAA Air Enterprises 2005 - 2006 UK AAC (African Air Carriers) 1979* - 1987 USA AAC (African Air Charter) 1983*- 1984 South_Africa AAI (Alaska Aeronautical Industries) 1976 - 1988 Zaire AAR Airlines 1954 - 1987 USA Aaron Airlines 1998* - 2005* Ukraine AAS (Atlantic Aviation Services) **** - **** Australia AB Airlines 2005* - 2006 Liberia ABA Air 1996 - 1999 UK AbaBeel Aviation 1996 - 2004 Czech_Republic Abaroa Airlines (Aerolineas Abaroa) 2004 - 2008 Sudan Abavia 1960^ - 1972 Bolivia Abbe Air Cargo 1996* - 2004 Georgia ABC Air Hungary 2001 - 2003 USA A-B-C Airlines 2005 - 2012 Hungary Aberdeen Airways 1965* - 1966 USA Aberdeen London Express 1989 - 1992 UK Aboriginal Air Services 1994 - 1995* UK Absaroka Airways 2000* - 2006 Australia ACA (Ancargo Air) 1994^ - 2012* USA AccessAir 2000 - 2000 Angola ACE (Aryan Cargo Express) 1999 - 2001 USA Ace Air Cargo Express 2010 - 2010 India Ace Air Cargo Express 1976 - 1982 USA ACE Freighters (Aviation Charter Enterprises) 1982 - 1989 USA ACE Scotland 1964 - 1966 UK ACE Transvalair (Air Charter Express & Air Executive) 1966 - 1966 UK ACEF Cargo 1984 - 1994 France ACES (Aerolineas Centrales de Colombia) 1998 - 2004* Portugal ACG (Air Cargo Germany) 1972 - 2003 Colombia ACI