Support of Icing Flight Tests with Near Real-Time Data Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

4Th QUARTER and FISCAL YEAR 2020
EMBRAER EARNINGS RESULTS th 4 QUARTER AND FISCAL YEAR 2020 HIGHLIGHTS • Embraer delivered 28 commercial jets and 43 executive jets (23 light / 20 large) in 4Q20, and in 2020 delivered 44 commercial jets and 86 executive jets (56 light / 30 large). Total company firm order backlog at the end of 2020 was US$ 14.4 billion; • Revenues in 4Q20 reached US$ 1,841.4 million and for fiscal year 2020 were US$ 3,771.1 million, representing year-over-year declines of 11.7% and 31.0%, respectively, versus their prior year periods; • Excluding special items, adjusted EBIT and EBITDA were US$ 76.6 million and US$ 145.6 million, respectively, yielding adjusted EBIT margin of 4.2% and adjusted EBITDA margin of 7.9%. For fiscal year 2020, adjusted EBIT was US$ (100.5) million (-2.7% margin) and adjusted EBITDA was US$ 82.1 million (2.2% margin), with the negative EBIT mostly driven by weakness in the Company’s Commercial Aviation segment within the context of the Covid-19 pandemic; • Adjusted net loss (excluding special items and deferred income tax and social contribution) in 4Q20 was US$ (12.5) million, with adjusted loss per ADS of US$ (0.07), while adjusted net loss for 2020 was US$ (463.7) million, with adjusted loss per ADS for the period of US$ (2.52); • Embraer reported a significant improvement in Free cash flow in 4Q20, reporting cash generation of US$ 725.1 million in the period, leading to full year free cash flow usage of US$ (990.2) million in 2020; • The Company finished the year with total cash of US$ 2.8 billion, steady versus the US$ 2.8 billion in cash at the end of 2019. -
Deliveries and Backlog Release
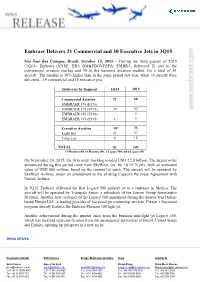
Embraer Delivers 21 Commercial and 30 Executive Jets in 3Q15 São José dos Campos, Brazil, October 15, 2015 – During the third quarter of 2015 (3Q15), Embraer (NYSE: ERJ; BM&FBOVESPA: EMBR3) delivered 21 jets to the commercial aviation market and 30 to the business aviation market, for a total of 51 aircraft. The number is 50% higher than in the same period last year, when 34 aircraft were delivered - 19 commercial and 15 executive jets. Deliveries by Segment 3Q15 2015 Commercial Aviation 21 68 EMBRAER 170 (E170) - - EMBRAER 175 (E175) 20 62 EMBRAER 190 (E190) - 3 EMBRAER 195 (E195) 1 3 Executive Aviation 30* 75 Light jets 21 57 Large jets 9 18 TOTAL 51 143 *3 Phenom 100, 18 Phenom 300 , 3 Legacy 500 and 6 Legacy 650 On September 30, 2015, the firm order backlog totaled USD 22.8 billion. The largest order announced during this period came from SkyWest, Inc. for 18 E175 jets, with an estimated value of USD 800 million, based on the current list price. The aircraft will be operated by SkyWest Airlines, under an amendment to the existing Capacity Purchase Agreement with United Airlines. In 3Q15, Embraer delivered the first Legacy 500 midsize jet to a customer in Mexico. The aircraft will be operated by Transpaís Aéreo, a subsidiary of the Lomex Group Aeronautics Division. Another new customer of the Legacy 500 announced during the quarter was Dallas- based Flexjet LLC, a leading provider of fractional jet ownership services. Flexjet’s fractional program already features the Embraer Phenom 300 light jet. Another achievement during the quarter came from the business mid-light jet Legacy 450, which has received type certification from the aeronautical authorities of Brazil, United States and Europe, opening up prospects in a new niche. -

The Best-Kept Secret of Successful Companies
SPECIAL ADVERTISING SECTION // BUSINESS AVIATION THE BEST-KEPT SECRET OF WRITTEN AND PRODUCED SUCCESSFUL COMPANIES BY MARK PATIKY Despite a vacillating U.S. economy, the need for a company With necessary cost cutting, slim management ranks and plane appears to be stronger than ever. What’s driving it? a lot more territory to cover, time is the currency of the new “When business in general takes a downturn, that’s the time economy. This has not gone unnoticed by the more than when you’ve got to get out and see people more frequently. 15,000 companies, entrepreneurs and individuals in the We’re doing that, we’re growing, and our business aircraft are U.S.—mostly small and midsize fi rms—that operate more a big part of that,” says Edmund O. Schweitzer III, President of than 23,000 business aircraft. These aircraft are essential Pullman, Wash.-based Schweitzer Engineering Laboratories. tools in today’s global economy. FLIGHT LOGS // REAL-LIFE BUSINESS AVIATION SUCCESS STORIES DR. TIRON MIKE KURT DANNY BURKE PECHET LEEDS CROSBY LAVY JONES Radiologist Former CEO, CEO, Crosby CEO, Elite Independent CMP Media Tugs LLC Group Inc. Real Estate Investor PAGE 3 PAGE 4 PAGE 6 PAGE 8 PAGE 10 ADVERTISEMENT 2 // THE ENLIGHTENED BUSINESS TRAVELER certainly won’t get there easily via airlines, which serve barely Your How-To Guide to 10% of these non-hub locations. It’s not only busy schedules that are driving the growth of a New World of Travel business aviation—it’s bottom-line results. A study of the S&P The Enlightened Business Traveler is your boarding pass to this 500 companies by Virginia-based consulting fi rm NEXA Advi- new world of travel. -

Boeing and Embraer Form J-V by Gregory Polek
PUBLICATIONS Vol.49 | No.8 $9.00 AUGUST 2018 | ainonline.com Orders flow at Farnborough As AIN went to press last month, airframers were raking in orders. The second day of the event continued the flurry of significant commercial airliner orders. The overall value totaled about $50 billion, taking the total value of new airliner contracts announced at the 2018 show close to $100 billion with a few trade days remaining. Aircraft Gulfstream G500 FAA certified page 6 Rotorcraft Fatigue fracture blamed in EC225 crash page 48 Pilot Report MARK WAGNER Avanti Evo delivers a smooth ride page 32 Boeing and Embraer form J-V by Gregory Polek Boeing will take an 80-percent share of annual pre-tax cost “synergies” of some Boeing CEO Dennis Muilenburg. “This Embraer’s commercial aviation business $150 million by its third year. important partnership clearly aligns with under the terms of a non-binding agree- The companies expect completion of Boeing’s long-term strategy of investing ment announced on July 5. The memo- the financial and operational details of the in organic growth and returning value to randum of understanding proposes the partnership and negotiation of transac- continues on page 9 formation of a joint venture meant to “stra- tion agreements to continue “in the com- tegically align” the companies’ commercial ing months.” The transaction would then Read Our SPECIAL REPORT development, production, marketing, and remain subject to shareholder and regu- lifecycle services operations. Under the latory approvals, including approval from terms of the agreement, Boeing will hold the government of Brazil. -

The Market for Business Jet Aircraft
The Market for Business Jet Aircraft Product Code #F613 A Special Focused Market Segment Analysis by: Civil Aircraft Forecast Analysis 3 The Market for Business Jet Aircraft 2010-2019 Table of Contents Executive Summary .................................................................................................................................................5 Figure 1 - The Market for Business Jet Aircraft By Market Segment - Units 2010 - 2019 (Bar Graph)...................................................................7 Figure 2 - The Market for Business Jet Aircraft By Market Segment - Values 2010 - 2019 (Bar Graph) ................................................................7 Figure 3 - The Market for Business Jet Aircraft By Market Segment - Units 2010 - 2019 (Pie Chart) ....................................................................8 Figure 4 - The Market for Business Jet Aircraft By Market Segment - Values 2010 - 2019 (Pie Chart)..................................................................8 Introduction................................................................................................................................................................9 Trends........................................................................................................................................................................11 Competitive Environment.....................................................................................................................................20 Table 1 - The Market -

Final Report No. 2205 by the Swiss Accident Investigation Board SAIB
Schweizerische Unfalluntersuchungsstelle SUST Service d’enquête suisse sur les accidents SESA Servizio d’inchiesta svizzero sugli infortuni SISI Swiss Accident Investigation Board SAIB Aviation Division Final Report No. 2205 by the Swiss Accident Investigation Board SAIB concerning the accident involving the Embraer EMB-505 aircraft, CN-MBR on 6 August 2012 St. Gallen-Altenrhein (LSZR) regional aerodrome, Thal/SG municipality Aéropôle 1, CH-1530 Payerne Tel. +41 26 662 33 00, Fax +41 26 662 33 01 [email protected] www.saib.admin.ch Final Report CN-MBR Ursachen Der Unfall ist darauf zurückzuführen, dass das Flugzeug nach einem unstabilisierten Endan- flug spät und mit zu hoher Geschwindigkeit auf der Piste aufsetzte und diese in der Folge überrollte. Zum Unfall beigetragen haben folgende Faktoren: Die mangelhafte Zusammenarbeit und die unzureichende Situationsanalyse durch die Besatzung. Die auf rund 10 Grad blockierten Landeklappen, was ungefähr der Klappenstellung 1 entsprach. Spätes Einleiten einer Vollbremsung nach der Landung. Swiss Accident Investigation Board page 2 of 90 Final Report CN-MBR General information on this report This report contains the Swiss Accident Investigation Board’s (SAIB) conclusions on the cir- cumstances and causes of the accident, which is the subject of the investigation. In accordance with Art 3.1 of the 10th edition, applicable from 18 November 2010, of Annex 13 to the Convention on International Civil Aviation of 7 December 1944 and Article 24 of the Federal Air Navigation Act, the sole purpose of the investigation of an aircraft accident or serious incident is to prevent accidents or serious incidents. The legal assessment of acci- dent and serious incidents causes and circumstances is expressly no concern of the accident investigation. -

Ground Handling Manual Luxaviation United Kingdom Revision 0 – 01/11/2019 © 2019 London Executive Aviation Ltd
Part GHM GROUND HANDLING MANUAL Section / Page Cover / 1 Rev. 0 Cover Date 01 / 11 / 19 Ground Handling Manual Luxaviation United Kingdom Revision 0 – 01/11/2019 © 2019 London Executive Aviation Ltd Part GHM GROUND HANDLING MANUAL Section / Page Cover / 2 Rev. 0 Cover Date 01 / 11 / 19 Intentionally Left Blank © 2019 London Executive Aviation Ltd Part GHM GROUND HANDLING MANUAL Section / Page Inc-Not / 1 Rev. 0 Incident Notification Date 01 / 11 / 19 Notification of Serious Incident or Accident The first person to become aware of an accident or incident to a Luxaviation UK must alert the company immediately. To notify London Executive Aviation (Luxaviation UK) of an accident, major incident, or security issue, please call: +44 (0) 1708 688420 When calling state: ➢ Who you are ➢ Where you are calling from ➢ Contact details ➢ Nature of incident (including brief details of incident, details regarding passengers, crew and aircraft status). To report any other incident involving a Luxaviation UK aircraft, please click here or scan the QR code below to access Luxaviation UK’s safety reporting system. To report an incident involving an aircraft from another Luxaviation or ExecuJet entity, please refer to 0.7.3 Luxaviation Group for contact details. © 2019 London Executive Aviation Ltd Part GHM GROUND HANDLING MANUAL Section / Page Inc-Not / 2 Rev. 0 Incident Notification Date 01 / 11 / 19 Intentionally Left Blank © 2019 London Executive Aviation Ltd Part GHM GROUND HANDLING MANUAL Section / Page Contents / 1 Rev. 0 Contents Date 01 / 11 / 19 Contents Notification of Serious Incident or Accident ........................................................................................... 1 Contents .................................................................................................................................................. 1 Section 0 – Administration and Control ................................................................................................. -

EMBRAER SA Form 6-K Current Event Report Filed
SECURITIES AND EXCHANGE COMMISSION FORM 6-K Current report of foreign issuer pursuant to Rules 13a-16 and 15d-16 Amendments Filing Date: 2019-10-21 | Period of Report: 2019-12-31 SEC Accession No. 0001292814-19-003481 (HTML Version on secdatabase.com) FILER EMBRAER S.A. Mailing Address Business Address AV. BRIGADEIRO FARIA AV. BRIGADEIRO FARIA CIK:1355444| IRS No.: 000000000 LIMA 2170 LIMA 2170 Type: 6-K | Act: 34 | File No.: 001-15102 | Film No.: 191159929 SAO JOSE DOS CAMPOS D5 SAO JOSE DOS CAMPOS D5 SIC: 3721 Aircraft 12227901 12227901 551239274404 Copyright © 2019 www.secdatabase.com. All Rights Reserved. Please Consider the Environment Before Printing This Document ____________________________________________________ UNITED STATES SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 _______________________ FORM 6-K __________________________________ Report of Foreign Private Issuer Pursuant to Rule 13a-16 or 15d-16 under the Securities Exchange Act of 1934 For the month of October 2019 Commission File Number: 001-15102 __________________________________ Embraer S.A. __________________________________ Av. Brigadeiro Faria Lima, 2170 12227-901 São José dos Campos, São Paulo, Brazil (Address of principal executive offices) __________________________________ Indicate by check mark whether the registrant files or will file annual reports under cover of Form 20-F or Form 40-F: Form 20-F x Form 40-F ¨ Indicate by check mark if the registrant is submitting the Form 6-K in paper as permitted by Regulation S-T Rule 101(b)(1): ¨ Indicate by check mark if the registrant is submitting the Form 6-K in paper as permitted by Regulation S-T Rule 101(b)(7): ¨ Copyright © 2019 www.secdatabase.com. -

BUSINESS Ciency and Higher Speed Than Competing Models
Honda HA-420 HondaJet Honda expects to receive certification of its $4.5 million light twin late this year. The HA-420 will have a range of 1,180 nm, a maximum speed of 420 knots, an initial climb rate of 4,000 fpm and a max- imum altitude of 43,000 feet. Honda claims the aircraft has greater fuel effi- BUSINESS ciency and higher speed than competing models. The four- to six-passenger jet will be certified for single-pilot operation. The HondaJet uses a carbon-fiber composite fuselage mated to metal wings. That, cou- pled with the unique positioning of the engines on over-the-wing pylons, reduces drag and creates a larger cabin volume JETS with generous passenger legroom and less by Mark Huber vibration. Honda expects most custom- ers to opt for a cabin configuration that Honda HA-420 HondaJet features a single-place, side-facing divan opposite the entry door followed by club- Cessna Citation M2 four seating and an aft-cabin lavatory The emerging ‘middle class’ with privacy door. Embraer Phenom 100E Key suppliers include GE Honda Aero Think less James Bond, more Cap- and inch dispatch rates even closer to Engines for the HF120 engines (2,050 tain Value. 100 percent. Development and certi- pounds of thrust each); Garmin for the New business jets under develop- fication schedules on select new pro- G3000 touchscreen avionics; and Emteq ment have one thing in common: with grams continue to fall behind because for its SkyPro HD IFE and cabin-man- a laser-like focus on value, almost to of specific financial challenges at agement system, which features audio/ the model they have achieved a near- select companies, technical difficul- Flaris LAR 01 video on demand, interactive 3-D moving MARK WAGNER perfect balance of versatility, perfor- ties integrating new technologies into map, exterior camera and wireless cabin mance, comfort and costs. -

New Aircraft Deliveries 2013
2013 Business Jet Forecast © Corporate Jet Investor 2013 1 2013 Business Jet Forecast Author: Alex Andrews Appendix: Terry Spruce Published May 2013 (2nd edition) Although Corporate Jet Investor has made every effort to ensure the accuracy of Corporate Jet Investor this report, neither it, or any contributor can accept any legal responsibility for Tranquil House consequences that may arise from errors or omissions or any opinions or advice Old Reigate Road given. This is not a substitute for professional advice on aircraft acquisitions, Betchworth financing or transactions. RH3 7DR United Kingdom All rights reserved. No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, T: +44 1737 844 383 recording or any information storage and retrieval system, without prior W: www.corporatejetinvestor.com permission in writing from the publisher. E: [email protected] © Corporate Jet Investor 2013 2 Executive Summary 2013 will be the fifth year in a row where total deliveries have fallen The business jet market has never had such a long drawn-out downturn. In 2013, manufacturers will deliver 44% less aircraft units than they did in 2008. If Hawker was still building jets and Cessna had not cut production, deliveries would have been similar to 2012. The large jet market is stronger but not back to its peak Over 80% of Gulfstream orders in 2013 will be for large-cabin jets. But it is worth noting that large aircraft deliveries are still down – even with the G650 coming on line. The light jet market is suffering badly Cessna is cutting production, Learjet prices are falling. -

Embraer Delivers 21 Commercial and 30 Executive Jets in 3Q15
Embraer Delivers 21 Commercial and 30 Executive Jets in 3Q15 São José dos Campos, Brazil, October 15, 2015 – During the third quarter of 2015 (3Q15), Embraer (NYSE: ERJ; BM&FBOVESPA: EMBR3) delivered 21 jets to the commercial aviation market and 30 to the business aviation market, for a total of 51 aircraft. The number is 50% higher than in the same period last year, when 34 aircraft were delivered - 19 commercial and 15 executive jets. Deliveries by Segment 3Q15 2015 Commercial Aviation 21 68 EMBRAER 170 (E170) - - EMBRAER 175 (E175) 20 62 EMBRAER 190 (E190) - 3 EMBRAER 195 (E195) 1 3 Executive Aviation 30* 75 Light jets 21 57 Large jets 9 18 TOTAL 51 143 *3 Phenom 100, 18 Phenom 300 , 3 Legacy 500 and 6 Legacy 650 On September 30, 2015, the firm order backlog totaled USD 22.1 billion. The largest order announced during this period came from SkyWest, Inc. for 18 E175 jets, with an estimated value of USD 800 million, based on the current list price. The aircraft will be operated by SkyWest Airlines, under an amendment to the existing Capacity Purchase Agreement with United Airlines. In 3Q15, Embraer delivered the first Legacy 500 midsize jet to a customer in Mexico. The aircraft will be operated by Transpaís Aéreo, a subsidiary of the Lomex Group Aeronautics Division. Another new customer of the Legacy 500 announced during the quarter was Dallas- based Flexjet LLC, a leading provider of fractional jet ownership services. Flexjet’s fractional program already features the Embraer Phenom 300 light jet. Another achievement during the quarter came from the business mid-light jet Legacy 450, which has received type certification from the aeronautical authorities of Brazil, United States and Europe, opening up prospects in a new niche. -

2017 Flexjet Media Kit Flexjet Media Kit 2
2017 FLEXJET MEDIA KIT FLEXJET MEDIA KIT 2 FLEXJET QUICK FACTS Website: www.flexjet.com Twitter: @Flexjet Founded: 1995 Chairman: Kenn Ricci CEO: Michael Silvestro Headquarters: Cleveland, Ohio Ownership: Privately held CURRENT PROGRAMS FRACTIONAL OWNERSHIP www.flexjet.com/programs/fractional-jet-ownership LEASE www.flexjet.com/programs/lease-option FLEXJET 25™ JET CARD www.flexjet.com/programs/jet-card FLEXJET MEDIA KIT ABOUT FLEXJET Launched on May 15, 1995 as a venture of Bombardier Aerospace Group and AMR Combs division of AMR Corp (the parent company of American Airlines), Flexjet LLC was founded at the dawn of the fractional aircraft industry “to provide affordable access to an increasingly important competitive tool – the business jet – to a much broader range of companies and individuals.” Flexjet was acquired in 2013 by Directional Aviation (www.directionalaviation.com), led by visionary aviation entrepreneur Kenn Ricci. Flexjet joined other companies in Directional Aviation’s $1 billion portfolio including Flight Options, Sentient Jet and Skyjet. Mr. Ricci realigned the vision of Flexjet, focusing it on the luxury fractional ownership experience, and steering it on a course toward becoming a leading luxury brand known for world-class service while committing to investments in new aircraft, facilities and technology. As it celebrated the 20th anniversary of its founding in 2015, Flexjet has fulfilled its initial promise, becoming one of the world’s leading providers of private jet travel. 4 FLEXJET MEDIA KIT 20 YEARS OF AERONAUTICAL