Conductive Casi2 Transparent in the Near Infra-Red Range Journal Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Seymur Cahangirov Hasan Sahin Guy Le Lay Angel Rubio Introduction to the Physics of Silicene and Other 2D Materials Lecture Notes in Physics
Lecture Notes in Physics 930 Seymur Cahangirov Hasan Sahin Guy Le Lay Angel Rubio Introduction to the Physics of Silicene and other 2D Materials Lecture Notes in Physics Volume 930 Founding Editors W. Beiglböck J. Ehlers K. Hepp H. Weidenmöller Editorial Board M. Bartelmann, Heidelberg, Germany B.-G. Englert, Singapore, Singapore P. Hanggi,R Augsburg, Germany M. Hjorth-Jensen, Oslo, Norway R.A.L. Jones, Sheffield, UK M. Lewenstein, Barcelona, Spain H. von Lohneysen,R Karlsruhe, Germany J.-M. Raimond, Paris, France A. Rubio, Hamburg, Germany M. Salmhofer, Heidelberg, Germany W. Schleich, Ulm, Germany S. Theisen, Potsdam, Germany D. Vollhardt, Augsburg, Germany J.D. Wells, Ann Arbor, USA G.P. Zank, Huntsville, USA [email protected] The Lecture Notes in Physics The series Lecture Notes in Physics (LNP), founded in 1969, reports new devel- opments in physics research and teaching-quickly and informally, but with a high quality and the explicit aim to summarize and communicate current knowledge in an accessible way. Books published in this series are conceived as bridging material between advanced graduate textbooks and the forefront of research and to serve three purposes: • to be a compact and modern up-to-date source of reference on a well-defined topic • to serve as an accessible introduction to the field to postgraduate students and nonspecialist researchers from related areas • to be a source of advanced teaching material for specialized seminars, courses and schools Both monographs and multi-author volumes will be considered for publication. Edited volumes should, however, consist of a very limited number of contributions only. -

0 2 0 Material Safety Data Sheet
He a lt h 2 0 Fire 0 2 0 Re a c t iv it y 0 Pe rs o n a l Pro t e c t io n E Material Safety Data Sheet Potassium nitrate MSDS Section 1: Chemical Product and Company Identification Product Name: Potassium nitrate Contact Information: Catalog Codes: SLP4009, SLP3001, SLP4816, SLP1987 Sciencelab.com, Inc. 14025 Smith Rd. CAS#: 7757-79-1 Houston, Texas 77396 RTECS: TT370000 US Sales: 1-800-901-7247 International Sales: 1-281-441-4400 TSCA: TSCA 8(b) inventory: Potassium nitrate Order Online: ScienceLab.com CI#: Not available. CHEMTREC (24HR Emergency Telephone), call: Synonym: Nitric Acid, potassium salt; saltpeter 1-800-424-9300 Chemical Name: Potassium Nitrate International CHEMTREC, call: 1-703-527-3887 Chemical Formula: KNO3 For non-emergency assistance, call: 1-281-441-4400 Section 2: Composition and Information on Ingredients Composition: Name CAS # % by Weight Potassium nitrate 7757-79-1 100 Toxicological Data on Ingredients: Potassium nitrate: ORAL (LD50): Acute: 3750 mg/kg [Rat]. 1901 mg/kg [Rabbit]. Section 3: Hazards Identification Potential Acute Health Effects: Hazardous in case of skin contact (irritant), of eye contact (irritant), of ingestion, of inhalation (lung irritant). Prolonged exposure may result in skin burns and ulcerations. Over-exposure by inhalation may cause respiratory irritation. Potential Chronic Health Effects: CARCINOGENIC EFFECTS: Not available. MUTAGENIC EFFECTS: Not available. TERATOGENIC EFFECTS: Not available. DEVELOPMENTAL TOXICITY: Not available. The substance may be toxic to blood, kidneys, central nervous system (CNS). Repeated or prolonged exposure to the substance can produce target organs damage. Section 4: First Aid Measures Eye Contact: Check for and remove any contact lenses. -

Jeffrey E. Lucius U.S. Geological Survey This Report Is Preliminary
U. S. DEPARTMENT OF THE INTERIOR GEOLOGICAL SURVEY PHYSICAL AND CHEMICAL PROPERTIES AND HEALTH EFFECTS OF THIRTY-THREE TOXIC ORGANIC CHEMICALS Jeffrey E. Lucius U.S. Geological Survey Open-File Report 87-428 August 1987 This report is preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards. Any use of trade names is for descriptive purposes only and does not imply endorsement by the U.S. Geological Survey. CONTENTS Page Introduction 4 The Properties 6 Abbreviations 13 Conversion Factors 16 Summary Tables 17 Acetic acid 27 Acetone 31 Benzene 34 Bis(2-ethylhexyl)phthalate 37 Bromoform 39 Carbon tetrachloride 42 Chlorobenzene 46 Chloroethane 49 Chloroform 52 Cyclohexane 55 Di-n-butyl phthalate 58 1.1-Dichloroethane 60 1.2-Dichloroethane 63 1,1-Dichloroethene 66 trans-1,2-Dichloroethene 69 Dimethyl sulfoxide 71 1,4-Dioxane 74 Ethanol 77 Ethylbenzene 81 Ethylene dibromide 84 Methanol 87 Methylene chloride 91 Naphthalene 94 Phenol 97 Quinoline 101 Tetrachloroethene 103 Toluene 106 1,1,1-Trichloroethane 109 Trichloroethene 112 Vinyl chloride 115 Water 118 m-Xylene 121 o-Xylene 124 p-Xylene 127 References and Bibliography 130 SUMMARY TABLES page 1. Ranking of top 20 organic ground water contaminants based on number of sites at which each contaminant was detected. 17 2. Selected toxic organic chemicals ordered by Chemical Abstract Service Registry Number (CAS RN). Those chemicals on the U.S. EPA top 100 hazardous substances list are also noted. 18 3. Selected toxic organic chemicals ordered by number of carbon and hydrogen atoms. 19 4. Ranking of selected toxic organic chemicals by specific gravity at room temperature. -

421 Liquid Tin Mektronics Version No: 6.11 Issue Date: 03/01/2019 Safety Data Sheet According to WHS and ADG Requirements Print Date: 03/01/2019 L.GHS.AUS.EN
421 Liquid Tin Mektronics Version No: 6.11 Issue Date: 03/01/2019 Safety Data Sheet according to WHS and ADG requirements Print Date: 03/01/2019 L.GHS.AUS.EN SECTION 1 IDENTIFICATION OF THE SUBSTANCE / MIXTURE AND OF THE COMPANY / UNDERTAKING Product Identifier Product name 421 Synonyms SDS Code: 421-liquid, 421-125ML, 421-500ML Other means of identification Liquid Tin Relevant identified uses of the substance or mixture and uses advised against Relevant identified uses Tin plates copper circuits Details of the supplier of the safety data sheet Registered company name Mektronics MG Chemicals (Head office) Address Unit 3 8 Bonz Place, Seven Hills NSW 2147 Australia 9347 - 193 Street Surrey V4N 4E7 British Columbia Canada Telephone 1300 788 701 +(1) 800-201-8822 Fax 1300 722 004 +(1) 800-708-9888 Website www.mektronics.com.au www.mgchemicals.com Email [email protected] [email protected] Emergency telephone number Association / Organisation CHEMTREC Australia Not Available Emergency telephone numbers +(61) 2-9037-2994 Not Available Other emergency telephone +(1) 703-527-3887 Not Available numbers SECTION 2 HAZARDS IDENTIFICATION Classification of the substance or mixture Poisons Schedule Not Applicable Acute Toxicity (Oral) Category 4, Skin Corrosion/Irritation Category 1C, Skin Sensitizer Category 1B, Carcinogenicity Category 2, Reproductive Toxicity Classification [1] Category 2, Chronic Aquatic Hazard Category 3 Legend: 1. Classified by Chemwatch; 2. Classification drawn from HSIS; 3. Classification drawn from Regulation (EU) No 1272/2008 - Annex VI Label elements Hazard pictogram(s) SIGNAL WORD DANGER Hazard statement(s) H302 Harmful if swallowed. H314 Causes severe skin burns and eye damage. -

Silicene, Siloxene, Or Silicane? Revealing the Structure and Optical Properties of Silicon Nanosheets Derived from Calcium Disilicide
Chemistry Publications Chemistry 1-28-2020 Silicene, Siloxene, or Silicane? Revealing the Structure and Optical Properties of Silicon Nanosheets Derived from Calcium Disilicide Bradley J. Ryan Iowa State University, [email protected] Michael P. Hanrahan Iowa State University and Ames Laboratory, [email protected] Yujie Wang Iowa State University Utkarsh Ramesh Iowa State University, [email protected] Charles K. A. Nyamekye Iowa State University and Ames Laboratory, [email protected] See next page for additional authors Follow this and additional works at: https://lib.dr.iastate.edu/chem_pubs Part of the Materials Chemistry Commons The complete bibliographic information for this item can be found at https://lib.dr.iastate.edu/ chem_pubs/1184. For information on how to cite this item, please visit http://lib.dr.iastate.edu/ howtocite.html. This Article is brought to you for free and open access by the Chemistry at Iowa State University Digital Repository. It has been accepted for inclusion in Chemistry Publications by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Silicene, Siloxene, or Silicane? Revealing the Structure and Optical Properties of Silicon Nanosheets Derived from Calcium Disilicide Abstract Si-nanosheets (Si-NSs) have recently attracted considerable attention due to their potential as next- generation materials for electronic, optoelectronic, spintronic, and catalytic applications. Even though monolayer Si-NSs were first synthesized over 150 years ago via topotactic deintercalation of CaSi2, there is a lack of consensus within the literature regarding the structure and optical properties of this material. Herein, we provide conclusive evidence of the structural and chemical properties of Si-NSs produced by the deintercalation of CaSi2 with cold (~ –30 °C) aqueous HCl, and characterize their optical properties. -

Electronic and Structural Properties of Superconducting Diborides And
Electronic and structural properties of superconducting diborides and calcium disilicide in the AlB2 structure G. Satta†, G. Profeta∗, F. Bernardini†, A. Continenza∗ and S. Massidda† ∗Istituto Nazionale di Fisica della Materia (INFM) and Dipartimento di Fisica, Universit`adegli Studi di L’Aquila, I–67010 Coppito (L’Aquila), Italy †Istituto Nazionale di Fisica della Materia (INFM) and Dipartimento di Fisica Universit`adegli Studi di Cagliari, 09124 Cagliari, Italy Abstract We report a detailed study of the electronic and structural properties of the 39K superconductor MgB2 and of several related systems of the same fam- ily, namely Mg0.5Al0.5B2, BeB2, CaSi2 and CaBe0.5Si1.5. Our calculations, which include zone-center phonon frequencies and transport properties, are performed within the local density approximation to the density functional theory, using the full-potential linearized augmented plane wave (FLAPW) and the norm-conserving pseudopotential methods. Our results indicate es- sentially three-dimensional properties for these compounds; however, strongly two-dimensional σ-bonding bands contribute significantly at the Fermi level. Similarities and differences between MgB2 and BeB2 (whose superconduct- ing properties have not been yet investigated) are analyzed in detail. Our calculations for Mg0.5Al0.5B2 show that metal substitution cannot be fully described in a rigid band model. CaSi2 is studied as a function of pressure, and Be substitution in the Si planes leads to a stable compound similar in many aspects to diborides. PACS numbers: 74.25.jb, 74.70.-b, 74.10.+v, 71.20.-b arXiv:cond-mat/0102358v2 [cond-mat.supr-con] 21 Feb 2001 Typeset using REVTEX 1 I. -

0332 Date: January 2004 Revision: August 2009 DOT Number: UN 1405
Right to Know Hazardous Substance Fact Sheet Common Name: CALCIUM SILICIDE Synonyms: Calcium Disilicide; Calcium Silicon CAS Number: 12013-56-8 Chemical Name: Calcium Silicide RTK Substance Number: 0332 Date: January 2004 Revision: August 2009 DOT Number: UN 1405 Description and Use EMERGENCY RESPONDERS >>>> SEE LAST PAGE Calcium Silicide is a gray, to black or brown, powder or chip Hazard Summary with a repulsive odor. It is used for making special metal Hazard Rating NJDOH NFPA alloys, in pyrotechnics, and as a deoxidizer. HEALTH 1 - FLAMMABILITY 3 - REACTIVITY 2 W - FLAMMABLE AND WATER REACTIVE POISONOUS GASES ARE PRODUCED IN FIRE CONTAINERS MAY EXPLODE IN FIRE Reasons for Citation Hazard Rating Key: 0=minimal; 1=slight; 2=moderate; 3=serious; f Calcium Silicide is on the Right to Know Hazardous 4=severe Substance List because it is cited by DOT. f This chemical is on the Special Health Hazard Substance f Calcium Silicide can affect you when inhaled. List. f Contact can irritate the skin and eyes. f Inhaling Calcium Silicide can irritate the nose, throat and lungs. f Calcium Silicide is FLAMMABLE and REACTIVE and a DANGEROUS FIRE and EXPLOSION HAZARD. SEE GLOSSARY ON PAGE 5. Workplace Exposure Limits FIRST AID No occupational exposure limits have been established for Eye Contact Calcium Silicide. However, it may pose a health risk. Always f Immediately flush with large amounts of water for at least 15 follow safe work practices. minutes, lifting upper and lower lids. Remove contact lenses, if worn, while rinsing. Skin Contact f Remove contaminated clothing and wash contaminated skin with soap and water. -
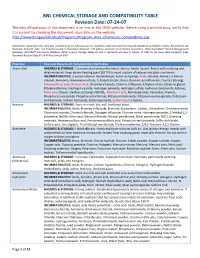
BNL CHEMICAL STORAGE and COMPATIBILITY TABLE Revision Date: 07-24-07 the Only Official Copy of This Document Is On-Line at the SHSD Website
BNL CHEMICAL STORAGE AND COMPATIBILITY TABLE Revision Date: 07-24-07 The only official copy of this document is on-line at the SHSD website. Before using a printed copy, verify that it is current by checking the document issue date on the website. http://www.bnl.gov/esh/shsd/Programs/Program_Area_Chemicals_Compatibility.asp Information contained in this table was compiled from the following sources: Academic Laboratory Chemical Hazards Guidebook by William J. Mahn, Published by Van Nostrand, Reinhold, 1991; Fire Protection Guide to Hazardous Materials 11th edition, National Fire Protection Association, 1994; Hazardtext® Hazard Managements Database; INFOTEXT® Documents Database; Better Science Through Safety by Jack A. Gerlovich and Gary E. Downs, © 1981 by the Iowa State University Press. Document Revision Date 07-24-07 Ken Erickson CHO Chemical Chemical Hazard and Compatibility Information Acetic Acid HAZARDS & STORAGE: Corrosive and combustible liquid. Serious health hazard. Reacts with oxidizing and alkali materials. Keep above freezing point (62 ºF) to avoid rupture of carboys and glass containers. INCOMPATIBILITIES: 2-amino-ethanol, Acetaldehyde, Acetic anhydride, Acids, Alcohol, Amines, 2-Amino- ethanol, Ammonia, Ammonium nitrate, 5-Azidotetrazole, Bases, Bromine pentafluoride, Caustics (strong), Chlorosulfonic acid, Chromic Acid, Chromium trioxide, Chlorine trifluoride, Ethylene imine, Ethylene glycol, Ethylene diamine, Hydrogen cyanide, Hydrogen peroxide, Hydrogen sulfide, Hydroxyl compounds, Ketones, Nitric Acid, Oleum, Oxidizers -

Publikationen Prof. Gotthard Seifert – 1976 Bis 2016
Publikationen Prof. Gotthard Seifert – 1976 bis 2016 Stand 20.10.2016 1. Raychev, D.; Guskova, O.; Seifert, G.; Sommer, J.-U., Conformational and electronic properties of small benzothiadiazole-cored oligomers with aryl flanking units: Thiophene versus Furan. Computational Materials Science 2016, 126, 287–298. 2. Sandonas, L. M.; Teich, D.; Gutierrez, R.; Lorenz, T.; Pecchia, A.; Seifert, G.; Cuniberti, G., Anisotropic Thermoelectric Response in Two-Dimensional Puckered Structures. Journal of Physical Chemistry C 2016, 120, (33), 18841–49. 3. Karpov, Y.; Erdmann, T.; Raguzin, I.; Al-Hussein, M.; Binner, M.; Lappan, U.; Stamm, M.; Gerasimov, K. L.; Beryozkina, T.; Bakulev, V.; Anokhin, D. V.; Ivanov, D. A.; Günther, F.; Gemming, S.; Seifert, G.; Voit, B.; Pietro, R. D.; Kiriy, A., High Conductivity in Molecularly p-Doped Diketopyrrolopyrrole-Based Polymer: The Impact of a High Dopant Strength and Good Structural Order. Advanced Materials 2016, 28, 6003-10. 4. Tranca, D. C.; Seifert, G., A First-Principles Study of Metal-Decorated Graphene Nanoribbons for Hydrogen Storage. Zeitschrift für Physikalische Chemie 2016, 230, (1), 791–808. 5. Schwalbe, S.; Trepte, K.; Seifert, G.; Kortus, J., Screening for high-spin metal organic frameworks (MOFs): density functional theory study on DUT-8(M-1,M-2) (with M-i = V, ... ,Cu). Physical Chemistry Chemical Physics 2016, 18, (11), 8075-8080. 6. Rodríguez-Hernández, F.; Tranca, D. C.; Szyja, B. M.; Santen, R. A. v.; Martínez-Mesa, A.; Uranga- Piña, L.; Seifert, G., Water Splitting on TiO2-Based Electrochemical Cells: A Small Cluster Study. Journal of Physical Chemistry C 2016, 120, 437–449. 7. Radovsky, G.; Popovitz-Biro, R.; Lorenz, T.; Joswig, J.-O.; Seifert, G.; Houben, L.; Dunin-Borkowski, R. -

Two-Dimensional Building Blocks for the Synthesis of Layered Hybrid
Dissertation zur Erlangung des Doktorgrades der Fakultät für Chemie und Pharmazie der Ludwig-Maximilians-Universität München TWO-DIMENSIONAL BUILDING BLOCKS FOR THE SYNTHESIS OF LAYERED HYBRID MATERIALS Stephan Werner aus Wiesbaden, Deutschland 2014 Erklärung Diese Dissertation wurde im Sinne von § 7 der Promotionsordnung vom 28. November 2011 von Frau Prof. Dr. Bettina V. Lotsch betreut. Eidesstattliche Versicherung Diese Dissertation wurde eigenständig und ohne unerlaubte Hilfe erarbeitet. München, 23.06.2014 …………………………………… (Stephan Werner) Dissertation eingereicht am 23.06.2014 1. Gutachter: Prof. Dr. Bettina V. Lotsch 2. Gutachter: Prof. Dr. Christina Scheu Mündliche Prüfung am 14.07.2014 Für Mama und Papa ACKNOWLEDGEMENTS First, I would like to express my gratitude to my supervisor Prof. Dr. Bettina V. Lotsch for giving me the opportunity to do research in her group. Throughout the entire time of work, I appreciated her expertise, the many helpful discussions and help at all times as well as the academic freedom in research. For being the co-referee of my thesis, for many helpful discussions and for help in TEM questions, I thank Prof. Dr. Christina Scheu. I want to thank Prof. Dr. Hans-Christian Böttcher, Prof. Dr. Konstantin Karaghiosoff, Prof. Dr. Dina Fattakhova-Rohlfing and Prof. Dr. Achim Hartschuh for being available as co- examiners in my viva voce. Furthermore, I would like to thank the following colleagues: . Prof. Hauke Clausen-Schaumann for his help and introduction into AFM theory and practice. Vincent Lau for electrochemical measurements and helpful discussions. Viola Duppel, Christian Ziegler and Kulpreet Virdi for TEM measurements and many helpful discussions upon interpretation of the results. -

GHS Safety Data Sheet SDS No
CaSi2 ; CAI04PAEG ; 2019/04/03 1 / 4 GHS Safety Data Sheet SDS No. : CAI04PAEG Date Issued : 2019/04/03 Section 1. Identification of the substance or mixture and of the supplier Product Information Product name: CaSi2 Calcium silicide Product number: Purity Form Size or Shape CAI06PB 99%(2N) powder - Company Information: Manufacturer : Kojundo Chemical Laboratory Co., Ltd. 1-28, 5-chome, Chiyoda, Sakado-shi, Saitama Japan 350-0284 Phone: +81-49-284-1511 Fax: +81-49-284-1351 Emergency Phone : +81-49-284-1511 Recommended uses and restrictions on use: For research purposes Section 2. Hazards identification GHS Classification Health Hazards Environmental Hazards Physical Hazards Substances and mixtures which, No data available No data available in contact with water, emit flammable gases : Category 2 GHS Label: F Pictograms or symbols: Warning word: WARNING Hazard information Description of precaution In conotact with water releases Keep away from any possible contact with water, because of violent reaction and flammable gas possible flash fire. Protect from moisture. Handle under inert gas. IN CASE OF FIRE: Wear protective gloves/eye protection/face protection. Use 《refer to our SDS》 to extinguish. IF ON SKIN: Wash skin with plenty of soap and water. If skin irritation occurs, get medical advice/attention. Protect from sunlight. Store in a cool, dry and well-ventilated place. Keep container tightly closed. Dispose of contents/ container in accordance with local/national regulations. Section 3. Composition / information on ingredients Chemical or common name: Calcium silicide Synonyms: Calcium disilicide Chemical formula: CaSi2 Single Substance or Compound: Single substance Composition: 100% CAS #: 12013-56-8 RTECS#: not listed TSCA inventory : listed EINECS: 2345887 CaSi2 ; CAI04PAEG ; 2019/04/03 2 / 4 Section 4. -
Properties and Hazards of 108 Selected Substances -1992 Edition
U. S. DEPARTMENT OF THE INTERIOR GEOLOGICAL SURVEY PROPERTIES AND HAZARDS OF 108 SELECTED SUBSTANCES -1992 EDITION Jeffrey E. Lucius1, Gary R. Olhoeft1, Patricia L. Hill1, and Steven K. Duke2 U.S. Geological Survey Open-File Report 92-527 September 1992 This report is preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. 1 Golden, CO, USA 2 now with Woodward-Clyde Consultants, 2020 E. First Street, Suite 900, Santa Ana, CA 92705 iii CONTENTS List of Tables ....................................................... vi Notice ............................................................... vii Introduction ......................................................... 1 Properties Definitions ................................................... 4 Key to Abbreviations .......................................... 13 Conversion Factors ............................................ 16 Tables .............................................................. 18 Substances .............................. GAS RN Acetic acid .................... 64-19-7 .................. 70 Acetone ........................ 67-64-1 .................. 75 Acrolein ....................... 107-02-8 .................. 81 Acrylonitrile .................. 107-13-1 .................. 85 Aldrin ......................... 309-00-2 .................. 89 Ammonia ........................ 7664-41-7 .................. 92