Planar and Sphericaltrigonometry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission. -

Can One Design a Geometry Engine? on the (Un) Decidability of Affine
Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A. -
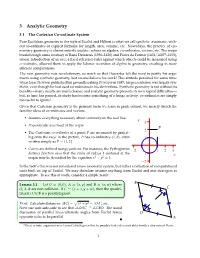
3 Analytic Geometry
3 Analytic Geometry 3.1 The Cartesian Co-ordinate System Pure Euclidean geometry in the style of Euclid and Hilbert is what we call synthetic: axiomatic, with- out co-ordinates or explicit formulæ for length, area, volume, etc. Nowadays, the practice of ele- mentary geometry is almost entirely analytic: reliant on algebra, co-ordinates, vectors, etc. The major breakthrough came courtesy of Rene´ Descartes (1596–1650) and Pierre de Fermat (1601/16071–1655), whose introduction of an axis, a fixed reference ruler against which objects could be measured using co-ordinates, allowed them to apply the Islamic invention of algebra to geometry, resulting in more efficient computations. The new geometry was revolutionary, so much so that Descartes felt the need to justify his argu- ments using synthetic geometry, lest no-one believe his work! This attitude persisted for some time: when Issac Newton published his groundbreaking Principia in 1687, his presentation was largely syn- thetic, even though he had used co-ordinates in his derivations. Synthetic geometry is not without its benefits—many results are much cleaner, and analytic geometry presents its own logical difficulties— but, as time has passed, its study has become something of a fringe activity: co-ordinates are simply too useful to ignore! Given that Cartesian geometry is the primary form we learn in grade-school, we merely sketch the familiar ideas of co-ordinates and vectors. • Assume everything necessary about on the real line. continuity y 3 • Perpendicular axes meet at the origin. P 2 • The Cartesian co-ordinates of a point P are measured by project- ing onto the axes: in the picture, P has co-ordinates (1, 2), often 1 written simply as P = (1, 2). -

Synthetic and Analytic Geometry
CHAPTER I SYNTHETIC AND ANALYTIC GEOMETRY The purpose of this chapter is to review some basic facts from classical deductive geometry and coordinate geometry from slightly more advanced viewpoints. The latter reflect the approaches taken in subsequent chapters of these notes. 1. Axioms for Euclidean geometry During the 19th century, mathematicians recognized that the logical foundations of their subject had to be re-examined and strengthened. In particular, it was very apparent that the axiomatic setting for geometry in Euclid's Elements requires nontrivial modifications. Several ways of doing this were worked out by the end of the century, and in 1900 D. Hilbert1 (1862{1943) gave a definitive account of the modern foundations in his highly influential book, Foundations of Geometry. Mathematical theories begin with primitive concepts, which are not formally defined, and as- sumptions or axioms which describe the basic relations among the concepts. In Hilbert's setting there are six primitive concepts: Points, lines, the notion of one point lying between two others (betweenness), congruence of segments (same distances between the endpoints) and congruence of angles (same angular measurement in degrees or radians). The axioms on these undefined concepts are divided into five classes: Incidence, order, congruence, parallelism and continuity. One notable feature of this classification is that only one class (congruence) requires the use of all six primitive concepts. More precisely, the concepts needed for the axiom classes are given as follows: Axiom class Concepts required Incidence Point, line, plane Order Point, line, plane, betweenness Congruence All six Parallelism Point, line, plane Continuity Point, line, plane, betweenness Strictly speaking, Hilbert's treatment of continuity involves congruence of segments, but the continuity axiom may be formulated without this concept (see Forder, Foundations of Euclidean Geometry, p. -

Is Geometry Analytic? Mghanga David Mwakima
IS GEOMETRY ANALYTIC? MGHANGA DAVID MWAKIMA 1. INTRODUCTION In the fourth chapter of Language, Truth and Logic, Ayer undertakes the task of showing how a priori knowledge of mathematics and logic is possible. In doing so, he argues that only if we understand mathematics and logic as analytic,1 by which he memorably meant “devoid of factual content”2, do we have a justified account of 3 a priori knowledgeδιανοια of these disciplines. In this chapter, it is not clear whether Ayer gives an argument per se for the analyticity of mathematics and logic. For when one reads that chapter, one sees that Ayer is mainly criticizing the views held by Kant and Mill with respect to arithmetic.4 Nevertheless, I believe that the positive argument is present. Ayer’s discussion of geometry5 in this chapter shows that it is this discussion which constitutes his positive argument for the thesis that analytic sentences are true 1 Now, I am aware that ‘analytic’ was understood differently by Kant, Carnap, Ayer, Quine, and Putnam. It is not even clear whether there is even an agreed definition of ‘analytic’ today. For the purposes of my paper, the meaning of ‘analytic’ is Carnap’s sense as described in: Michael, Friedman, Reconsidering Logical Positivism (New York: Cambridge University Press, 1999), in terms of the relativized a priori. 2 Alfred Jules, Ayer, Language, Truth and Logic (New York: Dover Publications, 1952), p. 79, 87. In these sections of the book, I think the reason Ayer chose to characterize analytic statements as “devoid of factual” content is in order to give an account of why analytic statements could not be shown to be false on the basis of observation. -

A Diagrammatic Formal System for Euclidean Geometry
A DIAGRAMMATIC FORMAL SYSTEM FOR EUCLIDEAN GEOMETRY A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy by Nathaniel Gregory Miller May 2001 c 2001 Nathaniel Gregory Miller ALL RIGHTS RESERVED A DIAGRAMMATIC FORMAL SYSTEM FOR EUCLIDEAN GEOMETRY Nathaniel Gregory Miller, Ph.D. Cornell University 2001 It has long been commonly assumed that geometric diagrams can only be used as aids to human intuition and cannot be used in rigorous proofs of theorems of Euclidean geometry. This work gives a formal system FG whose basic syntactic objects are geometric diagrams and which is strong enough to formalize most if not all of what is contained in the first several books of Euclid’s Elements.Thisformal system is much more natural than other formalizations of geometry have been. Most correct informal geometric proofs using diagrams can be translated fairly easily into this system, and formal proofs in this system are not significantly harder to understand than the corresponding informal proofs. It has also been adapted into a computer system called CDEG (Computerized Diagrammatic Euclidean Geometry) for giving formal geometric proofs using diagrams. The formal system FG is used here to prove meta-mathematical and complexity theoretic results about the logical structure of Euclidean geometry and the uses of diagrams in geometry. Biographical Sketch Nathaniel Miller was born on September 5, 1972 in Berkeley, California, and grew up in Guilford, CT, Evanston, IL, and Newtown, CT. After graduating from Newtown High School in 1990, he attended Princeton University and graduated cum laude in mathematics in 1994. -

Apollonius Problem
Journal of Computer-Generated Euclidean Geometry Apollonius Problem Deko Dekov Abstract. Given three non-intersecting circles, there are eight circles that are tangent to each of the given circles. We note that these eight circles form four pairs of circles such that the circles of a pair are inverses in the radical circle of the given three circles. The famous Apollonius problem includes the following problem: Given three non- intersecting circles, to construct all circles that are tangent to each of the given circles. There are eight total solutions. Construction of these eight circles, using the method due to Joseph Gergonne (1771-1859), is given, e.g. in Geometric Constructions [5]. Denote by 1 and 2 the Apollonius circles tangent respective externally and internally to the three given circles. If the given three circles are the three excircles of a given triangle, then circle 1 is the nine- point circle and circle 2 is the Apollonius circle of the given triangle. Paul Yiu [9] (see also Grinberg and Yiu [3]) noticed that the Apollonius circle of the given triangle is inverse image of the nine-point circle in the radical circle of the excircles. If the given three circles are the three Lucas circles of a given triangle, then circle 1 is the inner Soddy circle of the Lucas circles and circle 2 is the outer Soddy circle of the Lucas circles. In this case circle 2 coincides with the circumcircle of the given triangle. Peter Moses [6] noticed that the inner Soddy circle of the Lucas circles is the inverse image of the circumcircle of the given triangle. -

The Pythagorean Theorem: What Is It About?
THE PYTHAGOREAN THEOREM: WHAT IS IT ABOUT? ALEXANDER GIVENTAL Although twenty five centuries old, the Pythagorean theorem appears vigor- ous and ubiquitous. A key to the distance formula in Descartes’s method of coordinates, the theorem is implicitly present in all scientific models and engineering computations involving spatial relationships or trigonometry. An invisible companion to the dot-product operation, it is inherent in equations of mathematical physics and continuum mechanics, be those Laplace, Navier- Stokes, Maxwell or Yang-Mills. Disguised by axiomatic constructions of linear algebra and Riemannian geometry, it animates both quantum physics and Ein- stein’s gravitation, which are otherwise so hard to reconcile. And of course, a rare day of a statistician or experimenter goes by without Euclid’s nightmare— fitting any three or more points into a straight line, which is accomplished by Gaussian least squares and hence is also reminiscent of Pythagoras. Quite deservedly, therefore, the philosopher’s pants are proudly displayed in middle-school textbooks to represent, perhaps, the only scientific truth circu- lating among the general public “with proof.” The most popular one (shown in Figure 1) is very convincing indeed. Yet it pictures the whole issue as a cut-and-paste puzzle and leaves us with a feeling of disproportion: one of the most fundamental facts of nature is due to an ingenious tiling trick. The vast majority of other proofs 1 are similar in nature. B C A Figure 1. A + B = C. 1 Of dozens, if not hundreds (see http://www.cut-the-knot.org/pythagoras/index.shtml and references therein). -

Euclidean Geometry
Euclidean Geometry Rich Cochrane Andrew McGettigan Fine Art Maths Centre Central Saint Martins http://maths.myblog.arts.ac.uk/ Reviewer: Prof Jeremy Gray, Open University October 2015 www.mathcentre.co.uk This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. 2 Contents Introduction 5 What's in this Booklet? 5 To the Student 6 To the Teacher 7 Toolkit 7 On Geogebra 8 Acknowledgements 10 Background Material 11 The Importance of Method 12 First Session: Tools, Methods, Attitudes & Goals 15 What is a Construction? 15 A Note on Lines 16 Copy a Line segment & Draw a Circle 17 Equilateral Triangle 23 Perpendicular Bisector 24 Angle Bisector 25 Angle Made by Lines 26 The Regular Hexagon 27 © Rich Cochrane & Andrew McGettigan Reviewer: Jeremy Gray www.mathcentre.co.uk Central Saint Martins, UAL Open University 3 Second Session: Parallel and Perpendicular 30 Addition & Subtraction of Lengths 30 Addition & Subtraction of Angles 33 Perpendicular Lines 35 Parallel Lines 39 Parallel Lines & Angles 42 Constructing Parallel Lines 44 Squares & Other Parallelograms 44 Division of a Line Segment into Several Parts 50 Thales' Theorem 52 Third Session: Making Sense of Area 53 Congruence, Measurement & Area 53 Zero, One & Two Dimensions 54 Congruent Triangles 54 Triangles & Parallelograms 56 Quadrature 58 Pythagoras' Theorem 58 A Quadrature Construction 64 Summing the Areas of Squares 67 Fourth Session: Tilings 69 The Idea of a Tiling 69 Euclidean & Related Tilings 69 Islamic Tilings 73 Further Tilings -

Chapter 4 Euclidean Geometry
Chapter 4 Euclidean Geometry Based on previous 15 axioms, The parallel postulate for Euclidean geometry is added in this chapter. 4.1 Euclidean Parallelism, Existence of Rectangles De¯nition 4.1 Two distinct lines ` and m are said to be parallel ( and we write `km) i® they lie in the same plane and do not meet. Terminologies: 1. Transversal: a line intersecting two other lines. 2. Alternate interior angles 3. Corresponding angles 4. Interior angles on the same side of transversal 56 Yi Wang Chapter 4. Euclidean Geometry 57 Theorem 4.2 (Parallelism in absolute geometry) If two lines in the same plane are cut by a transversal to that a pair of alternate interior angles are congruent, the lines are parallel. Remark: Although this theorem involves parallel lines, it does not use the parallel postulate and is valid in absolute geometry. Proof: Assume to the contrary that the two lines meet, then use Exterior Angle Inequality to draw a contradiction. 2 The converse of above theorem is the Euclidean Parallel Postulate. Euclid's Fifth Postulate of Parallels If two lines in the same plane are cut by a transversal so that the sum of the measures of a pair of interior angles on the same side of the transversal is less than 180, the lines will meet on that side of the transversal. In e®ect, this says If m\1 + m\2 6= 180; then ` is not parallel to m Yi Wang Chapter 4. Euclidean Geometry 58 It's contrapositive is If `km; then m\1 + m\2 = 180( or m\2 = m\3): Three possible notions of parallelism Consider in a single ¯xed plane a line ` and a point P not on it. -

Differential Geometry Curves – Surfaces – Manifolds Third Edition
STUDENT MATHEMATICAL LIBRARY Volume 77 Differential Geometry Curves – Surfaces – Manifolds Third Edition Wolfgang Kühnel Differential Geometry Curves–Surfaces– Manifolds http://dx.doi.org/10.1090/stml/077 STUDENT MATHEMATICAL LIBRARY Volume 77 Differential Geometry Curves–Surfaces– Manifolds Third Edition Wolfgang Kühnel Translated by Bruce Hunt American Mathematical Society Providence, Rhode Island Editorial Board Satyan L. Devadoss John Stillwell (Chair) Erica Flapan Serge Tabachnikov Translation from German language edition: Differentialgeometrie by Wolfgang K¨uhnel, c 2013 Springer Vieweg | Springer Fachmedien Wies- baden GmbH JAHR (formerly Vieweg+Teubner). Springer Fachmedien is part of Springer Science+Business Media. All rights reserved. Translated by Bruce Hunt, with corrections and additions by the author. Front and back cover image by Mario B. Schulz. 2010 Mathematics Subject Classification. Primary 53-01. For additional information and updates on this book, visit www.ams.org/bookpages/stml-77 Page 403 constitutes an extension of this copyright page. Library of Congress Cataloging-in-Publication Data K¨uhnel, Wolfgang, 1950– [Differentialgeometrie. English] Differential geometry : curves, surfaces, manifolds / Wolfgang K¨uhnel ; trans- lated by Bruce Hunt.— Third edition. pages cm. — (Student mathematical library ; volume 77) Includes bibliographical references and index. ISBN 978-1-4704-2320-9 (alk. paper) 1. Geometry, Differential. 2. Curves. 3. Surfaces. 4. Manifolds (Mathematics) I. Hunt, Bruce, 1958– II. Title. QA641.K9613 2015 516.36—dc23 2015018451 c 2015 by the American Mathematical Society. All rights reserved. The American Mathematical Society retains all rights except those granted to the United States Government. Printed in the United States of America. ∞ The paper used in this book is acid-free and falls within the guidelines established to ensure permanence and durability. -

THE PROBLEM of APOLLONIUS H. S. M. Coxeter 1. Introduction. On
THE PROBLEM OF APOLLONIUS H. S. M. Coxeter 1. Introduction. On behalf of the Canadian Mathematical Congress, I wish to thank the University of Toronto for its hospitality, the members of the Local Arrangements Committee (especially Chandler Davis) for the many comforts and pleasures they have provided, and our nine distinguished visitors for the courses of lectures they gave at our Seminar. Bearing in mind the subject of this afternoon's discussion, I -will try to show by some examples that good old-fashioned elementary geometry is not dead, that mathematics can be interesting without being obscure, and that clever ideas are not restricted to professionals. In the third century B.C., Apollonius of Perga wrote two books on Contacts (e IT afyai.), in which he proposed and solved his famous problem: given three things, each of which may be a point, a line, or a circle, construct a circle which passes through each of the points and touches the given lines and circles. The easy cases are covered in the first book, leaving most of the second for the really interesting case, when all the three "things" are circles. As Sir Thomas Heath remarks [10, p. 182], this problem "has exercised the ingenuity of many- distinguished geometers, including Vieta and Newton". I will not ask you to look at any of their methods for solving it. These are adequately treated in the standard textbooks [e. g. 11, p. 118]. Nor will I inflict on you an enumeration of the possible relations of incidence of the three given circles. This was done with great skill in 1896 by Muirhead [12].