Representativity of 2D Shape Parameters for Mineral Particles in Quantitative Petrography
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Sand-Gravel Marine Deposits and Grain-Size Properties
GRAVEL ISSN 1678-5975 Novembro - 2005 Nº 3 59-70 Porto Alegre Sand-Gravel Marine Deposits and Grain-Size Properties L. R. Martins1,2 & E. G. Barboza2 1 COMAR- South West Atlantic Coastal and Marine Geology Group; 2 Centro de Estudos de Geologia Costeira e Oceânica – CECO/IG/UFRGS. RESUMO A plataforma continental Atlântica do Rio Grande do Sul e Uruguai foi utilizada como laboratório natural para testar as relações entre propriedades de tamanho de grão e ambiente sedimentar. A evolução Pleistoceno/Holoceno da região foi intensamente estudada através de um mapeamento detalhado, e de estudos sedimentológicos e estratigráficos, oferecendo, dessa forma, uma excelente oportunidade para esse tipo de trabalho. Acumulações de areia e cascalho, vinculadas a níveis de estabilização identificados da transgressão Holocênica, localizados nas isóbatas de 110-120 e 20-30 metros, fornecem elementos confiáveis relacionados com a fonte, transporte e nível de energia de deposição e podem ser utilizados como linhas de evidencias na interpretação ambiental. ABSTRACT The Atlantic Rio Grande do Sul (Brazil) and Uruguay inner continental shelf was used as a natural laboratory to test the relationship between grain-size properties and sedimentary environment. The Pleistocene/Holocene evolution of the region was intensively studied through detailed mapping, sedimentological and stratigraphic research thus offering an excellent opportunity of developing this type of work. Sand and gravel deposits linked with identified stillstands of the Holocene transgression located at 110-120 and 20-30 meters isobath provided elements related to the source, transport and depositional energy level and can be used as a tool for environmental interpretation. Keywords: marine deposits, grain-size, sand-gravel, Holocene. -

Automatic Computation of Pebble Roundness Using Digital Imagery
Automatic computation of pebble roundness using digital imagery and discrete geometry Tristan Roussillon a, Herve´ Piegay´ b, Isabelle Sivignon c, Laure Tougne a, Franck Lavigne d aUniversity of Lyon, LIRIS, 5 Av Pierre-Mendes` France 69676 Bron bUniversity of Lyon, CNRS-UMR 5600 Environnement, Ville, Societ´ e,´ 15 Parvis Rene´ Descartes, 69364 Lyon cUniversity of Lyon, LIRIS, CNRS, 8 Bd Niels Bohr 69622 Villeurbanne dUniversity of Paris, CNRS-UMR 8591 Laboratoire de Geographie´ Physique, 1 place Aristide Briand, 92195 Meudon Abstract The shape of sedimentary particles is an important property, from which geographical hypotheses related to abrasion, distance of transport, river behavior, etc. can be formulated. In this paper, we use digital image analysis, especially discrete geometry, to automatically compute some shape parameters such as roundness i.e. a measure of how much the corners and edges of a particle have been worn away. In contrast to previous works in which traditional digital images analysis techniques such as Fourier transform (Diepenbroek et al., 1992, Sedimentology, 39) are used, we opted for a discrete geometry approach that allowed us to implement Wadell’s original index (Wadell, 1932, Journal of Geology, 40) which is known to be more accurate, but more time consuming to implement in the field (Pissart et al., 1998, G´eomorphologie: relief, processus, environnement, 3). Preprint submitted to Elsevier 23 October 2017 Our implementation of Wadell’s original index is highly correlated (92%) with the round- ness classes of Krumbein’s chart, used as a ground-truth (Krumbein, 1941, Journal of Sed- imentary Petrology, 11, 2). In addition, we show that other geometrical parameters, which are easier to compute, can be used to provide good approximations of roundness. -

Image Analysis: Evaluating Particle Shape
Image Analysis: Evaluating Particle Shape Jeffrey Bodycomb, Ph.D. HORIBA Scientific www.horiba.com/us/particle © 2011 HORIBA, Ltd. All rights reserved. Why Image Analysis? Verify/Supplement diffraction results (orthogonal technique) Replace sieves Need shape information, for example due to importance of powder flow These may have the same size (cross section), but behave very differently. © 2011 HORIBA, Ltd. All rights reserved. Why Image Analysis? Crystalline, acicular powders needs more than “equivalent diameter” We want to characterize a needle by the length (or better, length and width). © 2011 HORIBA, Ltd. All rights reserved. Why Image Analysis Pictures: contaminants, identification, degree of agglomeration Screen excipients, full morphology Root cause of error (tablet batches), combined w/other techniques Replace manual microscopy © 2011 HORIBA, Ltd. All rights reserved. Why Shape Information? Evaluating packing Evaluate flow of particles Evaluate flow around particles Retroreflection (optical properties) Properties of particles in aggregate (bulk) © 2011 HORIBA, Ltd. All rights reserved. Effect of Shape on Flow Yes, I assumed density doesn’t matter. Roundness is a measure based on particle perimeter. θc © 2011 HORIBA, Ltd. All rights reserved. Major Steps in Image Analysis Image Acquisition and enhancement Object/Phase detection Measurements © 2011 HORIBA, Ltd. All rights reserved. Two Approaches Dynamic: Static: particles flow past camera particles fixed on slide, stage moves slide 0.5 – 1000 microns 1 – 3000 microns 2000 microns w/1.25 objective © 2011 HORIBA, Ltd. All rights reserved. Size Parameters -> Shape Parameters Shape parameters are often calculated using size measures © 2011 HORIBA, Ltd. All rights reserved. Size Parameters Feret zMax (length) zPerpendicular to Max (width) zMin (width) zPerpendicular to Min (main length) Area zCircular Diameter zSpherical Diameter Perimeter Convex Perimeter © 2011 HORIBA, Ltd. -

Quick Guide to Precision Measuring Instruments
E4329 Quick Guide to Precision Measuring Instruments Coordinate Measuring Machines Vision Measuring Systems Form Measurement Optical Measuring Sensor Systems Test Equipment and Seismometers Digital Scale and DRO Systems Small Tool Instruments and Data Management Quick Guide to Precision Measuring Instruments Quick Guide to Precision Measuring Instruments 2 CONTENTS Meaning of Symbols 4 Conformance to CE Marking 5 Micrometers 6 Micrometer Heads 10 Internal Micrometers 14 Calipers 16 Height Gages 18 Dial Indicators/Dial Test Indicators 20 Gauge Blocks 24 Laser Scan Micrometers and Laser Indicators 26 Linear Gages 28 Linear Scales 30 Profile Projectors 32 Microscopes 34 Vision Measuring Machines 36 Surftest (Surface Roughness Testers) 38 Contracer (Contour Measuring Instruments) 40 Roundtest (Roundness Measuring Instruments) 42 Hardness Testing Machines 44 Vibration Measuring Instruments 46 Seismic Observation Equipment 48 Coordinate Measuring Machines 50 3 Quick Guide to Precision Measuring Instruments Quick Guide to Precision Measuring Instruments Meaning of Symbols ABSOLUTE Linear Encoder Mitutoyo's technology has realized the absolute position method (absolute method). With this method, you do not have to reset the system to zero after turning it off and then turning it on. The position information recorded on the scale is read every time. The following three types of absolute encoders are available: electrostatic capacitance model, electromagnetic induction model and model combining the electrostatic capacitance and optical methods. These encoders are widely used in a variety of measuring instruments as the length measuring system that can generate highly reliable measurement data. Advantages: 1. No count error occurs even if you move the slider or spindle extremely rapidly. 2. You do not have to reset the system to zero when turning on the system after turning it off*1. -

45. Sedimentary Facies and Depositional History of the Iberia Abyssal Plain1
Whitmarsh, R.B., Sawyer, D.S., Klaus, A., and Masson, D.G. (Eds.), 1996 Proceedings of the Ocean Drilling Program, Scientific Results, Vol. 149 45. SEDIMENTARY FACIES AND DEPOSITIONAL HISTORY OF THE IBERIA ABYSSAL PLAIN1 D. Milkert,2 B. Alonso,3 L. Liu,4 X. Zhao,5 M. Comas,6 and E. de Kaenel4 ABSTRACT During Leg 149, a transect of five sites (Sites 897 to 901) was cored across the rifted continental margin off the west coast of Portugal. Lithologic and seismostratigraphical studies, as well as paleomagnetic, calcareous nannofossil, foraminiferal, and dinocyst stratigraphic research, were completed. The depositional history of the Iberia Abyssal Plain is generally characterized by downslope transport of terrigenous sedi- ments, pelagic sedimentation, and contourite sediments. Sea-level changes and catastrophic events such as slope failure, trig- gered by earthquakes or oversteepening, are the main factors that have controlled the different sedimentary facies. We propose five stages for the evolution of the Iberia Abyssal Plain: (1) Upper Cretaceous and lower Tertiary gravitational flows, (2) Eocene pelagic sedimentation, (3) Oligocene and Miocene contourites, (4) a Miocene compressional phase, and (5) Pliocene and Pleistocene turbidite sedimentation. Major input of terrigenous turbidites on the Iberia Abyssal Plain began in the late Pliocene at 2.6 Ma. INTRODUCTION tured by both Mesozoic extension and Eocene compression (Pyrenean orogeny) (Boillot et al., 1979), and to a lesser extent by Miocene com- Leg 149 drilled a transect of sites (897 to 901) across the rifted mar- pression (Betic-Rif phase) (Mougenot et al., 1984). gin off Portugal over the ocean/continent transition in the Iberia Abys- Previous studies of the Cenozoic geology of the Iberian Margin sal Plain. -
New Parameter of Roundness R: Circularity Corrected by Aspect Ratio Yasuhiro Takashimizu1* and Maiko Iiyoshi2
Takashimizu and Iiyoshi Progress in Earth and Planetary Science (2016) 3:2 DOI 10.1186/s40645-015-0078-x METHODOLOGY Open Access New parameter of roundness R: circularity corrected by aspect ratio Yasuhiro Takashimizu1* and Maiko Iiyoshi2 Abstract In this paper, we propose a new roundness parameter R, to denote circularity corrected by aspect ratio. The basic concept of this new roundness parameter is given by the following equation: R = Circularity + (Circularity perfect circle Circularity aspect ratio) where Circularityperfect circle is the maximum value of circularity and Circularityaspect ratio is the circularity when only the aspect ratio varies from that of a perfect circle. Based on tests of digital circle and ellipse images using ImageJ software, the effective sizes and aspect ratios of such images for the calculation of R were found to range between 100 and 1024 pixels, and 10:1 to 10:10, respectively. R is thus given by R =CI + (0.913−CAR) where CI is the circularity measured using ImageJ software and CAR is the sixth-degree function of the aspect ratio measured using the same software. The correlation coefficient between the new parameter R and Krumbein’s roundness is 0.937 (adjusted coefficient of determination = 0.874). Results from the application of R to modern beach and slope deposits showed that R is able to quantitatively separate both types of material in terms of roundness. Therefore, we believe that the new roundness parameter R will be useful for performing precise statistical analyses of the roundness of particles in the future. Keywords: Aspect ratio, Circularity, ImageJ software, Krumbein’s visual roundness, Roundness Background not strictly quantitative. -

Orientation, Sphericity and Roundness Evaluation of Particles Using Alternative 3D Representations
Orientation, Sphericity and Roundness Evaluation of Particles Using Alternative 3D Representations Irving Cruz-Mat´ıasand Dolors Ayala Department de Llenguatges i Sistemes Inform´atics, Universitat Polit´ecnicade Catalunya, Barcelona, Spain December 2013 Abstract Sphericity and roundness indices have been used mainly in geology to analyze the shape of particles. In this paper, geometric methods are proposed as an alternative to evaluate the orientation, sphericity and roundness indices of 3D objects. In contrast to previous works based on digital images, which use the voxel model, we represent the particles with the Extreme Vertices Model, a very concise representation for binary volumes. We define the orientation with three mutually orthogonal unit vectors. Then, some sphericity indices based on length measurement of the three representative axes of the particle can be computed. In addition, we propose a ray-casting-like approach to evaluate a 3D roundness index. This method provides roundness measurements that are highly correlated with those provided by the Krumbein's chart and other previous approach. Finally, as an example we apply the presented methods to analyze the sphericity and roundness of a real silica nano dataset. Contents 1 Introduction 2 2 Related Work 4 2.1 Orientation . 4 2.2 Sphericity and Roundness . 4 3 Representation Model 7 3.1 Extreme Vertices Model . 7 4 Sphericity and Roundness Evaluation 9 4.1 Oriented Bounding Box Computation . 9 4.2 Sphericity Computation . 11 4.3 Roundness Computation . 12 5 EVM-roundness -

Particle Shape
PARTICLE SHAPE Prepared By : Bhavuk Sharma Course : M.Sc. Geology Assistant Professor Semester – IV Department of Geology , Course Code : MGELEC-1 Patna University , Patna Unit : Unit - III [email protected] CONTENTS 1. Introduction 2. Definitions 3. Measuring Particle Shape 4. Particle Form 5. Particle Roundness 6. Surface Texture 7. Exercise 8. References. INTRODUCTION The shape of sedimentary particles is an important physical attribute that may provide information about the sedimentary history of a deposit or the hydrodynamic behavior of particles in a transporting medium. It is determined by the following factors : Orientation and Original shapes of Spacing of mineral grain in fractures in the source rocks bedrock Nature and Sediment burial Intensity of processes sediment transport Particle shape, however, is a complex function of lithology, particle size, the mode and duration of transport, the energy of the transporting medium, the nature and extent of post-depositional weathering, and the history of sediment transport and deposition. DEFINITIONS Particle Shape is defined by three related but different aspects of grains : Form , Roundness and Surface Texture Measuring PARTICLE SHAPE • Standardized numerical shape indices have been developed to facilitate shape analyses by mathematical or graphical methods. • Quantitative measures of shape can be made on two-dimensional images or projections of particles or on the three-dimensional shape of individual particles. • Two-dimensional particle shape measurements are particularly applicable when individual particles cannot be extracted from the rock matrix. • Three-dimensional analyses of individual irregularly shaped particles generally involve measuring the principal axes of a triaxial ellipsoid to approximate particle shape. • The two-dimensional particle shape is generally considered to be a function of attrition and weathering during transport whereas three-dimensional shape is more closely related to particle lithology. -

Identifying Sediment Transport Mechanisms from Grain Size-Shape Distributions
https://doi.org/10.5194/esurf-2019-58 Preprint. Discussion started: 25 November 2019 c Author(s) 2019. CC BY 4.0 License. Identifying sediment transport mechanisms from grain size-shape distributions Johannes Albert van Hateren1, Unze van Buuren1, Sebastiaan Martinus Arens2, Ronald Theodorus van Balen1,3, Maarten Arnoud Prins1 5 1Faculty of Science, Department of Earth Sciences, Vrije Universiteit, Amsterdam, 1081 HV, The Netherlands 2Bureau for Beach and Dune Research, Soest, The Netherlands 3TNO-Geological Survey of the Netherlands, Utrecht, 3584 CB, The Netherlands Correspondence to: Hans van Hateren ([email protected]) 10 Abstract. The way in which sediment is transported (creep, saltation, suspension), is traditionally interpreted from grain size distribution characteristics. However, the grain size range associated with transitions from one transport mode to the other is highly variable because it depends on the amount of transport energy available. In this study we present a novel methodology for determination of the sediment transport mode based on grain size and shape data from dynamic image analysis. The data are integrated into grain size-shape distributions and primary components are determined using end-member modelling. In 15 real-world datasets, primary components can be interpreted in terms of different transport mechanisms and/or sediment sources. Accuracy of the method is assessed using artificial datasets with known primary components that are mixed in known proportions. The results show that the proposed technique accurately identifies primary components with the exception of those primary components that only form minor contributions to the samples (highly mixed components). 20 The new method is also tested on sediment samples from an active aeolian system in the Dutch coastal dunes. -

Bkecciation, Alteration, and Mineralization at The
Brecciation, alteration, and mineralization at the Copper Flat porphyry copper deposit, Hillsboro, New Mexico Item Type text; Thesis-Reproduction (electronic); maps Authors Fowler, Linda Leigh Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 02/10/2021 11:45:33 Link to Item http://hdl.handle.net/10150/557922 BKECCIATION, ALTERATION, AND MINERALIZATION AT THE COPPER FLAT PORPHYRY COPPER DEPOSIT, HILLSBORO, NEW MEXICO by Linda Leigh Fowler A Thesis Submitted to the Faculty of the DEPARTMENT OF GEOSCIENCES In Partial Fulfillment of the Requirements For the Degree of MASTER OF SCIENCE In the Graduate College THE UNIVERSITY OF ARIZONA 1 9 - 8 2 STATEMENT BY AUTHOR This thesis has been submitted in partial fulfillment of re quirements for an advanced degree at The University of Arizona and is deposited in the University Library to be made available to borrowers under rules of the Library. Brief quotations from this thesis are allowable without special permission, provided that accurate acknowledgment of source is made. Requests for permission for extended quotation from or reproduction of this manuscript in whole or in part may be granted by the head of the major department or the Dean of the Graduate College when in his judg ment the proposed use of the material is in the interests of scholar ship. In all other instances, however, permission must be obtained from the author. -
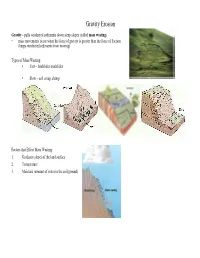
Gravity Erosion
Gravity Erosion Gravity - pulls weathered sediments down steep slopes (called mass wasting ) • mass movements occur when the force of gravity is greater than the force of friction (keeps weathered sediments from moving) Types of Mass Wasting: • Fast – landslides mudslides • Slow – soil creep, slump Factors that Effect Mass Wasting: 1. Gradient (slope) of the land surface 2. Temperature 3. Moisture (amount of water in the soil/ground) Wind Erosion Wind - heavy winds can move sand, but rarely more than a meter above the ground and only where it is very dry • light winds can only move the smallest sediments • occurs in arid climates and coastlines where where loose sediments are available Deflation - process where winds blow away loose sediments, lowering the land surface Abrasion - winds blow sand against rocks and other objects causing them to be "sandblasted" Arches Hoodoos Water Erosion Streams - running water is the dominant form of erosion • the amount (volume) of water in a stream is called the stream's discharge Factor's affecting a stream's discharge: 1. Season - discharge greatest in the spring 2. Climate - greatest in humid climates 3. Ground/Soil - greatest when soil is saturated 4. Weather - increases after a period of precipitation Streams carry sediments by: 1. Suspension - carried within the water column 2. Bouncing/Rolling - larger particles along the stream bottom 3. In-solution - minerals dissolved in the water • as sediments move in the water, the hit rocks, the stream channel, and other sediments - this causes the sediments to become rounded in a process called abrasion As the velocity of a stream increases, its kinetic energy increases and the amount of erosion it does will increase Factors that Affect Stream Velocity: 1. -

Modeling Three-Dimensional Shape of Sand Grains Using Discrete Element Method Nivedita Das University of South Florida
University of South Florida Scholar Commons Graduate Theses and Dissertations Graduate School 5-4-2007 Modeling Three-Dimensional Shape of Sand Grains Using Discrete Element Method Nivedita Das University of South Florida Follow this and additional works at: https://scholarcommons.usf.edu/etd Part of the American Studies Commons Scholar Commons Citation Das, Nivedita, "Modeling Three-Dimensional Shape of Sand Grains Using Discrete Element Method" (2007). Graduate Theses and Dissertations. https://scholarcommons.usf.edu/etd/689 This Dissertation is brought to you for free and open access by the Graduate School at Scholar Commons. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. Modeling Three-Dimensional Shape of Sand Grains Using Discrete Element Method by Nivedita Das A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy Department of Civil and Environmental Engineering College of Engineering University of South Florida Co-Major Professor: Alaa K. Ashmawy, Ph.D. Co-Major Professor: Sudeep Sarkar, Ph.D. Manjriker Gunaratne, Ph.D. Beena Sukumaran, Ph.D. Abla M. Zayed, Ph.D. Date of Approval: May 4, 2007 Keywords: Fourier transform, spherical harmonics, shape descriptors, skeletonization, angularity, roundness, liquefaction, overlapping discrete element cluster © Copyright 2007, Nivedita Das DEDICATION To my parents..... ACKNOWLEDGEMENTS First of all, I would like to thank my doctoral committee members – Dr. Alaa Ashmawy, Dr. Sudeep Sarkar, Dr. Manjriker Gunaratne, Dr. Abla Zayed and Dr. Beena Sukumaran for their insights and suggestions that have immensely contributed in improving the quality of this dissertation.