DOCSLIB.ORG

Methods for the Prediction of the Impact of Groundwater Abstraction on East Anglian Wetlands

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Methods for the Prediction of the Impact of Groundwater Abstraction on East Anglian Wetlands 5- ua.vo.oi r s r . Natural Environment Research Council British Geological Survey Institute of Hydrology Methods for the prediction of the impact of groundwater abstraction on East Anglian wetlands A Williams1, K Gilman2 & J Barker 1 BGS Hydrogeology Wallingford 2 IH Plynlimon This report is produced as part of NRA Project 01/558 'Protection of East Anglian wetlands' for NBA Anglian Region Bibliographic reference: Authors: A Williams, K Gilman &J Barker Title: Methods for the prediction of the impact of groundwater abstraction on East Anglian wetlands British Geological Survey report WD/95/SR © NERC 1995 Keyworth, Nottinghamshire British Geological Survey 1995 1 CONTENTS Executive summary Introduction 1 1.1 Background 1 1.2 Previous studies 2 1.3 Present study 3 Wetlands and water use 9 2.1 Wetland types 10 2.2 Water requirements of different plant types 11 2.3 The wetland water budget - sources of water 13 2.4 Estimation of present water balance and modelling the wetland water table 14 2.5 Data requirements 20 Impact of groundwater abstraction on wetlands 25 3.1 Aquifer system water balance 25 3.2 Role of wetlands in regional context 25 3.3 The effects of changes in water levels on wetland sites 26 3.4 Effect of groundwater abstraction on groundwater levels 27 3.5 Quantification of the effects of abstraction on wetland flows 30 3.6 The 10% rule 33 3.7 Relating drawdown in the aquifer to impact on the wetland water regime 34 Methodologies 41 4.1 Methodology to apply when considering an abstraction proposal 42 4.2 Impacts of current abstractions 44 4.3 Desk studies - classification of wetlands 45 4.4 Water requirements of wetlands - using a water budget model 46 Monitoring requirements and use of additional data 51 5.1 Wetland water levels 51 5.2 Local water table measurements 52 5.3 Spring flow 53 5.4 Monitoring during pumping tests 54 5.5 Incorporation of new data into existing methodologies 54 Conclusions and Recommendations 55 6.1 Introduction 55 6.2 Protection of wetlands 56 6.3 Methodologies 56 6.4 The way forward 57 Acknowledgements 59 References 61 ENVIRONMENT AGENCY 061437iniiiini Appendix A Background to Suggested Methodologies A1 Wetland water budgets, the MIROS model and the Sum Exceedance Value A2 A new well function for estimating drawdown at a wetland and induced leakage A3 Numerical modelling A4 Dimensionless groups characterising the 'drain' model Appendix B Application of methodologies to specified wetlands Appendix C Terms of Reference Executive Summary This is the final report of the Anglian Regional Operational Investigation 558 : "The Protection of East Anglian Wetlands". The objective of the project was the development of methodologies for evaluation of the likely impact of groundwater abstraction on wetland sites. The methodologies should be suitable for use at all wetland sites in East Anglia, regardless of the amount of data available for the site. A primary requirement of the methodologies is that they should indicate whether a wetland might be at risk from proposed abstractions. In the Terms of Reference, the project objective was defined in relation to the groundwater catchments of wetland sites. The project was run in two phases, and in the course of the first phase the significance of groundwater catchments in the protection of wetlands from the effects of groundwater abstraction was examined. It was concluded that identification of the groundwater catchment was not required when assessing the possibility of the wetland being adversely affected by a specific groundwater abstraction. The emphasis of the project thus changed to a consideration of wetland behaviour in response to variations in water budget, and to the effect of groundwater pumping on that water budget. The maintenance of wetlands in a low-rainfall region depends upon groundwater inputs, but groundwater is not the only important component of the water budget. In this report emphasis is placed on the construction of a simple but comprehensive water budget model, on a monthly timescale, that will predict the impact of changes in the groundwater supply on water levels in the wetland, most importantly during the summer months and in drought years. This MIROS model, which can be used for sites with no local data but can also be refined to take account of available data, has been developed in the form of a spreadsheet. Prohibition of abstractions that would cause any fall whatsoever in water levels at wetland sites is not a practical solution. For a given wetland site, predicted changes in water level and flow, resulting from a proposed groundwater abstraction, should be evaluated by an objective procedure which must recognise the water needs of plant communities. As an improvement to the simple Theis method for predicting the propagation of impacts through the aquifer, a new well function has been developed to quantify the effect of pumping on an idealised wetland. The analytical model characterises a wetland by its size, expressed as an effective radius, and a parameter which is a measure of the resistance to flow between the underlying aquifer and the wetland. Quantitative measures of the physical habitat needs of wetland plants are difficult to establish, but one approach based on field evaluation has confirmed the value of the Sum Exceedance Value (SEV) as a measure of the length and intensity of summer drought in wetland soils. The SEV can be calculated from measured or modelled water-level data on an annual or long term average basis. In this report, the combination of the MIROS model with the SEV method has been used as one means of estimating the maximum acceptable drawdown in the wetland. The results lead to a suite of methodologies which allows an assessment of the susceptibility of a wetland to a specific proposed abstraction to be made, regardless of the amount of data available. These allow more data to be used, when available, to further quantify the wetland water budget. I 1. Introduction 1.1 Background There is an abundance of definitions of a wetland, but the for the purposes of this report a wetland is defined as "an area of land whose hydrology and ecology is determined by excess water, usually in the form of a high water table giving rise to saturation or high moisture content in the root zone, and whose natural vegetation communities are dominated by plants that are adapted to these soil conditions”. Wetlands in general constitute a dwindling habitat under considerable developmental pressure. They are often protected from the effects of development by Site of Special Scientific Interest (SSSI) notification, and the presence of SSSIs is taken into account by local authorities and the National Rivers Authority (NRA) as part of the planning and licensing process. For potential threats to the conservation value of a site to outweigh the value of development, it is necessary to prove the extent of the impact of the proposed development. Environmental statements, required for some capital schemes, are often weak in the area of evaluation and prediction of potential impacts on natural systems (Boon, 1991), and it may be difficult to provide necessary scientific evidence to support unequivocal assertions relating to environmental impact on a particular site. In particular, the relationships between surface water, shallow groundwater and deep groundwater are complex and difficult to quantify. Wetlands, by their very nature, require an input of water for their survival. The amount, timing and quality of the water available control the type of wetland and the nature and diversity of the plants and animals which the wetland supports. In many cases, the need for the protection of the wetland is seen, in the first instance, as the need to protect the plant species which thrive in these environments providing a habitat for specialist animal communities, for instance wading birds, which have declined in the wider countryside. In order to adequately protect wetlands it is necessary to understand the role they play in the regional water resource environment. A long term water balance would show groundwater- fed wetlands to be areas of groundwater discharge. However, in the short term wetlands may recharge the underlying aquifer, thus maintaining groundwater levels in times of drought. In the past wetland areas in East Anglia were much more extensive than at present. Thus plant diversity could be maintained even in prolonged periods of low rainfall. Historical development, including land drainage and deepening of river channels, has reduced the wetland area present to an amount which needs careful management to ensure its conservation. The remaining areas of wetland are usually surrounded by land which has been developed, either for agricultural or urban use, and as such the wetlands are threatened by changes in agricultural and urban practices (e.g. deep drainage of fields, deepening of stream channels, diversion of runoff into storm sewers). The occurrence of wetland sites in their present positions is the result of many factors. The most difficult effect to distinguish from visual surveys is the effect of the underlying geology. It is likely that most wetlands occur where they do because of a combination of topographic, hydrological and geological features, which have subsequently been impacted by man-made 1 influences. A knowledge of the combination of features present at each site aids the understanding of the processes which are of importance for that site, and it is important that these features are correctly described. Increasing demand for new groundwater abstraction (for a variety of reasons including, for example, regional increase in demand, nitrate pollution of existing sources, and interference effects from other licensed abstractions) provides additional potential stress on wetland environments. The habitat value of wetlands is almost invariably linked to a pattern of hydrology and hydrogeochemistry that has been stable in the long term, and short term disturbances to this pattern can have important consequences to the composition and diversity of the ecosystem.
Load more

Recommended publications
  • Appropriate Assessment (Submission)
    June 2007 North Norfolk District Council Planning Policy Team Telephone: 01263 516318 E-Mail: [email protected] Write to: Jill Fisher, Planning Policy Manager, North Norfolk District Council, Holt Road, Cromer, NR27 9EN www.northnorfolk.org/ldf All of the LDF Documents can be made available in Braille, large print or in other languages. Please contact 01263 516321 to discuss your requirements. Core Strategy Appropriate Assessment (Submission) Contents 1 Introduction 4 2 The Appropriate Assessment Process 4 3 Consultation and Preparation 5 4 Evidence gathering for the Appropriate Assessment 6 European sites that may be affected 6 Characteristics and conservation objectives of the European sites 8 Other relevant plans or projects 25 5 Appropriate Assessment and Plan analysis 28 Tables Table 4.1 - Broadland SPA/SAC qualifying features 9 Table 4.2 - Great Yarmouth North Denes SPA/SAC 12 Table 4.3 - North Norfolk Coast SPA/SAC qualifying features 15 Table 4.4 - Norfolk Valley Fens SAC qualifying features 19 Table 4.5 - Overstrand Cliffs SAC qualifying features 21 Table 4.6 - Paston Great Barn SAC qualifying features 23 Table 4.7 - River Wensum SAC qualifying features 24 Table 4.8 - Neighbouring districts Core Strategy progress table 27 Table 5.1 - Screening for likely significant effects 29 Table 5.2 - Details of Settlements in policies SS1, SS3, SS5 and SS7 to SS14 and how policy amendments have resulted in no likely significant effects being identified 35 Maps Map 4.1 - Environmental Designations 7 Map 4.2 - Broadland Environmental
    [Show full text]
  • Tourism Benefit & Impacts Analysis in the Norfolk Coast Area Of
    TOURISM BENEFIT & IMPACTS ANALYSIS IN THE NORFOLK COAST AREA OF OUTSTANDING NATURAL BEAUTY APPENDICES May 2006 A Report for the Norfolk Coast Partnership Prepared by Scott Wilson NORFOLK COAST PARTNERSHIP TOURISM BENEFIT & IMPACTS ANALYSIS IN THE NORFOLK COAST AREA OF OUTSTANDING NATURAL BEAUTY APPENDICES May 2006 Prepared by Checked by Authorised by Scott Wilson Ltd 3 Foxcombe Court, Wyndyke Furlong, Abingdon Business Park, Abingdon Oxon, OX14 1DZ Tel: +44 (0) 1235 468700 Fax: +44 (0) 1235 468701 Norfolk Coast Partnership Tourism Benefit & Impacts Analysis in the Norfolk Coast AONB Scott Wilson Contents 1 A1 - Norfolk Coast Management ...............................................................1 2 A2 – Asset & Appeal Audit ......................................................................12 3 A3 - Tourism Plant Audit..........................................................................25 4 A4 - Market Context.................................................................................34 5 A5 - Economic Impact Assessment Calculations ....................................46 Norfolk Coast Partnership Tourism Benefit & Impacts Analysis in the Norfolk Coast AONB Scott Wilson Norfolk Coast AONB Tourism Impact Analysis – Appendices 1 A1 - Norfolk Coast Management 1.1 A key aspect of the Norfolk Coast is the array of authority, management and access organisations that actively participate, through one means or another, in the use and maintenance of the Norfolk Coast AONB, particularly its more fragile sites. 1.2 The aim of the
    [Show full text]
  • Fen Management Strategy - Explains the Role of the Strategy and Its Relationship to Other Documents
    CONTENTS Acknowledgements Purpose & use of the fen management strategy - explains the role of the strategy and its relationship to other documents Summary - outlines the need for a fen management strategy Introduction - Sets the picture of development and use of fens from their origins to present day Approach to producing strategy - Methodology to writing the fen management strategy Species requirements: This section provides a summary of our existing knowledge concerning birds, plants, mammals and invertebrates associated with the Broads fens. This information forms a basis for the fen management strategy. Vegetation resource Mammals Birds Invertebrates Summary of special features for each valley: This section mainly identifies the botanical features within each valley. The distribution of birds, mammals and invertebrates is either variable or unknown, and so has been covered only in a general sense in the section on species requirements. However, where there is obvious bird interest concentrated within particular valleys, this has been identified. The botanical section provides a summary analysis of the fen vegetation resource survey and considers the relative importance of fen vegetation in a local and national context. A summary of the chemical variables of the soils for each valley has also been included. Ant valley Bure valley Muckfleet valley Thurne valley Waveney valley Yare valley The fen resource for the future: Identifies aims and objectives to restore fens to favourable nature conservation state Environmental constraints and opportunities - Using the fen management strategy: - During the fen vegetation resource survey, chemical variables of the substratum associated with various plant communities were measured. The purpose of these measurements was to provide some indication of the importance of substrate to the plant communities.
    [Show full text]
  • Rights of Way Improvement Plan 2007-2017
    Norfolk County Council at your service Rights of Way Improvement Plan 2007-2017 Foreword by Cabinet Member with responsibility for Public Rights of Way Foreword I am pleased to be able to introduce There were an estimated 3.6 billion this Rights of Way Improvement Plan leisure trips to the countryside in for Norfolk 2007 - 2017. It heralds a 2005, with the average spend per trip new era extending opportunities to being £13.38. The estimated total visit the Norfolk countryside to all of value to the rural economy was £9.4 our community. billion. The Norfolk Local Access Forum, the Broads Local Access Forum, and County I see great benefit in the Council aligning Council Officers have contributed to this its major statutory transport planning plan. Significant public involvement was documents on walking, cycling, horse- secured through a consultation campaign; riding, soft-road driving, transport planning Citizens’ Panel research, and direct and health. Again, treating statutory and approaches made to disability, elderly, permissive countryside access like public ethnic, and Sure Start groups. On 20 transport, as part of the wider transport October 2004, a public conference of network, will make opportunities for interested parties discussed both the getting out and about more useful and assessment and proposed objectives. enjoyable. Enhanced management and Norfolk County Council’s countryside awareness should result from more access work has long recognised the people getting involved and sharing breadth of benefits that the service can responsibility. Understanding of the bring. Just three examples:- scope of the Council’s work, and satisfaction with it, should be boosted as Half-an-hour’s walking a day helps to the public gets directly involved in prevent high blood pressure and planning and monitoring progress.
    [Show full text]
  • Habitats Regulations Assessment of the South Norfolk Village Cluster Housing Allocations Plan
    Habitats Regulations Assessment of the South Norfolk Village Cluster Housing Allocations Plan Regulation 18 HRA Report May 2021 Habitats Regulations Assessment of the South Norfolk Village Cluster Housing Allocations Plan Regulation 18 HRA Report LC- 654 Document Control Box Client South Norfolk Council Habitats Regulations Assessment Report Title Regulation 18 – HRA Report Status FINAL Filename LC-654_South Norfolk_Regulation 18_HRA Report_8_140521SC.docx Date May 2021 Author SC Reviewed ND Approved ND Photo: Female broad bodied chaser by Shutterstock Regulation 18 – HRA Report May 2021 LC-654_South Norfolk_Regulation 18_HRA Report_8_140521SC.docx Contents 1 Introduction ...................................................................................................................................................... 1 1.2 Purpose of this report ............................................................................................................................................... 1 2 The South Norfolk Village Cluster Housing Allocations Plan ................................................................... 3 2.1 Greater Norwich Local Plan .................................................................................................................................... 3 2.2 South Norfolk Village Cluster Housing Allocations Plan ................................................................................ 3 2.3 Village Clusters ..........................................................................................................................................................
    [Show full text]
  • Circular Walks East Norfolk Coast Introduction
    National Trail 20 Circular Walks East Norfolk Coast Introduction The walks in this guide are designed to make the most of the please be mindful to keep dogs under control and leave gates as natural beauty and cultural heritage of the Norfolk coast. As you find them. companions to stretch one and two of the Norfolk Coast Path (part of the England Coast Path), they are a great way to delve Equipment deeper into this historically and naturally rich area. A wonderful Depending on the weather, some sections of these walks can array of landscapes and habitats await, many of which are be muddy. Even in dry weather, a good pair of walking boots or home to rare wildlife. The architectural landscape is expansive shoes is essential for the longer routes. Norfolk’s climate is drier too. Churches dominate, rarely beaten for height and grandeur than much of the country but unfortunately we can’t guarantee among the peaceful countryside of the coastal region, but sunshine, so packing a waterproof is always a good idea. If you there’s much more to discover. are lucky enough to have the weather on your side, don’t forget From one mile to nine there’s a walk for everyone here, whether sun cream and a hat. you’ve never walked in the countryside before or you’re a Other considerations seasoned rambler. Many of these routes lend themselves well to The walks described in these pages are well signposted on the trail running too. With the Cromer ridge providing the greatest ground, and detailed downloadable maps are available for elevation of anywhere in East Anglia, it’s a great way to get fit as each at www.norfolktrails.co.uk.
    [Show full text]
  • Rural Villages
    Rural Villages Please note that general tidying of the wording which appeared in 2019 consultation version of the draft Local Plan review will be undertaken to reflect the current situation. This will be in relation to neighbourhood plans, local services which may have changed, housing numbers, and progress of any allocations which were made by the SADMP (2106) for example: Any changes as a result of the comments revived are highlighted in Bold Comments received by Historic England (HE) and the Environment Agency (EA) are considered in separate papers Comments relating to development boundary changes are also considered in a separate paper Denver, due to comments received by the landowner/agent of the SADMP (2016) allocate site, is also considered in a separate paper dedicated to the village. Appendix A shows all the Rural Villages section with the new highlighted yellow text 1 | P a g e Table of comments for the Rural Villages Section Section Consultee(s) Nature of Summary Consultee Suggested Officer Response / Respons Modification Proposed Action e Ashwicken Mr Dale Support Provides additional support for Allocate Site H002 Due to the relatively small Hambilton Site H002 number of new homes through the draft Local Plan review required to meet the Local Housing Need (LHN) new housing allocations were not proposed to be distributed below Key Rural Service Centres. It is possible now to meet the LHN through the Local Plan review without any further housing allocations. Therefore, we will not be considering this site further in the Local Plan review. It is recommended that the consultee reviews Policy LP26 with regard to possible windfall sites.
    [Show full text]
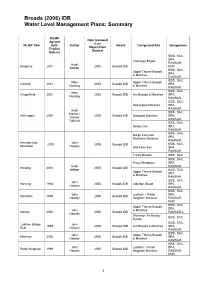
  • Broads (2006) IDB Water Level Management Plans: Summary
    Broads (2006) IDB Water Level Management Plans: Summary WLMP Date reviewed Agreed (Lou WLMP Title (with Author Board Designated Site Designation Mayer/Clive English Doarks) Nature) SSSI, SAC, SPA, Calthorpe Broad RAMSAR, Heidi Brograve 2001 2005 Broads IDB NNR Mahon SSSI, SAC, Upper Thurne Broads SPA, & Marshes RAMSAR, SSSI, SAC, Mike Upper Thurne Broads Catfield 2001 2005 Broads IDB SPA, Harding & Marshes RAMSAR, SSSI, SAC, Mike Chapelfield 2001 2005 Broads IDB Ant Broads & Marshes SPA, Harding RAMSAR, SSSI, SAC, Halvergate Marshes , SPA, RAMSAR, Heidi SSSI, SAC, Mahon / Halvergate 2000 2005 Broads IDB Damgate Marshes SPA, Sandie RAMSAR, Tolhurst SSSI, SAC, Decoy Carr , SPA, RAMSAR, SSSI, SAC, Burgh Common SPA, Muckfleet Marshes RAMSAR, Hemsby and John 2000 2005 Broads IDB SSSI, SAC, Muckfleet Harpley Hall Farm Fen SPA, RAMSAR Trinity Broads SSSI, SAC SSSI, SAC, Priory Meadows , SPA, Heidi RAMSAR, Hickling 2001 2005 Broads IDB Mahon SSSI, SAC, Upper Thurne Broads SPA, & Marshes RAMSAR, SSSI, SAC, John Horning 1998 2005 Broads IDB Alderfen Broad SPA, Harpley RAMSAR, SSSI, SAC, John Ludham – Potter SPA, Horsefen 1999 2005 Broads IDB Harpley Heigham Marshes RAMSAR, NNR SSSI, SAC, Upper Thurne Broads SPA, John & Marshes Horsey 2000 2005 Broads IDB RAMSAR,s Harpley Winterton To Horsey SSSI, SAC Dunes SSSI, SAC, Ludham Bridge John 1999 2005 Broads IDB Ant Broads & Marshes SPA, East Harpley RAMSAR, SSSI, SAC, John Upper Thurne Broads Martham 2002 2005 Broads IDB SPA, Harpley & Marshes RAMSAR, SSSI, SAC, John Ludham – Potter SPA, Potter Heigham
    [Show full text]
  • David Tyldesley and Associates Planning, Landscape and Environmental Consultants
    DAVID TYLDESLEY AND ASSOCIATES PLANNING, LANDSCAPE AND ENVIRONMENTAL CONSULTANTS Habitat Regulations Assessment: Breckland Council Submission Core Strategy and Development Control Policies Document Durwyn Liley, Rachel Hoskin, John Underhill-Day & David Tyldesley 1 DRAFT Date: 7th November 2008 Version: Draft Recommended Citation: Liley, D., Hoskin, R., Underhill-Day, J. & Tyldesley, D. (2008). Habitat Regulations Assessment: Breckland Council Submission Core Strategy and Development Control Policies Document. Footprint Ecology, Wareham, Dorset. Report for Breckland District Council. 2 Summary This document records the results of a Habitat Regulations Assessment (HRA) of Breckland District Council’s Core Strategy. The Breckland District lies in an area of considerable importance for nature conservation with a number of European Sites located within and just outside the District. The range of sites, habitats and designations is complex. Taking an area of search of 20km around the District boundary as an initial screening for relevant protected sites the assessment identified five different SPAs, ten different SACs and eight different Ramsar sites. Following on from this initial screening the assessment identifies the following potential adverse effects which are addressed within the appropriate assessment: • Reduction in the density of Breckland SPA Annex I bird species (stone curlew, nightjar, woodlark) near to new housing. • Increased levels of recreational activity resulting in increased disturbance to Breckland SPA Annex I bird species (stone curlew, nightjar, woodlark). • Increased levels of people on and around the heaths, resulting in an increase in urban effects such as increased fire risk, fly-tipping, trampling. • Increased levels of recreation to the Norfolk Coast (including the Wash), potentially resulting in disturbance to interest features and other recreational impacts.
    [Show full text]
  • 233 08 SD50 Environment Permitting Decision Document
    Environment Agency permitting decisions Bespoke permit We have decided to grant the permit for Didlington Farm Poultry Unit operated by Mr Robert Anderson, Mrs Rosamond Anderson and Mr Marcus Anderson. The permit number is EPR/EP3937EP. We consider in reaching that decision we have taken into account all relevant considerations and legal requirements and that the permit will ensure that the appropriate level of environmental protection is provided. Purpose of this document This decision document: • explains how the application has been determined • provides a record of the decision-making process • shows how all relevant factors have been taken into account • justifies the specific conditions in the permit other than those in our generic permit template. Unless the decision document specifies otherwise we have accepted the applicant’s proposals. Structure of this document • Key issues • Annex 1 the decision checklist • Annex 2 the consultation, web publicising responses. EPR/EP3937EP/A001 Page 1 of 12 Key Issues 1) Ammonia Impacts There are two Special Areas for Conservation (SAC) within 3.4km, one Special Protection Area (SPA) within 850m, seven Sites of Special Scientific Interest (SSSI) within 4.9km and six Local Wildlife Sites (LWS) within 1.4km of the facility, one of which is within 250m. Assessment of SAC and SPA If the Process Contribution (PC) is below 4% of the relevant critical level (CLe) or critical load (CLo) then the farm can be permitted with no further assessment. Initial screening using Ammonia Screening Tool (AST) v4.4 has indicated that the PC for Breckland SAC, Norfolk Valley Fens SAC and Breckland SPA is predicted to be greater than 4% of the CLe for ammonia.
    [Show full text]
  • Site Improvement Plan Norfolk Valley Fens
    Improvement Programme for England's Natura 2000 Sites (IPENS) Planning for the Future Site Improvement Plan Norfolk Valley Fens Site Improvement Plans (SIPs) have been developed for each Natura 2000 site in England as part of the Improvement Programme for England's Natura 2000 sites (IPENS). Natura 2000 sites is the combined term for sites designated as Special Areas of Conservation (SAC) and Special Protected Areas (SPA). This work has been financially supported by LIFE, a financial instrument of the European Community. The plan provides a high level overview of the issues (both current and predicted) affecting the condition of the Natura 2000 features on the site(s) and outlines the priority measures required to improve the condition of the features. It does not cover issues where remedial actions are already in place or ongoing management activities which are required for maintenance. The SIP consists of three parts: a Summary table, which sets out the priority Issues and Measures; a detailed Actions table, which sets out who needs to do what, when and how much it is estimated to cost; and a set of tables containing contextual information and links. Once this current programme ends, it is anticipated that Natural England and others, working with landowners and managers, will all play a role in delivering the priority measures to improve the condition of the features on these sites. The SIPs are based on Natural England's current evidence and knowledge. The SIPs are not legal documents, they are live documents that will be updated to reflect changes in our evidence/knowledge and as actions get underway.
    [Show full text]
  • The Norfolk & Norwich
    BRITISH MUSEUM (NATURAL HISTORY) TRANSACTIONS 2 7 JUN 1984 exchanged OF GENfcriAL LIBRARY THE NORFOLK & NORWICH NATURALISTS’ SOCIETY Edited by: P. W. Lambley Vol. 26 Part 5 MAY 1984 TRANSACTIONS OF THE NORFOLK AND NORWICH NATURALISTS’ SOCIETY Volume 26 Part 5 (May 1984) Editor P. W. Lambley ISSN 0375 7226 U: ' A M «SEUV OFFICERS OF THE SOCIETY 1984-85 j> URAL isSTORY) 2? JUH1984 President: Dr. R. E. Baker Vice-Presidents: P. R. Banham, A. Bull, K. B. Clarke, E. T. Daniels, K. C. Durrant, E. A. Ellis, R. Jones, M. J. Seago, J. A. Steers, E. L. Swann, F. J. Taylor-Page Chairman: Dr. G. D. Watts, Barn Meadow, Frost’s Lane, Gt. Moulton. Secretary: Dr. R. E. Baker, 25 Southern Reach, Mulbarton, NR 14 8BU. Tel. Mulbarton 70609 Assistant Secretary: R. N. Flowers, Heatherlands, The Street, Brundall. Treasurer: D. A. Dorling, St. Edmundsbury, 6 New Road, Heathersett. Tel. Norwich 810318 Assistant Treasurer: M. Wolner Membership Committee: R. Hancy, Tel. Norwich 860042 Miss J. Wakefield, Post Office Lane, Saxthorpe, NR1 1 7BL. Programme Committee: A. Bull, Tel. Norwich 880278 Mrs. J. Robinson, Tel. Mulbarton 70576 Publications Committee: R. Jones. P. W. Lambley & M. J. Seago (Editors) Research Committee: Dr. A. Davy, School of Biology, U.E.A., Mrs. A. Brewster Hon. Auditor. J. E. Timbers, The Nook, Barford Council: Retiring 1985; D. Fagg, J. Goldsmith, Miss F. Musters, R. Smith. Retiring 1986 Miss R. Carpenter, C. Dack, Mrs. J. Geeson, R. Robinson. Retiring 1987 N. S. Carmichael, R. Evans, Mrs.L. Evans, C. Neale Co-opted members: Dr.
    [Show full text]