Diameter and Photospheric Structures of Canopus from AMBER/VLTI Interferometry�,
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

FOR an ADVANCED Oaoi
.' ' ' > \ .\i I X-732-67-363 < I A COMPUTER, CONTROL SYSTEM I FOR AN ADVANCED OAOi ) I i I , 1 \ i J'OHN A. ,HRASTAR , P 1 (ACCESSION NUMBER) (THRU) I P > . -. c (PAGES) / + AUGUST 1967 - I . \ \ I, I \ / - k d - GO~DARD'SPACE FLIGHT CENTER ' GREENBELT, MARYLAND . .r A COMPUTER CONTROL SYSTEM FOR AN ADVANCED OAO John A. Hrastar August 1967 Goddard Space Flight Center Greenbelt, Maryland A COMPUTER CONTROL SYSTEM FOR AN ADVANCED OAO John A. Hrastar SUMMARY The purpose of the study covered by this report was to determine the feasibility of using an on-board digital computer and strap-down inertial reference unit for attitude control of an advanced OAO space- craft. An integrated, three axis control law was assumed which had been previously proven stable in the large. The principal advantage of this type of control system is the ability to complete three axis reori- entations over large angles. This system, although apparently complex, has the effect of simplifying the overall system. This is because a re- orientation is a simple extension of a hold or point operation, i.e., mode switching may be simplified. The study indicates that a system of this type is feasible and offers many advantages over present systems. The time for a reorientation using this type of control is considerably shorter than the time required using more conventional methods. The computer and inertial reference unit usedinthe study had the characteristics of systems presently under development. Feasibility, therefore is within the present state of the art, requiring only continued development of these systems. -

Luminosity - Wikipedia
12/2/2018 Luminosity - Wikipedia Luminosity In astronomy, luminosity is the total amount of energy emitted by a star, galaxy, or other astronomical object per unit time.[1] It is related to the brightness, which is the luminosity of an object in a given spectral region.[1] In SI units luminosity is measured in joules per second or watts. Values for luminosity are often given in the terms of the luminosity of the Sun, L⊙. Luminosity can also be given in terms of magnitude: the absolute bolometric magnitude (Mbol) of an object is a logarithmic measure of its total energy emission rate. Contents Measuring luminosity Stellar luminosity Image of galaxy NGC 4945 showing Radio luminosity the huge luminosity of the central few star clusters, suggesting there is an Magnitude AGN located in the center of the Luminosity formulae galaxy. Magnitude formulae See also References Further reading External links Measuring luminosity In astronomy, luminosity is the amount of electromagnetic energy a body radiates per unit of time.[2] When not qualified, the term "luminosity" means bolometric luminosity, which is measured either in the SI units, watts, or in terms of solar luminosities (L☉). A bolometer is the instrument used to measure radiant energy over a wide band by absorption and measurement of heating. A star also radiates neutrinos, which carry off some energy (about 2% in the case of our Sun), contributing to the star's total luminosity.[3] The IAU has defined a nominal solar luminosity of 3.828 × 102 6 W to promote publication of consistent and comparable values in units of https://en.wikipedia.org/wiki/Luminosity 1/9 12/2/2018 Luminosity - Wikipedia the solar luminosity.[4] While bolometers do exist, they cannot be used to measure even the apparent brightness of a star because they are insufficiently sensitive across the electromagnetic spectrum and because most wavelengths do not reach the surface of the Earth. -

The Future Life Span of Earth's Oxygenated Atmosphere
In press at Nature Geoscience The future life span of Earth’s oxygenated atmosphere Kazumi Ozaki1,2* and Christopher T. Reinhard2,3,4 1Department of Environmental Science, Toho University, Funabashi, Chiba 274-8510, Japan 2NASA Nexus for Exoplanet System Science (NExSS) 3School of Earth and Atmospheric Sciences, Georgia Institute of Technology, Atlanta, GA 30332, USA 4NASA Astrobiology Institute, Alternative Earths Team, Riverside, CA, USA *Correspondence to: [email protected] Abstract: Earth’s modern atmosphere is highly oxygenated and is a remotely detectable signal of its surface biosphere. However, the lifespan of oxygen-based biosignatures in Earth’s atmosphere remains uncertain, particularly for the distant future. Here we use a combined biogeochemistry and climate model to examine the likely timescale of oxygen-rich atmospheric conditions on Earth. Using a stochastic approach, we find that the mean future lifespan of Earth’s atmosphere, with oxygen levels more than 1% of the present atmospheric level, is 1.08 ± 0.14 billion years (1σ). The model projects that a deoxygenation of the atmosphere, with atmospheric O2 dropping sharply to levels reminiscent of the Archaean Earth, will most probably be triggered before the inception of moist greenhouse conditions in Earth’s climate system and before the extensive loss of surface water from the atmosphere. We find that future deoxygenation is an inevitable consequence of increasing solar fluxes, whereas its precise timing is modulated by the exchange flux of reducing power between the mantle and the ocean– atmosphere–crust system. Our results suggest that the planetary carbonate–silicate cycle will tend to lead to terminally CO2-limited biospheres and rapid atmospheric deoxygenation, emphasizing the need for robust atmospheric biosignatures applicable to weakly oxygenated and anoxic exoplanet atmospheres and highlighting the potential importance of atmospheric organic haze during the terminal stages of planetary habitability. -

Educator's Guide: Orion
Legends of the Night Sky Orion Educator’s Guide Grades K - 8 Written By: Dr. Phil Wymer, Ph.D. & Art Klinger Legends of the Night Sky: Orion Educator’s Guide Table of Contents Introduction………………………………………………………………....3 Constellations; General Overview……………………………………..4 Orion…………………………………………………………………………..22 Scorpius……………………………………………………………………….36 Canis Major…………………………………………………………………..45 Canis Minor…………………………………………………………………..52 Lesson Plans………………………………………………………………….56 Coloring Book…………………………………………………………………….….57 Hand Angles……………………………………………………………………….…64 Constellation Research..…………………………………………………….……71 When and Where to View Orion…………………………………….……..…77 Angles For Locating Orion..…………………………………………...……….78 Overhead Projector Punch Out of Orion……………………………………82 Where on Earth is: Thrace, Lemnos, and Crete?.............................83 Appendix………………………………………………………………………86 Copyright©2003, Audio Visual Imagineering, Inc. 2 Legends of the Night Sky: Orion Educator’s Guide Introduction It is our belief that “Legends of the Night sky: Orion” is the best multi-grade (K – 8), multi-disciplinary education package on the market today. It consists of a humorous 24-minute show and educator’s package. The Orion Educator’s Guide is designed for Planetarians, Teachers, and parents. The information is researched, organized, and laid out so that the educator need not spend hours coming up with lesson plans or labs. This has already been accomplished by certified educators. The guide is written to alleviate the fear of space and the night sky (that many elementary and middle school teachers have) when it comes to that section of the science lesson plan. It is an excellent tool that allows the parents to be a part of the learning experience. The guide is devised in such a way that there are plenty of visuals to assist the educator and student in finding the Winter constellations. -

Exploring the Brown Dwarf Desert C
Astronomy & Astrophysics manuscript no. draft c ESO 2018 March 5, 2018 MOA-2007-BLG-197: Exploring the brown dwarf desert C. Ranc1; 35, A. Cassan1; 35, M. D. Albrow2; 35, D. Kubas1; 35, I. A. Bond3; 36, V. Batista1; 35, J.-P. Beaulieu1; 35, D. P. Bennett4; 36, M. Dominik5; 35, Subo Dong6; 37, P. Fouqué7; 8; 35, A. Gould9; 37, J. Greenhilly10; 35, U. G. Jørgensen11; 35, N. Kains12; 5; 35, J. Menzies13; 35, T. Sumi14; 36, E. Bachelet15; 35, C. Coutures1; 35, S. Dieters1; 35, D. Dominis Prester16; 35, J. Donatowicz17; 35, B. S. Gaudi9; 37, C. Han18; 37, M. Hundertmark5; 11, K. Horne5; 35, S. R. Kane19; 35, C.-U. Lee20; 37, J.-B. Marquette1; 35, B.-G. Park20; 37, K. R. Pollard2; 35, K. C. Sahu12; 35, R. Street21; 35, Y. Tsapras21; 22; 35, J. Wambsganss22; 35, A. Williams23; 24; 35, M. Zub22; 35, F. Abe25; 36, A. Fukui26; 36, Y. Itow25; 36, K. Masuda25; 36, Y. Matsubara25; 36, Y. Muraki25; 36, K. Ohnishi27; 36, N. Rattenbury28; 36, To. Saito29; 36, D. J. Sullivan30; 36, W. L. Sweatman31; 36, P. J. Tristram32; 36, P. C. M. Yock33; 36, and A. Yonehara34; 36 (Affiliations can be found after the references) Received <date> / accepted <date> ABSTRACT We present the analysis of MOA-2007-BLG-197Lb, the first brown dwarf companion to a Sun-like star detected through gravitational microlensing. The event was alerted and followed-up photometrically by a network of telescopes from the PLANET, MOA, and µFUN collaborations, and observed at high angular resolution using the NaCo instrument at the VLT. -

Useful Constants
Appendix A Useful Constants A.1 Physical Constants Table A.1 Physical constants in SI units Symbol Constant Value c Speed of light 2.997925 × 108 m/s −19 e Elementary charge 1.602191 × 10 C −12 2 2 3 ε0 Permittivity 8.854 × 10 C s / kgm −7 2 μ0 Permeability 4π × 10 kgm/C −27 mH Atomic mass unit 1.660531 × 10 kg −31 me Electron mass 9.109558 × 10 kg −27 mp Proton mass 1.672614 × 10 kg −27 mn Neutron mass 1.674920 × 10 kg h Planck constant 6.626196 × 10−34 Js h¯ Planck constant 1.054591 × 10−34 Js R Gas constant 8.314510 × 103 J/(kgK) −23 k Boltzmann constant 1.380622 × 10 J/K −8 2 4 σ Stefan–Boltzmann constant 5.66961 × 10 W/ m K G Gravitational constant 6.6732 × 10−11 m3/ kgs2 M. Benacquista, An Introduction to the Evolution of Single and Binary Stars, 223 Undergraduate Lecture Notes in Physics, DOI 10.1007/978-1-4419-9991-7, © Springer Science+Business Media New York 2013 224 A Useful Constants Table A.2 Useful combinations and alternate units Symbol Constant Value 2 mHc Atomic mass unit 931.50MeV 2 mec Electron rest mass energy 511.00keV 2 mpc Proton rest mass energy 938.28MeV 2 mnc Neutron rest mass energy 939.57MeV h Planck constant 4.136 × 10−15 eVs h¯ Planck constant 6.582 × 10−16 eVs k Boltzmann constant 8.617 × 10−5 eV/K hc 1,240eVnm hc¯ 197.3eVnm 2 e /(4πε0) 1.440eVnm A.2 Astronomical Constants Table A.3 Astronomical units Symbol Constant Value AU Astronomical unit 1.4959787066 × 1011 m ly Light year 9.460730472 × 1015 m pc Parsec 2.0624806 × 105 AU 3.2615638ly 3.0856776 × 1016 m d Sidereal day 23h 56m 04.0905309s 8.61640905309 -

SAS-2019 the Symposium on Telescope Science
Proceedings for the 38th Annual Conference of the Society for Astronomical Sciences SAS-2019 The Symposium on Telescope Science Joint Meeting with the Center for Backyard Astrophysics Editors: Robert K. Buchheim Robert M. Gill Wayne Green John C. Martin John Menke Robert Stephens May, 2019 Ontario, CA i Disclaimer The acceptance of a paper for the SAS Proceedings does not imply nor should it be inferred as an endorsement by the Society for Astronomical Sciences of any product, service, method, or results mentioned in the paper. The opinions expressed are those of the authors and may not reflect those of the Society for Astronomical Sciences, its members, or symposium Sponsors Published by the Society for Astronomical Sciences, Inc. Rancho Cucamonga, CA First printing: May 2019 Photo Credits: Front Cover: NGC 2024 (Flame Nebula) and B33 (Horsehead Nebula) Alson Wong, Center for Solar System Studies Back Cover: SA-200 Grism spectrum of Wolf-Rayet star HD214419 Forrest Sims, Desert Celestial Observatory ii TABLE OF CONTENTS PREFACE v SYMPOSIUM SPONSORS vi SYMPOSIUM SCHEDULE viii PRESENTATION PAPERS Robert D. Stephens, Brian D. Warner THE SEARCH FOR VERY WIDE BINARY ASTEROIDS 1 Tom Polakis LESSONS LEARNED DURING THREE YEARS OF ASTEROID PHOTOMETRY 7 David Boyd SUDDEN CHANGE IN THE ORBITAL PERIOD OF HS 2325+8205 15 Tom Kaye EXOPLANET DETECTION USING BRUTE FORCE TECHNIQUES 21 Joe Patterson, et al FORTY YEARS OF AM CANUM VENATICORIUM 25 Robert Denny ASCOM – NOT JUST FOR WINDOWS ANY MORE 31 Kalee Tock HIGH ALTITUDE BALLOONING 33 William Rust MINIMIZING DISTORTION IN TIME EXPOSED CELESTIAL IMAGES 43 James Synge PROJECT PANOPTES 49 Steve Conard, et al THE USE OF FIXED OBSERVATORIES FOR FAINT HIGH VALUE OCCULTATIONS 51 John Martin, Logan Kimball UPDATE ON THE M31 AND M33 LUMINOUS STARS SURVEY 53 John Morris CURRENT STATUS OF “VISUAL” COMET PHOTOMETRY 55 Joe Patterson, et al ASASSN-18EY = MAXIJ1820+070 = “MAXIE”: KING OF THE BLACK HOLE 61 SUPERHUMPS Richard Berry IMAGING THE MOON AT THERMAL INFRARED WAVELENGTHS 67 iii Jerrold L. -

On the Zero Point Constant of the Bolometric Correction Scale
MNRAS 000, 1–12 () Preprint 8 March 2021 Compiled using MNRAS LATEX style file v3.0 On the Zero Point Constant of the Bolometric Correction Scale Z. Eker 1?, V. Bakış1, F. Soydugan2;3 and S. Bilir4 1Akdeniz University, Faculty of Sciences, Department of Space Sciences and Technologies, 07058, Antalya, Turkey 2Department of Physics, Faculty of Arts and Sciences, Çanakkale Onsekiz Mart University, 17100 Çanakkale, Turkey 3Astrophysics Research Center and Ulupınar Observatory, Çanakkale Onsekiz Mart University, 17100, Çanakkale, Turkey 4Istanbul University, Faculty of Science, Department of Astronomy and Space Sciences, 34119, Istanbul, Turkey ABSTRACT Arbitrariness attributed to the zero point constant of the V band bolometric correc- tions (BCV ) and its relation to “bolometric magnitude of a star ought to be brighter than its visual magnitude” and “bolometric corrections must always be negative” was investigated. The falsehood of the second assertion became noticeable to us after IAU 2015 General Assembly Resolution B2, where the zero point constant of bolometric magnitude scale was decided to have a definite value CBol(W ) = 71:197 425 ::: . Since the zero point constant of the BCV scale could be written as C2 = CBol − CV , where CV is the zero point constant of the visual magnitudes in the basic definition BCV = MBol − MV = mbol − mV , and CBol > CV , the zero point constant (C2) of the BCV scale cannot be arbitrary anymore; rather, it must be a definite positive number obtained from the two definite positive numbers. The two conditions C2 > 0 and 0 < BCV < C2 are also sufficient for LV < L, a similar case to negative BCV numbers, which means that “bolometric corrections are not always negative”. -

What's up in Space?
What’s up in Space? January 2017 Sailing the southern skies The chart is orientated for December 1 at 1am December 15 at midnight January 1 at 11pm January 15 at 10pm The constellation of Orion the hunter still dominates our Canopus is the brightest star in the constellation of Carina, eastern skies after dark. Following the line of three stars that the keel, which along with Vela, the sails, and Puppis, the mark his belt to the right you come to Sirius, or Takurua, the poop deck, once formed part of the southern constellation brightest star in our night-time sky, in the constellation of of Argo Navis, the great ship. Canis Major, Orion’s large hunting dog. There are many interesting nebulae and star clusters in Just above and to the right of Sirius, at distance of around this part of the sky, but perhaps the most famous is the 4 degrees, is M41, an open cluster of stars covering an area Eta Carinae nebula, a huge cloud of glowing gas around 7500 around the size of the full moon. It is just visible as a blurry light years away. It is one of the largest nebulae of its type smudge to the naked eye from a clear, dark location. Through in our skies (4 times the size of the Orion nebula), and the binoculars or a small telescope you will see a number of in- brightest central parts can be picked out with the naked eye. dividual stars, some showing hints of red and orange. With binoculars you should be able to see a golden star in the nebula; this is Eta Carinae, a massive, unstable star on A little further south, and set apart from the Milky Way is the the verge of blowing itself apart. -
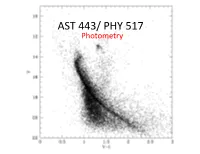
Photometry Rule of Thumb
AST 443/ PHY 517 Photometry Rule of Thumb For a uniform flux distribution, V=0 corresponds to • 3.6 x 10-9 erg cm-2 s-1 A-1 (at 5500 A = 550 nm) • 996 photons cm-2 s-1 A-1 remember: E = hn = hc/l Basic Photometry The science of measuring the brightness of an astronomical object. In principle, it is straightforward; in practice (as in much of astronomy), there are many subtleties that can cause you great pains. For this course, you do not need to deal with most of these effects, but you should know about them (especially extinction). Among the details you should be acquainted with are: • Bandpasses • Magnitudes • Absolute Magnitudes • Bolometric Fluxes and Magnitudes • Colors • Atmospheric Extinction • Atmospheric Refraction • Sky Brightness • Absolute Photometry Your detector measures the flux S in a bandpass dw. 2 2 The units of the detected flux S are erg/cm /s/A (fλ) or erg/cm /s/Hz (fν). Bandpasses Set by: • detector response, • the filter response • telescope reflectivity • atmospheric transmission Basic types of filters: • long pass: transmit light longward of some fiducial wavelength. The name of the filter often gives the 50% transmission wavelength in nm. E.g, the GG495 filter transmits 50% of the incident light at 495 nm, and has higher transmission at longer wavelengths. • short pass: transmit light shortward of some fiducial wavelength. Examples are CuSO4 and BG38. • isolating: used to select particular bandpasses. May be made of a combination of long- and short-pass filters. Narrow band filters are generally interference filters. Broadband Filters • The Johnson U,B,V bands are standard. -

• Flux and Luminosity • Brightness of Stars • Spectrum of Light • Temperature and Color/Spectrum • How the Eye Sees Color
Stars • Flux and luminosity • Brightness of stars • Spectrum of light • Temperature and color/spectrum • How the eye sees color Which is of these part of the Sun is the coolest? A) Core B) Radiative zone C) Convective zone D) Photosphere E) Chromosphere Flux and luminosity • Luminosity - A star produces light – the total amount of energy that a star puts out as light each second is called its Luminosity. • Flux - If we have a light detector (eye, camera, telescope) we can measure the light produced by the star – the total amount of energy intercepted by the detector divided by the area of the detector is called the Flux. Flux and luminosity • To find the luminosity, we take a shell which completely encloses the star and measure all the light passing through the shell • To find the flux, we take our detector at some particular distance from the star and measure the light passing only through the detector. How bright a star looks to us is determined by its flux, not its luminosity. Brightness = Flux. Flux and luminosity • Flux decreases as we get farther from the star – like 1/distance2 • Mathematically, if we have two stars A and B Flux Luminosity Distance 2 A = A B Flux B Luminosity B Distance A Distance-Luminosity relation: Which star appears brighter to the observer? Star B 2L L d Star A 2d Flux and luminosity Luminosity A Distance B 1 =2 = LuminosityB Distance A 2 Flux Luminosity Distance 2 A = A B Flux B Luminosity B DistanceA 1 2 1 1 =2 =2 = Flux = 2×Flux 2 4 2 B A Brightness of stars • Ptolemy (150 A.D.) grouped stars into 6 `magnitude’ groups according to how bright they looked to his eye. -

Habitability of the Early Earth: Liquid Water Under a Faint Young Sun Facilitated by Strong Tidal Heating Due to a Nearby Moon
Habitability of the early Earth: Liquid water under a faint young Sun facilitated by strong tidal heating due to a nearby Moon Ren´eHeller · Jan-Peter Duda · Max Winkler · Joachim Reitner · Laurent Gizon Draft July 9, 2020 Abstract Geological evidence suggests liquid water near the Earths surface as early as 4.4 gigayears ago when the faint young Sun only radiated about 70 % of its modern power output. At this point, the Earth should have been a global snow- ball. An extreme atmospheric greenhouse effect, an initially more massive Sun, release of heat acquired during the accretion process of protoplanetary material, and radioactivity of the early Earth material have been proposed as alternative reservoirs or traps for heat. For now, the faint-young-sun paradox persists as one of the most important unsolved problems in our understanding of the origin of life on Earth. Here we use astrophysical models to explore the possibility that the new-born Moon, which formed about 69 million years (Myr) after the ignition of the Sun, generated extreme tidal friction { and therefore heat { in the Hadean R. Heller Max Planck Institute for Solar System Research, Justus-von-Liebig-Weg 3, 37077 G¨ottingen, Germany E-mail: [email protected] J.-P. Duda G¨ottingenCentre of Geosciences, Georg-August-University G¨ottingen, 37077 G¨ottingen,Ger- many E-mail: [email protected] M. Winkler Max Planck Institute for Extraterrestrial Physics, Giessenbachstraße 1, 85748 Garching, Ger- many E-mail: [email protected] J. Reitner G¨ottingenCentre of Geosciences, Georg-August-University G¨ottingen, 37077 G¨ottingen,Ger- many G¨ottingenAcademy of Sciences and Humanities, 37073 G¨ottingen,Germany E-mail: [email protected] L.