DOCSLIB.ORG

Maxwell's Equations - Wikipedia, the Free Encyclopedia Page 1 of 35

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Maxwell's Equations - Wikipedia, the Free Encyclopedia Page 1 of 35 Maxwell's equations - Wikipedia, the free encyclopedia Page 1 of 35 Maxwell's equations From Wikipedia, the free encyclopedia (Redirected from Electromagnetic theory) Maxwell's equations are a set of partial differential equations Electromagnetism that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These in turn underlie modern electrical and communications technologies. Maxwell's equations have two major variants. The "microscopic" set of Maxwell's equations uses total charge and total current Electricity · Magnetism including the difficult-to-calculate atomic level charges and Electrostatics currents in materials. The "macroscopic" set of Maxwell's equations defines two new auxiliary fields that can sidestep Electric charge · Coulomb's law · having to know these 'atomic' sized charges and currents. Electric field · Electric flux · Gauss's law · Electric potential · Maxwell's equations are named after the Scottish physicist and Electrostatic induction · mathematician James Clerk Maxwell, since in an early form they Electric dipole moment · are all found in a four-part paper, "On Physical Lines of Force," which he published between 1861 and 1862. The mathematical Polarization density form of the Lorentz force law also appeared in this paper. Magnetostatics It is often useful to write Maxwell's equations in other forms; Ampère's law · Electric current · these representations are still formally termed "Maxwell's Magnetic field · Magnetization · equations". A relativistic formulation in terms of covariant field Magnetic flux · Biot–Savart law · tensors is used in special relativity, while, in quantum mechanics, Magnetic dipole moment · a version based on the electric and magnetic potentials is preferred. Gauss's law for magnetism Electrodynamics Lorentz force law · emf · Contents Electromagnetic induction · Faraday’s law · Lenz's law · ■ 1 Conceptual description Displacement current · ■ 1.1 Gauss's law Maxwell's equations · EM field · ■ 1.2 Gauss's law for magnetism Electromagnetic radiation · ■ 1.3 Faraday's law ■ 1.4 Ampère's law with Maxwell's correction Liénard–Wiechert potential · Maxwell tensor · Eddy current ■ 2 Units and summary of equations ■ 2.1 Table of 'microscopic' equations Electrical Network ■ 2.2 Table of 'macroscopic' equations Electrical conduction · ■ 2.3 Table of terms used in Maxwell's equations ■ 2.4 Proof that the two general formulations are Electrical resistance · Capacitance · equivalent Inductance · Impedance · Resonant cavities · Waveguides ■ 3 Maxwell's 'microscopic' equations ■ 3.1 With neither charges nor currents Covariant formulation ■ 4 Maxwell's 'macroscopic' equations ■ 4.1 Bound charge and current http://en.wikipedia.org/wiki/Electromagnetic_theory 5/31/2011 Maxwell's equations - Wikipedia, the free encyclopedia Page 2 of 35 ■ 4.2 Equations Electromagnetic tensor · ■ 4.3 Constitutive relations EM Stress-energy tensor · ■ 4.3.1 Without magnetic or dielectric materials Four-current · ■ 4.3.2 Isotropic Linear materials Electromagnetic four-potential ■ 4.3.3 General case Scientists ■ 4.3.4 Calculation of constitutive relations Ampère · Coulomb · Faraday · ■ 5 History ■ 5.1 Relation between electricity, magnetism, and Gauss · Heaviside · Henry · Hertz · the speed of light Lorentz · Maxwell · Tesla · Volta · ■ 5.2 The term Maxwell's equations Weber · Ørsted ■ 5.3 On Physical Lines of Force ■ 5.4 A Dynamical Theory of the Electromagnetic Field ■ 5.5 A Treatise on Electricity and Magnetism ■ 5.6 Maxwell's equations and relativity ■ 6 Modified to include magnetic monopoles ■ 7 Boundary conditions using Maxwell's equations ■ 8 Gaussian units ■ 9 Alternative formulations of Maxwell's equations ■ 9.1 Covariant formulation of Maxwell's equations ■ 9.2 Potential formulation ■ 9.3 Four-potential ■ 9.4 Differential geometric formulations ■ 9.4.1 Conceptual insight from this formulation ■ 9.5 Geometric Algebra (GA) formulation ■ 10 Classical electrodynamics as the curvature of a line bundle ■ 11 Curved spacetime ■ 11.1 Traditional formulation ■ 11.2 Formulation in terms of differential forms ■ 12 See also ■ 13 Notes ■ 14 References ■ 15 Further reading ■ 15.1 Journal articles ■ 15.2 University level textbooks ■ 15.2.1 Undergraduate ■ 15.2.2 Graduate ■ 15.2.3 Older classics ■ 15.2.4 Computational techniques ■ 16 External links ■ 16.1 Modern treatments ■ 16.2 Historical ■ 16.3 Other http://en.wikipedia.org/wiki/Electromagnetic_theory 5/31/2011 Maxwell's equations - Wikipedia, the free encyclopedia Page 3 of 35 Conceptual description Conceptually, Maxwell's equations describe how electric charges and electric currents act as sources for the electric and magnetic fields. Further, it describes how a time varying electric field generates a time varying magnetic field and vice versa. (See below for a mathematical description of these laws.) Of the four equations, two of them, Gauss's law and Gauss's law for magnetism, describe how the fields emanate from charges. (For the magnetic field there is no magnetic charge and therefore magnetic fields lines neither begin nor end anywhere.) The other two equations describe how the fields 'circulate' around their respective sources; the magnetic field 'circulates' around electric currents and time varying electric field in Ampère's law with Maxwell's correction, while the electric field 'circulates' around time varying magnetic fields in Faraday's law. Gauss's law Main article: Gauss's law Gauss's law describes the relationship between an electric field and the generating electric charges: The electric field points away from positive charges and towards negative charges. In the field line description, electric field lines begin only at positive electric charges and end only at negative electric charges. 'Counting' the number of field lines in a closed surface, therefore, yields the total charge enclosed by that surface. More technically, it relates the electric flux through any hypothetical closed "Gaussian surface" to the enclosed electric charge. Gauss's law for magnetism Main article: Gauss's law for magnetism Gauss's law for magnetism states that there are no "magnetic charges" (also called magnetic monopoles), analogous to electric charges. [1] Instead, the magnetic field due to materials is generated by a configuration called a dipole. Magnetic dipoles are best represented as loops of current but resemble positive and negative 'magnetic charges', inseparably bound together, having no net 'magnetic charge'. In terms of field lines, this equation states that magnetic field lines neither begin nor end but make loops or extend to infinity and back. In other words, any magnetic field line that enters a given volume must somewhere Gauss's law for magnetism: magnetic exit that volume. Equivalent technical statements are that the field lines never begin nor end but sum total magnetic flux through any Gaussian surface is zero, or form loops or extend to infinity as that the magnetic field is a solenoidal vector field. shown here with the magnetic field due to a ring of current. Faraday's law Main article: Faraday's law Faraday's law describes how a time varying magnetic field creates ("induces") an electric field.[1] This aspect of electromagnetic induction is the operating principle behind many electric generators: for example a rotating bar magnet creates a changing magnetic field, which in turn generates an electric http://en.wikipedia.org/wiki/Electromagnetic_theory 5/31/2011 Maxwell's equations - Wikipedia, the free encyclopedia Page 4 of 35 field in a nearby wire. (Note: there are two closely related equations which are called Faraday's law. The form used in Maxwell's equations is always valid but more restrictive than that originally formulated by Michael Faraday .) Ampère's law with Maxwell's correction Main article: Ampère's law with Maxwell's correction In a geomagnetic storm, a surge in the flux of charged particles temporarily Ampère's law with alters Earth's magnetic field, which Maxwell's correction induces electric fields in Earth's states that magnetic fields atmosphere, thus causing surges in can be generated in two our electrical power grids. ways: by electrical current (this was the original "Ampère's law") and by changing electric fields (this was "Maxwell's correction"). Maxwell's correction to Ampère's law is particularly important: It means that a changing magnetic field creates an electric field, An Wang's magnetic core memory and a changing electric field creates a magnetic field. [1][2] (1954) is an application of Ampere's Therefore, these equations allow self-sustaining "electromagnetic law. Each core stores one bit of data. waves" to travel through empty space (see electromagnetic wave equation ). The speed calculated for electromagnetic waves, which could be predicted from experiments on charges and currents, [note 1] exactly matches the speed of light; indeed, light is one form of electromagnetic radiation (as are X-rays, radio waves, and others). Maxwell understood the connection between electromagnetic waves and light in 1861, thereby unifying the previously-separate fields of electromagnetism and optics . Units and summary of equations Maxwell's equations vary with the unit system used. Though the general form remains the same, various definitions get changed and different constants appear at different places. (This may seem strange at first, but this is because some unit systems, e.g. variants of cgs, define their units in such a way that certain physical constants
Load more

Recommended publications
  • P142 Lecture 19
    P142 Lecture 19 SUMMARY Vector derivatives: Cartesian Coordinates Vector derivatives: Spherical Coordinates See Appendix A in “Introduction to Electrodynamics” by Griffiths P142 Preview; Subject Matter P142 Lecture 19 • Electric dipole • Dielectric polarization • Electric fields in dielectrics • Electric displacement field, D • Summary Dielectrics: Electric dipole The electric dipole moment p is defined as p = q d where d is the separation distance between the charges q pointing from the negative to positive charge. Lecture 5 showed that Forces on an electric dipole in E field Torque: Forces on an electric dipole in E field Translational force: Dielectric polarization: Microscopic Atomic polarization: d ~ 10-15 m Molecular polarization: d ~ 10-14 m Align polar molecules: d ~ 10-10 m Competition between alignment torque and thermal motion or elastic forces Linear dielectrics: Three mechanisms typically lead to Electrostatic precipitator Linear dielectric: Translational force: Electrostatic precipitator Extract > 99% of ash and dust from gases at power, cement, and ore-processing plants Electric field in dielectrics: Macroscopic Electric field in dielectrics: Macroscopic Polarization density P in dielectrics: Polarization density in dielectrics: Polarization density in dielectrics: The dielectric constant κe • Net field in a dielectric Enet = EExt/κe • Most dielectrics linear up to dielectric strength Volume polarization density Electric Displacement Field Electric Displacement Field Electric Displacement Field Electric Displacement Field Summary; 1 Summary; 2 Refraction of the electric field at boundaries with dielectrics Capacitance with dielectrics Capacitance with dielectrics Electric energy storage • Showed last lecture that the energy stored in a capacitor is given by where for a dielectric • Typically it is more useful to express energy in terms of magnitude of the electric field E.
    [Show full text]
  • Basic Magnetic Measurement Methods
    Basic magnetic measurement methods Magnetic measurements in nanoelectronics 1. Vibrating sample magnetometry and related methods 2. Magnetooptical methods 3. Other methods Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The unit of the magnetic flux density, Tesla (1 T=1 Wb/m2), as a derive unit of Si must be based on some measurement (force, magnetic resonance) *the alternative name is magnetic induction Introduction Magnetization is a quantity of interest in many measurements involving spintronic materials ● Biot-Savart law (1820) (Jean-Baptiste Biot (1774-1862), Félix Savart (1791-1841)) Magnetic field (the proper name is magnetic flux density [1]*) of a current carrying piece of conductor is given by: μ 0 I dl̂ ×⃗r − − ⃗ 7 1 - vacuum permeability d B= μ 0=4 π10 Hm 4 π ∣⃗r∣3 ● The Physikalisch-Technische Bundesanstalt (German national metrology institute) maintains a unit Tesla in form of coils with coil constant k (ratio of the magnetic flux density to the coil current) determined based on NMR measurements graphics from: http://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_2/2.5_halbleiterphysik_und_magnetismus/2.51/realization.pdf *the alternative name is magnetic induction Introduction It
    [Show full text]
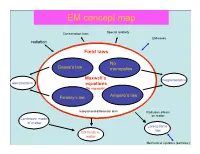
  • EM Concept Map
    EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002.
    [Show full text]
  • Implementation of the Fizeau Aether Drag Experiment for An
    Implementation of the Fizeau Aether Drag Experiment for an Undergraduate Physics Laboratory by Bahrudin Trbalic Submitted to the Department of Physics in partial fulfillment of the requirements for the degree of Bachelor of Science in Physics at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY May 2020 c Massachusetts Institute of Technology 2020. All rights reserved. ○ Author................................................................ Department of Physics May 8, 2020 Certified by. Sean P. Robinson Lecturer of Physics Thesis Supervisor Certified by. Joseph A. Formaggio Professor of Physics Thesis Supervisor Accepted by . Nergis Mavalvala Associate Department Head, Department of Physics 2 Implementation of the Fizeau Aether Drag Experiment for an Undergraduate Physics Laboratory by Bahrudin Trbalic Submitted to the Department of Physics on May 8, 2020, in partial fulfillment of the requirements for the degree of Bachelor of Science in Physics Abstract This work presents the description and implementation of the historically significant Fizeau aether drag experiment in an undergraduate physics laboratory setting. The implementation is optimized to be inexpensive and reproducible in laboratories that aim to educate students in experimental physics. A detailed list of materials, experi- mental setup, and procedures is given. Additionally, a laboratory manual, preparatory materials, and solutions are included. Thesis Supervisor: Sean P. Robinson Title: Lecturer of Physics Thesis Supervisor: Joseph A. Formaggio Title: Professor of Physics 3 4 Acknowledgments I gratefully acknowledge the instrumental help of Prof. Joseph Formaggio and Dr. Sean P. Robinson for the guidance in this thesis work and in my academic life. The Experimental Physics Lab (J-Lab) has been the pinnacle of my MIT experience and I’m thankful for the time spent there.
    [Show full text]
  • Charges and Fields of a Conductor • in Electrostatic Equilibrium, Free Charges Inside a Conductor Do Not Move
    Charges and fields of a conductor • In electrostatic equilibrium, free charges inside a conductor do not move. Thus, E = 0 everywhere in the interior of a conductor. • Since E = 0 inside, there are no net charges anywhere in the interior. Net charges can only be on the surface(s). The electric field must be perpendicular to the surface just outside a conductor, since, otherwise, there would be currents flowing along the surface. Gauss’s Law: Qualitative Statement . Form any closed surface around charges . Count the number of electric field lines coming through the surface, those outward as positive and inward as negative. Then the net number of lines is proportional to the net charges enclosed in the surface. Uniformly charged conductor shell: Inside E = 0 inside • By symmetry, the electric field must only depend on r and is along a radial line everywhere. • Apply Gauss’s law to the blue surface , we get E = 0. •The charge on the inner surface of the conductor must also be zero since E = 0 inside a conductor. Discontinuity in E 5A-12 Gauss' Law: Charge Within a Conductor 5A-12 Gauss' Law: Charge Within a Conductor Electric Potential Energy and Electric Potential • The electrostatic force is a conservative force, which means we can define an electrostatic potential energy. – We can therefore define electric potential or voltage. .Two parallel metal plates containing equal but opposite charges produce a uniform electric field between the plates. .This arrangement is an example of a capacitor, a device to store charge. • A positive test charge placed in the uniform electric field will experience an electrostatic force in the direction of the electric field.
    [Show full text]
  • The Magnetic Moment of a Bar Magnet and the Horizontal Component of the Earth’S Magnetic Field
    260 16-1 EXPERIMENT 16 THE MAGNETIC MOMENT OF A BAR MAGNET AND THE HORIZONTAL COMPONENT OF THE EARTH’S MAGNETIC FIELD I. THEORY The purpose of this experiment is to measure the magnetic moment μ of a bar magnet and the horizontal component BE of the earth's magnetic field. Since there are two unknown quantities, μ and BE, we need two independent equations containing the two unknowns. We will carry out two separate procedures: The first procedure will yield the ratio of the two unknowns; the second will yield the product. We will then solve the two equations simultaneously. The pole strength of a bar magnet may be determined by measuring the force F exerted on one pole of the magnet by an external magnetic field B0. The pole strength is then defined by p = F/B0 Note the similarity between this equation and q = F/E for electric charges. In Experiment 3 we learned that the magnitude of the magnetic field, B, due to a single magnetic pole varies as the inverse square of the distance from the pole. k′ p B = r 2 in which k' is defined to be 10-7 N/A2. Consider a bar magnet with poles a distance 2x apart. Consider also a point P, located a distance r from the center of the magnet, along a straight line which passes from the center of the magnet through the North pole. Assume that r is much larger than x. The resultant magnetic field Bm at P due to the magnet is the vector sum of a field BN directed away from the North pole, and a field BS directed toward the South pole.
    [Show full text]
  • Electromagnetism As Quantum Physics
    Electromagnetism as Quantum Physics Charles T. Sebens California Institute of Technology May 29, 2019 arXiv v.3 The published version of this paper appears in Foundations of Physics, 49(4) (2019), 365-389. https://doi.org/10.1007/s10701-019-00253-3 Abstract One can interpret the Dirac equation either as giving the dynamics for a classical field or a quantum wave function. Here I examine whether Maxwell's equations, which are standardly interpreted as giving the dynamics for the classical electromagnetic field, can alternatively be interpreted as giving the dynamics for the photon's quantum wave function. I explain why this quantum interpretation would only be viable if the electromagnetic field were sufficiently weak, then motivate a particular approach to introducing a wave function for the photon (following Good, 1957). This wave function ultimately turns out to be unsatisfactory because the probabilities derived from it do not always transform properly under Lorentz transformations. The fact that such a quantum interpretation of Maxwell's equations is unsatisfactory suggests that the electromagnetic field is more fundamental than the photon. Contents 1 Introduction2 arXiv:1902.01930v3 [quant-ph] 29 May 2019 2 The Weber Vector5 3 The Electromagnetic Field of a Single Photon7 4 The Photon Wave Function 11 5 Lorentz Transformations 14 6 Conclusion 22 1 1 Introduction Electromagnetism was a theory ahead of its time. It held within it the seeds of special relativity. Einstein discovered the special theory of relativity by studying the laws of electromagnetism, laws which were already relativistic.1 There are hints that electromagnetism may also have held within it the seeds of quantum mechanics, though quantum mechanics was not discovered by cultivating those seeds.
    [Show full text]
  • An Atomic Physics Perspective on the New Kilogram Defined by Planck's Constant
    An atomic physics perspective on the new kilogram defined by Planck’s constant (Wolfgang Ketterle and Alan O. Jamison, MIT) (Manuscript submitted to Physics Today) On May 20, the kilogram will no longer be defined by the artefact in Paris, but through the definition1 of Planck’s constant h=6.626 070 15*10-34 kg m2/s. This is the result of advances in metrology: The best two measurements of h, the Watt balance and the silicon spheres, have now reached an accuracy similar to the mass drift of the ur-kilogram in Paris over 130 years. At this point, the General Conference on Weights and Measures decided to use the precisely measured numerical value of h as the definition of h, which then defines the unit of the kilogram. But how can we now explain in simple terms what exactly one kilogram is? How do fixed numerical values of h, the speed of light c and the Cs hyperfine frequency νCs define the kilogram? In this article we give a simple conceptual picture of the new kilogram and relate it to the practical realizations of the kilogram. A similar change occurred in 1983 for the definition of the meter when the speed of light was defined to be 299 792 458 m/s. Since the second was the time required for 9 192 631 770 oscillations of hyperfine radiation from a cesium atom, defining the speed of light defined the meter as the distance travelled by light in 1/9192631770 of a second, or equivalently, as 9192631770/299792458 times the wavelength of the cesium hyperfine radiation.
    [Show full text]
  • Book of Abstracts
    Book of Abstracts 3 Foreword The 23 rd International Conference on Atomic Physics takes place in Ecole Polytechnique, a high level graduate school close to Paris. Following the tradition of ICAP, the conference presents an outstanding programme of invited VSHDNHUVFRYHULQJWKHPRVWUHFHQWVXEMHFWVLQWKH¿HOGRIDWRPLFSK\VLFVVXFKDV Ultracold gases and Bose Einstein condensates, Ultracold Fermi gases, Fundamental atomic tests and measurements, Precision measurements, atomic clocks and interferometers, Quantum information and simulations with atoms and ions, Quantum optics and cavity QED with atoms, Atoms and molecules in optical lattices, From two-body to many-body systems, Ultrafast phenomena and free electron lasers, Beyond atomic physics (biophysics, optomechanics...). The program includes 31 invited talks and 13 ‘hot topic’ talks. This book of abstracts gathers the contributions of these talks and of all posters, organized in three sessions. The proceedings of the conference will be published online in open access by the “European 3K\VLFDO-RXUQDO:HERI&RQIHUHQFHV´KWWSZZZHSMFRQIHUHQFHVRUJ On behalf of the committees, we would like to welcome you in Palaiseau, and to wish you an excit- ing conference. 4 Committees Programme committee Alain Aspect France Michèle Leduc France Hans Bachor Australia Maciej Lewenstein Spain Vanderlei Bagnato Brazil Anne L’Huillier Sweden Victor Balykin Russia Luis Orozco USA Rainer Blatt Austria Jian-Wei Pan China Denise Caldwell USA Hélène Perrin France Gordon Drake Canada Monika Ritsch-Marte Austria Wolfgang Ertmer Germany Sandro Stringari Italy Peter Hannaford Australia Regina de Vivie-Riedle Germany Philippe Grangier France Vladan Vuletic USA Massimo Inguscio Italy Ian Walmsley UK Hidetoshi Katori Japan Jun Ye USA Local organizing committee Philippe Grangier (co-chair) Institut d’Optique - CNRS Michèle Leduc (co-chair) ENS - CNRS Hélène Perrin (co-chair) U.
    [Show full text]
  • Gauss' Linking Number Revisited
    October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery.
    [Show full text]
  • Maxwell's Equations
    Maxwell’s Equations Matt Hansen May 20, 2004 1 Contents 1 Introduction 3 2 The basics 3 2.1 Static charges . 3 2.2 Moving charges . 4 2.3 Magnetism . 4 2.4 Vector operations . 5 2.5 Calculus . 6 2.6 Flux . 6 3 History 7 4 Maxwell’s Equations 8 4.1 Maxwell’s Equations . 8 4.2 Gauss’ law for electricity . 8 4.3 Gauss’ law for magnetism . 10 4.4 Faraday’s law . 11 4.5 Ampere-Maxwell law . 13 5 Conclusion 14 2 1 Introduction If asked, most people outside a physics department would not be able to identify Maxwell’s equations, nor would they be able to state that they dealt with electricity and magnetism. However, Maxwell’s equations have many very important implications in the life of a modern person, so much so that people use devices that function off the principles in Maxwell’s equations every day without even knowing it. 2 The basics 2.1 Static charges In order to understand Maxwell’s equations, it is necessary to understand some basic things about electricity and magnetism first. Static electricity is easy to understand, in that it is just a charge which, as its name implies, does not move until it is given the chance to “escape” to the ground. Amounts of charge are measured in coulombs, abbreviated C. 1C is an extraordi- nary amount of charge, chosen rather arbitrarily to be the charge carried by 6.41418 · 1018 electrons. The symbol for charge in equations is q, sometimes with a subscript like q1 or qenc.
    [Show full text]
  • Electromagnetic Field Theory
    Lecture 4 Electromagnetic Field Theory “Our thoughts and feelings have Dr. G. V. Nagesh Kumar Professor and Head, Department of EEE, electromagnetic reality. JNTUA College of Engineering Pulivendula Manifest wisely.” Topics 1. Biot Savart’s Law 2. Ampere’s Law 3. Curl 2 Releation between Electric Field and Magnetic Field On 21 April 1820, Ørsted published his discovery that a compass needle was deflected from magnetic north by a nearby electric current, confirming a direct relationship between electricity and magnetism. 3 Magnetic Field 4 Magnetic Field 5 Direction of Magnetic Field 6 Direction of Magnetic Field 7 Properties of Magnetic Field 8 Magnetic Field Intensity • The quantitative measure of strongness or weakness of the magnetic field is given by magnetic field intensity or magnetic field strength. • It is denoted as H. It is a vector quantity • The magnetic field intensity at any point in the magnetic field is defined as the force experienced by a unit north pole of one Weber strength, when placed at that point. • The magnetic field intensity is measured in • Newtons/Weber (N/Wb) or • Amperes per metre (A/m) or • Ampere-turns / metre (AT/m). 9 Magnetic Field Density 10 Releation between B and H 11 Permeability 12 Biot Savart’s Law 13 Biot Savart’s Law 14 Biot Savart’s Law : Distributed Sources 15 Problem 16 Problem 17 H due to Infinitely Long Conductor 18 H due to Finite Long Conductor 19 H due to Finite Long Conductor 20 H at Centre of Circular Cylinder 21 H at Centre of Circular Cylinder 22 H on the axis of a Circular Loop
    [Show full text]