Sensor Models
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Management of Large Sets of Image Data Capture, Databases, Image Processing, Storage, Visualization Karol Kozak
Management of large sets of image data Capture, Databases, Image Processing, Storage, Visualization Karol Kozak Download free books at Karol Kozak Management of large sets of image data Capture, Databases, Image Processing, Storage, Visualization Download free eBooks at bookboon.com 2 Management of large sets of image data: Capture, Databases, Image Processing, Storage, Visualization 1st edition © 2014 Karol Kozak & bookboon.com ISBN 978-87-403-0726-9 Download free eBooks at bookboon.com 3 Management of large sets of image data Contents Contents 1 Digital image 6 2 History of digital imaging 10 3 Amount of produced images – is it danger? 18 4 Digital image and privacy 20 5 Digital cameras 27 5.1 Methods of image capture 31 6 Image formats 33 7 Image Metadata – data about data 39 8 Interactive visualization (IV) 44 9 Basic of image processing 49 Download free eBooks at bookboon.com 4 Click on the ad to read more Management of large sets of image data Contents 10 Image Processing software 62 11 Image management and image databases 79 12 Operating system (os) and images 97 13 Graphics processing unit (GPU) 100 14 Storage and archive 101 15 Images in different disciplines 109 15.1 Microscopy 109 360° 15.2 Medical imaging 114 15.3 Astronomical images 117 15.4 Industrial imaging 360° 118 thinking. 16 Selection of best digital images 120 References: thinking. 124 360° thinking . 360° thinking. Discover the truth at www.deloitte.ca/careers Discover the truth at www.deloitte.ca/careers © Deloitte & Touche LLP and affiliated entities. Discover the truth at www.deloitte.ca/careers © Deloitte & Touche LLP and affiliated entities. -

Spatial Frequency Response of Color Image Sensors: Bayer Color Filters and Foveon X3 Paul M
Spatial Frequency Response of Color Image Sensors: Bayer Color Filters and Foveon X3 Paul M. Hubel, John Liu and Rudolph J. Guttosch Foveon, Inc. Santa Clara, California Abstract Bayer Background We compared the Spatial Frequency Response (SFR) The Bayer pattern, also known as a Color Filter of image sensors that use the Bayer color filter Array (CFA) or a mosaic pattern, is made up of a pattern and Foveon X3 technology for color image repeating array of red, green, and blue filter material capture. Sensors for both consumer and professional deposited on top of each spatial location in the array cameras were tested. The results show that the SFR (figure 1). These tiny filters enable what is normally for Foveon X3 sensors is up to 2.4x better. In a black-and-white sensor to create color images. addition to the standard SFR method, we also applied the SFR method using a red/blue edge. In this case, R G R G the X3 SFR was 3–5x higher than that for Bayer filter G B G B pattern devices. R G R G G B G B Introduction In their native state, the image sensors used in digital Figure 1 Typical Bayer filter pattern showing the alternate sampling of red, green and blue pixels. image capture devices are black-and-white. To enable color capture, small color filters are placed on top of By using 2 green filtered pixels for every red or blue, each photodiode. The filter pattern most often used is 1 the Bayer pattern is designed to maximize perceived derived in some way from the Bayer pattern , a sharpness in the luminance channel, composed repeating array of red, green, and blue pixels that lie mostly of green information. -
Cameras • Video Camera
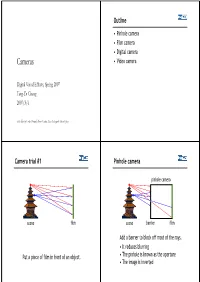
Outline • Pinhole camera •Film camera • Digital camera Cameras • Video camera Digital Visual Effects, Spring 2007 Yung-Yu Chuang 2007/3/6 with slides by Fredo Durand, Brian Curless, Steve Seitz and Alexei Efros Camera trial #1 Pinhole camera pinhole camera scene film scene barrier film Add a barrier to block off most of the rays. • It reduces blurring Put a piece of film in front of an object. • The pinhole is known as the aperture • The image is inverted Shrinking the aperture Shrinking the aperture Why not making the aperture as small as possible? • Less light gets through • Diffraction effect High-end commercial pinhole cameras Adding a lens “circle of confusion” scene lens film A lens focuses light onto the film $200~$700 • There is a specific distance at which objects are “in focus” • other points project to a “circle of confusion” in the image Lenses Exposure = aperture + shutter speed F Thin lens equation: • Aperture of diameter D restricts the range of rays (aperture may be on either side of the lens) • Any object point satisfying this equation is in focus • Shutter speed is the amount of time that light is • Thin lens applet: allowed to pass through the aperture http://www.phy.ntnu.edu.tw/java/Lens/lens_e.html Exposure Effects of shutter speeds • Two main parameters: • Slower shutter speed => more light, but more motion blur – Aperture (in f stop) – Shutter speed (in fraction of a second) • Faster shutter speed freezes motion Aperture Depth of field • Aperture is the diameter of the lens opening, usually specified by f-stop, f/D, a fraction of the focal length. -

Evaluation of the Foveon X3 Sensor for Astronomy
Evaluation of the Foveon X3 sensor for astronomy Anna-Lea Lesage, Matthias Schwarz [email protected], Hamburger Sternwarte October 2009 Abstract Foveon X3 is a new type of CMOS colour sensor. We present here an evaluation of this sensor for the detection of transit planets. Firstly, we determined the gain , the dark current and the read out noise of each layer. Then the sensor was used for observations of Tau Bootes. Finally half of the transit of HD 189733 b could be observed. 1 Introduction The detection of exo-planet with the transit method relies on the observation of a diminution of the ux of the host star during the passage of the planet. This is visualised in time as a small dip in the light curve of the star. This dip represents usually a decrease of 1% to 3% of the magnitude of the star. Its detection is highly dependent of the stability of the detector, providing a constant ux for the star. However ground based observations are limited by the inuence of the atmosphere. The latter induces two eects : seeing which blurs the image of the star, and scintillation producing variation of the apparent magnitude of the star. The seeing can be corrected through the utilisation of an adaptive optic. Yet the eect of scintillation have to be corrected by the observation of reference stars during the observation time. The perturbation induced by the atmosphere are mostly wavelength independent. Thus, record- ing two identical images but at dierent wavelengths permit an identication of the wavelength independent eects. -

ELEC 7450 - Digital Image Processing Image Acquisition
I indirect imaging techniques, e.g., MRI (Fourier), CT (Backprojection) I physical quantities other than intensities are measured I computation leads to 2-D map displayed as intensity Image acquisition Digital images are acquired by I direct digital acquisition (digital still/video cameras), or I scanning material acquired as analog signals (slides, photographs, etc.). I In both cases, the digital sensing element is one of the following: Line array Area array Single sensor Stanley J. Reeves ELEC 7450 - Digital Image Processing Image acquisition Digital images are acquired by I direct digital acquisition (digital still/video cameras), or I scanning material acquired as analog signals (slides, photographs, etc.). I In both cases, the digital sensing element is one of the following: Line array Area array Single sensor I indirect imaging techniques, e.g., MRI (Fourier), CT (Backprojection) I physical quantities other than intensities are measured I computation leads to 2-D map displayed as intensity Stanley J. Reeves ELEC 7450 - Digital Image Processing Single sensor acquisition Stanley J. Reeves ELEC 7450 - Digital Image Processing Linear array acquisition Stanley J. Reeves ELEC 7450 - Digital Image Processing Two types of quantization: I spatial: limited number of pixels I gray-level: limited number of bits to represent intensity at a pixel Array sensor acquisition I Irradiance incident at each photo-site is integrated over time I Resulting array of intensities is moved out of sensor array and into a buffer I Quantized intensities are stored as a grayscale image Stanley J. Reeves ELEC 7450 - Digital Image Processing Array sensor acquisition I Irradiance incident at each photo-site is integrated over time I Resulting array of intensities is moved out of sensor array and into a buffer I Quantized Two types of quantization: intensities are stored as a I spatial: limited number of pixels grayscale image I gray-level: limited number of bits to represent intensity at a pixel Stanley J. -

Comparison of Color Demosaicing Methods Olivier Losson, Ludovic Macaire, Yanqin Yang
Comparison of color demosaicing methods Olivier Losson, Ludovic Macaire, Yanqin Yang To cite this version: Olivier Losson, Ludovic Macaire, Yanqin Yang. Comparison of color demosaicing methods. Advances in Imaging and Electron Physics, Elsevier, 2010, 162, pp.173-265. 10.1016/S1076-5670(10)62005-8. hal-00683233 HAL Id: hal-00683233 https://hal.archives-ouvertes.fr/hal-00683233 Submitted on 28 Mar 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Comparison of color demosaicing methods a, a a O. Losson ∗, L. Macaire , Y. Yang a Laboratoire LAGIS UMR CNRS 8146 – Bâtiment P2 Université Lille1 – Sciences et Technologies, 59655 Villeneuve d’Ascq Cedex, France Keywords: Demosaicing, Color image, Quality evaluation, Comparison criteria 1. Introduction Today, the majority of color cameras are equipped with a single CCD (Charge- Coupled Device) sensor. The surface of such a sensor is covered by a color filter array (CFA), which consists in a mosaic of spectrally selective filters, so that each CCD ele- ment samples only one of the three color components Red (R), Green (G) or Blue (B). The Bayer CFA is the most widely used one to provide the CFA image where each pixel is characterized by only one single color component. -

Computer Vision, CS766
Announcement • A total of 5 (five) late days are allowed for projects. • Office hours – Me: 3:50-4:50pm Thursday (or by appointment) – Jake: 12:30-1:30PM Monday and Wednesday Image Formation Digital Camera Film Alexei Efros’ slide The Eye Image Formation • Let’s design a camera – Idea 1: put a piece of film in front of an object – Do we get a reasonable image? Steve Seitz’s slide Pinhole Camera • Add a barrier to block off most of the rays – This reduces blurring – The opening known as the aperture – How does this transform the image? Steve Seitz’s slide Camera Obscura • The first camera – 5th B.C. Aristotle, Mozi (Chinese: 墨子) – How does the aperture size affect the image? http://en.wikipedia.org/wiki/Pinhole_camera Shrinking the aperture • Why not make the aperture as small as possible? – Less light gets through – Diffraction effects... Shrinking the aperture Shrinking the aperture Sharpest image is obtained when: d 2 f d is diameter, f is distance from hole to film λ is the wavelength of light, all given in metres. Example: If f = 50mm, λ = 600nm (red), d = 0.36mm Srinivasa Narasimhan’s slide Pinhole cameras are popular Jerry Vincent's Pinhole Camera Impressive Images Jerry Vincent's Pinhole Photos What’s wrong with Pinhole Cameras? • Low incoming light => Long exposure time => Tripod KODAK Film or Paper Bright Sun Cloudy Bright TRI-X Pan 1 or 2 seconds 4 to 8 seconds T-MAX 100 Film 2 to 4 seconds 8 to 16 seconds KODABROMIDE Paper, F2 2 minutes 8 minutes http://www.kodak.com/global/en/consumer/education/lessonPlans/pinholeCamera/pinholeCanBox.shtml What’s wrong with Pinhole Cameras People are ghosted What’s wrong with Pinhole Cameras People become ghosts! Pinhole Camera Recap • Pinhole size (aperture) must be “very small” to obtain a clear image. -

2006 SPIE Invited Paper: a Brief History of 'Pixel'
REPRINT — author contact: <[email protected]> A Brief History of ‘Pixel’ Richard F. Lyon Foveon Inc., 2820 San Tomas Expressway, Santa Clara CA 95051 ABSTRACT The term pixel, for picture element, was first published in two different SPIE Proceedings in 1965, in articles by Fred C. Billingsley of Caltech’s Jet Propulsion Laboratory. The alternative pel was published by William F. Schreiber of MIT in the Proceedings of the IEEE in 1967. Both pixel and pel were propagated within the image processing and video coding field for more than a decade before they appeared in textbooks in the late 1970s. Subsequently, pixel has become ubiquitous in the fields of computer graphics, displays, printers, scanners, cameras, and related technologies, with a variety of sometimes conflicting meanings. Reprint — Paper EI 6069-1 Digital Photography II — Invited Paper IS&T/SPIE Symposium on Electronic Imaging 15–19 January 2006, San Jose, California, USA Copyright 2006 SPIE and IS&T. This paper has been published in Digital Photography II, IS&T/SPIE Symposium on Electronic Imaging, 15–19 January 2006, San Jose, California, USA, and is made available as an electronic reprint with permission of SPIE and IS&T. One print or electronic copy may be made for personal use only. Systematic or multiple reproduction, distribution to multiple locations via electronic or other means, duplication of any material in this paper for a fee or for commercial purposes, or modification of the content of the paper are prohibited. A Brief History of ‘Pixel’ Richard F. Lyon Foveon Inc., 2820 San Tomas Expressway, Santa Clara CA 95051 ABSTRACT The term pixel, for picture element, was first published in two different SPIE Proceedings in 1965, in articles by Fred C. -

Internet Engineering Dr. Marek Woda Multimedia and Computer Visualisation Part 2
Internet Engineering Dr. Marek Woda Multimedia and Computer Visualisation Part 2 Digital image Lecture Overview • Digital image, definition, acquisition • Image description • Fundamentals of image processing 1. Digital image A digital image is a two dimensional array: f = f ( x, y ) x = 0,1,2,..,N - 1; y = 0,1,2,..,M - 1 where f(x,y) - element of image (pixel), N, M - image width and hight, Element f(x,y) can have different sense e. g. - gray level, f ( x , y ) Î {0 ,1,...,S } - color, f ( x , y ) = [r( x , y ) g( x , y ) b( x , y )] r , g ,b Î {0 ,1,...,S} - color index, f ( x , y ) Î {0 ,1,...,S } 1.1. Digital camera CCD sensor ADC lens converter CFA filter memory DSP flash RAM , HD processor 1.2.1. Lens and shutter Parameters: focal length f = 20 - 300 mm, aperture F = 2.0 - 8.0 shutter 30 s. - 1/16000 s. Additional functions: ZOOM AF (Auto-focus) Viewfinder: optical LCD display 1.2.2. CCD and CFA filter CCD (Charge Coupled Device) •CCD is an analog converter •Energy of light is held as electrical charge in each photo sensor and converted to voltage 1969 - W. Boyle i G. Smith (Bell LaBs) - designed the first CCD (data storage) 1974 - Fairchild Electronics – first CCD application to image aquisition (100 x 100 px) 2015 - Canon – 250 MP sensor (19 580 x 12 600 px) How does a CCD sensor work ? Clock (serial timing) Serial Shift Register data Clock (parallel timing) light Parallel Shifting CFA filter (Color Filter Array) A Color Filter Array (CFA), is a mosaic of color filters, placed over the sensors. -

Investigation of Color Aliasing of High Spatial Frequencies and Edges for Bayer-Pattern Sensors and Foveon X3® Direct Image Sensors
Investigation of Color Aliasing of High Spatial Frequencies and Edges for Bayer-Pattern Sensors and Foveon X3® Direct Image Sensors Rudolph J. Guttosch Foveon, Inc. Santa Clara, CA Abstract The reproduction of an edge and a high frequency bar pattern is examined for image sensors employing two different color sampling technologies: Bayer RGB color filter array, and Foveon X3 solid state full color. Simulations correlate well with actual images captured using sensors representing both technologies. Color aliasing artifacts in the Bayer mosaic case depend on whether an anti-aliasing optical lowpass filter is used, and are severe without such a filter. For both the edge image and the bar pattern, the Foveon X3 direct image sensor generates few or no color aliasing artifacts associated with sampling. 1. Introduction 1.1 Bayer Background Color image data files typically viewed on computer monitors are made up of three complete planes of red, green, and blue data. Digital capture of an image with three complete planes was often accomplished with an image capture system consisting of a color separating prism and three image sensors affixed to the exit windows of the prism. Such devices produce high quality results, but require great precision in manufacturing and are costly, requiring image sensors and a prism to construct. The recent explosion of digital image capture devices in both the DSC (Digital Still Camera) and the cell phone markets has been fueled by the use of a less expensive alternative for color image capture. This alternative is known as the Bayer1 CFA (Color Filter Array), named after its inventor, Dr. -

Determining Digital Image Origin Using Sensor Imperfections
Determining Digital Image Origin Using Sensor Imperfections Jan Lukáš, Jessica Fridrich, and Miroslav Goljan Department of Electrical and Computer Engineering SUNY Binghamton, Binghamton, NY 13902-6000 ABSTRACT In this paper, we demonstrate that it is possible to use the sensor’s pattern noise for digital camera identification from images. The pattern noise is extracted from the images using a wavelet-based denoising filter. For each camera under investigation, we first determine its reference pattern, which serves as a unique identification fingerprint. This could be done using the process of flat-fielding, if we have the camera in possession, or by averaging the noise obtained from multiple images, which is the option taken in this paper. To identify the camera from a given image, we consider the reference pattern noise as a high-frequency spread spectrum watermark, whose presence in the image is established using a correlation detector. Using this approach, we were able to identify the correct camera out of 9 cameras without a single misclassification for several thousand images. Furthermore, it is possible to perform reliable identification even from images that underwent subsequent JPEG compression and/or resizing. These claims are supported by experiments on 9 different cameras including two cameras of exactly the same model. Keywords: Fixed pattern noise, digital camera identification, forensic, pattern noise, pixel non-uniformity 1. INTRODUCTION In this paper, we ask the following questions: Is it possible to find an equivalent of gun identification from bullet scratches for identification of digital cameras from images? How reliably can we distinguish between images obtained using different sensors or cameras? Is reliable identification possible from processed images? In classical film photography, there are methods for camera identification that are commonly used in forensic science. -

Sensor Superiority: It's Why the Sigma SD14 Captures the Best Color Detail
Sensor Superiority: It’s why the Sigma SD14 captures the best color detail of any DSLR! The heart of any digital camera is the image sensor—an amazing device that converts photons, bundles of light energy, into electrons, which are then collected, analyzed, and transformed into a visible image. Unlike all other digital SLRs on the market, the new Sigma SD14 incorporates a 3-layer, 14- megapixel Foveon X3 sensor that is, quite literally, cutting edge. Because this unique sensor captures full color data in all three primary colors at each pixel location, it can resolve finer details in color images than conventional sensors that only capture one color per pixel location. The result: The Sigma SD14 delivers superior real-world performance whenever you shoot high resolution pictures in color—an enormous practical edge you can easily see for yourself in comparison pictures of color test targets as well as in your own colorful digital images. What makes the SD14’s sensor better? To really understand why the Foveon X3 sensor in the Sigma SD14 is inherently superior to conventional image sensors that use a standard color filter array, let’s take a close look at how each type works. The conventional image sensor A conventional CCD or CMOS image sensor detects color by means of a specific checkerboard pattern of blue, green, and red color filters added on top of the light-sensitive silicon layer of the sensor chip at the end of the manufacturing process. As a result of this design, there is only one color filter for each pixel location.