Skew Ray Tracing in a Step-Index Optical Fiber Using Geometric Algebra
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Introduction to CODE V: Optics
Introduction to CODE V Training: Day 1 “Optics 101” Digital Camera Design Study User Interface and Customization 3280 East Foothill Boulevard Pasadena, California 91107 USA (626) 795-9101 Fax (626) 795-0184 e-mail: [email protected] World Wide Web: http://www.opticalres.com Copyright © 2009 Optical Research Associates Section 1 Optics 101 (on a Budget) Introduction to CODE V Optics 101 • 1-1 Copyright © 2009 Optical Research Associates Goals and “Not Goals” •Goals: – Brief overview of basic imaging concepts – Introduce some lingo of lens designers – Provide resources for quick reference or further study •Not Goals: – Derivation of equations – Explain all there is to know about optical design – Explain how CODE V works Introduction to CODE V Training, “Optics 101,” Slide 1-3 Sign Conventions • Distances: positive to right t >0 t < 0 • Curvatures: positive if center of curvature lies to right of vertex VC C V c = 1/r > 0 c = 1/r < 0 • Angles: positive measured counterclockwise θ > 0 θ < 0 • Heights: positive above the axis Introduction to CODE V Training, “Optics 101,” Slide 1-4 Introduction to CODE V Optics 101 • 1-2 Copyright © 2009 Optical Research Associates Light from Physics 102 • Light travels in straight lines (homogeneous media) • Snell’s Law: n sin θ = n’ sin θ’ • Paraxial approximation: –Small angles:sin θ~ tan θ ~ θ; and cos θ ~ 1 – Optical surfaces represented by tangent plane at vertex • Ignore sag in computing ray height • Thickness is always center thickness – Power of a spherical refracting surface: 1/f = φ = (n’-n)*c -

Depth of Focus (DOF)
Erect Image Depth of Focus (DOF) unit: mm Also known as ‘depth of field’, this is the distance (measured in the An image in which the orientations of left, right, top, bottom and direction of the optical axis) between the two planes which define the moving directions are the same as those of a workpiece on the limits of acceptable image sharpness when the microscope is focused workstage. PG on an object. As the numerical aperture (NA) increases, the depth of 46 focus becomes shallower, as shown by the expression below: λ DOF = λ = 0.55µm is often used as the reference wavelength 2·(NA)2 Field number (FN), real field of view, and monitor display magnification unit: mm Example: For an M Plan Apo 100X lens (NA = 0.7) The depth of focus of this objective is The observation range of the sample surface is determined by the diameter of the eyepiece’s field stop. The value of this diameter in 0.55µm = 0.6µm 2 x 0.72 millimeters is called the field number (FN). In contrast, the real field of view is the range on the workpiece surface when actually magnified and observed with the objective lens. Bright-field Illumination and Dark-field Illumination The real field of view can be calculated with the following formula: In brightfield illumination a full cone of light is focused by the objective on the specimen surface. This is the normal mode of viewing with an (1) The range of the workpiece that can be observed with the optical microscope. With darkfield illumination, the inner area of the microscope (diameter) light cone is blocked so that the surface is only illuminated by light FN of eyepiece Real field of view = from an oblique angle. -

Super-Resolution Imaging by Dielectric Superlenses: Tio2 Metamaterial Superlens Versus Batio3 Superlens
hv photonics Article Super-Resolution Imaging by Dielectric Superlenses: TiO2 Metamaterial Superlens versus BaTiO3 Superlens Rakesh Dhama, Bing Yan, Cristiano Palego and Zengbo Wang * School of Computer Science and Electronic Engineering, Bangor University, Bangor LL57 1UT, UK; [email protected] (R.D.); [email protected] (B.Y.); [email protected] (C.P.) * Correspondence: [email protected] Abstract: All-dielectric superlens made from micro and nano particles has emerged as a simple yet effective solution to label-free, super-resolution imaging. High-index BaTiO3 Glass (BTG) mi- crospheres are among the most widely used dielectric superlenses today but could potentially be replaced by a new class of TiO2 metamaterial (meta-TiO2) superlens made of TiO2 nanoparticles. In this work, we designed and fabricated TiO2 metamaterial superlens in full-sphere shape for the first time, which resembles BTG microsphere in terms of the physical shape, size, and effective refractive index. Super-resolution imaging performances were compared using the same sample, lighting, and imaging settings. The results show that TiO2 meta-superlens performs consistently better over BTG superlens in terms of imaging contrast, clarity, field of view, and resolution, which was further supported by theoretical simulation. This opens new possibilities in developing more powerful, robust, and reliable super-resolution lens and imaging systems. Keywords: super-resolution imaging; dielectric superlens; label-free imaging; titanium dioxide Citation: Dhama, R.; Yan, B.; Palego, 1. Introduction C.; Wang, Z. Super-Resolution The optical microscope is the most common imaging tool known for its simple de- Imaging by Dielectric Superlenses: sign, low cost, and great flexibility. -

To Determine the Numerical Aperture of a Given Optical Fiber
TO DETERMINE THE NUMERICAL APERTURE OF A GIVEN OPTICAL FIBER Submitted to: Submitted By: Mr. Rohit Verma 1. Rajesh Kumar 2. Sunil Kumar 3. Varun Sharma 4. Jaswinder Singh INDRODUCTION TO AN OPTICAL FIBER Optical fiber: an optical fiber is a dielectric wave guide made of glass and plastic which is used to guide and confine an electromagnetic wave and work on the principle to total internal reflection (TIR). The diameter of the optical fiber may vary from 0.05 mm to 0.25mm. Construction Of An Optical Fiber: (Where N1, N2, N3 are the refractive indexes of core, cladding and sheath respectively) Core: it is used to guide the electromagnetic waves. Located at the center of the cable mainly made of glass or sometimes from plastics it also as the highest refractive index i.e. N1. Cladding: it is used to reduce the scattering losses and provide strength t o the core. It has less refractive index than that of the core, which is the main cause of the TIR, which is required for the propagation of height through the fiber. Sheath: it is the outer most coating of the optical fiber. It protects the core and clad ding from abrasion, contamination and moisture. Requirement for making an optical fiber: 1. It must be possible to make long thin and flexible fiber using that material 2. It must be transparent at a particular wavelength in order for the fiber to guide light efficiently. 3. Physically compatible material of slightly different index of refraction must be available for core and cladding. -

Numerical Aperture of a Plastic Optical Fiber
International Journal of Innovations in Engineering and Technology (IJIET) Numerical Aperture of A Plastic Optical Fiber Trilochan Patra Assistant professor, Department of Electronics and Communication Engineering Techno India College of Technology, Rajarhat, Newtown, Kolkata-156, West Bengal, India Abstract: - To use plastic optical fibers it is useful to know their numerical apertures. These fibers have a large core diameter, which is very different from those of glass fibers. For their connection a strict adjustment to the properties of the optical systems is needed, injecting the light inside and collecting it outside so as not to increase the losses resulting of their strong absorption. If it is sufficient to inject the light at the input with an aperture lower than the theoretical aperture without core stopping, it is very useful to know the out numerical aperture which is varying with the injection aperture and the length of the fiber, because the different modes may be not coupled and are not similarly absorbed. Here I propose a method of calculating numerical aperture by calculating acceptance angle of the fiber. Experimental result shows that we measure the numerical aperture by calculating the mean diameter and then the radius of the spot circle projected on a graph paper. We also measure the distance of the fiber from the target (graph paper). Then make a ratio between the radius of the spot circle and the distance. From here we calculate the acceptance angle and then numerical aperture by sin of acceptance angle. I. INTRODUCTION In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. -

Diffraction Notes-1
Diffraction and the Microscope Image Peter Evennett, Leeds [email protected] © Peter Evennett The Carl Zeiss Workshop 1864 © Peter Evennett Some properties of wave radiation • Beams of light or electrons may be regarded as electromagnetic waves • Waves can interfere: adding together (in certain special circumstances): Constructive interference – peaks correspond Destructive interference – peaks and troughs • Waves can be diffracteddiffracted © Peter Evennett Waves radiating from a single point x x Zero First order First Interference order order between waves radiating from Second Second two points order order x and x x x © Peter Evennett Zero Interference order between waves radiating from two more- First First order order closely-spaced points x and x xx Zero First order First Interference order order between waves radiating from Second Second two points order order x and x x x © Peter Evennett Z' Y' X' Image plane Rays rearranged according to origin Back focal plane Rays arranged -2 -1 0 +1 +2 according to direction Objective lens Object X Y Z © Peter Evennett Diffraction in the microscope Diffraction grating Diffraction pattern in back focal plane of objective © Peter Evennett What will be the As seen in the diffraction pattern back focal plane of this grating? of the microscope in white light © Peter Evennett Ernst Abbe’s Memorial, Jena February1994 © Peter Evennett Ernst Abbe’s Memorial, Jena Minimum d resolved distance Wavelength of λ imaging radiation α Half-aperture angle n Refractive index of medium Numerical Aperture Minimum resolved distance is now commonly expressed as d = 0.61 λ / NA © Peter Evennett Abbe’s theory of microscopical imaging 1. -

Page 1 Magnification/Reduction Numerical Aperture
CHE323/CHE384 Chemical Processes for Micro- and Nanofabrication www.lithoguru.com/scientist/CHE323 Diffraction Review Lecture 43 • Diffraction is the propagation of light in the presence of Lithography: boundaries Projection Imaging, part 1 • In lithography, diffraction can be described by Fraunhofer diffraction - the diffraction pattern is the Fourier Transform Chris A. Mack of the mask transmittance function • Small patterns diffract more: frequency components of Adjunct Associate Professor the diffraction pattern are inversely proportional to dimensions on the mask Reading : Chapter 7, Fabrication Engineering at the Micro- and Nanoscale , 4 th edition, Campbell • For repeating patterns (such as a line/space array), the diffraction pattern becomes discrete diffracted orders • Information about the pitch is contained in the positions of the diffracted orders, and the amplitude of the orders determines the duty cycle (w/p) © 2013 by Chris A. Mack www.lithoguru.com © Chris Mack 2 Fourier Transform Examples Fourier Transform Properties g(x) Graph of g(x) G(f ) = x F{g ( x , y )} G(,) fx f y 1,x < 0.5 sin(π f ) rect() x = x > π 0,x 0.5 f x From Fundamental 1,x > 0 1 i Principles of Optical step() x = δ ()f − 0,x < 0 x π + = + Lithography , by 2 2 fx Linearity: F{(,)af x y bg( x , y )} aF(,) fx f y bG(,) fx f y Chris A. Mack (Wiley & Sons, 2007) Delta function δ ()x 1 − π + − − = i2 ( fx a f y b) Shift Theorem: F{(g x a, y b)} G(,) f f e ∞ ∞ x y ()=δ − δ − comb x ∑ ()x j ∑ ()fx j j =−∞ j =−∞ 1 1 1 1 π δ + +δ − f cos( x) fx fx -

The F-Word in Optics
The F-word in Optics F-number, was first found for fixing photographic exposure. But F/number is a far more flexible phenomenon for finding facts about optics. Douglas Goodman finds fertile field for fixes for frequent confusion for F/#. The F-word of optics is the F-number,* also known as F/number, F/#, etc. The F- number is not a natural physical quantity, it is not defined and used consistently, and it is often used in ways that are both wrong and confusing. Moreover, there is no need to use the F-number, since what it purports to describe can be specified rigorously and unambiguously with direction cosines. The F-number is usually defined as follows: focal length F-number= [1] entrance pupil diameter A further identification is usually made with ray angle. Referring to Figure 1, a ray from an object at infinity that is parallel to the axis in object space intersects the front principal plane at height Y and presumably leaves the rear principal plane at the same height. If f is the rear focal length, then the angle of the ray in image space θ′' is given by y tan θ'= [2] f In this equation, as in the others here, a sign convention for angles heights and magnifications is not rigorously enforced. Combining these equations gives: 1 F−= number [3] 2tanθ ' For an object not at infinity, by analogy, the F-number is often taken to be the half of the inverse of the tangent of the marginal ray angle. However, Eq. 2 is wrong. -
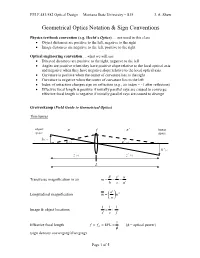
Geometrical Optics Notation & Sign Conventions
EELE 481/582 Optical Design Montana State University – S15 J. A. Shaw Geometrical Optics Notation & Sign Conventions Physics textbook convention (e.g. Hecht’s Optics) … not used in this class Object distances are positive to the left, negative to the right Image distances are negative to the left, positive to the right Optical engineering convention …what we will use Directed distances are positive to the right, negative to the left Angles are positive when they have positive slope relative to the local optical axis and negative when they have negative slope relative to the local optical axis. Curvature is positive when the center of curvature lies to the right Curvature is negative when the center of curvature lies to the left Index of refraction changes sign on reflection (e.g., air index = -1 after reflection) Effective focal length is positive if initially parallel rays are caused to converge; effective focal length is negative if initially parallel rays are caused to diverge Greivenkamp (Field Guide to Geometrical Optics) Thin lenses object n f n΄ image space space h (+) u (+) u΄ (-) h΄ (-) z (-) z΄ (+) L h' z' u Transverse magnification in air m h z u' n' Longitudinal magnification m m2 n 1 1 1 Image & object locations z' z f 1 Effective focal length f f EFL ( = optical power) E (sign denotes converging/diverging) Page 1 of 5 EELE 481/582 Optical Design Montana State University – S15 J. A. Shaw n Front focal length (directed distance) f nf F E n' Rear focal length (directed distance) f ' n' f R E f f ' Effective focal length from front or rear focal lengths f F R E n n' ☼ Note: the front and rear focal lengths are directed distances (signs determined by direction), but the effective focal length is not (its sign is determined by whether the surface or element causes incoming parallel rays to converge or diverge). -

Diffractive Flat Lens Enables Extreme Depth-Of-Focus Imaging
Diffractive flat lens enables extreme depth-of-focus imaging Sourangsu Banerji,1 Monjurul Meem, 1 Apratim Majumder, 1 Berardi Sensale-Rodriguez1 and Rajesh Menon1, 2, a) 1Department of Electrical and Computer Engineering, University of Utah, Salt Lake City, UT 84112, USA. 2Oblate Optics, Inc. San Diego CA 92130, USA. a) [email protected] ABSTRACT A lens performs an approximately one-to-one mapping from the object to the image planes. This mapping in the image plane is maintained within a depth of field (or referred to as depth of focus, if the object is at infinity). This necessitates refocusing of the lens when the images are separated by distances larger than the depth of field. Such refocusing mechanisms can increase the cost, complexity and weight of imaging systems. Here, we show that by judicious design of a multi- level diffractive lens (MDL) it is possible to drastically enhance the depth of focus, by over 4 orders of magnitude. Using such a lens, we are able to maintain focus for objects that are separated by as large as ~6m in our experiments. Specifically, when illuminated by collimated light at l=0.85mm, the MDL produced a beam that remained in focus from 5mm to ~1500mm from the MDL. The measured full-width at half-maximum of the focused beam varied from 6.6µm (5mm away from MDL) to 524µm (1500mm away from MDL). Since the sidelobes were well suppressed and the main-lobe was close to the diffraction-limit, imaging with a horizontal X vertical field of view of 20o x 15o over the entire focal range was demonstrated. -

Chapter 7 Lenses
Chapter 7 Lenses Chapter 7 Lenses © C. Robert Bagnell, Jr., Ph.D., 2012 Lenses are the microscope’s jewels. Understanding their properties is critical in understanding the microscope. Objective, condenser, and eyepiece lenses have information about their properties inscribed on their housings. Table 7.1 is an example from objective lenses. This chapter will unfold the meaning and significance of these symbols. The three main categories of information are Numerical Aperture, Magnification / Tube Length, and Aberration Corrections. Zeiss Leitz Plan-Apochromat 170/0.17 63X/1.40 Oil Pl 40 / 0.65 ∞/0.17 Nikon Olympus Fluor 20 Ph3 ULWD CDPlan 40PL 0.75 0.50 160/0.17 160/0-2 Table 7.1 – Common Objective Lens Inscriptions Numerical Aperture & Resolution Figure 7.1 Inscribed on every objective lens and most 3 X condenser lenses is a number that indicates the lenses N.A. 0.12 resolving power – its numerical aperture or NA. For the Zeiss lens in table 7.1 it is 1.40. The larger the NA the better the resolving power. Ernst Abbe invented the concept of numerical aperture in 1873. However, prior to Abbe’s quantitative formulation of resolving power other people, such as Charles Spencer, intuitively understood the underlying principles and had used them to produce 1 4˚ superior lenses. Spencer and Angular Aperture 95 X So, here is a bit about Charles Spencer. In the mid N.A. 1.25 1850's microscopists debated the relationship of angular aperture to resolution. Angular aperture is illustrated in 110˚ Pathology 464 Light Microscopy 1 Chapter 7 Lenses figure 7.1. -

Advanced Microscopy Training
Microscopy Training & Overview Product Marketing October 2011 Stephan Briggs - PLE OVERVIEW AND PRESENTATION FLOW • Glossary and Important Terms • Introduction – Timeline – Innovation and Advancement – Primary Components • Edmund Optics Product Offering • Illumination Techniques • Microscopy Techniques – Brightfield – Darkfield – Phase Contrast • Microscope Objectives – Finite Conjugate – Infinity Corrected 2 PROPRIETARY - Property of Edmund Optics, Inc. | 2011 Copyright© Edmund Optics, Inc. GLOSSARY AND IMPORTANT TERMS 3 • Numerical Aperture (NA) Function of the focal length and entrance pupil diameter. NA determines resolving power, depth of field, and contrast of the image. The higher the NA, the greater the resolving power and smaller the depth of field. NA can be calculated using Equation 1. NA = n*Sinθ Equation 1 Where n is the index of refraction of the medium in which the lens is working (n=1.0 for air) and θ is the half-angle of the maximum cone of light that can enter or exit the lens. • Resolving Power (R) Minimum distance between points or lines that are just distinguishable as separate entities. The resolving power of a system is determined by N.A. and wavelength of light (λ), as shown in Equation 2. R = 0.61*λ /N.A. Equation 2 • Working Distance (WD) Distance between the surface of the specimen and the front face of the objective when in focus PROPRIETARY - Property of Edmund Optics, Inc. | 2011 Copyright© Edmund Optics, Inc. GLOSSARY AND IMPORTANT TERMS 4 • Parfocal Length Distance between the surface of the specimen and the objective mounting position when in focus. • Infinity Corrected Optical System An optical system in which the image is formed by an objective and a tube lens with an Infinity Space between them, into which optical accessories can be inserted.