The Modulated Low-Temperature Structure of Malayaite, Casnosio4
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Synthesis, Properties and Uses of Chromium-Based Pigments from The
Synthesis, properties and uses of chromium-based pigments from the Manufacture de Sèvres Louisiane Verger, Olivier Dargaud, Mathieu Chassé, Nicolas Trcera, Gwenaëlle Rousse, Laurent Cormier To cite this version: Louisiane Verger, Olivier Dargaud, Mathieu Chassé, Nicolas Trcera, Gwenaëlle Rousse, et al.. Syn- thesis, properties and uses of chromium-based pigments from the Manufacture de Sèvres. Journal of Cultural Heritage, Elsevier, 2018, 30, pp.26 - 33. 10.1016/j.culher.2017.09.012. hal-01777923 HAL Id: hal-01777923 https://hal.sorbonne-universite.fr/hal-01777923 Submitted on 25 Apr 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Synthesis, Properties and Uses of Chromium-Based Pigments from the Manufacture de Sèvres Louisiane Verger1,2, Olivier Dargaud2, Mathieu Chassé1, Nicolas Trcera3, Gwenaëlle Rousse4,5, Laurent Cormier1 1. Institut de minéralogie, de physique des matériaux et de cosmochimie (IMPMC), Sorbonne Universités, UPMC Univ Paris 06, CNRS UMR 7590, Muséum national d'Histoire naturelle, IRD UMR 206, 4 place Jussieu, F-75005 Paris, France 2. Cité de la céramique - Sèvres et Limoges, 2 Place de la Manufacture, 92310 Sèvres, France 3. Synchrotron Soleil, 91190 Saint-Aubin 4 .Collège de France, Chimie du Solide et de l’Energie, UMR 8260, 11 place Marcelin Berthelot, 75231 Paris Cedex 05, France. -

Malayaite Casnsio5 C 2001 Mineral Data Publishing, Version 1.2 ° Crystal Data: Monoclinic
Malayaite CaSnSiO5 c 2001 Mineral Data Publishing, version 1.2 ° Crystal Data: Monoclinic. Point Group: 2=m: Crystals wedge-shaped, up to 3 cm; massive, as a coating on cassiterite. Physical Properties: Hardness = 3.5{4 D(meas.) = 4.3(2) D(calc.) = [4.55] Fluoresces pale to bright yellow or yellow-green under UV. Optical Properties: Translucent. Color: Very pale creamy yellow to deep yellow-orange, colorless. Luster: Resinous. Optical Class: Biaxial ({). ® = 1.764{1.765 ¯ = 1.783{1.786 ° = 1.798{1.801 2V(meas.) = 84±{86± Cell Data: Space Group: A2=a: a = 7.156(6) b = 8.895(9) c = 6.668(4) ¯ = 113:4(1)± Z = 4 X-ray Powder Pattern: Synthetic. 3.28 (100), 5.05 (50), 2.639 (45), 3.06 (35), 2.665 (30), 2.412 (20), 2.099 (20) Chemistry: (1) (2) SiO2 21.26 22.49 SnO2 58.48 56.38 FeO 0.15 CaO 19.14 20.94 LOI 0.50 Total 99.38 99.96 (1) Sungei Lah Valley, Malaya; corresponds to Ca0:95Sn1:07Si0:98O5: (2) Gumble, Australia; by electron microprobe, corresponding to Ca1:00Sn1:00Fe0:01Si1:00O5: Occurrence: In tin-rich contact metamorphic skarn deposits, probably a hydrothermal alteration product of cassiterite or other tin-bearing minerals. Association: Cassiterite, quartz, calcite, wollastonite, pyroxene, garnet. Distribution: In the Sungei Lah Valley, Chenderiang, Perak State, and other locations in Malaya, Malaysia. From Piniok, Thailand. In the Toroku and Mitate mines, Miyazaki Prefecture; the Sampo mine, Okayama Prefecture; the Hoei mine, Oita Prefecture; and the Kuga mine, Yamaguchi Prefecture, Japan. -

O, a New Mineral of the Titanite Group from the Piława Górna Pegmatite, the Góry Sowie Block, Southwestern Poland
Mineralogical Magazine, June 2017, Vol. 81(3), pp. 591–610 Żabińskiite, ideally Ca(Al0.5Ta 0.5)(SiO4)O, a new mineral of the titanite group from the Piława Górna pegmatite, the Góry Sowie Block, southwestern Poland 1,* 2 3 3 4 ADAM PIECZKA ,FRANK C. HAWTHORNE ,CHI MA ,GEORGE R. ROSSMAN ,ELIGIUSZ SZEŁĘG , 5 5 6 6 7 ADAM SZUSZKIEWICZ ,KRZYSZTOF TURNIAK ,KRZYSZTOF NEJBERT ,SŁAWOMIR S. ILNICKI ,PHILIPPE BUFFAT AND 7 BOGDAN RUTKOWSKI 1 AGH University of Science and Technology, Department of Mineralogy, Petrography and Geochemistry, 30-059 Kraków, Mickiewicza 30, Poland 2 Department of Geological Sciences, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada 3 Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, 91125-2500, California, USA 4 University of Silesia, Faculty of Earth Sciences, Department of Geochemistry, Mineralogy and Petrography, 41-200 Sosnowiec, Bedzin̨ ská 60, Poland 5 University of Wrocław, Institute of Geological Sciences, 50-204 Wrocław, M. Borna 9, Poland 6 University of Warsaw, Faculty of Geology, Institute of Geochemistry, Mineralogy and Petrology, 02-089 Warszawa, Żwirki and Wigury 93, Poland 7 AGH University of Science and Technology, International Centre of Electron Microscopy for Materials Science, Department of Physical and Powder Metallurgy, 30-059 Kraków, Mickiewicza 30, Poland [Received 7 January 2016; Accepted 21 April 2016; Associate Editor: Ed Grew] ABSTRACT Ż ́ ł abinskiite, ideally Ca(Al0.5Ta0.5)(SiO4)O, was found in a Variscan granitic pegmatite at Pi awa Górna, Lower Silesia, SW Poland. The mineral occurs along with (Al,Ta,Nb)- and (Al,F)-bearing titanites, a pyrochlore-supergroup mineral and a K-mica in compositionally inhomogeneous aggregates, ∼120 μm× 70 μm in size, in a fractured crystal of zircon intergrown with polycrase-(Y) and euxenite-(Y). -

Structural Investigations Along the Join Catiosio4-Casnosio4
Structural investigations along the join CaTiOSiO4-CaSnOSiO4 Autor(en): Kunz, Martin / Xirouchakis, Dimitros / Wang, Yanbin Objekttyp: Article Zeitschrift: Schweizerische mineralogische und petrographische Mitteilungen = Bulletin suisse de minéralogie et pétrographie Band (Jahr): 77 (1997) Heft 1 PDF erstellt am: 05.10.2021 Persistenter Link: http://doi.org/10.5169/seals-58464 Nutzungsbedingungen Die ETH-Bibliothek ist Anbieterin der digitalisierten Zeitschriften. Sie besitzt keine Urheberrechte an den Inhalten der Zeitschriften. Die Rechte liegen in der Regel bei den Herausgebern. Die auf der Plattform e-periodica veröffentlichten Dokumente stehen für nicht-kommerzielle Zwecke in Lehre und Forschung sowie für die private Nutzung frei zur Verfügung. Einzelne Dateien oder Ausdrucke aus diesem Angebot können zusammen mit diesen Nutzungsbedingungen und den korrekten Herkunftsbezeichnungen weitergegeben werden. Das Veröffentlichen von Bildern in Print- und Online-Publikationen ist nur mit vorheriger Genehmigung der Rechteinhaber erlaubt. Die systematische Speicherung von Teilen des elektronischen Angebots auf anderen Servern bedarf ebenfalls des schriftlichen Einverständnisses der Rechteinhaber. Haftungsausschluss Alle Angaben erfolgen ohne Gewähr für Vollständigkeit oder Richtigkeit. Es wird keine Haftung übernommen für Schäden durch die Verwendung von Informationen aus diesem Online-Angebot oder durch das Fehlen von Informationen. Dies gilt auch für Inhalte Dritter, die über dieses Angebot zugänglich sind. Ein Dienst der ETH-Bibliothek ETH Zürich, Rämistrasse 101, 8092 Zürich, Schweiz, www.library.ethz.ch http://www.e-periodica.ch SCHWEIZ. MINERAL. PETROGR. MITE 77, 1-11,1997 Structural investigations along the join CaTi0Si04-CaSn0Si04 by Martin Kunz', Dimitrios Xirouchakis2, Yanbin Wang3, John B. Parise2 and Donald H. Lindsley2 Abstract High resolution synchrotron X-ray data were used to structurally characterize a series of compounds along the sol- id-solution titanite (HT-phase)-malayaite. -

Titanite (Sphene) Outline Crystal Structure of Titanite
Titanite (Sphene) CaTiO(SiO4) By Dominic Papineau and Tiffany Yesavage Titanite refers to titanium which was named after the Titans, the mythical first sons of the Earth. Outline 1 Chemical composition 2 Physical properties 3 Optical properties 4 Crystal structure 5 Titanite stability 6 Occurrences 7 Uses Crystal structure of titanite Ca polyhedron Ti octahedron Si tetrahedron O atoms 1 Chemical substitutions In Titanium octahedra: Most commonly Al3+ or Fe3+ replaces Ti4+. Occasionally, Fe2+ and REE such as Nb5+ and Ta5+ may also substitute for Ti4+ . For Oxygen: O2- is commonly replaced by either F- or OH-. The most common substitution that occurs in titanite involves this coupled substitution: (Al,Fe)3+ + O2- >> Ti4+ + (OH-, F -) Notice that the above charges balance. This particular substitution may occur in up to 30% of cations in titanite. Chemical substitutions (continued) For Calcium: Sr, Ba, Na, Mn and REE such as Ce and Nd may substitute for Ca2+ . U, Th and radiogenic Pb may also substitute for Calcium. Like zircon and apatite, titanite may be used in order to determine the ages of rocks. In the Silica tetrahedra: The only element observed to substitute for Si4+ is Al3+ . A complete solid solution has also been shown to exist between o CaTiO(SiO4) and SnTiO(SiO4) at 700 C and 7kbar. SnTiO(SiO4) is the chemical composition of malayaite. Malayaite and the high temperature form of titanite are they are isostructural. Physical properties Color: gray, brown, green, yellow, black, transparent to translucent Luster: resinous to adamantine Cleavage: {110} distinct Hardness: 5 - 5.5 Because of titanite’s lack of hardness, it weathers quickly in most rocks Specific gravity: 3.4 - 3.55 2 Optical properties Titanite under thin section can be determined from its “sphenoidal shape” as seen in a thin section. -
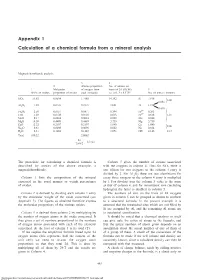
Appendix 1 Calculation of a Chemical Formula from a Mineral Analysis
Appendix 1 Calculation of a chemical formula from a mineral analysis Appendix 1 Magnesiohornblende analysis 3 4 2 Atomic proportion No. of anions on 1 Molecular of oxygen from basis of 24 (O,OH) 5 Wt.% of oxides proportion of oxides each molecule i.e. col. 368.3735 No. of ions in formula SiO 51.63 0.8594 1.7188 14.392 Si 7.196 2 8.00 0.804 } Al2O3 7.39 0.0725 0.2175 1.821 Al 1.214 0.410 3+ Fe2O3 2.50 0.0157 0.0471 0.394 Fe 0.263 FeO 5.30 0.0738 0.0738 0.618 Fe2+ 0.618 5.07 MnO 0.17 0.0024 0.0024 0.020 Mn 0.020 } MgO 18.09 0.4489 0.4489 3.759 Mg 3.759 CaO 12.32 0.2197 0.2197 1.840 Ca 1.840 2.00 Na2O 0.61 0.0098 0.0098 0.082 Na 0.164 } H2O+ 2.31 0.1282 0.1282 1.073 OH 2.146 2.15 Total 100.32 2.8662 24 = 8.3735 2.8662 The procedure for calculating a chemical formula is Column 5 gives the number of cations associated described by means of the above example, a with the oxygens in column 4. Thus for SiO2 there is magnesiohornblende. one silicon for two oxygens so the column 4 entry is divided by 2. For A12O3 there are two aluminiums for Column 1 lists the composition of the mineral every three oxygens so the column 4 entry is multiplied expressed in the usual manner as weight percentages by ~˜. -

Malayaite Ceramic Pigments: a Combined Optical Spectroscopy and Neutron/X-Ray Diffraction Study
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by PUblication MAnagement Published on the Materials Research Bulletin, 44 (2009) 1778-1785. Copyright © 2009 Elsevier Ltd. All rights reserved. doi: 10.1016/j.materresbull.2009.03.006 Malayaite Ceramic Pigments: a Combined Optical Spectroscopy and Neutron/X-ray Diffraction Study Giuseppe Cruciani1, Michele Dondi2, Matteo Ardit1, Teodora Stoyanova Lyubenova3, Juan B. Carda3, Francesco Matteucci2, Anna L. Costa2 1Department of Earth Sciences, University of Ferrara, Via Saragat 1, 44100 Ferrara, Italy 2ISTEC-CNR, Institute of Science and Technology for Ceramics, Via Granarolo 64, 48018 Faenza, Italy 3Dept of Inorganic and Organic Chemistry, University Jaime I, Campus Riu Sec, 12071 Castellón, Spain Abstract. Ceramic pigments based on the Cr-doped malayaite structure were synthesized by solid state reaction and characterized by optical spectroscopy and combined X-ray and neutron powder diffraction in order to elucidate the still unclear chromium substitution mechanisms. The results show that coloration is actually due to simultaneous occurrence of Cr4+ and Cr3+ ions in the crystal lattice. Spectroscopy data confirm that Cr4+ is replacing Sn4+ in the octahedral site and, in minor amount, Si4+ in the tetrahedral site. In addition, neutron powder diffraction data suggest that Cr3+ substitution for octahedral Sn4+ is charge balanced by formation of oxygen vacancies with no preference over the different oxygen sites. Upon incorporation of Cr ion, the SnO6 octahedra exhibit an off-centre displacement of central cation which in turn induces a rearrangement of both the octahedral and tetrahedral coordination shells. Key-words: ceramic pigment, crystal structure, malayaite, neutron diffraction, optical spectroscopy, X-ray diffraction. -
![Arxiv:1204.3007V2 [Cond-Mat.Mtrl-Sci] 23 Oct 2012 Thermal Changes in Molecular Conformation; And, Third, the High-Pressure Form of The](https://docslib.b-cdn.net/cover/3360/arxiv-1204-3007v2-cond-mat-mtrl-sci-23-oct-2012-thermal-changes-in-molecular-conformation-and-third-the-high-pressure-form-of-the-7363360.webp)
Arxiv:1204.3007V2 [Cond-Mat.Mtrl-Sci] 23 Oct 2012 Thermal Changes in Molecular Conformation; And, Third, the High-Pressure Form of The
1 PASCal: A principal-axis strain calculator for thermal expansion and compressibility determination Matthew J. Cliffe and Andrew L. Goodwin * Department of Chemistry, University of Oxford, Inorganic Chemistry Laboratory, South Parks Road, Oxford, OX1 3QR U.K.. E-mail: [email protected] (Received 0 XXXXXXX 0000; accepted 0 XXXXXXX 0000) Abstract We describe a web-based tool (pascal; principal axis strain calculator, http://pascal.chem.ox.ac.uk) designed to simplify the determination of principal coefficients of thermal expansion and compressibilities from variable-temperature and variable-pressure lattice param- eter data. In a series of three case studies, we use pascal to re-analyse previously- published lattice parameter data and show that additional scientific insight is obtain- able in each case. First, the two-dimensional metal{organic framework Cu-SIP-3 is found to exhibit the strongest area-negative thermal expansion (NTE) effect yet observed; second, the widely-used explosive HMX exhibits much stronger mechanical anisotropy than had previously been anticipated, including uniaxial NTE driven by arXiv:1204.3007v2 [cond-mat.mtrl-sci] 23 Oct 2012 thermal changes in molecular conformation; and, third, the high-pressure form of the mineral malayaite is shown to exhibit a strong negative linear compressibility (NLC) effect that arises from correlated tilting of SnO6 and SiO4 coordination polyhedra. PREPRINT: Journal of Applied Crystallography A Journal of the International Union of Crystallography 2 1. Introduction The mechanisms by which crystalline materials respond to changes in temperature and pressure are as important for the valuable insight they provide into the funda- mental chemistry of the solid state as they are for a range of practical applications. -

A Synchrotron Radiation, HRTEM, X-Ray Powder Diffraction, and Raman Spectroscopic Study of Malayaite, Casnsios
American Mineralogist, Volume 81, pages 595-602, 1996 A synchrotron radiation, HRTEM, X-ray powder diffraction, and Raman spectroscopic study of malayaite, CaSnSiOs LEE A. GROAT,! STEFAN KEK,2 ULRICH BISMAYER,3 CLAUDIA SCHMIDT,4 HANS GEORG KRANE,s HINRICH MEYER,3 LEONA NISTOR,6 AND GUSTAAF VAN TENDELOO6 IDepartment of Geological Sciences, University of British Columbia, Vancouver, British Columbia V6T 1Z4, Canada 2FR Kristallographie, Universitat des Saarlandes, D-66041 Saarbriicken, Germany 3Mineralogisch-Petrographisches Institut, Universitat Hamburg, D-20146 Hamburg, Germany 4Institut fUr Mineralogie, Universitat, Welfengarten I, D-30060 Hanover, Germany 'Institut fUr Kristallographie, Universitat, Kaiserstrasse 12, D-76128 Karlsruhe, Germany .Universiteit Antwerpen (RUCA), Groenenborgerlaan 171, B-2020 Antwerp, Belgium ABSTRACT Synchrotron radiation, high-resolution transmission electron microscopy (HRTEM), X-ray powder diffraction, and Raman spectroscopy were used to study the structure and thermal behavior of malayaite, CaSnSiO,. No indications of deviation from A21a sym- metry and no structural transitions were observed between 100 and 870 K. HRTEM revealed that the material is free of domains and antiphase boundaries. However, the lattice constants, cell volume, and Raman-active phonons show a thermal discontinuity near 500 K, which is possibly related to variation of the coordination sphere around the highly anisotropic Ca position. INTRODUCTION rameter (Salje et al. 1993a). In perfect agreement with observations by Zhang et al. (1995), Kek et al. (1994) Malayaite, CaSnSiO" is a rare mineral found in skarn recently showed that in synthetic titanite between 850 deposits. The structure of malayaite was solved by Hig- and 496 K the Ca atoms are displaced parallel to a and gins and Ribbe (1977) in space group A21a and was re- c, so that the true symmetry of the intermediate regime fined to R = 4.7% from data collected with conventional is P2/n. -

A Synchrotron Radiation, HRTEM, X-Ray Powder Diffraction
American Mineralogist, Volume 81, pages 595-602, 1996 A synchrotronradiation, HRTEM, X-ray powder diffraction, and Raman spectroscopicstudy of malayaite, CaSnSiOt Lnn A. Gnoerrl SrnrlN Knn 2 Ur,nrcn Brstv.lyonr3 Clnuorl Scunnrotra H,lNs Gnonc Kru.Nnr5 HrNnrcn MEyERr3 LnoN,l NrsroRr6 lNo Gusralr VaN TrNonr,oo6 'Department of Geological Sciences,University of British Columbia, Vancouver, British ColumbiaY6T lZ4, Canada 'zFRKristallographie, Universidt des Saarlandes,D-66041 Saarbriicken,Germany 3Mineralogisch-PetrographischesInstitut, Universitlit Hamburg, D-20I46 Hamburg, Germany 4lnstitut {iir Mineralogie, Universitiit, Welfengarten l, D-30060 Hanover, Germany 5lnstitut fiir Kristallographie, Universidt, Kaiserstrasse12, D-76128 Karlsruhe, Germany 6Universiteit Antwerpen (RUCA), Groenenborgerlaan17 I , B-2020 Antwerp, Belgium AssrRAcr Synchrotron radiation, high-resolution transmission electron microscopy (HRTEM), X-ray powder diffraction, and Raman spectroscopywere used to study the structure and thermal behavior of malayaite, CaSnSiOr. No indications of deviation from A2/a sym- metry and no structural transitions were observed between 100 and 870 K. HRTEM revealed that the material is free of domains and antiphase boundaries. However, the lattice constants,cell volume, and Raman-active phonons show a thermal discontinuity near 500 K, which is possibly related to variation of the coordination spherearound the highly anisotropic Ca position. IxrnooucrroN rameter (Saljeet al. 1993a).In perfect agreementwith observationsby Zhang et al. (1995), Kek et al. (199a) Malayaite, CaSnSiOr,is a rare mineral found in skarn recently showed that in synthetic titanite between 850 deposits.The structure of malayaite was solved by Hig- and 496 K the Ca atoms are displaced parallel to a and gins and Ribbe (1977) in spacegroup A2/a and was re- c, so that the true symmetry of the intermediate regime fined to R: 4.'lo/ofrom data collectedwith conventional is P2r/n. -

New Mineral Names*
American Mineralogist, Volume 67, pages 854-860, 1982 NEW MINERAL NAMES* Arsenocrandallite* Although single-crystal X-ray diffraction study showed no departure from cubic symmetry, the burtite unit cell is consid- Kurt Walenta (1981) Minerals of the beudantite-crandallite group ered to be rhombohedral with spacegroup RT, a, = 8. 128~, = from the Black Forest: Arsenocrandallite and sulfate-free 900, = (a = 11.49, = 14.08A in hexagonal setting). The weilerite. Schweiz. Mineralog. Petrog. Mitt., 61, 23-35 (in strongest lines in the X-ray powder diffraction pattern are (in A, German). for CoKa, indexing is based on the pseudo-cubic cell): Microprobe analysis gave As205 22.9, P20J 10.7, AI2O3 28.7, 4.06(vs)(200), 1.814(~)(420),1.657(~)(422), 0.9850(~)(820,644) and Fez03 1.2, CaO 6.9, SrO 6.0, BaO 4.3, CuO 1.8, ZnO 0.3, Biz03 0.9576(~)(822,660). 2.4, Si02 3.2, H20 (loss on ignition) 11.7, sum 100.1% cor- Electron microprobe analysis (with H20calculated to provide responding to (C~O.~IS~~.~~B~O.14Bio.0~)~.09(A12.79C~~. I Feo'& the stoichiometric quantity of OH) gave Sn02 56.3, CaO 20.6, Zn0.02)2.99 (As0.99 p0.7~ Si0.26)2.00 H6.44 013.63, Or MgO 0.3, H20 20.2, total 97.4 wt.%. These data give an (Ca,Sr)Al3H[(As,P)O4I2(0H),.Spectrographic analysis showed empirical formula of (Cao.9s2Mgo.020)Zl.oo2Sno.999(OH)6or, ideal- small amounts of Na, K, and C1. A second sample is nearly free ly, Casn(OH)6. -

Photoluminescence of Synthetic Titanite-Group Pigments: a Rare Quenching Effect
See discussions, stats, and author profiles for this publication at: http://www.researchgate.net/publication/262195479 Photoluminescence of synthetic titanite-group pigments: A rare quenching effect ARTICLE in CHEMIE DER ERDE - GEOCHEMISTRY · OCTOBER 2014 Impact Factor: 1.4 · DOI: 10.1016/j.chemer.2014.04.004 DOWNLOADS VIEWS 59 78 8 AUTHORS, INCLUDING: Teodora Stoyanova Lyubenova Michael Gaft Universitat Jaume I Laser Distance Spectrometry, Israel 27 PUBLICATIONS 50 CITATIONS 84 PUBLICATIONS 1,079 CITATIONS SEE PROFILE SEE PROFILE Dominik Talla University of Vienna 13 PUBLICATIONS 16 CITATIONS SEE PROFILE Available from: Teodora Stoyanova Lyubenova Retrieved on: 21 July 2015 provided by Repositori Institucional de la Universitat Jaume I View metadata, citation and similar papers at core.ac.uk CORE brought to you by G Model CHEMER-25311; No. of Pages 6 ARTICLE IN PRESS Chemie der Erde xxx (2014) xxx–xxx Contents lists available at ScienceDirect Chemie der Erde j ournal homepage: www.elsevier.de/chemer Photoluminescence of synthetic titanite-group pigments: A rare quenching effect a,∗ b c a Lutz Nasdala , Teodora Stoyanova Lyubenova , Michael Gaft , Manfred Wildner , d a e a Wilfredo Diegor , Christian Petautschnig , Dominik Talla , Christoph Lenz a Institut für Mineralogie und Kristallographie, Universität Wien, Althanstr. 14, A-1090 Wien, Austria b Departament de Química Inorgànica i Orgànica, University Jaume I, 12071 Castellón de la Plana, Spain c OLDS Laser Distance Spectrometry Ltd., Petah-Tikva 49528, Israel d Department of Earth Sciences, Memorial University of Newfoundland, St. John’s, NL A1B 3X5, Canada e Institute of Geological Sciences, Masaryk University, 61137 Brno, Czech Republic a r t i c l e i n f o a b s t r a c t Article history: Chromium-doped titanite and malayaite samples, which were synthesised to evaluate their performance Received 21 October 2013 as ceramic pigments, show remarkable photoluminescence behaviour.