An Application for Detecting Bias in Spider Solitaire Programs 1 Introduction 2 Random Walks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(“Spider-Man”) Cr
PRIVILEGED ATTORNEY-CLIENT COMMUNICATION EXECUTIVE SUMMARY SECOND AMENDED AND RESTATED LICENSE AGREEMENT (“SPIDER-MAN”) CREATIVE ISSUES This memo summarizes certain terms of the Second Amended and Restated License Agreement (“Spider-Man”) between SPE and Marvel, effective September 15, 2011 (the “Agreement”). 1. CHARACTERS AND OTHER CREATIVE ELEMENTS: a. Exclusive to SPE: . The “Spider-Man” character, “Peter Parker” and essentially all existing and future alternate versions, iterations, and alter egos of the “Spider- Man” character. All fictional characters, places structures, businesses, groups, or other entities or elements (collectively, “Creative Elements”) that are listed on the attached Schedule 6. All existing (as of 9/15/11) characters and other Creative Elements that are “Primarily Associated With” Spider-Man but were “Inadvertently Omitted” from Schedule 6. The Agreement contains detailed definitions of these terms, but they basically conform to common-sense meanings. If SPE and Marvel cannot agree as to whether a character or other creative element is Primarily Associated With Spider-Man and/or were Inadvertently Omitted, the matter will be determined by expedited arbitration. All newly created (after 9/15/11) characters and other Creative Elements that first appear in a work that is titled or branded with “Spider-Man” or in which “Spider-Man” is the main protagonist (but not including any team- up work featuring both Spider-Man and another major Marvel character that isn’t part of the Spider-Man Property). The origin story, secret identities, alter egos, powers, costumes, equipment, and other elements of, or associated with, Spider-Man and the other Creative Elements covered above. The story lines of individual Marvel comic books and other works in which Spider-Man or other characters granted to SPE appear, subject to Marvel confirming ownership. -

By Roland Barthes and "La Carte Postale" by Jacques Derrida
Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1995 Re: (Writing) Desire in "Fragments d'Un Discours Amoureux" by Roland Barthes and "La Carte Postale" by Jacques Derrida. Laura Elizabeth Volpe Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Volpe, Laura Elizabeth, "Re: (Writing) Desire in "Fragments d'Un Discours Amoureux" by Roland Barthes and "La Carte Postale" by Jacques Derrida." (1995). LSU Historical Dissertations and Theses. 6141. https://digitalcommons.lsu.edu/gradschool_disstheses/6141 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master, UMX films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps. -
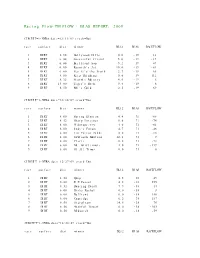
Racing Flow-TM FLOW + BIAS REPORT: 2009
Racing Flow-TM FLOW + BIAS REPORT: 2009 CIRCUIT=1-NYRA date=12/31/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 5.50 Hollywood Hills 0.0 -19 13 2 DIRT 6.00 Successful friend 5.0 -19 -19 3 DIRT 6.00 Brilliant Son 5.2 -19 47 4 DIRT 6.00 Raynick's Jet 10.6 -19 -61 5 DIRT 6.00 Yes It's the Truth 2.7 -19 65 6 DIRT 8.00 Keep Thinking 0.0 -19 -112 7 DIRT 8.32 Storm's Majesty 4.0 -19 6 8 DIRT 13.00 Tiger's Rock 9.4 -19 6 9 DIRT 8.50 Mel's Gold 2.5 -19 69 CIRCUIT=1-NYRA date=12/30/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.00 Spring Elusion 4.4 71 -68 2 DIRT 8.32 Sharp Instinct 0.0 71 -74 3 DIRT 6.00 O'Sotopretty 4.0 71 -61 4 DIRT 6.00 Indy's Forum 4.7 71 -46 5 DIRT 6.00 Ten Carrot Nikki 0.0 71 -18 6 DIRT 8.00 Sawtooth Moutain 12.1 71 9 7 DIRT 6.00 Cleric 0.6 71 -73 8 DIRT 6.00 Mt. Glittermore 4.0 71 -119 9 DIRT 6.00 Of All Times 0.0 71 0 CIRCUIT=1-NYRA date=12/27/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.50 Quip 4.5 -38 49 2 DIRT 6.00 E Z Passer 4.2 -38 255 3 DIRT 8.32 Dancing Daisy 7.9 -38 14 4 DIRT 6.00 Risky Rachel 0.0 -38 8 5 DIRT 6.00 Kaffiend 0.0 -38 150 6 DIRT 6.00 Capridge 6.2 -38 187 7 DIRT 8.50 Stargleam 14.5 -38 76 8 DIRT 8.50 Wishful Tomcat 0.0 -38 -203 9 DIRT 8.50 Midwatch 0.0 -38 -59 CIRCUIT=1-NYRA date=12/26/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 6.00 Papaleo 7.0 108 129 2 DIRT 6.00 Overcommunication 1.0 108 -72 3 DIRT 6.00 Digger 0.0 108 -211 4 DIRT 6.00 Bryan Kicks 0.0 108 136 5 DIRT 6.00 We Get It 16.8 108 129 6 DIRT 6.00 Yawanna Trust 4.5 108 -21 7 DIRT 6.00 Smarty Karakorum 6.5 108 83 8 DIRT 8.32 Almighty Silver 18.7 108 133 9 DIRT 8.32 Offlee Cool 0.0 108 -60 CIRCUIT=1-NYRA date=12/13/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.32 Crafty Bear 3.0 -158 -139 2 DIRT 6.00 Cheers Darling 0.5 -158 61 3 DIRT 6.00 Iberian Gate 3.0 -158 154 4 DIRT 6.00 Pewter 0.5 -158 8 5 DIRT 6.00 Wolfson 6.2 -158 86 6 DIRT 6.00 Mr. -

Adventuring with Books: a Booklist for Pre-K-Grade 6. the NCTE Booklist
DOCUMENT RESUME ED 311 453 CS 212 097 AUTHOR Jett-Simpson, Mary, Ed. TITLE Adventuring with Books: A Booklist for Pre-K-Grade 6. Ninth Edition. The NCTE Booklist Series. INSTITUTION National Council of Teachers of English, Urbana, Ill. REPORT NO ISBN-0-8141-0078-3 PUB DATE 89 NOTE 570p.; Prepared by the Committee on the Elementary School Booklist of the National Council of Teachers of English. For earlier edition, see ED 264 588. AVAILABLE FROMNational Council of Teachers of English, 1111 Kenyon Rd., Urbana, IL 61801 (Stock No. 00783-3020; $12.95 member, $16.50 nonmember). PUB TYPE Books (010) -- Reference Materials - Bibliographies (131) EDRS PRICE MF02/PC23 Plus Postage. DESCRIPTORS Annotated Bibliographies; Art; Athletics; Biographies; *Books; *Childress Literature; Elementary Education; Fantasy; Fiction; Nonfiction; Poetry; Preschool Education; *Reading Materials; Recreational Reading; Sciences; Social Studies IDENTIFIERS Historical Fiction; *Trade Books ABSTRACT Intended to provide teachers with a list of recently published books recommended for children, this annotated booklist cites titles of children's trade books selected for their literary and artistic quality. The annotations in the booklist include a critical statement about each book as well as a brief description of the content, and--where appropriate--information about quality and composition of illustrations. Some 1,800 titles are included in this publication; they were selected from approximately 8,000 children's books published in the United States between 1985 and 1989 and are divided into the following categories: (1) books for babies and toddlers, (2) basic concept books, (3) wordless picture books, (4) language and reading, (5) poetry. (6) classics, (7) traditional literature, (8) fantasy,(9) science fiction, (10) contemporary realistic fiction, (11) historical fiction, (12) biography, (13) social studies, (14) science and mathematics, (15) fine arts, (16) crafts and hobbies, (17) sports and games, and (18) holidays. -

Information to Users
INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps. Each original is also photographed in one exposure and is included in reduced form at the back of the book. Photographs included in the original manuscript have been reproduced xerographically in this copy. Higher quality 6” x 9” black and white photographic prints are available for any photographs or illustrations appearing in this copy for an additional charge. Contact UMI directly to order. UMI A Beil & Howell Information Company 300 North Zeeb Road, Arm Arbor MI 48106-1346 USA 313/761-4700 800/521-0600 THE RANDOLPH SLAVE SAGA: COMMUNITIES IN COLLISION DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of the Ohio State University By Ross Frederick Bagby, M.A. -

The Remarkable History of Sir Thomas Upmore, Bart., Mp, Formerly Known As
THE REMARKABLE HISTORY OF SIR THOMAS UPMORE, BART., M.P., FORMERLY KNOWN AS "TOMMY UPMORE" R. D. BLACKMORE CHAPTER I. SIGNS OF EMINENCE. If I know anything of mankind, one of them needs but speak the truth to secure the attention of the rest, amazed as they are at a feat so far beyond their own power and experience. And I would not have troubled any one's attention, if I could only have been let alone, and not ferreted as a phenomenon. When the facts, which I shall now relate, were fresh and vivid in the public mind, it might have been worth twenty guineas to me to set them in order and publish them. Such curiosity, then, was felt, and so much of the purest science talked, about my "abnormal organism," that nine, or indeed I may say ten, of the leading British publishers went so far as to offer me £20,[ with a chance of five dollars from America, if I would only write my history! But when a man is in full swing of his doings and his sufferings, how can he stop to set them down, for the pleasure of other people? And even now, when, if I only tried, I could do almost as much as ever, it is not with my own consent that you get this narrative out of me. How that comes to pass, you shall see hereafter. Every one who knows me will believe that I have no desire to enlarge a fame, which already is too much for me. -

Buried Alive Cambridge Loca the Sir A
i.i "i.. ■ ■ ' ■ •' ■ ■ •! ■■ .: TWELVE PAGES. By Appointment to i ■i.' I His Majesty tbe King, Her Majesty the Queen, CURTAINS. Her Majesty Queen Alexandra. For every winjdow in the House i • . ^ j 2f000 pairs ^ select from, i The London Dyers & Cl'eaners, 2/1 l i to 30/- per pair. C L E A N &• i D Y E In a HIGHLY SATISFAeTOB^ M.ANNEU; I ■ ( (1) Ladies’ Dresses, Blouses and Sports-Coats. ' ' r)‘ ■! (2) ' Gentlemen’s Suits and Overcoats. t - i ' 1 ; \flNALLS'; ■. r 3) Hcusehold'Draperies and Curtains. Ji- 'j . ■. Tlhe Popular Price Draper! IE S t JIECUI jATION. L a r g e s t O l d e s t E STABLISHED. 12, Su sse x Ga r d e n s, ’TERMijNus R d ., ii. 'F-. - b ’ l-i_________ [I” EASTBOURNE Hi? . : ' T elep h o n e—1161.' TERMINUS ROAD. R e g is t e r e d at t h H Q.P.O; , P P J T ('JTT,' QA No. 3,19d " frZnd Olf PUBLI CATION W EDN EbDAY); M AY 29, 191$. AS A.NEWSPApin. A AnlVi. BURIED ALIVE CAMBRIDGE LOCA THE SIR A. CALLAGHAN. TO THE SOUTH POLE. TOMMY THE-NEW LIBERAL CANDIDATE AND FUNERAL SERVl PRIZE-GIVING ON RENEWAL OF, LICENSE S r R E R N E S T S K A C KL E T 0 N REFUSED. DESCRIBES HIS EXPEDITION. a*: STUDIES NATURE IN FRANCE. AN INDUSTRIAL CAREER. THE M. IVOR’S ADVICE. OFFICER’S AMA: COMPENSATION QUESTION As announced in! oUr last issue Sir Alfred A WONDERFUL STORY. -

Texas Summer Yearling and Mixed Sale
TEXAS SUMMER YEARLING AND MIXED SALE AUGUST 27, 2018 AT 12 NOON TEXAS THOROUGHBRED SALES PAVILION Lone Star Park at Grand Prairie Sponsored by the Texas Thoroughbred Association www.texasthoroughbred.com www.ttasales.com Texas Summer Yearling and Mixed Sale Sponsored by the Texas Thoroughbred Association August 27, 2018 at 12 noon To be sold at public auction at Lone Star Park, 1000 Lone Star Parkway Grand Prairie, Texas Auctioneers – Walt Robertson #11624 Bruce McCarty #11698 Announcer – Dave Appleton The upset price is $1,000 for any horse in this catalogue. Day of Sale Phone: 972-237-4886 Day of Sale FAX: 972-237-5257 1000 Lone Star Parkway • Grand Prairie,Texas 75050 Tim Boyce, Sales Director: 972-523-0332 TTA Office: 512-458-6133 • Fax: 512-453-5919 www.texasthoroughbred.com Contents Authorization of Agent. 5 Buyer & Agent Information ......................6 Buyer Application ..............................7 Notices. 8 Black Type Race Definitions ....................10 Texas Thoroughbred Association ................13 Texas Thoroughbred Association Directors . 14 Accredited Texas-bred Program .................15 Accredited Texas-bred Program Rules and Fees ....16 Texas Sales Futurity/ Texas Stallion Stakes ..........................17 TTA Membership Application . 19 State Organizations/Stakes Info. 21 Sales Area Map. 23 Area Accommodations .........................24 Repository ...................................26 Conditions of Sale . 38 SALES INDICES Consignors Index .............................27 Sires Index ...................................32 Dams Index. 33 State-Foaled Index ............................35 Authorization of Agent Please complete entire form and mail to: 192 Cimarron Park Loop, Suite A Buda, TX 78610 Date: ____/____/____ Tel: 512.458.6133 • Fax: 512.453.5919 Gentlemen: I hereby appoint __________________________ to be my authorized agent in all matters pertaining to the sale and/or purchase of horses at the auction to be conducted by your organization on____/____/____. -

Louisiana Plantation Weddings in Fact, Fiction and Folklore
Louisiana State University LSU Digital Commons LSU Doctoral Dissertations Graduate School 2012 Wedding belles and enslaved brides: Louisiana plantation weddings in fact, fiction and folklore Cherry Lynne Levin Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_dissertations Part of the English Language and Literature Commons Recommended Citation Levin, Cherry Lynne, "Wedding belles and enslaved brides: Louisiana plantation weddings in fact, fiction and folklore" (2012). LSU Doctoral Dissertations. 3506. https://digitalcommons.lsu.edu/gradschool_dissertations/3506 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Doctoral Dissertations by an authorized graduate school editor of LSU Digital Commons. For more information, please [email protected]. WEDDING BELLES AND ENSLAVED BRIDES: LOUISIANA PLANTATION WEDDINGS IN FACT, FICTION AND FOLKLORE A Dissertation Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College In partial fulfillment of the Requirements for the degree of Doctor of Philosophy In The Department of English By Cherry Lynne Pyburn Levin B.A., University of Houston, 1975. M.A., University of California, Berkeley, 2000 M.A. Texas A&M University, 2004 May, 2012 Acknowledgments The following people have taught me much about literature and folklore as well as southern studies and I am deeply grateful for their willing donation of time and energy to see this project to completion. My Dissertation Director, John Wharton Lowe and Emeritus Professor Frank deCaro always took time to listen and give suggestions. -

Free Card Games to Download for Mac
1 / 3 Free Card Games To Download For Mac The 21 Game (Java Card Game Engine) v 1 0This project is crossplatform solution for creating almost all card games like 'Black Jack' or its Russian analog '21 '.. The goal of the game is to build stacks of cards (from king to ace), causing them to disappear off the screen.. Unlike other gaming environments, we had a peculiar vision: projecting the main board on our.. Free card games for Mac OS X (Belote, Bridge, Minibridge, Elevator Whist, President) to play against the computer with no need to register.. 1 0Spiderette Solitaire is similar to spider solitaire, but it plays with only a single deck of cards, instead of two. 1 0Get ready for a sting! Scorpion Solitaire is here! If you can beat this four suit scorpion solitaire variation, you are a true solitaire master! Scorpion Solitaire has great elements of spider solitaire with a few twists of its own!Crony Card Game Platform v.. Engine is written in Java Also card game 'Nine' is now OpenCG: An Open Card Game v.. Wiz Solitaire supports different deck formats allowing you to choose between Anywhere Board Games v.. Relax and have fun with classic games like solitaire, slingo, slots, bingo, dominos, and more! Mike's Cards is not free, but you can download its trial version that includes a limited number of games.. It's not nearly as bad as the afore mentioned, but it's definitely up there Yukon Solitaire Card Game v. card games card games, card games for two people, card games for adults, card games online, card games io, card games for kids, card games to play by yourself, card games to play, card games for 3 people, card games for couples, card games for 2 or, at 4 Suit Yukon Spider Solitaire Ready to play a spider solitaire card game that's more Freecell Freecell 2. -

Solitaire Kindle
SOLITAIRE PDF, EPUB, EBOOK ALICE OSEMAN | 400 pages | 01 Aug 2014 | HarperCollins Publishers | 9780007559220 | English | London, United Kingdom Solitaire PDF Book If your second card is a Two of Spades from the stockpile, you can then place that on top of the Ace of Spades in the Foundation pile. Patience Solitaire. Spider Solitaire. Converting to work mode. Easter Solitaire. Klondike Solitaire is the most popular card game around. Unlock an entire set to be able to use it in the game. This is called turn 3. Some players limit it to one pass. Double Solitaire Turn 1. Site Update. Game Sounds: Off On. Klondike Turn 1 Turn 3. It is now a global phenomenon. Card Game Klondike. We also created Solitaire Brain so you can learn some fun facts while you play. Read more in our Privacy Policy or manage your privacy settings. Back Game Won! Play the game of the day - Everyday, we introduce a new winnable game. All in A Row. Pyramid 2 Passes. Gold was discovered in the northwest region of Canada, or the Klondike area of the Yukon territory, which triggered a rush of miners from the west coast of the United States. All these variations are meant to create various degrees of difficulty, depending on how hard of a game you want to play. Play Now Addicted to FreeCell? Yellow Suits. Forty Thieves Solitaire. Solitaire Writer Tableau: This is the area where you have seven columns, with the first column containing one card and each sequential column containing one more additional card. Groups of turned up cards can be moved too on the tableau. -
Playing Cards
PLAYING CARDS The first session of this sale is comprised in large part of the playing card and ephemera collection of Bob and Rhonda Hawes, of Hamden, Conn. The couple met in 1976, married two years later, and have jointly pursued their shared love of cards and card games ever since. Their introduction to collecting came in the early 1980s through Robert Kissel, a bridge- playing friend and student at Yale studying old European card games. Robert taught them gameplay of Tarock and Skat, and in 1986 encouraged the Haweses to attend their first playing card conference, held in nearby New Haven by the International Playing Card Society. Reluctantly, the Haweses agreed to go. The rest, so they say, is history. At the IPCS conference the Haweses met Gene Hochman, an authority on early American playing cards and author of The Encyclopedia of American Playing Cards. Through conversations with him, they were inspired to form a private collection and dedicated themselves to ferreting out 1 top material along the flea market and antique show circuits. They collected widely in books, advertising, postcards, trade cards, stamps, bridge tallies, and more, but eventually narrowed their focus to more specialized areas, most notably non-standard artistic decks, and particularly transformation decks. After more than two decades of active collecting, and following retirement from their previous careers, the couple decided to auction the material as they prepare for the next phase in life, including travel, new hobbies, and volunteer work. Of course, this phase will go on to include attendance at several annual playing card conferences, regular get- togethers with the many friends they’ve made along the way – and lots of games of cards.