DOCSLIB.ORG

Modeling Rocket Flight in the Low-Friction Approximation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modeling Rocket Flight in the Low-Friction Approximation Undergraduate Journal of Mathematical Modeling: One + Two Volume 6 | 2014 Fall Article 5 2014 Modeling Rocket Flight in the Low-Friction Approximation Logan White University of South Florida Advisors: Manoug Manougian, Mathematics and Statistics Razvan Teodorescu, Physics Problem Suggested By: Razvan Teodorescu Follow this and additional works at: https://scholarcommons.usf.edu/ujmm Part of the Mathematics Commons UJMM is an open access journal, free to authors and readers, and relies on your support: Donate Now Recommended Citation White, Logan (2014) "Modeling Rocket Flight in the Low-Friction Approximation," Undergraduate Journal of Mathematical Modeling: One + Two: Vol. 6: Iss. 1, Article 5. DOI: http://dx.doi.org/10.5038/2326-3652.6.1.4861 Available at: https://scholarcommons.usf.edu/ujmm/vol6/iss1/5 Modeling Rocket Flight in the Low-Friction Approximation Abstract In a realistic model for rocket dynamics, in the presence of atmospheric drag and altitude-dependent gravity, the exact kinematic equation cannot be integrated in closed form; even when neglecting friction, the exact solution is a combination of elliptic functions of Jacobi type, which are not easy to use in a computational sense. This project provides a precise analysis of the various terms in the full equation (such as gravity, drag, and exhaust momentum), and the numerical ranges for which various approximations are accurate to within 1%. The analysis leads to optimal approximations expressed through elementary functions, which can be implemented for efficient flight prediction on simple computational devices, such as smartphone applications. Keywords Differential Equations, Rocket Flight, Motion This article is available in Undergraduate Journal of Mathematical Modeling: One + Two: https://scholarcommons.usf.edu/ujmm/vol6/iss1/5 White: Modeling Rocket Flight in the Low-Friction Approximation MODELING ROCKET FLIGHT IN THE LOW-FRICTION APPROXIMATION 3 PROBLEM STATEMENT & MOTIVATION The question under investigation in this paper is: How can we best model rocket flight with closed-form equations? MATHEMATICAL DESCRIPTION AND SOLUTION APPROACH I. EXACT SOLUTIONS Assuming that the relationship between the mass of the rocket 푚(푡) at time 푡 and the rate of mass depletion 푚′(푡) is proportional, gives 푑푚 = −푄 푚(푡) 푑푡 for some constant 푄. Hence the mass remaining at time 푡, found through separation of variables and subsequent integration, is −푄 푡 푚(푡) = 푚0 푒 where 푡 ≥ 0 (1) and 푚0 = 푚(0) is the initial mass of the rocket. By Newton’s Second Law, the sum of forces 퐹 on an object equals the product of the object’s mass and acceleration: 푛 푑푣 ∑ 퐹 = 푚 . (2) 푑푡 =1 The forces summed in the direction of the rocket’s flight following liftoff are the gravitational force: Produced by The Berkeley Electronic Press, 2014 Undergraduate Journal of Mathematical Modeling: One + Two, Vol. 6, Iss. 1 [2014], Art. 5 4 LOGAN WHITE 퐺 푚 푚(푡) 퐹 = − 푒 , (3) 푦2 where G is Newton’s gravitational constant, 푚푒 is Earth’s mass, and 푦 = 푦(푡) is the vertical position of the rocket relative to Earth’s center, and the force of thrust caused by the ejection of fuel out of the rocket’s nozzle: 푑푚 퐹 = −푐 , (4) 푡 푑푡 where 푐 is the constant exhaust speed, relative to the rocket. Letting 훼 = 퐺 푚푒 and 훽 = 푄 푐 and combining equations (2), (3), and (4), we receive a differential equation into which we can substitute equation (1) like so: 푑푣 훼 푚(푡) 푑푚 푑푣 훼 푚 푒−푄푡 푚(푡) = − − 푐 ⟹ (푚 푒−푄푡) = − 0 + 훽 (푚 푒−푄푡) . 푑푡 푦2 푑푡 0 푑푡 푦2 0 Simplifying, we receive 푑푣 훼 = 훽 − , (5) 푑푡 푦2 Noticing that 푣 = 푑푦/푑푡 : 푑푣 푑푣 푑푦 푑푣 = = 푣 . (6) 푑푡 푑푦 푑푡 푑푦 Substituting equation (6) into our second-order differential equation (5), we arrive at the equation: 푑푣 훼 훼 푣 = 훽 − ⟹ 푣 푑푣 = 훽 푑푦 − 푑푦 푑푦 푦2 푦2 and integrate: https://scholarcommons.usf.edu/ujmm/vol6/iss1/5 DOI: http://dx.doi.org/10.5038/2326-3652.6.1.4861 White: Modeling Rocket Flight in the Low-Friction Approximation MODELING ROCKET FLIGHT IN THE LOW-FRICTION APPROXIMATION 5 푣(푡) 푦(푡) 푦(푡) 훼 [ 푣(푡) ]2 훼 [ 푦(푡) − 푟 ] ∫ 푣 푑푣 = ∫ 훽 푑푦 − ∫ 푑푦 ⟹ = 훽 [ 푦(푡) − 푟 ] − 푒 , 푦2 2 푒 푟 푦(푡) 푣=0 푦=푟푒 푦=푟푒 푒 noting that the rocket begins its flight on the Earth’s surface, i.e., 푦(0) = 푟푒 where 푟푒 is the radius of the Earth. If we substitute 푣(푡) = 푑푦/푑푡, we arrive at 2 푑푦 훼 [푦 − 푟푒] ( ) = 2 훽 [푦 − 푟푒] − 2 . (7) 푑푡 푟푒 푦 Separating variables in equation (7) gives 푑푦 푑푡 = 훼 [푦 − 푟푒] √2 훽 [푦 − 푟푒] − 2 푟푒 푦 and integrating yields 푡 푦(푡) 푑푦 푧(푡) 푑푧 ∫ 푑 푡 = ∫ = ∫ , 푡=0 푦=푟푒 훼 푧=0 1 (8) √2[푦 − 푟푒] [훽 − ] − 푟푒푦 2훼 푟푒훽 푟푒 √ [푧] [ + 푧 ] 푟푒 훼 1 − (− ) 푟푒 and we get an equation that is difficult to use. This solution is not practical from a computational standpoint, as it involves two different types of Jacobi elliptic integrals. Instead, it would probably be more useful to investigate various methods of approximation by which we can simplify the function further. 1. APPROXIMATIONS AND ERROR 1 − 푟푒 The simplest approximation of equation (8) that we consider neglects the effect of the 푧(푡) 1−(− ) 푟푒 term. This approximation leads to a solution that is unsatisfactory because it ignores the effects of gravity: Produced by The Berkeley Electronic Press, 2014 Undergraduate Journal of Mathematical Modeling: One + Two, Vol. 6, Iss. 1 [2014], Art. 5 6 LOGAN WHITE 훽 푧(푡) = 푡2 . (9) 2 In order to arrive at a more satisfactory solution, we will have to look at geometric series. The 푎 sum of the infinite and convergent geometric series ∑∞ 푎 is 1 , where 푎 is the first term of =1 1−푟 1 the series and 푟 is the common ratio. The term in the denominator of the right side of equation (8) that makes the equation difficult to integrate is 1 − 푟 1 푧(푡) [푧(푡)]2 푒 = − + − + ⋯ . (10) −푧(푡) 푟 푟2 3 1 − ( ) 푒 푒 푟푒 푟푒 1 푧(푡) when expressed as the sum of an infinite geometric series with 푎1 = − and 푟 = − 푟푒 푟푒 The total sum (10) can be approximated by simply taking the first few terms of the series. All of this can be done only under the assumption that 푧(푡) ≪ 푟푒, which makes the series convergent. However, this is always going to be true for the first stage of any multi-stage rocket flight. The error of any order approximation is going to be less than 0.01 (=1%) as follows: 1 푧(푡) [푧(푡)]2 푆푛 = − + 2 − 3 + ⋯ + 푎푛 + ⋯ . 푟푒 푟푒 푟푒 푎푛 is neglected as having less than 1% of the total sum 푆푛. So 1 푧(푡) [푧(푡)]2 푆푛 = − + 2 − 3 + ⋯ + 푅푛, 푟푒 푟푒 푟푒 where 푅푛 is the remainder and error term used to represent the terms 푎푛 and beyond. In particular, https://scholarcommons.usf.edu/ujmm/vol6/iss1/5 DOI: http://dx.doi.org/10.5038/2326-3652.6.1.4861 White: Modeling Rocket Flight in the Low-Friction Approximation MODELING ROCKET FLIGHT IN THE LOW-FRICTION APPROXIMATION 7 푎 푅 = 푛 . 푛 푧(푡) 1 − (− ) 푟푒 Because 푎푛 < 0.01, it must be true that 푅푛 < 0.01, so all errors are less than 1%. i. ZERO-ORDER APPROXIMATION In the zero-order approximation, the first term is taken from the infinite series (10) and used to approximate the sum of the series. When this substitution is carried out and the integrand simplified, we obtain 푧(푡) 푑푧 1 푡 = ∫ = √2 푧(푡) (훽 − 푔) . 푧=0 √2푧(푡)(훽 − 푔) 2(훽 − 푔) Solving for 푧(푡), we get 푡2 푧(푡) = (훽 − 푔). (11) 2 푧(푡) If the zero-order approximation is only reasonable when ≤ 0.01, the time domain 0 ≤ 푡 ≤ 푇0 푟푒 can be found as follows: 훽 − 푔 0.02 푟 0.01 푟 = 푇2 ( ) ⇒ 푇 = √ 푒 . 푒 0 2 0 훽 − 푔 Equation (11) provides a quadratic approximation of the first stage of a rocket flight; however, it does not account for variation in gravitational force. Instead, it assumes a constant force 푚푔 that would only be present at Earth’s surface. Because we are assuming a varying gravitational force, it is necessary to use a first-order approximation. ii. FIRST-ORDER APPROXIMATION Produced by The Berkeley Electronic Press, 2014 Undergraduate Journal of Mathematical Modeling: One + Two, Vol. 6, Iss. 1 [2014], Art. 5 8 LOGAN WHITE Taking the first two terms of the series (10) and substituting in for the sum of the series, we arrive at 푡 푧(푡) 푑푧 푧(푡) 푑푧 ∫ 푑푡 = ∫ = ∫ 2 2 푡=0 푧=0 푧=0 √퐴 [(푧 + 휅) − 휅 ] (12) 2훼 푟푒 훽 1 푧 √ (푧) ( − + 2) 푟푒 훼 푟푒 푟푒 2 훽− where 퐴 = and 휅 = . Using the trigonometric substitution 푧 = 휅 sec 휃 − 휅 and 푑푧 = 푟푒 퐴 휅 sec 휃 tan 휃 푑휃, equation (12) evaluates to 푡 1 휅 sec 휃−휅 휅 sec 휃 tan 휃 ∫ 푑푡 = ∫ 푑휃 2 2 2 푡=0 √퐴 휃0 √휅 sec 휃 − 휅 휅 sec 휃−휅 = ∫ sec 휃 푑휃 휃0 푧(푡) 1 푧 + 휅 + √(푧 + 휅)2 − 휅2 = ln | | . √퐴 휅 푧=0 Evaluated at its upper and lower limits, this equation gives us our position function of time, 푧(푡), which is a hyperbolic cosine function: 푧(푡) = 휅 cosh(푡√퐴) − 휅 .
Load more

Recommended publications
  • Coplanar Air Launch with Gravity-Turn Launch Trajectories
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by AFTI Scholar (Air Force Institute of Technology) Air Force Institute of Technology AFIT Scholar Theses and Dissertations Student Graduate Works 3-23-2004 Coplanar Air Launch with Gravity-Turn Launch Trajectories David W. Callaway Follow this and additional works at: https://scholar.afit.edu/etd Part of the Aerospace Engineering Commons Recommended Citation Callaway, David W., "Coplanar Air Launch with Gravity-Turn Launch Trajectories" (2004). Theses and Dissertations. 3922. https://scholar.afit.edu/etd/3922 This Thesis is brought to you for free and open access by the Student Graduate Works at AFIT Scholar. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of AFIT Scholar. For more information, please contact [email protected]. COPLANAR AIR LAUNCH WITH GRAVITY-TURN LAUNCH TRAJECTORIES THESIS David W. Callaway, 1st Lieutenant, USAF AFIT/GAE/ENY/04-M04 DEPARTMENT OF THE AIR FORCE AIR UNIVERSITY AIR FORCE INSTITUTE OF TECHNOLOGY Wright-Patterson Air Force Base, Ohio APPROVED FOR PUBLIC RELEASE; DISTRIBUTION UNLIMITED. The views expressed in this thesis are those of the author and do not reflect the official policy or position of the United States Air Force, Department of Defense, or the United States Government. AFIT/GAE/ENY/04-M04 COPLANAR AIR LAUNCH WITH GRAVITY-TURN LAUNCH TRAJECTORIES THESIS Presented to the Faculty Department of Aeronautics and Astronautics Graduate School of Engineering and Management Air Force Institute of Technology Air University Air Education and Training Command In Partial Fulfillment of the Requirements for the Degree of Master of Science in Aeronautical Engineeering David W.
    [Show full text]
  • A Tool for Preliminary Design of Rockets Aerospace Engineering
    A Tool for Preliminary Design of Rockets Diogo Marques Gaspar Thesis to obtain the Master of Science Degree in Aerospace Engineering Supervisor : Professor Paulo Jorge Soares Gil Examination Committee Chairperson: Professor Fernando José Parracho Lau Supervisor: Professor Paulo Jorge Soares Gil Members of the Committee: Professor João Manuel Gonçalves de Sousa Oliveira July 2014 ii Dedicated to my Mother iii iv Acknowledgments To my supervisor Professor Paulo Gil for the opportunity to work on this interesting subject and for all his support and patience. To my family, in particular to my parents and brothers for all the support and affection since ever. To my friends: from IST for all the companionship in all this years and from Coimbra for the fellowship since I remember. To my teammates for all the victories and good moments. v vi Resumo A unica´ forma que a humanidade ate´ agora conseguiu encontrar para explorar o espac¸o e´ atraves´ do uso de rockets, vulgarmente conhecidos como foguetoes,˜ responsaveis´ por transportar cargas da Terra para o Espac¸o. O principal objectivo no design de rockets e´ diminuir o peso na descolagem e maximizar o payload ratio i.e. aumentar a capacidade de carga util´ ao seu alcance. A latitude e o local de lanc¸amento, a orbita´ desejada, as caracter´ısticas de propulsao˜ e estruturais sao˜ constrangimentos ao projecto do foguetao.˜ As trajectorias´ dos foguetoes˜ estao˜ permanentemente a ser optimizadas, devido a necessidade de aumento da carga util´ transportada e reduc¸ao˜ do combust´ıvel consumido. E´ um processo utilizado nas fases iniciais do design de uma missao,˜ que afecta partes cruciais do planeamento, desde a concepc¸ao˜ do ve´ıculo ate´ aos seus objectivos globais.
    [Show full text]
  • Hybrid Rocket Engine Design Optimization at Politecnico Di Torino: a Review
    aerospace Review Hybrid Rocket Engine Design Optimization at Politecnico di Torino: A Review Lorenzo Casalino † , Filippo Masseni † and Dario Pastrone *,† Politecnico di Torino, Dipartimento di Ingegneria Meccanica e Aerospaziale, Corso Duca degli Abruzzi 24, 10129 Torino, Italy; [email protected] (L.C.); fi[email protected] (F.M.) * Correspondence: [email protected] † These authors contributed equally to this work. Abstract: Optimization of Hybrid Rocket Engines at Politecnico di Torino began in the 1990s. A comprehensive review of the related research activities carried out in the last three decades is here presented. After a brief introduction that retraces driving motivations and the most significant steps of the research path, the more relevant aspects of analysis, modeling and achieved results are illustrated. First, criteria for the propulsion system preliminary design choices (namely the propellant combination, the feed system and the grain design) are summarized and the engine modeling is presented. Then, the authors describe the in-house tools that have been developed and used for coupled trajectory and propulsion system design optimization. Both deterministic and robust-based approaches are presented. The applications that the authors analyzed over the years, starting from simpler hybrid powered sounding rocket to more complex multi-stage launchers, are then presented. Finally, authors’ conclusive remarks on the work done and their future perspective in the context of the optimization of hybrid rocket propulsion systems are reported. Citation: Casalino, L.; Masseni, F.; Pastrone, D. Hybrid Rocket Engine Keywords: Hybrid Rocket Engines; multidisciplinary optimization; robust optimization Design Optimization at Politecnico di Torino: A Review. Aerospace 2021, 8, 226.
    [Show full text]
  • Orbital Rendezvous Using an Augmented Lambert Guidance Scheme By
    Orbital Rendezvous Using an Augmented Lambert Guidance Scheme by Sara Jean MacLellan B.S. Aerospace Engineering Embry-Riddle Aeronautical University, 2003 SUBMITTED TO THE DEPARTMENT OF AERONAUTICS AND ASTRONAUTICS IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN AERONAUTICS AND ASTRONAUTICS AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY JUNE 2005 @ 2005 Sara Jean MacLellan. All rights reserved. The author hereby grants to MIT permission to reproduce and distribute publicly paper and electronic copies of this thesis document in whole or in part. Signature of Author: Department of Aeronautics and Astronautics May 06, 2005 Certified by: V Andrew Staugler Senior Member of the Technical Staff The Charles Stark Draper Laboratory, Inc. Technical Advisor Accepted by: Richard H. Battin, Ph.D. Senior Lecturer of Aeronautics and Astronautics Thesis Supervisor Accepted bv Jaime Peraire, Ph.D. MASSACHUSS INS E Professor of Aeronautics and Astronautics OF TECHNOLOGY Chair, Committee on Graduate Students DEC 1E2005 LIBRARIES AERO I [This page intentionally left blank.] 40600 Orbital Rendezvous Using an Augmented Lambert Guidance Scheme by Sara Jean MacLellan Submitted to the Department of Aeronautics and Astronautics on May 06, 2005, in partial fulfillment of the requirements for the degree of Master of Science in Aeronautics and Astronautics Abstract The development of an Augmented Lambert Guidance Algorithm that matches the po- sition and velocity of an orbiting target spacecraft is presented in this thesis. The Aug- mented Lambert Guidance Algorithm manipulates the inputs given to a preexisting Lam- bert guidance algorithm to control the boost of a launch vehicle, or chaser, from the surface of the Earth to a transfer trajectory enroute to the aim point.
    [Show full text]
  • On Four New Methods of Analytical Calculation of Rocket Trajectories
    aerospace Article On Four New Methods of Analytical Calculation of Rocket Trajectories Luís M. B. C. Campos *,† and Paulo J. S. Gil † CCTAE, IDMEC, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, 1049-001 Lisboa, Portugal; [email protected] * Correspondence: [email protected]; Tel.: +351-21-841-72-67 † These authors contributed equally to this work. Received: 15 June 2018 ; Accepted: 27 July 2018; Published: 15 August 2018 Abstract: The calculation of rocket trajectories is most often performed using purely numerical methods that account for all relevant parameters and provide the required results. There is a complementary need for analytical methods that make more explicit the effect of the various rocket and atmospheric parameters of the trajectory and can be used as test cases with unlimited accuracy. The available analytical methods take into account (i) variable rocket mass due to propellant consumption. The present paper includes four new analytical methods taking into account besides (i) also (ii) nonlinear aerodynamic forces proportional to the square of the velocity and (iii) exponential dependence of the mass density with altitude for an isothermal atmospheric layer. The four new methods can be used in “hybrid analytical-numerical” approach in which: (i) the atmosphere is divided into isothermal rather than homogeneous layers for greater physical fidelity; and (ii) in each layer, an exact analytical solution of the equations of motion with greater mathematical accuracy than a numerical approximation is used. This should allow a more accurate calculation of rocket trajectories while discretizing the atmosphere into a smaller number of layers.
    [Show full text]
  • Rapid Trajectory Optimization for the ARES I Launch Vehicle
    Rapid Trajectory Optimization For the ARES I Launch Vehicle Greg A. Dukeman∗ NASA Marshall Space Flight Center, Huntsville, Alabama, 35812, USA Ashley D. Hilly Dynamic Concepts Incorporated, Huntsville, Alabama, 35812, USA A simplified ascent trajectory optimization procedure has been developed with appli- cation to NASA's proposed Ares I launch vehicle. In the interest of minimizing bending loads and ensuring safe separation of the first-stage solid rocket motor, the vehicle is con- strained to follow a gravity-turn trajectory. This reduces the design space to just two free parameters, the pitch rate after a short vertical rise phase to clear the launch pad, and initial launch azimuth. The pitch rate primarily controls the in-plane parameters (altitude, speed, flight path angle) of the trajectory whereas the launch azimuth primarily controls the out-of-plane portion (velocity heading.) Thus, the optimization can be mechanized as two one-dimensional searches that converge quickly and reliably. The method is compared with POST-optimized trajectories to verify its optimality. Nomenclature DOLILU Day-Of-Launch I-Load Update ISS International Space Station KSC Kennedy Space Center MAV ERIC Marshall Aerospace Vehicle Representation in C MECO Main Engine Cutoff OT IS Optimal Trajectories by Implicit Simulation P OST Program to Optimize Simulated Trajectories SRB Solid Rocket Booster i orbital inclination φ geocentric latitude launch azimuth, positive clockwise from local North I. Introduction An important ingredient of launch vehicle design and analysis and, ultimately, launch operations, is the capability to optimize ascent trajectories while satisfying constraints such as bending moments. These constraints are significantly influenced by wind conditions that exist in the region of maximum dynamic pressure.
    [Show full text]
  • Project Argo
    Project Argo A Proposal for a Mars Sample Return System J. Cunningham, S. Thompson, C. Ayon, W. Gallagher, E. Gomez, A. Kechejian, A. Miller Pyxis Aerospace, Cal Poly Pomona, Pomona, CA, 91768, USA AIAA Undergraduate Team Space Transportation Design Competition, 2016 Abstract Pyxis Aerospace at Cal Poly Pomona is pleased to present Project Argo, its proposal for a Mars Sample Return System as requested by the American Institute of Aeronautics and Astronautics. The goal of Project Argo is to travel to Mars, retrieve a sample collected by a rover on the Martian surface, and return it to Earth. To accomplish this goal, we have designed three vehicles: the Earth Return Vehicle (ERV), the Mars Ascent Vehicle (MAV), and the Mars Landing Platform (MLP). The three vehicles will launch on July 24, 2020 and travel together as one unit. The MAV and the MLP will be enclosed in a backshell/heat shield similar to previous Mars missions, and the ERV will act as the cruise stage. The vehicles will arrive at Mars Feb 17, 2021. After Mars orbit capture, the MAV/MLP will separate and enter the Martian atmosphere. The MLP, carrying the MAV, will make a precision landing within 5 km of the rover location. After the sample cache has been received and secured, the MAV will launch from the Martian surface and rendezvous with the ERV, which will have been left in a parking orbit. The sample cache will be transferred to the ERV, and the ERV will return to Earth, arriving in May 2025. The ERV will capture into Earth orbit using a combination of propulsive maneuvers and aerobraking to bring it to a suitable orbit, and rendezvous with the ISS.
    [Show full text]
  • Proceedings, ITC/USA
    Rocket Trajectory Analysis from Telemetered Acceleration and Attitude Data Item Type text; Proceedings Authors Cooper, Oscar L. Publisher International Foundation for Telemetering Journal International Telemetering Conference Proceedings Rights Copyright © International Foundation for Telemetering Download date 24/09/2021 08:20:54 Link to Item http://hdl.handle.net/10150/578492 ROCKET TRAJECTORY ANALYSIS FROM TELEMETERED ACCELERATION AND ATTITUDE DATA1 DR. OSCAR L. COOPER Research Foundation Oklahoma State University Stillwater, Oklahoma Summary Double integration of the longitudinal acceleration of a sounding rocket is useful as a simple means of determining its trajectory. Reasonably accurate altitude calculations can be made by this method except when surface winds alter the launch angle of the rocket. Surface wind velocity corrections can be introduced to correct velocity and position information in the horizontal direction, but accurate wind correction data is difficult to obtain for all rockets. A special solar aspect sensor was designed to be used with a commercially available magnetic aspect sensor for rocket attitude determination. This attitude data allows the longitudinal acceleration to be broken more accurately into three vector components. A feasibility study of the aspect system was made using three Aerobee-150 rockets. A digital computer trajectory program was written to utilize aspect and acceleration data for trajectory analysis. It is evident that rocket attitude data is a useful supplement to the longitudinal acceleration data for trajectory determination. More accurate magnetic aspect data is necessary, however, to refine the longitudinal acceleration technique. Introduction During the past several years an unusually large amount of upper atmospheric research has been done by means of sounding rockets, long range probes and earth satellites.
    [Show full text]
  • 4. Spacecraft Guidance MAE 342 2016
    2/12/20 Spacecraft Guidance Space System Design, MAE 342, Princeton University Robert Stengel • Oberth’s “Synergy Curve” • Explicit ascent guidance • Impulsive ΔV maneuvers • Hohmann transfer between circular orbits • Sphere of gravitational influence • Synodic periods and launch windows • Hyperbolic orbits and escape trajectories • Battin’s universal formulas • Lambert’s time-of-flight theorem (hyperbolic orbit) • Fly-by (swingby) trajectories for gravity assist Copyright 2016 by Robert Stengel. All rights reserved. For educational use only. 1 http://www.princeton.edu/~stengel/MAE342.html 1 Guidance, Navigation, and Control • Navigation: Where are we? • Guidance: How do we get to our destination? • Control: What do we tell our vehicle to do? 2 2 1 2/12/20 Energy Gained from Propellant Specific energy = energy per unit weight Hermann Oberth V 2 E = h + 2g h :height; V :velocity Rate of change of specific energy per unit of expended propellant mass d dh V dV 1 ⎛ dh V dV ⎞ E = + = + dm dm g dm (dm dt) ⎝⎜ dt g dt ⎠⎟ 1 ⎛ dh 1 dv ⎞ 1 ⎛ 1 ⎞ = + vT = V sinγ + vT (T − mg) (dm dt) ⎝⎜ dt g dt ⎠⎟ (dm dt) ⎝⎜ g ⎠⎟ 1 ⎛ VT ⎞ = V sinγ + cosα −V sinγ (dm dt) ⎝⎜ mg ⎠⎟ 3 3 Oberth’s Synergy Curve γ : Flight Path Angle θ: Pitch Angle α: Angle of Attack dE/dm maximized when α = 0, or θ = γ, i.e., thrust along the velocity vector Approximate round-earth equations of motion dV T Drag = cosα − − gsinγ dt m m dγ T ⎛ V g ⎞ = sinα + ⎜ − ⎟ cosγ dt mV ⎝ r V ⎠ 4 4 2 2/12/20 Gravity-Turn Pitch Program With angle of attack, α = 0 dγ dθ ⎛ V g ⎞ = = − cosγ dt dt ⎝⎜ r V
    [Show full text]
  • Entry, Descent, Landing and Ascent
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems V Edition 2009 - 10 Entry, Descent, Landing and Ascent Lecture notes - Ver. 1.0.3 Author: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Equations of motion for trajectory analysis 1 1.1 Introduction and nomenclature . 1 1.2 Reference Frames . 2 1.3 Equations of motion . 3 1.3.1 Kinematic equations . 3 1.3.2 Dynamic equations . 3 1.3.3 Forces . 4 1.3.4 Equations of motion for flight over a spherical rotating Earth . 6 1.4 Particular cases . 7 1.4.1 Free–flight (T = 0; m = const) . 7 1.4.2 Launch and entry in the equatorial plane (' = 0) . 7 1.4.3 Order of magnitude of different terms in the E.o.M. 8 1.4.4 Motion over a spherical, non{rotating Earth (! = 0) . 8 1.4.5 Motion over a flat, non{rotating planet . 9 1.5 The problem of attitude . 9 2 Atmospheric entry 11 2.1 Assumptions and formulation of the equations of motion . 11 2.2 The atmosphere . 12 2.3 Equation of motion in nondimensional form . 13 2.4 Phases of atmospheric entry . 17 2.5 Gliding Entry . 18 2.6 Ballistic entry . 21 2.7 Thermal control . 23 2.7.1 Gliding entry . 24 2.7.2 Ballistic entry . 25 2.8 Critical analysis of gliding and ballistic entry . 27 2.8.1 Gliding vs ballistic entry: historical facts . 27 2.8.2 Gliding vs ballistic entry: a comparison .
    [Show full text]
  • Lecture 7 Launch Trajectories
    AA 284a Advanced Rocket Propulsion Lecture 7 Launch Trajectories Prepared by Arif Karabeyoglu Department of Aeronautics and Astronautics Stanford University and Mechanical Engineering KOC University Fall 2019 Stanford University AA284a Advanced Rocket Propulsion Orbital Mechanics - Review • Newton’s law of gravitation: mMG Fg = r2 – M, m: Mass of the bodies – r: Distance between the center of masses of the two bodies – Fg: Gravitational attraction force between the two bodies – G: Universal gravitational constant • Assume that m is the mass of the spacecraft and M is the mass of the celestial body. Arrange the force expression as (Note that m << M) m 2 Fg = = g m = M G g = r r2 • Here the gravitational parameter has been introduced for convenience. It is a constant for a given celestial mass. For Earth 3 2 = 398,600 km /sec • For circular orbit: centrifugal force balancing the gravitational force acting on the satellite – Orbital Velocity: V = co r r3 – Orbital Period: P = 2 Stanford University 2 Karabeyoglu AA284a Advanced Rocket Propulsion Orbital Mechanics - Review • Fundamental Assumptions: – Two body assumption • Motion of the spacecraft is only affected my a single central body – The mass of the spacecraft is negligible compared to the mass of the celestial body – The bodies are spherically symmetric with the masses concentrated at the center of the sphere – No forces other than gravity (and inertial forces) r r = k r3 • Solution: • Sections of a cone Stanford University 3 Karabeyoglu AA284a Advanced Rocket Propulsion Orbital Mechanics - Review • Solution: – Orbits of any conic section, elliptic, parabolic, hyperbolic – Energy is conserved in the conservative force field.
    [Show full text]
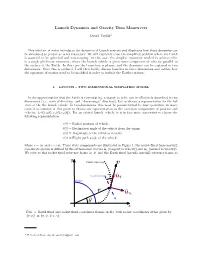
  • Launch Dynamics and Gravity Turn Maneuvers
    Launch Dynamics and Gravity Turn Maneuvers David Yaylalia This brief set of notes introduces the dynamics of launch systems and illustrates how these dynamics can be simulated to predict a rocket trajectory. We will explicitly treat the simplified problem where the Earth is assumed to be spherical and non-rotating. In this case, the simplest maneuver needed to achieve orbit is a single pitch-over maneuver, where the launch vehicle is given some component of velocity parallel to the surface of the Earth. In this case the trajectory is planar, and the dynamics can be captured in two dimensions. Once this is outlined, I will then briefly discuss launches in three dimensions and outline how the equations of motion need to be modified in order to include the Earths rotation. I. LAUNCH { TWO DIMENSIONAL SIMPLIFIED MODEL In the approximation that the Earth is non-rotating, a launch to orbit can be effectively described in two dimensions (i.e., vertical direction, and \down-range" direction). Let us choose a representation for the full state of the the launch vehicle. In two-dimensions, this must be parameterized by four quantities; in many cases it is common at this point to choose our representation as the cartesian components of position and velocity, fx(t); y(t); vx(t); vy(t)g. For an orbital launch vehicle, it is in fact more convenient to choose the following representation: r(t) ≡ Radial position of vehicle θ(t) ≡ Declination angle of the vehicle from the origin v(t) ≡ Magnitude of the vehicle's velocity γ(t) ≡ Flight path angle of the vehicle; where r = jrj and v = jvj.
    [Show full text]