DOCSLIB.ORG

How Yield Strength and Fracture Toughness Considerations Can Influence Fatigue Design Procedures for Structural Steels

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
How Yield Strength and Fracture Toughness Considerations Can Influence Fatigue Design Procedures for Structural Steels How Yield Strength and Fracture Toughness Considerations Can Influence Fatigue Design Procedures for Structural Steels The K,c /cfys ratio provides significant information relevant to fatigue design procedures, and use of NRL Ratio Analysis Diagrams permits determinations based on two relatively simple engineering tests BY T. W. CROOKER AND E. A. LANGE ABSTRACT. The failure of welded fatigue failures in welded structures probable mode of failure, the impor­ structures by fatigue can be viewed are primarily caused by crack propa­ tant factors affecting both fatigue and as a crack growth process operating gation. Numerous laboratory studies fracture, and fatigue design between fixed boundary conditions. The and service failure analyses have re­ procedures are discussed for each lower boundary condition assumes a peatedly shown that fatigue cracks group. rapidly initiated or pre-existing flaw, were initiated very early in the life of and the upper boundary condition the structure or propagated to failure is terminal failure. This paper outlines 1-6 Basic Aspects the modes of failure and methods of from pre-existing flaws. Recognition of this problem has The influence of yield strength and analysis for fatigue design for structural fracture toughness on the fatigue fail­ steels ranging in yield strength from 30 lead to the development of analytical to 300 ksi. It is shown that fatigue crack techniques for fatigue crack propaga­ ure process is largely a manifestation propagation characteristics of steels sel­ tion and the gathering of a sizeable of the role of plasticity in influencing dom vary significantly in response to amount of crack propagation data on the behavior of sharp cracks in struc­ broad changes in yield strength and frac­ a wide variety of structural materials. tural metals. The degree of plasticity ture toughness. However, strength and However, a degree of organization involved in a given situation influences toughness do vary widely among struc­ and perspective has been lacking in both the mechanical behavior of tural steels, and thereby exert profound much of this work. Preoccupation by cracks and the methods of analysis effects on the fatigue failure process. By which can be applied to the problem. applying the principles of the NRL Ratio researchers with crack propagation Analysis Diagram, an analysis is pre­ laws has obscured the fact that crack The degree of plasticity associated propagation is only a portion of the with a crack can be categorized into sented whereby the plane strain fracture 7 toughness to yield strength ratio (Ku/ fatigue failure process. Furthermore, one of three situations. First, there as.) can be employed to determine fa­ it is probably the portion of the fa­ can be gross ductile yielding where the tigue design procedures. The full spec­ tigue failure process least amenable to fully plastic state extends beyond the trum of structural steels is divided into a substantial improvement. vicinity of the crack and dominates three groups on the basis of fracture be­ The failure of welded structures by the behavior of the entire cracked havior: fatigue can be viewed as a crack body. Second, there can be large scale 1. Ductile plastic fracture mode (K,„/ growth process operating between localized yielding where the nominal a,. > 1.5). fixed boundary conditions—Fig. 1. deformations away from the vicinity 2. Elastic-plastic fracture mode (1.5 The lower boundary condition as­ of the crack are elastic. However, a > K,Joys > 0.5). sumes the existence of a rapidly initi­ plastic zone exists at the crack tip 3. Brittle elastic instability fracture ated or pre-existing flaw, and the up­ which, although contained in an elas­ mode C&0/<r»« < 0.5). per boundary condition is terminal tic field, is large in relation to the The probable mode of failure, the im­ failure. The initial conditions primari­ length of the crack and dimensions portant factors affecting both fatigue and ly rely on fabrication procedures, (usually thickness) of the cracked fracture, and fatigue design procedures body. Finally, there can be small scale are discussed for each group. quality control, nondestructive testing, or proof testing. Crack propagation localized yielding where the crack tip Introduction and terminal failure are design and plastic zone is small in relation to the crack size and thickness of the body. It is now generally recognized that material problems, and fatigue design procedures must take into account Figure 2 schematically illustrates both crack propagation and terminal T. W. CROOKER and E. A. LANGE are some of the mechanics of localized with the Strength of Metals Branch, failure. yielding, where the crack tip plastic Metallurgy Division, Naval Research Lab­ This paper provides guidelines for zone is enclosed in an elastic stress oratory, Washington, D. C. the use of thick-section steels in fa­ field. Under these conditions the size Paper based on presentations made at the tigue-loaded structures. Steels ranging of the plastic zone (2r ), i.e., the Conference on Fatigue of Welded Struc­ y tures in Brighton, England, July 6-9, 1970. in yield strength from 30 to 3000 ksi distance it extends directly in front of and the ASME Pressure Vessels and Pip­ are divided into three groups on the the crack tip, is considered to be a ing Division Conference in Denver, Colo., Sept. 16-17, 1970. basis of their fracture behavior. The function of the stress-intensity factor 488-s I OCTOBER 1970 (K), the yield strength of the material increases and the crack tip plastic curve is limited by upper and lower (o-g,s), the stress state at the crack tip zone becomes large in relation to inflection points. The lower inflection (plane stress or plane strain), and the physical dimensions, successive cor­ point is indicative of nonpropagating mode of load application (monotonic rections must be applied and empiri­ fatigue cracks and occurs under ex­ or cyclic) :7 cism creeps into the fracture mechan­ ceedingly low stress intensities, where ics analysis. Nevertheless, the remain­ the crack growth rates are of the 2r = — (X/V )'--plane stress (1) der of this paper is presented using magnitude of the atomic spacing in y ys fracture mechanics terminology be­ the crystal lattice (~ 10~7 to 10-8 cause, despite analytical limitations, it in./cycle). The upper inflection point 2ry = — CKV/o-j^pIane strain (2) provides a common language basis. is caused by the onset of rapid un­ stable crack extension prior to termi­ Fatigue Crack Propagation nal fracture and places a critical limit 2ry = - (A^KJMatigue (3) on the fatigue resistance of structural HIT Crack Propagation Laws and Mechanisms metals. In actuality these equations merely With the recognition that crack The application of fracture provide rough estimates of the scale propagation is more critical than mechanics to fatigue set the trend for of yielding, mainly for the purposes of crack initiation for analyzing fatigue nearly all subsequent fatigue crack calculating an "effective" crack failure in many structures, numerous propagation studies. It is a successful length, based upon the actual crack efforts to develop engineering ap­ approach to crack propagation to the length plus a plastic zone size correc­ proaches to the problem were under­ extent that the stress-intensity factor taken. Much of this work was aimed tion (ry) for fracture mechanics describes the crack tip plasticity. Fa­ analyses.8 at revealing crack propagation laws tigue crack propagation occurs which would remain valid over a through cyclic plastic deformation oc­ Mechanically, large degrees of plas­ sufficiently broad range of experimen­ curring at the crack tip, regardless of ticity tend to inhibit fracture. High tal conditions. In their critical review how far plastic deformations exist be­ fracture toughness is associated with of crack propagation laws, Paris and yond the crack tip region.12'13 The the ability to develop large plastic 9 Erdogan showed that seemingly con­ relationship between gross cyclic plas­ zones or fully plastic yielding before tradictory results could be normalized tic strain and fatigue failure was rec­ fracture. However, fatigue crack prop­ to fit a single power-law curve by ognized a number of years ago and is agation properties do not seem to be relating the fatigue crack growth rate treated in detail by Manson.14 It was as sensitive to such distinctions, which (da/dN) to the stress-intensity factor used as the basis for a hypothesis for will be discussed in a later section. range (AK). The resulting equation fatigue crack propagation by Weiss.15 Analytically, the degree of accuracy was of the power-law form shown in More recently, Lehr and Liu16 have available for treating the mechanics of equation (4): shown that fatigue crack propagation sharp cracks in structural metals de­ m 7 8 da/dN = C(AK) (4) is caused by damage accumulation creases with increasing plasticity. ' due to strain cycling at the crack tip Fatigue and fracture under fully plas­ where C is a material constant and m and that the crack growth rate can be tic loading must be approached large­ is the slope of the power-law curve. 10 u calculated using strain cycling proper­ ly on an empirical basis. Linear-elastic More recent research ' has shown ties. fracture mechanics can be applied that the entire fatigue crack growth Consequently, both the proposed where the plastic zone resides within rate curve for most materials is actu­ mechanisms for fatigue crack propa­ an elastic stress field. However, rigor­ ally of sigmoidal form when plotted gation and the crack propagation laws ous analyses are limited to small scale on log-log coordinates, as shown in which seek to describe the phenom­ yielding. As the degree of yielding Fig. 3. The power-law portion of the enon in engineering terms are based upon cyclic crack tip plasticity.
Load more

Recommended publications
  • 10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
    EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch.
    [Show full text]
  • Fracture Toughness of FCC High Entropy Alloy
    Seoul National University High Entropy Alloy Traditional alloy High entropy alloy Minor Major element 3 element … Minor Major element 2 element 3 Major Major element element 1 Major Minor element 2 element 1 = ( ) 풏풏풏풏풏풏 풐풐 풏풆풆풆 ↑ ↔. 풄�풄풄풄풆풄풐풏풄풆 풆풆풆 ↑ ∆푆푐푐푐푐푐푐 푅푅푅 푅 Y.Zhang et al., Prog.Mat.Sci. 61, 1 (2014) (1) Thermodynamic : high entropy (3) Kinetics : sluggish diffusion (2) Structure : severe lattice distortion (4) Property : cocktail effect High entropy alloy : Potential candidate material for extreme environment applications Seoul National University Mechanical properties of HEA . Ashby map Bernd Gludovatz / SCIENCE VOL 345 ISSUE 6201 There are clearly stronger materials, which is understandable given that CrMnFeCoNi is a single-phase material, but the toughness of this high-entropy alloy exceeds that of virtually all pure metals and metallic alloys. Seoul National University Fracture toughness of HEA Bernd Gludovatz / SCIENCE VOL 345 ISSUE 6201 Although the toughness of the other materials decreases with decreasing temperature, the toughness of the high- entropy alloy remains unchanged. mechanical properties actually improve at cryogenic temperatures Seoul National University Fracture Toughness Testing Compact tension test & Three point bending test Pre-cracking Limitation Destructive Fracturing Complex testing procedure Cannot apply to in-service Development of testing method to measure the fracture properties more easily and more economically Seoul National University Indentation Fracture Toughness . Instrumented Indentation Technique (IIT) In-situ & In-field System, Non-destructive & Local test, Simple & fast . Indentation Cracking Method (cracking in indentation) 1 E 2 P = α K IC 3 H c 2 Only for ceramic materials (very brittle) [Vickers indenter, Macroscale] Seoul National University Indentation Fracture Toughness .
    [Show full text]
  • The Effect of Yield Strength on Inelastic Buckling of Reinforcing
    Mechanics and Mechanical Engineering Vol. 14, No. 2 (2010) 247{255 ⃝c Technical University of Lodz The Effect of Yield Strength on Inelastic Buckling of Reinforcing Bars Jacek Korentz Institute of Civil Engineering University of Zielona G´ora Licealna 9, 65{417 Zielona G´ora, Poland Received (13 June 2010) Revised (15 July 2010) Accepted (25 July 2010) The paper presents the results of numerical analyses of inelastic buckling of reinforcing bars of various geometrical parameters, made of steel of various values of yield strength. The results of the calculations demonstrate that the yield strength of the steel the bars are made of influences considerably the equilibrium path of the compressed bars within the range of postyielding deformations Comparative diagrams of structural behaviour (loading paths) of thin{walled sec- tions under investigation for different strain rates are presented. Some conclusions and remarks concerning the strain rate influence are derived. Keywords: Reinforcing bars, inelastic buckling, yield strength, tensil strength 1. Introduction The impact of some exceptional loads, e.g. seismic loads, on a structure may re- sult in the occurrence of post{critical states. Therefore the National Standards regulations for designing reinforced structures on seismically active areas e.g. EC8 [15] require the ductility of a structure to be examined on a cross{sectional level, and additionally, the structures should demonstrate a suitable level of global duc- tility. The results of the examinations of members of reinforced concrete structures show that inelastic buckling of longitudinal reinforcement bars occurs in the state of post{critical deformations, [1, 2, 4, 7], and in some cases it occurs yet within the range of elastic deformations [8].
    [Show full text]
  • High-Entropy Alloys
    REVIEWS High- entropy alloys Easo P. George 1,2*, Dierk Raabe3 and Robert O. Ritchie 4,5 Abstract | Alloying has long been used to confer desirable properties to materials. Typically , it involves the addition of relatively small amounts of secondary elements to a primary element. For the past decade and a half, however, a new alloying strategy that involves the combination of multiple principal elements in high concentrations to create new materials called high-entropy alloys has been in vogue. The multi-dimensional compositional space that can be tackled with this approach is practically limitless, and only tiny regions have been investigated so far. Nevertheless, a few high-entropy alloys have already been shown to possess exceptional properties, exceeding those of conventional alloys, and other outstanding high-entropy alloys are likely to be discovered in the future. Here, we review recent progress in understanding the salient features of high-entropy alloys. Model alloys whose behaviour has been carefully investigated are highlighted and their fundamental properties and underlying elementary mechanisms discussed. We also address the vast compositional space that remains to be explored and outline fruitful ways to identify regions within this space where high-entropy alloys with potentially interesting properties may be lurking. Since the Bronze Age, humans have been altering the out that conventional alloys tend to cluster around the properties of materials by adding alloying elements. For corners or edges of phase diagrams, where the number example, a few percent by weight of copper was added to of possible element combinations is limited, and that silver to produce sterling silver for coinage a thousand vastly more numerous combinations are available near years ago, because pure silver was too soft.
    [Show full text]
  • Lecture 42: Failure Analysis – Buckling of Columns Joshua Pribe Fall 2019 Lecture Book: Ch
    ME 323 – Mechanics of Materials Lecture 42: Failure analysis – Buckling of columns Joshua Pribe Fall 2019 Lecture Book: Ch. 18 Stability and equilibrium What happens if we are in a state of unstable equilibrium? Stable Neutral Unstable 2 Buckling experiment There is a critical stress at which buckling occurs depending on the material and the geometry How do the material properties and geometric parameters influence the buckling stress? 3 Euler buckling equation Consider static equilibrium of the buckled pinned-pinned column 4 Euler buckling equation We have a differential equation for the deflection with BCs at the pins: d 2v EI+= Pv( x ) 0 v(0)== 0and v ( L ) 0 dx2 The solution is: P P A = 0 v(s x) = Aco x+ Bsin x with EI EI PP Bsin L= 0 L = n , n = 1, 2, 3, ... EI EI 5 Effect of boundary conditions Critical load and critical stress for buckling: EI EA P = 22= cr L2 2 e (Legr ) 2 E cr = 2 (Lreg) I r = Pinned- Pinned- Fixed- where g Fixed- A pinned fixed fixed is the “radius of gyration” free LLe = LLe = 0.7 LLe = 0.5 LLe = 2 6 Modifications to Euler buckling theory Euler buckling equation: works well for slender rods Needs to be modified for smaller “slenderness ratios” (where the critical stress for Euler buckling is at least half the yield strength) 7 Summary L 2 E Critical slenderness ratio: e = r 0.5 gYc Euler buckling (high slenderness ratio): LL 2 E EI If ee : = or P = 2 rr cr 2 cr L2 gg c (Lreg) e Johnson bucklingI (low slenderness ratio): r = 2 g Lr LLeeA ( eg) If : =−1 rr cr2 Y gg c 2 Lr ( eg)c with radius of gyration 8 Summary Effective length from the boundary conditions: Pinned- Pinned- Fixed- LL= LL= 0.7 FixedLL=- 0.5 pinned fixed e fixede e LL= 2 free e 9 Example 18.1 Determine the critical buckling load Pcr of a steel pipe column that has a length of L with a tubular cross section of inner radius ri and thickness t.
    [Show full text]
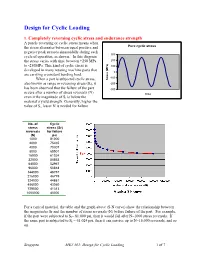
  • Design for Cyclic Loading, Soderberg, Goodman and Modified Goodman's Equation
    Design for Cyclic Loading 1. Completely reversing cyclic stress and endurance strength A purely reversing or cyclic stress means when the stress alternates between equal positive and Pure cyclic stress negative peak stresses sinusoidally during each 300 cycle of operation, as shown. In this diagram the stress varies with time between +250 MPa 200 to -250MPa. This kind of cyclic stress is 100 developed in many rotating machine parts that 0 are carrying a constant bending load. -100 When a part is subjected cyclic stress, Stress (MPa) also known as range or reversing stress (Sr), it -200 has been observed that the failure of the part -300 occurs after a number of stress reversals (N) time even it the magnitude of Sr is below the material’s yield strength. Generally, higher the value of Sr, lesser N is needed for failure. No. of Cyclic stress stress (Sr) reversals for failure (N) psi 1000 81000 2000 75465 4000 70307 8000 65501 16000 61024 32000 56853 64000 52967 96000 50818 144000 48757 216000 46779 324000 44881 486000 43060 729000 41313 1000000 40000 For a typical material, the table and the graph above (S-N curve) show the relationship between the magnitudes Sr and the number of stress reversals (N) before failure of the part. For example, if the part were subjected to Sr= 81,000 psi, then it would fail after N=1000 stress reversals. If the same part is subjected to Sr = 61,024 psi, then it can survive up to N=16,000 reversals, and so on. Sengupta MET 301: Design for Cyclic Loading 1 of 7 It has been observed that for most of engineering materials, the rate of reduction of Sr becomes negligible near the vicinity of N = 106 and the slope of the S-N curve becomes more or less horizontal.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • Hydraulics Manual Glossary G - 3
    Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B.
    [Show full text]
  • 4.2 Failure Criteria
    4.2 Failure Criteria The determination of residual strength for uncracked structures is straightforward because the ultimate strength of the material is the residual strength. A crack in a structure causes a high stress concentration resulting in a reduced residual strength. When the load on the structure exceeds a certain limit, the crack will extend. The crack extension may become immediately unstable and the crack may propagate in a fast uncontrollable manner causing complete fracture of the component. Figure 4.2.1 illustrates the results obtained from a series of tests conducted on a lug geometry containing a crack. The lug geometry shown in Figure 4.2.1a is a single-load-path structure. Figure 4.2.1b indicates that the cracks in each of the three tests extended abruptly at a critical level of load, which is noted to be a function of a crack length. The crack length-critical load level data shown in Figure 4.2.1b provide the basis for establishing the residual strength capability curve. The locus of critical load levels as a function of crack length is shown in Figure 4.2.1c, where the residual strength capability of the lug structure is shown to decrease with increasing crack length. Figure 4.2.1. Description of Crack Geometry and Residual Strength Results Considering the preceding in terms of applied stress (σ) rather than load gives the σ versus a and σc versus ac plots as shown in Figure 4.2.2 a and b. Schematically, the plots exhibit the same abrupt fracture behavior as the curves presented in Figure 4.2.1.
    [Show full text]
  • High Strength Steels
    Automotive Worldwide Product Offer for US High Strength Steels Grade Availability ArcelorMittal offers the automotive industry a family of HI FORM (HF) high-strength steels with yield strength grades ranging from 250 to 550 MPa and tensile strength grades from 340 to 590 MPa. Yield Strength Grades Yield Strength Hot Rolled Cold Rolled Uncoated Uncoated EG HDGI HDGA 250 MPa - Yes Yes Yes - 300 MPa Yes Yes Yes - - 350 MPa Yes Yes Yes Yes Yes 400 MPa - Yes Yes Yes Yes 480, 500 MPa - Yes Yes - - 550 MPa - Yes Yes - - Tensile Strength Grades Tensile Strength Hot Rolled Cold Rolled Uncoated Uncoated EG HDGI HDGA 340 MPa - Yes Yes - Yes 370 MPa - Yes Yes - - 390 MPa - Yes Yes - Yes 440 MPa - Yes Yes - Yes 590 MPa Dev Yes - - Yes EG: Electrogalvanized HDGI: Hot-Dip-Galvanized HDGA: Hot-Dip-Galvannealed Yes: Products Commercially Available Note: Information contained in this document is subject to change. Please contact our sales team whenever you place an order to 1 ensure that your requirements are fully met. Please contact us if you have a specific requirement that is not included in the range of products and services covered by this document. Update: August 2009 Dev: Products are under development or in limited production. Please inquire about the status and availability of these products. Product Characteristics High strength steels are mainly used for structural applications and are hence also called structural steels. They can be produced with or without addition of small amount of microalloying elements. High strength low alloy steels, commonly referred to as HSLA steels, are produced using microalloying elements like Cb, Ti, Mo, V etc.
    [Show full text]
  • An Investigation of the Low Temperature Creep Deformation Behavior of Titanium Grade 7 and Grade 5 Alloys—Progress Report with Preliminary Results
    AN INVESTIGATION OF THE LOW TEMPERATURE CREEP DEFORMATION BEHAVIOR OF TITANIUM GRADE 7 AND GRADE 5 ALLOYS—PROGRESS REPORT WITH PRELIMINARY RESULTS Prepared for U.S. Nuclear Regulatory Commission Contract NRC–02–02–012 Prepared by S. Ankem,1 P.G. Oberson,2 R.V. Kazban,3 K.T. Chiang,3 L.F. Ibarra,3 and A.H. Chowdhury3 1Ankem Technology, Inc. Silver Spring, Maryland 2U.S. Nuclear Regulatory Commission Office of Nuclear Material Safety and Safeguards Division of High-Level Waste Repository Safety Washington, DC 3Center for Nuclear Waste Regulatory Analyses San Antonio, Texas August 2007 ABSTRACT The U.S. Nuclear Regulatory Commission (NRC) is interacting with U.S. Department of Energy (DOE) to gain insight into the potential geologic repository at Yucca Mountain, Nevada. In the design DOE is currently considering, the radioactive materials would be encapsulated in waste packages and emplaced in drifts (tunnels) below the surface. Subsequently, drip shields, primarily made of Titanium Grade 7 and Grade 24, would be placed over the waste packages to protect them from seepage and rockfall. If drift degradation occurs, drip shields would be subjected to impact loads due to the falling rock and static and dynamic (seismic) loads resulting from accumulated rockfall rubble. In the case when the accumulated rockfall rubble does not result in static loads high enough to produce immediate failure of the drip shield, the drip shield components would be subjected to permanent static loading, leading to stresses that may approach or exceed the yield stress of the drip shield materials. Titanium Grade 7 and Grade 5 (surrogate of Titanium Grade 24) were investigated for low temperature {from 25 to 250 °C [77 to 482 °F]} tensile and creep behavior.
    [Show full text]
  • Very High Cycle Fatigue of Engineering Materials
    Faculty of Technology and Science Materials Engineering Vitaliy Kazymyrovych Very high cycle fatigue of engineering materials (A literature review) Karlstad University Studies 2009:22 Vitaliy Kazymyrovych Very high cycle fatigue of engineering materials (A literature review) Karlstad University Studies 2009:22 Vitaliy Kazymyrovych. Very high cycle fatigue of engineering materials - A literature review Research Report Karlstad University Studies 2009:22 ISSN 1403-8099 ISBN 978-91-7063-246-4 © The Author Distribution: Faculty of Technology and Science Materials Engineering SE-651 88 Karlstad +46 54 700 10 00 www.kau.se Printed at: Universitetstryckeriet, Karlstad 2009 Very high cycle fatigue of engineering materials (A literature review) V.Kazymyrovych* Department of Materials Engineering, Karlstad University SE-651 88, Sweden * Email address: [email protected] Abstract This paper examines the development and present status of the Very High Cycle Fatigue (VHCF) phenomenon in engineering materials. The concept of ultrasonic fatigue testing is described in light of its historical appearance covering the main principles and equipment variations. The VHCF behaviour of the most important materials used for very long life applications is presented, with particular attention paid to steels. In section 3 the VHCF properties of titanium-, nickel-, aluminium- and magnesium alloys are described. Furthermore, the typical fatigue behaviour and mechanisms of pure metals are presented. Section 4 examines the VHCF properties of various types of steels e.g. low carbon steel, spring steel, stainless steel, bearing steel as well as tool steel. In addition to this, the main material defects that initiate VHCF failure are examined in this study. Furthermore, the different stages characteristic for fatigue crack development in VHCF are described in section 5 in terms of relative importance and sequence.
    [Show full text]