DOCSLIB.ORG

Boron-Proton Nuclear-Fusion Enhancement Induced in Boron-Doped Silicon Targets by Low-Contrast Pulsed Laser

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Boron-Proton Nuclear-Fusion Enhancement Induced in Boron-Doped Silicon Targets by Low-Contrast Pulsed Laser PHYSICAL REVIEW X 4, 031030 (2014) Boron-Proton Nuclear-Fusion Enhancement Induced in Boron-Doped Silicon Targets by Low-Contrast Pulsed Laser † A. Picciotto,1,* D. Margarone,2, A. Velyhan,2 P. Bellutti,1 J. Krasa,2 A. Szydlowsky,3,4 G. Bertuccio,5 Y. Shi,5 A. Mangione,6 J. Prokupek,2,7 A. Malinowska,4 E. Krousky,8 J. Ullschmied,8 L. Laska,2 M. Kucharik,7 and G. Korn2 1Micro-Nano Facility, Fondazione Bruno Kessler, 38123 Trento, Italy 2Institute of Physics ASCR, v.v.i. (FZU), ELI-Beamlines Project, 182 21 Prague, Czech Republic 3Institute of Plasma Physics and Laser Microfusion, 01-497 Warsaw, Poland 4National Centre for Nuclear Research, 05-400 Otwock, Poland 5Politecnico di Milano, Department of Electronics Information and Bioengineering, 22100 Como, Italy 6Institute of Advanced Technologies, 91100 Trapani, Italy 7Czech Technical University in Prague, FNSPE, 115 19 Prague, Czech Republic 8Institute of Plasma Physics of the ASCR, PALS Laboratory, 182 00 Prague, Czech Republic (Received 12 January 2014; revised manuscript received 1 April 2014; published 19 August 2014) We show that a spatially well-defined layer of boron dopants in a hydrogen-enriched silicon target allows the production of a high yield of alpha particles of around 109 per steradian using a nanosecond, low-contrast laser pulse with a nominal intensity of approximately 3 × 1016 Wcm−2. This result can be ascribed to the nature of the long laser-pulse interaction with the target and with the expanding plasma, as well as to the optimal target geometry and composition. The possibility of an impact on future applications such as nuclear fusion without production of neutron-induced radioactivity and compact ion accelerators is anticipated. DOI: 10.1103/PhysRevX.4.031030 Subject Areas: Nuclear Physics, Plasma Physics I. INTRODUCTION It is well known both from theoretical calculations and The 11Bðp; αÞ2α nuclear-fusion reaction was first stud- experimental measurements (performed with standard ied in the 1930s by Oliphant and Rutherford [1]. Interest accelerators) that the reaction has a main channel with a from the scientific community in this reaction is now maximum cross section for protons with energies of increasing due to the possibility of producing energetic 600–700 keV [7–9]. Typically, this channel generates alpha alpha particles without neutron generation, which may particles with an energy distribution ranging from 2.5 to allow the building of an “ultraclean” nuclear-fusion reactor 5.5 MeV and a maximum at around 4.3 MeV (α1). [2–4]. The first experimental demonstration of a laser- A secondary channel generating alpha particles in the 11 driven Bðp; αÞ2α reaction was performed using the energy range 6–10 MeV can also be present (α2) [5,10,11]. interaction of a high-intensity (around 2 × 1018 Wcm−2) picosecond laser pulse with a boron-enriched polymeric II. METHODS target. This experiment gave an alpha-particle yield per pulse of around 103 per steradian [5]. Recently, a much The experiment is performed at the Prague Asterix Laser higher particle yield (around 107 per steradian) has been System (PALS) facility in Prague [12], where a kJ-class reported by using a more sophisticated experimental setup (around 500 J in our experiment), subnanosecond (0.3-ns and similar laser intensity [6]. full width at half maximum, FWHM), linearly polarized Our experiment aims to produce a high yield of alpha laser is used to irradiate massive silicon targets. The laser 11 particles by triggering the proton (p)-boron ( B) nuclear pulse is focused in an 80-μm focal spot by an f=2 spherical reaction: lens to reach a nominal intensity of 3 × 1016 Wcm−2 on the 6 −5 11B þ p → 3α þ 8.7 MeV: ð1Þ target surface in vacuum conditions of 10 –10 mbar. The incidence angle between the laser-beam axis and the target normal is 30°. The nominal laser intensity is low compared *Corresponding author. with the high intensities achievable with picosecond and [email protected] femtosecond laser systems. Nevertheless, recent experi- † Corresponding author. ments on laser-driven ion beams performed at PALS have [email protected] shown maximum proton energies of a few MeV [13] which are typical for laser intensities of 5 × 1018–1019 Wcm−2 Published by the American Physical Society under the terms of the Creative Commons Attribution 3.0 License. Further distri- when shorter pulses are used [14]. bution of this work must maintain attribution to the author(s) and Most of these targets were previously enriched with the published article’s title, journal citation, and DOI. hydrogen and boron atoms through thermal annealing and 2160-3308=14=4(3)=031030(8) 031030-1 Published by the American Physical Society A. PICCIOTTO et al. PHYS. REV. X 4, 031030 (2014) 50-keV ion-implantation doping processes performed at the (a) Microtechnologies Laboratory (MTLab) at Fondazione Bruno Kessler in Trento [15,16]. Thus, well-known chemical-physical processes used in microelectronics help us to develop the idea of using boron-hydrogen-silicon targets for triggering a specific fusion reaction by precisely control- ling the concentration and implantation or diffusion depth of the doping element. Here, we report mainly the results obtained by laser irradiation of massive silicon samples (0.5 mm thick) that are implanted with boron atoms (amu ¼ 11) located at a depth of 190 nm and having a 1022 −3 concentration of about cm . (The boron layer is (b) approximately 100 nm thick.) The concentration of hydrogen 100 in the samples is increased through a thermal process 10-1 where hydrogen atoms diffusing into the silicon matrix -2 can link to it by forming Si-H bonds, which neutralize 10 0 I II III the silicon dangling bonds [17–20], thus reaching a concen- 10-3 20 −3 tration higher than 10 cm . Silicon samples where boron -4 [a.u.] 10 L I atoms are homogenously diffused into the substrate via the -5 thermal annealing process (1 h at 1000 °C) are also fabricated 10 -6 E (0 ns,1 ns) = 1.68 mJ and irradiated. In the latter case, the B atoms are distributed in 10 L -7 E (1 ns,1.85 ns) = 56 J a much thicker layer, starting from the sample surface up to a 10 L E (1.85 ns, 2.15 ns) = 488 J L certain depth (>10 μm), resulting in lower local boron -8 20 −3 10 concentration (approximately 10 cm ). These targets -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 τ [ns] are irradiated in a series of measurements at the beginning L of the experiment to be later compared with the results obtained with the implanted samples. Furthermore, silicon FIG. 1. (a) Experimental setup. T is the target, p is the proton “pure” samples (not artificially hydrogenated and without beam, α is the alpha-particle beam, PM-355 is the nuclear-track boron doping) are also irradiated for comparison. detector, TP is the Thomson-parabola spectrometer, MCP is the Ion analyzers, such as a Thomson-parabola (TP) spec- microchannel plate, and SiC is the silicon-carbide detector. The angles are measured with respect to the target normal. (b) Laser trometer, time-of-flight (TOF) silicon-carbide (SiC) I τ detectors [21–23], and solid-state nuclear-track detectors intensity ( L) against time ( L) in arbitrary units. The laser-energy content in different time windows is reported in the legend. of PM-355 type [24,25], are used to detect and identify the produced proton and alpha-particle beams and measure their energy distribution in various directions with respect laser-absorption modeling. The simulations shown in this to the target normal. A detailed description of the exper- paper are performed in the Lagrangian regime; thus, the imental setup is sketched in Fig. 1(a). layers of the targets remain separated throughout the whole The ns-long laser-pulse temporal shape is reported in simulation. The initial computational mesh is adjusted to Fig. 1(b). Although approximately 500 J are contained in the layered targets using a finer mesh resolution at the target the main pulse (0.3 ns at FWHM), the residual laser energy surface. The simulations are stopped after 1.85 ns [see (about 100 J) is stored in the nanosecond pedestal. (Around Fig. 1(b) as a reference]. The simulations are performed by 50 J of the pulse energy comes before the maximum- considering different target geometries: (a) a B-implanted intensity peak is reached.) Figure 1(b) shows the presence layer in a Si substrate with the above-described character- of three intensity regions: 0-I represents the low-intensity istics, (b) a B-diffused layer in a Si substrate with the 10 −2 (3 × 10 Wcm ) laser precursor, I-II is the high- above-described characteristics, and (c) a B layer deposited 15 −2 intensity (10 Wcm ) prepulse, and II-III is the high- on a Si-substrate surface with the same atomic concen- 16 −2 intensity (nominally 3 × 10 Wcm ) main pulse. tration as in (a). The comparison of the hydrodynamic A series of hydrodynamic simulations is performed by simulations corresponding to these three different geom- using a 2D Prague Arbitrary Lagrangian-Eulerian (PALE) etries is shown in Fig. 2, where z is the plasma-expansion code [26]. This code employs the compatible staggered longitudinal direction (parallel to the target normal) and r is Lagrangian numerical scheme [27] and a rezoning or the plasma-expansion transverse direction (parallel to the remapping mechanism improving the robustness of the target surface). The simulations take into account the time simulations. Thermal conductivity is treated by a mimetic evolution of the laser pulse in the range 1–1.85 ns.
Load more

Recommended publications
  • Assessing Potential Induced Radioactivity in Materials Processed with X-Ray Energy Above 5 Mev: Assessment Protocols and Practical Experience
    FERMILAB-PUB-20-562-DI Assessing potential induced radioactivity in materials processed with X-ray energy above 5 MeV: Assessment protocols and practical experience Hervé Michel1; Thomas Kroc2; Brian J. McEvoy 3; Deepak Patil4 Pierre Reppert5; Mark A. Smith6 1Director, Radiation Technology EMEAA, STERIS, Hogenweidstrasse 6, 4658 Däniken, Switzerland, [email protected] 2Applications Physicist for Technology Development, Fermilab, Batavia, Illinois, USA, [email protected] 3Senior Director Global Technologies, STERIS, IDA Business & Technology Park, Tullamore, County Offaly, R35 X865, Ireland, [email protected] 4Senior Director, Radiation Technology, 1880 Industrial Drive, Libertyville, IL 60048 [email protected] 5Validation Manager, STERIS, Hogenweidstrasse 6, 4658 Däniken, Switzerland, [email protected] 6Managing Director, Ionaktis, LLC, PO Box 11599, Charlotte, NC 28220 USA [email protected] Abstract In accordance with ISO11137-1 section 5.1.2, ‘the potential for induced radioactivity in product shall be assessed’. This article describes how compliance to this requirement may be achieved using qualified test methods. Materials of consideration are conceptually discussed. Results of testing conducted on products processed with a 7.5 MeV X-ray irradiation process are provided. As X-ray becomes more widely used in healthcare sterilization, having standard assessment protocols for activation coupled with a shared database of material test results will benefit all healthcare product manufacturers seeking to avail of this innovative technology. This manuscript has been authored by Fermi Research Alliance, LLC under Contract No. DE-AC02-07CH11359 with the U.S. Department of Energy, Office of Science, Office of High Energy Physics. 1. Introduction Radioactive material of natural origin is ubiquitous in nature, widely varying in type and amount.
    [Show full text]
  • Simulation of Induced Radioactivity for a Heavy Ion Medical Machine
    Chinese Physics C Vol. 38, No. 11 (2014) 118201 Simulation of induced radioactivity for a heavy ion medical machine XU Jun-Kui(Md¿)1;2 SU You-Wu(kÉ)2;1) LI Wu-Yuan(oÉ)2 MAO Wang(f!)2 XIA Jia-Wen(gZ©)2 CHEN Xi-Meng(Ú)1 YAN Wei-Wei(î)2 XU Chong(MÇ)2 1 School of Nuclear Science and Technology, Lanzhou University, Lanzhou 730000, China 2 Institute of Modern Physics, Chinese Academy of Science, Lanzhou 730000, China Abstract: The radioactivity induced by carbon ions of the Heavy Ion Medical Machine (HIMM) was studied to asses its radiation protection and environmental impact. Radionuclides in the accelerator component, and in the cooling water and air at the target area, which are induced from primary beam and secondary particles, are simulated by FLUKA Monte Carlo code. It is found that radioactivity in the cooling water and air is not very important at the required beam intensity and energy that is needed for treatment, while radionuclides in the accelerator component may cause some problems for maintenance work and, therefore, a suitable cooling time is needed after the machine is shut down. Key words: radioactivity, HIMM, heavy ion PACS: 07.89.+b, 28.41.Qb DOI: 10.1088/1674-1137/38/11/118201 1 Introduction back to the early period when Curie and Joliot found the activation reaction in 1934 [4]. In recent years, improve- Nowadays, radiation therapy is an important means ments of the accelerator have meant that more kinds of tumor treatment. More than 50% of all patients with of particles, of a higher energy can be accelerated and, localized malignant tumors are treated with radiation [1].
    [Show full text]
  • X Rays and Radioactivity : a Complete Surprise
    ÏLABORATOIRE ATIONAL ATURNE 91191 Gif-$ur-Yvette Cedex France X rays and Radioactivity : a complete surprise Pierre Radvanyi (Laboratoire National Saturne, 91191 Gif-sur-Yvette Cedex) and Monique Bordry (Musée et Archives de l'Institut du Radium, 75231 Paris Cedex 05) Contribution to the Conference on LHS/FH/95-05 the "Emergence of Modem Physics" W - ™W>™ Berlin, 22-24 March 1995 Centre National de la Recherche Scientifique OGO Commissariat à l'Energie Atomique 3>HÉ * **«*«» *r ILABORATOIRE ATIONAL ATURNE 91191 Gif-sur-Yvette Cedex France X rays and Radioactivity : a complete surprise Pierre Radvanyi (Laboratoire National Saturne, 91191 Gif-sur-Yvette Cedex) and Monique Bordry (Musée et Archives de l'Institut du Radium, 75231 Paris Cedex 05) Contribution to the Conference on the "Emergence of Modem Physics" ^ - ws/ph/95-os Berlin, 22-24 March 1995 m/fi Centre National de la Recherche Scientifique 093 Commissariat à l'Energie Atomique Berin, 23 March 1995 X rays and radioactivity : a complete surprise Pierre Radvanyi Laboratoire National Saturne, 91191 Gif-sur-Yvette Cedex and Monique Bordry Musée et Archives de l'Institut du Radium, 75231 Paris Cedex 05 Abstract The discoveries of X rays and of radioactivity came as complete experimental surprises; the physicists, at that time, had no previous hint of a possible structure of atoms. It is difficult now, knowing what we know, to replace ourselves in the spirit, astonishment and questioning of these years, between 1895 and 1903. The nature of X rays was soon hypothesized, but the nature of the rays emitted by uranium, polonium and radhim was much more difficult to disentangle, as they were a mixture of different types of radiations.
    [Show full text]
  • 28 Neutron Activation Analysis (NAA) Predicting the Sensitivity of Neutron Activation Analysis (NAA)
    Neutron Activation and Activation Analysis 11/26/09 1 General 2 General Many nuclear reactions produce radioactive products. The most common of these reactions involve neutrons: Neutron + Target Nuclide → Activation Product 3 General Important Applications/Issues Associated with Neutron Activation 1. Neutron Activation Analysis (NAA) This is an extraordinarily powerful technique for identifying and quantifying various elements (and nuclides) in a sample. 2. Neutron Fluence Rate (Flux) Measurements Neutron fluence rates in reactors or other neutron sources can be measured by exposing targets (e.g., metal foils) to the neutrons and measuring the induced activity. 4 General Important Applications/Issues Associated with Neutron Activation 3. Dosimetry Following Criticality Accidents The induced activity in objects or individuals following a criticality accident can be used to estimate the doses to these individuals. 4. Hazards from Induced Activity Induced radioactivity in the vicinity of intense neutron sources can constitute an exposure hazard. Examples of such sources include reactors, accelerators and, of course, nuclear explosions. 5 General Neutron Capture The most important reaction is neutron capture: Thermal neutrons are most likely to be captured. The target nuclide is usually, but not necessarily stable. If the product is radioactive, it is likely a beta emitter. The gamma ray, referred to as a prompt gamma or capture gamma, is typically of high energy. 6 General Neutron Capture Example: This is an exception to the generalization that the activation product is a beta emitter. Cr-51 decayyys by electron cap ture! The major prompt gamma rays: 749 keV produced 11.0% of the time 8512.1 keV produced 6.16% of the time 8484.0 keV produced 4.54% of the time 7 General Neutron-Proton Reaction Another potentially important reaction is the n-p reaction: The n-p reaction is most likely for fast neutrons and target nuclides with low atomic numbers.
    [Show full text]
  • Simulation of Induced Radioactivity for Heavy Ion Medical Machine XU Jun-Kui1,2 SU You-Wu1 LI Wu-Yuan1 MAO Wang1 XIA Jia-Wen1 CH
    Submitted to ‘Chinese Physics C’ Simulation of induced radioactivity for Heavy Ion Medical Machine XU Jun-Kui1,2 SU You-Wu1 LI Wu-Yuan1 MAO Wang1 XIA Jia-Wen1 CHEN Xi-Meng2 YAN Wei-Wei 1 XU Chong1 1 Institute of Modern Physics, Chinese Academy of Science, Lanzhou 730000, China 2 The School of Nuclear Science and Technology Lanzhou University, Lanzhou 73000, China Abstract：For radiation protection and environmental impact assessment purpose, the radioactivity induced by carbon ion of Heavy Ion Medical Machine (HIMM) was studied. Radionuclides in accelerator component, cooling water and air at target area which are induced from primary beam and secondary particles are simulated by FLUKA Monte Carlo code. It is found that radioactivity in cooling water and air is not very important at the required beam intensity and energy which is needed for treatment, radionuclides in accelerator component may cause some problem for maintenance work, suitable cooling time is needed after the machine are shut down. Key word：radioactivity, HIMM, heavy ion 1. Introduction Nowadays radiation therapy is an important mean of treatment of tumor, more than 50% of all patients with localized malignant tumors are treated with radiation [1]. Many accelerators are built for medical purpose, in which heavy ion therapy is the most advanced treatment technology, and start at Bevalac facility at LBL in 1975 [2], and now there are 4 countries had launched the practice of heavy ion therapy. IMP (the Institute of Modern Physics, Chinese Academy of Sciences) had been started the research of biological effect of radiation with middle energy heavy ions since 1993, and start superficial tumor treatment of clinical research with 80MeV/u carbon ion beam in 2006.
    [Show full text]
  • Use of Isotopes to Reduce Neutron-Induced Radioactivity and Augment Thermal Quality of the Environment of an Underground Nuclear Explosion
    Scholars' Mine Masters Theses Student Theses and Dissertations 1972 Use of isotopes to reduce neutron-induced radioactivity and augment thermal quality of the environment of an underground nuclear explosion Nathaniel Fred Colby Follow this and additional works at: https://scholarsmine.mst.edu/masters_theses Part of the Nuclear Engineering Commons Department: Recommended Citation Colby, Nathaniel Fred, "Use of isotopes to reduce neutron-induced radioactivity and augment thermal quality of the environment of an underground nuclear explosion" (1972). Masters Theses. 5056. https://scholarsmine.mst.edu/masters_theses/5056 This thesis is brought to you by Scholars' Mine, a service of the Missouri S&T Library and Learning Resources. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. USE OF ISOTOPES TO REDUCE NEUTRON-INDUCED RADIOACTIVITY AND AUGMENT THERMAL QUALITY OF THE ENVIRONMENT OF AN UNDERGROUND NUCLEAR EXPLOSION BY NATHANIEL FRED COLBY, 1936- A THESIS Presented to the Faculty of the Graduate School of the UNIVERSITY OF MISSOURI-ROLLA In Partial Fulfillment of the Requirements for the Degree MASTER OF SCIENCE IN NUCLEAR ENGINEERING 1972 T2713 43 pages c. I Approved by ~.If(~ (Advisor) ii ABSTRACT The use of isotopes to include radioactive waste pro­ ducts to reduce the neutron-induced activity of an under­ ground nuclear explosion and its application in the field of geothermal power stimulation is discussed. A shield com­ posed of selected isotopes surrounding a fusion device will capture excess neutrons producing isotopes with short half­ lives. Subsequent rapid decay will prolong the high temperature in the vicinity of the explosion and decrease the activity.
    [Show full text]
  • Radioactivity Induced by Neutrons: a Thermodynamic Approach to Radiative Capture
    RADIOACTIVITY INDUCED BY NEUTRONS: A THERMODYNAMIC APPROACH TO RADIATIVE CAPTURE Alberto De Gregorio* ABSTRACT œ When Enrico Fermi discovered slow neutrons, he accounted for their great efficiency in inducing radioactivity by merely mentioning the well-known scattering cross-section between neutrons and protons. He did not refer to capture cross-section, at that early stage. It is put forward that a thermodynamic approach to neutron-proton radiative capture then widely debated might underlie his early accounts. Fermi had already met with a similar approach, and repeatedly used it. In 2004, seven decades had elapsed since the artificial radioactivity was discovered. On January 15, 1934 it was announced that the activation of aluminium, boron, and magnesium by α-particles had been obtained in the Institut du Radium in Paris. Some weeks later, between the end of February and mid-March, two different laboratories in California showed that deutons and protons as well could induce radioactivity.1 On March 25, Enrico Fermi communicated that radioactivity was induced in fluorine and aluminium irradiated with neutrons. In October, a second, crucial discovery was made in the laboratories of the Regio Istituto Fisico in Rome: in many cases, neutrons might become more effective if they were slowed down through hydrogenous substances.2 That especially occurred when a nucleus œ particularly a heavy one œ became radioactive through a process known as —radiative capture“, absorbing a slowed-down neutron and promptly emitting a gamma ray. It is noteworthy that for some time Fermi, while discussing the effects of slowing down the neutrons, did not refer at all to reaction cross-section between neutrons and nuclei.
    [Show full text]
  • The Women Behind the Periodic Table Brigitte Van Tiggelen and Annette Lykknes Spotlight Female Researchers Who Discovered Elements and Their Properties
    COMMENT follow the Madelung rule. Although scan- differentiates it from calcium is a 3d one, even physicists and philosophers still need to step dium’s extra electron lies in its 3d orbital, though it is not the final electron to enter the in to comprehend the gestalt of the periodic experiments show that, when it is ionized, it atom as it builds up. table and its underlying physical explana- loses an electron from 4s first. This doesn’t In other words, the simple approach to tion. Experiments might shed new light, make sense in energetic terms — textbooks using the aufbau principle and the Made- too, such as the 2017 finding that helium say that 4s should have lower energy than 3d. lung rule remains valid for the periodic table can form the compound Na2He at very high Again, this problem has largely been swept viewed as a whole. It only breaks down when pressures11. The greatest icon in chemistry under the rug by researchers and educators. considering one specific atom and its occu- deserves such attention. ■ Schwarz used precise experimental pation of orbitals and ionization energies. spectral data to argue that scandium’s 3d The challenge of trying to derive the Eric Scerri is a historian and philosopher orbitals are, in fact, occupied before its 4s Madelung rule is back on. of chemistry at the University of California, orbital. Most people, other than atomic Los Angeles, California, USA. spectroscopists, had not realized this THEORIES STILL NEEDED e-mail: [email protected] before. Chemistry educators still described This knowledge about electron orbitals does 1.
    [Show full text]
  • UZ0603177 NEUTRON ACTIVATION ANALYSIS of PURE URANIUM USING PRECONCENTRATION Sadikov I.I., Rakhimov A.V., Salimov M.I., Zinov'ev
    The Sixth International Conference "Modern Problems of Nuclear Physics", September 19-22, 2006 MPNP'2006 INP-50 The nuclear-physical properties of bromine and radioisotopes of other elements with close half-lives, the influence of competitive nuclear reactions and interference lines have been studied. The optimization of temporary parameters of analysis has been carried out. Thus, the method for determination of Br, Au, Sm, La and Na in hydromineral raw materials by instrumental neutron activation analysis has been developed. The dry residue (after evaporation of 1 ml sample) is irradiated in vertical channel of nuclear reactor (neutron flux is lxl014 n/cm2 s) for 15 hours. The samples were measured (tmeas=400 sec) with Ge detector after 10-15 days of "cooling". The determination limits of elements are Br-0.8 mg/1; Au-0.7 u.g/1; Sm-0.1|j.g/l; La-15 ug/1; Na-2mg/l at this regime of analysis. The analysis for a number of industrial samples to determine these elements is carried out. The samples with enhanced industrial -valuable concentration of elements have been found. The correlation dependence between bromine and sodium contents is determined. The comparison of results for neutron activation analysis and chemical analysis methods has been carried out. It shows the satisfactory agreement between them. UZ0603177 NEUTRON ACTIVATION ANALYSIS OF PURE URANIUM USING PRECONCENTRATION Sadikov I.I., Rakhimov A.V., Salimov M.I., Zinov'ev V.G. Institute of Nuclear Physics, Tashkent, Uzbekistan Uranium and its compounds are used as nuclear fuel, and requirements for purity of initial uranium are very high.
    [Show full text]
  • INDUCED RADIOACTIVITY in ACCELERATORS M. Barbier a Lot of Attention Has Been Paid Recently to the Activation of Accelerators. Th
    INDUCED RADIOACTIVITY IN ACCELERATORS M. Barbier CERN INTRODUCTION which can indicate the exact dose in rads. Also, the detector used should be fairly omnidirectional, A lot of attention has been paid recently as radiation will come from all to the activation of accelerators. The radioactivity directions in a machine hall. induced by the flux of particles during the operation of the machine remains after the latter has stopped running. It constitutes a permanent danger to staff and restricts access to the equipment for operation, maintenance, repairs and alterations, in a way that is already being felt. It is beginning to be realized that it is the activation level that will set a practical limit to the beam intensities of future machines. Accelerators are intended for constantly changing experimental work, involving frequent modifications in parts of the machine itself. For a series of investigations the accelerator cannot be operated as a box delivering a beam of primary particles. Depending upon the type of experiments in view, one must expect to run into a «barrier of radioactivity» that will dictate the maximum intensity of the internal beam if the machine is to remain a useful nuclear physics tool. The principal methods for studying induced radioactivity will be outlined. These include measurements on a radioactive machine, experiments to establish the properties of various materials, and the calculation of radiation fields. Some experimental data collected at the CERN Synchro-Cyclotron will be given as an illustration. 1. ACCELERATOR ACTIVATION SURVEY The first experiment to perform in order Fig. 1. Lead protected counter. to study induced radioactivity on an accelerator is to measure the radiation level and The next step is to find out which parts its decay with time at different points in the of the machine are most active.
    [Show full text]
  • Activation.Pdf
    Induced Radioactivity 7th FLUKA Course NEA Paris, Sept.29-Oct.3, 2008 FLUKA-Implementation – History - 1 1995 – Offline evolution: An offline code (usrsuwev.f) is distributed together with FLUKA, which allows the offline computation of the time evolution of a radionuclide inventory obtained with RESNUCLE for arbitrary irradiation profiles and decay times. 2002 – Two step method: The offline code has been adapted for online use, each time a residual nucleus is produced during a particle cascade. This allows storing information on radio- nuclides for certain irradiation parameter and cooling times into an external file. This information can then be read in order to compute residual dose rates due to induced radioactivity (two-step method). Results were benchmarked in numerous irradiation experiments. 2004 - Online: This capability has been implemented into FLUKA with an exact analytical solution of the Bateman equations describing activity build-up and decay during irradiation and cooling down, for arbitrary irradiation conditions. 7th FLUKA Course, Paris Sept.29-Oct.3, 2008 2 FLUKA-Implementation – History - 2 The generation and transport of decay radiation (limited to , -, and + emissions for the time being) is now possible during the same simulation which produces the radio-nuclides (one-step method). A dedicated database of decay emissions has been written, using mostly information obtained from NNDC, sometimes supplemented with other data and checked for consistency. As a consequence, results for production of residuals, their time evolution and residual doses due to their decays can now be obtained in the same run, for an arbitrary number of decay times and for a given irradiation profile.
    [Show full text]
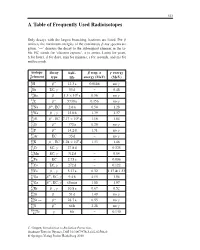
  • A Table of Frequently Used Radioisotopes
    323 A Table of Frequently Used Radioisotopes Only decays with the largest branching fractions are listed. For β emitters the maximum energies of the continuous β-ray spectra are given. ‘→’ denotes the decay to the subsequent element in the ta- ble. EC stands for ‘electron capture’, a (= annus, Latin) for years, h for hours, d for days, min for minutes, s for seconds, and ms for milliseconds. isotope decay half- β resp. α γ energy A Z element type life energy (MeV) (MeV) 3 β− . γ 1H 12 3a 0.0186 no 7 γ 4Be EC, 53 d – 0.48 10 β− . × 6 γ 4Be 1 5 10 a 0.56 no 14 β− γ 6C 5730 a 0.156 no 22 β+ . 11Na ,EC 2 6a 0.54 1.28 24 β− γ . 11Na , 15 0h 1.39 1.37 26 β+ . × 5 13Al ,EC 7 17 10 a 1.16 1.84 32 β− γ 14Si 172 a 0.20 no 32 β− . γ 15P 14 2d 1.71 no 37 γ 18Ar EC 35 d – no 40 β− . × 9 19K ,EC 1 28 10 a 1.33 1.46 51 γ . 24Cr EC, 27 8d – 0.325 54 γ 25Mn EC, 312 d – 0.84 55 . 26Fe EC 2 73 a – 0.006 57 γ 27Co EC, 272 d – 0.122 60 β− γ . 27Co , 5 27 a 0.32 1.17 & 1.33 66 β+ γ . 31Ga , EC, 9 4h 4.15 1.04 68 β− γ 31Ga , EC, 68 min 1.88 1.07 85 β− γ .
    [Show full text]