Does Roger Federer Feel the Pressure in Close Matches?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

P20 Layout 1
Perrin spices up Palestinian China challenge team aim for knockout stage THURSDAY, JANUARY 8, 201518 19 Smith joins greats as Aussies pressure India Page 16 DOHA: Novak Djokovic of Serbia returns the ball to Sergiy Stakhovsky of Ukraine during the Qatar ATP Open Tennis tournament. — AP Djokovic eases into Qatar q-finals DOHA: World number one Novak Djokovic took a sig- focus and nicely controlled aggression. “I have never when they are presented and also be prepared for at Seventh seed Karlovic fired 17 aces in a straight sets nificant step towards winning a tournament in the played here before but I shall definitely be coming back least one tie-break.” Djokovic’s performance on win over Nikoloz Basilashvili, a qualifier from Georgia, opening week of the season for the first time in eight next year,” said the man who is playing in the first week Wednesday was not perfect. which carried him to a career total of 9,041. years when he brushed aside the challenge of Sergiy of the ATP World Tour for only the third time. “And I’m Several times he turned his head away in irritation That is not only the most aces of any active player Stakhovsky. feeling better.” after mistiming with his ground strokes. But he always but Karlovic is now a mere 33 behind Andy Roddick, the The Serbian’s 6-2, 6-1 win over the Ukrainian carried That medical news is probably the most important rectified the damage, and often dealt with Stakhovsky’s former US Open champion whose total is the second him to the quarter-finals of the Qatar Open and enabled piece of progress for the man who has won the net rushes with calmly venomous counter-punching, highest of all time. -

FEATURED MEN's MATCHES – in Order of Play by Court
2015 US OPEN Flushing Meadows, New York, USA | August 31 – September 13, 2015 Draw Size: S-128, D-64 | $42.3 million | Hard www.usopen.org DAY FIVE NOTES | Friday, September 4, 2015 FEATURED MEN’S MATCHES – In Order of Play by Court Arthur Ashe Stadium: (1) Novak Djokovic (SRB) vs. (25) Andreas Seppi (ITA) Djokovic Leads 10-0 (8) Rafael Nadal (ESP) vs (32) Fabio Fognini (ITA) Nadal Leads 5-2 Louis Armstrong Stadium: (9) Marin Cilic (CRO) vs. Mikhail Kukushkin (KAZ) Tied 1-1 (7) David Ferrer (ESP) vs. (27) Jeremy Chardy (FRA) Ferrer Leads 7-1 Grandstand: (19) Jo-Wilfried Tsonga (FRA) vs. Sergiy Stakhovsky (UKR) Tsonga Leads 4-0 (10) Milos Raonic (CAN) vs. (18) Feliciano Lopez (ESP) Tied 3-3 Court 17: (26) Tommy Robredo (ESP) vs. Benoit Paire (FRA) Paire Leads 2-1 (14) David Goffin (BEL) vs. (23) Roberto Bautista Agut (ESP) Bautista Agut Leads 1-0 DAY FIVE HIGHLIGHTS The third round of the US Open begins on Friday with three players in action who have yet to be broken during the tournament: No. 1 Novak Djokovic (24 service games), No. 10 seed Milos Raonic (36 games) and No. 19 seed Jo-Wilfried Tsonga (26 games). Also on the schedule are two-time champion Rafael Nadal, two-time semi- finalist David Ferrer and ‘13 quarter-finalist Tommy Robredo, who are three of six Spaniards in the third round. On Ashe, Djokovic takes a near-perfect record against Italian opponents (30-1) into his 3R match with No. 25 seed Andreas Seppi. The 2011 US Open champion is 10-0 vs. -

AEGON OPEN NOTTINGHAM: DAY 4 NOTES Wednesday, June 24, 2015
AEGON OPEN NOTTINGHAM: DAY 4 NOTES Wednesday, June 24, 2015 Nottingham, England | June 21 – 27, 2015 Draw: S-48, D-16 | Prize Money: €644,065 | Surface: Grass ATP Info: Tournament Info: ATP PR & Marketing: www.ATPWorldTour.com www.lta.org.uk Thomas Troxler: [email protected] @ATPWorldTour @BritishTennis #aegonopen #nottingham Press Room: +44 333 011 1030 facebook.com/ATPWorldTour facebook.com/britishtennislta NINE OF TOP 16 SEEDS LEAD WAY IN THIRD ROUND ACTION DAY 4 PREVIEW: Nine of the Top 16 seeds are into the third round on Wednesday at the Aegon Open Nottingham with No. 2 Gilles Simon, No. 3 Feliciano Lopez, No. 4 Leonardo Mayer and No. 5 Pablo Cuevas leading the way. There are three seeds in the top half of the draw and six in the bottom. In the opening match on Centre Court, former World No. 8 Marcos Baghdatis, who upset top seed David Ferrer, takes on German wild card Alexander Zverev for the first time. In the next match on, Cuevas and last year’s semi-finalist No. 12 Sam Querrey, square off for the first time. In the third match, No. 14 Joao Sousa of Portugal and No. 2 /’13 runner-up Simon meet for the third time (tied 1-1). This is their first meeting on grass. In the final match on, Yen-Hsun Lu of Chinese Taipei looks for his first win (0-2) against No. 3 seed/ two-time reigning champion Lopez. There are two matches on Court 1 and Court 2 with four seeds in action. th PAES TEAMS WITH 100 PARTNER – The top seeds in the doubles draw are Marcel Granollers & Leander Paes, who are teaming up together for the first time. -

ATP Challenger Tour by the Numbers
ATP MEDIA INFORMATION Updated: 20 September 2021 2021 ATP CHALLENGER BY THE NUMBERS Match Wins Leaders W-L Titles 1) Benjamin Bonzi FRA 49-11 6 2) Tomas Martin Etcheverry ARG 38-13 2 3) Zdenek Kolar CZE 29-18 3 4) Holger Rune DEN 28-7 3 5) Kacper Zuk POL 26-11 1 Nicolas Jarry CHI 26-12 1 7) Sebastian Baez ARG 25-5 3 Altug Celikbilek TUR 25-10 2 Juan Manuel Cerundolo ARG 25-10 3 Tomas Barrios Vera CHI 25-11 1 11) Jenson Brooksby USA 23-3 3 Gastao Elias POR 23-12 1 Win Percentage Leaders W-L Pct. Titles 1) Jenson Brooksby USA 23-3 88.5 3 2) Sebastian Baez ARG 25-5 83.3 3 3) Benjamin Bonzi FRA 49-11 81.7 6 4) Holger Rune DEN 28-7 80.0 3 5) Zizou Bergs BEL 19-6 76.0 3 6) Federico Coria ARG 18-6 75.0 1 7) Tomas Martin Etcheverry ARG 38-13 74.5 2 8) Arthur Rinderknech FRA 18-7 72.0 1 Botic van de Zandschulp NED 18-7 72.0 0 *Minimum 20 matches played* Singles Title Leaders ----- By Surface ----- Player Total Clay Grass Hard Carpet Benjamin Bonzi FRA 6 1 5 Sebastian Baez ARG 3 3 Zizou Bergs BEL 3 1 2 Jenson Brooksby USA 3 1 2 Juan Manuel Cerundolo ARG 3 3 Tallon Griekspoor NED 3 3 Zdenek Kolar CZE 3 3 Holger Rune DEN 3 3 Franco Agamenone ITA 2 2 Daniel Altmaier GER 2 2 Altug Celikbilek TUR 2 2 Mitchell Krueger USA 2 2 Tomas Martin Etcheverry ARG 2 2 Mats Moraing GER 2 2 Carlos Taberner ESP 2 2 Bernabe Zapata Miralles ESP 2 2 53 tied with 1 title each Winners by Age: 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 0 0 6 7 8 4 7 10 13 13 4 3 7 5 3 1 0 3 0 1 0 1 0 0 Youngest Final: Juan Manuel Cerundolo (19) d. -

Tournament Notes
TOURNAMENT NOTES as of August 1, 2013 THE COMERICA BANK CHALLENGER APTOS, CA • AUGUST 3–11 USTA PRO CIRCUIT RETURNS TO APTOS TOURNAMENT INFORMATION The Comerica Bank Challenger is returning to Aptos for the 26th year. It is the second- Site: Seascape Sports Club – Aptos, Calif. longest running men’s event on the USTA Pro Circuit, trailing only Little Rock, Ark., which Websites: www.seascapesportsclub.com Bo Mon Kwon has been taking place for 32 years. The procircuit.usta.com tournament increased its prize money from Facebook: USTA $100,000 Seascape $75,000 to $100,000 last year and is one Comerica Bank Challenger of six $100,000 Challengers on the USTA Pro Circuit calendar this year. It is also one of Twitter: @ssconline nine USTA Pro Circuit men’s events held in Qualifying Draw Begins: Saturday, August 3 California. The tournament is the last USTA Pro Circuit event before the US Open. Main Draw Begins: Monday, August 5 Main Draw: 32 Singles / 16 Doubles Aptos is also the last of four consecutive men’s hard-court tournaments—joining Surface: Hard / Outdoor $50,000 Challengers in Binghamton, Prize Money: $100,000 N.Y., and Lexington, Ky., and a $100,000 Challenger in Vancouver, Canada, all held Tournament Director: over the previous three weeks—that are Judy Welsh, (831) 251-0004 part of a series of events that will determine A two-time NCAA singles champion for USC, [email protected] the recipient of a men’s singles wild card Steve Johnson is the defending champion in Aptos. In 2012, he reached the third round of Tournament Press Contact: into the 2013 US Open. -

Grab Campus Jobs
THE The Independent Newspaper Serving Notre Dame and Saint Mary's OLUME 41: ISSUE 7 - WEDNESDAY, AUGUST 30,2006 NDSMCOBSERVER.COM University plans Eddy Street Commons 'Tradition' Kite]," he said Tuesday. By KATIE PERRY "That process has not been Assistant News Editor concluded yet." Shirt sales Hakanen said there is "no • • Notre Dame is forging particular time frame" for ahead with plans to develop when the University plans to Increasing DPAC a retail and residential dis reach an agreement with trict just south of campus the developer. and has confirmed talks "We will finish and make Fans embrace year's with a preferred developer an announcement once for -the project, University we've worked our way design, organizers say officials said Tuesday.. through the issues," he said. Greg Hakanen, director of Last Wednesday, Associate asset management and real Vice President for News and By JOHN MINSER estate development for Information Don Wycliff told News Writer Notre Dame, said the the South Bend Tribune Unfversity has selected there were some "stumbling The Shirt, in normal years Indianapolis-based develop blocks," but said the as much a staple of Notre er Kite Realty Group for University hopes to strike a Dame football as tailgates and "exclusive negotiations" in deal with Kite. the Victory March, will flood the Eddy Street Commons Wycliff told The Observer the Stadium this season as project. Tuesday he could not dis sales skyrocket far beyond the "It's not for certain [the cuss specifically what need- norm. University is working with "[This year's Shirt] is trend see COMMONS/page 4 ing better than any Shirt we've sold so far," said Sally Wiatrowski, director of retails operations at the Bookstore. -
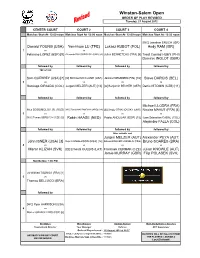
Winston-Salem Open ORDER of PLAY REVISED Tuesday, 21 August 2012
Winston-Salem Open ORDER OF PLAY REVISED Tuesday, 21 August 2012 CENTER COURT COURT 2 COURT 3 COURT 4 Matches Start At: 12:00 noon Matches Start At: 12:00 noon Matches Start At: 12:00 noon Matches Start At: 12:00 noon [WC] Jonathan ERLICH (ISR) Donald YOUNG (USA) Yen-Hsun LU (TPE) Lukasz KUBOT (POL) Andy RAM (ISR) 1 vs vs vs vs Feliciano LOPEZ (ESP) [9] Alexandr DOLGOPOLOV (UKR) [4] Julien BENNETEAU (FRA) [8] Treat Conrad HUEY (PHI) Dominic INGLOT (GBR) followed by followed by followed by followed by TBF 6/3 0/0 Sam QUERREY (USA) [7] [Q] Michael MCCLUNE (USA) Jarkko NIEMINEN (FIN) [16] Steve DARCIS (BEL) 2 vs vs vs vs Santiago GIRALDO (COL) Jurgen MELZER (AUT) [13] [Q] Benjamin BECKER (GER) Denis ISTOMIN (UZB) [11] followed by followed by followed by followed by Michael LLODRA (FRA) Alex BOGOMOLOV JR. (RUS) [WC] David NALBANDIAN (ARG) [14] [Q] Sergiy STAKHOVSKY (UKR) Nicolas MAHUT (FRA) [4] 3 vs vs vs vs [WC] Tomas BERDYCH (CZE) [2] Robin HAASE (NED) Pablo ANDUJAR (ESP) [15] Juan Sebastian CABAL (COL) Alejandro FALLA (COL) followed by followed by followed by followed by After suitable rest Jurgen MELZER (AUT) Alexander PEYA (AUT) John ISNER (USA) [3] Kevin ANDERSON (RSA) [12] Edouard ROGER-VASSELIN (FRA) Bruno SOARES (BRA) 4 vs vs vs vs Martin KLIZAN (SVK) [Q] Ernests GULBIS (LAT) Frantisek CERMAK (CZE) Julian KNOWLE (AUT) Jamie MURRAY (GBR) Filip POLASEK (SVK) Not Before 7:00 PM Jo-Wilfried TSONGA (FRA) [1] 5 vs Thomaz BELLUCCI (BRA) followed by [WC] Ryan HARRISON (USA) 6 vs Marcel GRANOLLERS (ESP) [6] Bill Oakes Miro Bratoev Damian Steiner Mark Darby/Carlos Sanches Tournament Director Tour Manager Referee ATP Supervisor Order of Play released : 20 August 2012 at 22:27 Singles Lucky-Loser Sign-in Deadline : 11:30am MATCHES WILL BE CALLED FROM ANY MATCH ON ANY COURT Doubles Alternate Sign-in Deadline : 11:30am THE PLAYERS' LOUNGE & MAY BE MOVED LOCKER-ROOM. -

Day 2 First-Round Matches Abierto Mexicano
ABIERTO MEXICANO LOS CABOS: DAY 2 MEDIA NOTES Tuesday, August 9, 2016 Cabo del Mar, Cabo San Lucas, Mexico | August 8-13, 2016 Draw: S-28, D-16 | Prize Money: $721,030 | Surface: Outdoor Hard ATP World Tour Info Tournament Info ATP PR & Marketing www.ATPWorldTour.com www.AbiertoLosCabos.com Joshua Rey: [email protected] Twitter: @ATPWorldTour Twitter: @AbiertoLosCabos Press Room: +52-624-688-5676 Facebook: @ATPWorldTour Facebook: @AbiertoLosCabos AFTER MONDAY RAIN, TUESDAY FEATURES ALL 12 1R MATCHES After play was canceled Monday due to rain, the inaugural Abierto Mexicano Los Cabos begins Tuesday with all 12 first-round matches. No. 7 seed Nicolas Almagro and No. 8 seed Marcel Granollers will take action on Stadium. Granollers and his opponent, countryman Fernando Verdasco, are separated by only one spot in the Emirates ATP Rankings. Verdasco climbed two places to pass the Granollers and reach No. 46 after the seedings were already made. Almagro, also from Spain, is now ranked two spots behind Verdasco and one behind Granollers as the World No. 48. He meets American qualifier Noah Rubin. Mexican wild cards Tigre Hank and Lucas Gomez are each seeking the first ATP World Tour victory of their respective careers. Hank, 24, and Gomez, 20, are both 1-7 in tour-level matches, with their lone wins coming in Davis Cup play. Hank faces Austin Krajicek on Stadium, while Gomez goes up against Guillermo-Garcia Lopez on Grandstand. Play begins on Grandstand with No. 6 seed Jeremy Chardy taking on Spanish wild card Pablo Carreño Busta, followed by No. 5 seed Alexandr Dolgopolov meeting Horacio Zeballos. -

Atp Announces New Player Council
News Release 23 June 2012 ATP ANNOUNCES NEW PLAYER COUNCIL LONDON — The new ATP Player Council, selected by ATP player members, was announced at the pre- Wimbledon player meeting this evening. The new ATP Player Council includes returning players Roger Federer, Jarkko Nieminen, Eric Butorac and Andre Sa (served 2002-2004), as well as a number of new faces, elected for a two-year term to represent the ATP player membership. Members elected by their peers to serve on the ATP Player Council through June 2014 are: 1-50 Singles: Kevin Anderson, Roger Federer, Jarkko Nieminen, Gilles Simon 51-100 Singles: Robin Haase, Sergiy Stakhovsky 1-100 Doubles: Mahesh Bhupathi, Eric Butorac At-Large: James Cerretani, Andre Sa Alumni: Brian Gottfried Coach: Claudio Pistolesi (also served 2010-12) ATP Executive Chairman and President Brad Drewett said, “I’d like to congratulate the newly-elected ATP Player Council and thank those players who have concluded their terms. The ATP Player Council plays an incredibly important role in the governance of the ATP, with a seat at the table all year round, helping to make decisions that affect the operation of the ATP World Tour. The players who serve give a significant amount of their personal time, more than people may realise. The men’s game is driving the unprecedented popularity and commercial success of the sport today, and I believe the opportunities ahead of us are very exciting.” The new ATP Player Council will have its first meeting in New York prior to the US Open, where the President and Vice President will be elected. -

Open 13 Provence: 24 February Media Notes
OPEN 13 PROVENCE: 24 FEBRUARY MEDIA NOTES Palais des Sports | Marseille, France | 18-24 February 2019 Draw: S-28, D-16 | Prize Money: €668,485 | Surface: Indoor Hard ATP Tour Tournament Media ATPTour.com Open13.fr Fabienne Benoit: [email protected] (ATP PR) Twitter: @ATP_Tour @Open13 Eli Weinstein: [email protected] (Media Desk) Facebook: @ATPTour @Open13 TV & Radio: TennisTV.com SINGLES AND DOUBLES FINALS [1] Stefanos Tsitsipas (GRE) vs Mikhail Kukushkin (KAZ) Tsitsipas Leads 1-0 18 Dubai (U.A.E.) Hard R32 Stefanos Tsitsipas 6-2 6-7(5) 6-3 Other meeting: 18 ATP Masters 1000 Rome Q (Italy) Clay Q1 Stefanos Tsitsipas 5-7 6-3 7-6(5) Tsitsipas 2019 Summary | 20 years old | World No. 12 (Career High) | 1 Career Title | 10-4 in 2019 | 3-2 at Marseille • Tournament note: Leads the tournament in 28 of 29 service games won. Reached F with straight-sets wins over Hurkacz, Stakhovsky, and Goffin. • Saved 12/12 BPs vs. No. 3 Federer to equal biggest win of career en route to Australian Open SF (l. to Nadal). • Became youngest Grand Slam semi-finalist at age 20 since Djokovic, 20, at 2007 US Open. • Also became youngest Australian Open semi-finalist since Roddick, 20, in 2003. • Made history as 1st Greek to reach Grand Slam QF and SF in men’s singles. • Achieved career-high No. 12 in ATP Rankings on 28 January. Top Greek in ATP Rankings history (since 1973). • Advanced to Sydney QF as No. 1 seed (l. to eventual finalist Seppi). Kukushkin 2019 Summary | 31 years old | World No. -

Tournament Notes
TournamenT noTes as of march 30, 2011 2011 ST. VINCENT TOUR DE PAUL TENNIS TOURNAMENT LITTLE ROCK, AR • APRIL 2–10 USTA PRO CIRCUIT RETURNS TO LITTLE ROCK AS LONGEST-RUNNING MEN’S EVENT TournamenT InFormaTIon The 2011 St. Vincent Tour de Paul Tennis Tournament enters its 31st year on the USTA Site: Pleasant Valley Country Club – Little Rock, Ark. Pro Circuit; the tournament is the longest running event on the USTA Pro Circuit. It is Websites: www.newoutlooktennis.com Susan Mullane the only $15,000 Futures tournament held procircuit.usta.com in Arkansas and concludes the USTA Pro Facebook: St. Vincent Auxiliary New Outlook Circuit spring hard court season, as the clay Tennis Tournament season will begin soon to prepare players for the 2011 French Open. Qualifying Draw Begins: Saturday, April 2 Main Draw Begins: Tuesday, April 5 Former college standouts expected in the main draw include: former University of Main Draw: 32 Singles / 16 Doubles Arkansas All-American Blake Strode, who Surface: Hard / Outdoor won the 2010 US Open National Playoffs to earn a wild card into the 2010 US Open Prize Money: $15,000 Qualifying Tournament, where he won his Former University of Arkansas standout and Tournament Director: first match, and who in 2009 chose to defer 2010 US Open National Playoffs champion Blake Strode deferred Harvard Law School to Breda Turner, (501) 552-3552 Harvard Law School to play professional play pro tennis. [email protected] tennis; former University of North Carolina All-American Nicholas Monroe, who won Tournament Press Contact: his first USTA Pro Circuit singles title since Breda Turner, (501) 552-3552 2007 at the $15,000 Futures in McAllen, the $15,000 Futures in Austin, Texas, [email protected] Texas, last month; and former University of and who has trained at the Roddick-Moros Mississippi All-American Robbye Poole, who International Tennis Academy in San Antonio. -

ERSTE BANK OPEN: DAY 3 MEDIA NOTES Wednesday, October 21, 2015
ERSTE BANK OPEN: DAY 3 MEDIA NOTES Wednesday, October 21, 2015 Wiener Stadthalle, Vienna, Austria | October 19-25, 2015 Draw: S-32, D-16 | Prize Money: €1,745,040 | Surface: Indoor Hard ATP Info: Tournament Info: ATP PR & Marketing: www.ATPWorldTour.com www.erstebank-open.com Martin Dagahs: [email protected] @ATPWorldTour facebook.com/ErsteBankOpenVienna Fabienne Benoit: [email protected] facebook.com/ATPWorldTour Press Room: +43 1 98100578 PAST CHAMPIONS TSONGA, HAAS GO HEAD-TO-HEAD ON WEDNESDAY DAY 3 PREVIEW: The first round concludes and second round begins at the Erste Bank Open on Wednesday. Seeking berths in the quarter-finals are 6-foot-11 Ivo Karlovic and 6-foot-10 John Isner, who will bring their big serves against Sergiy Stakhovsky and Ernests Gulbis respectively. While Karlovic and Isner already have a victory in Vienna this week, No. 2 seed Kevin Anderson and No. 4 seed Jo-Wilfried Tsonga play their opening-round matches on Centre Court. Anderson broke into the Top 10 on Oct. 12, then went on to reach the ATP Masters 1000 Shanghai quarter- finals. But Tsonga defeated him en route to the final and replaced him in this week’s Top 10. On Wednesday, Anderson meets 2010 finalist Andreas Haider-Maurer and Tsonga takes on Tommy Haas in a battle of former champions. Tsonga won the Vienna title in 2011, while Haas captured the championship in 2001 and 2013. Neither player competed at the 2014 Erste Bank Open. FORMER VIENNA FINALISTS IN 2015 DRAW Player Year Final Result David Ferrer* 2014 l. to Murray 57 62 75 Tommy Haas 2013 d.