Accelerator Mass Spectrometry (AMS) Applied in the Measurement of 93Zr
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Production of Radionuclides
CHAPTER 15 Production of Radionuclides Contents 15.1. General considerations 389 15.2. Irradiation yields 390 15.3. Second-order reactions 393 15.4. Target considerations 397 15.4.1. Physical properties 397 15.4.2. Chemical properties 398 15.5. Product specifications 399 15.5.1. Radiochemical processing 399 15.5.2. Specific activity 400 15.5.3. Labeling 400 15.5.4. Radiochemical purity 401 15.6. Recoil separations 402 15.6.1. Target recoil products 402 15.6.2. Hot atom reactions 403 15.6.3. The Szilard-Chalmers process 404 15.7. Fast radiochemical separations 406 15.7.1. Production of 11C labeled compounds 407 15.7.2. Auto-batch procedures 407 15.7.3. On-line procedures: gas-phase separation 409 15.7.4. On-line procedures: solvent extraction 412 15.7.5. Mass separator procedures 412 15.8. Exercises 412 15.9. Literature 414 This chapter discusses production of radionuclides for beneficial use in science, medicine and technology. The nuclear fundamentals for the production processes have been given in Chapters 11 to 14. The formation of radionuclides is discussed in several Chapters: e.g. cosmogenic reactions leading to the formation of short-lived radionuclides in nature (Ch. 5 and 10); thermonuclear reactions leading to the formation of long-lived radioactivity in the universe (Ch. 17); the synthesis of trans-uranium elements (Ch. 16 and 19-21). The production and isolation of separated fission products is treated separately (Ch. 19-21). This chapter discusses aspects of fundamental importance to the production of radionuclides by a variety of methods. -

Lawrence Berkeley National Laboratory Recent Work
Lawrence Berkeley National Laboratory Recent Work Title RADIOCHEMICAL AND SPECTROMETER STUDIES OF SEVERAL NEUTRON-DEFICIENT ZIRCONIUM ISOTOPES AND THEIR DECAY PRODUCTS Permalink https://escholarship.org/uc/item/5ck8q7xw Authors Hyde, Earl K. O'Kelley, Grover D. Publication Date 1950-12-28 eScholarship.org Powered by the California Digital Library University of California UCRL- .Jt)AJ,-.64.. _.; >-w .J w ... ~ ,• 0:: w m I . ;•· <( z 0:: 0 LL ..J u<( LL 0 >- 1-- TWO-WEEK LOAN COPY (/) This is a Library Circulating Copy 0:: which may be borrowed for two weeks. w For a personal retention copy, call > Tech. Info. Diuision, Ext. 5545 z '.-o:-. :J ~~ RADIATION LABORATORY DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any · information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California. -

Technische Universität München Physik-Department Study of The
Technische Universität München Physik-Department Study of the biokinetics of zirconium isotopes in humans and its relevance to internal dosimetry Matthias Greiter Vollständiger Abdruck der von der Fakultät für Physik der Technischen Universität München zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften genehmigten Dissertation. Vorsitzender: Univ.-Prof. Dr. J. L. van Hemmen Prüfer der Dissertation: 1. Hon.-Prof. Dr. H.G. Paretzke 2. Univ.-Prof. Dr. F. von Feilitzsch Die Dissertation wurde am 27.09.2007 bei der Technischen Universität München eingereicht und durch die Fakultät für Physik am 22.04.2008 angenommen. i Author contact information: Matthias Greiter Institute of Radiation Protection Helmholtz Zentrum München German Research Center for Environmental Health (GmbH) Ingolstaedter Landstrasse 1 85764 Neuherberg Germany E-mail: [email protected] ii Table of contents Abstract ...................................................................................................................................... 1 List of acronyms, symbols and abbreviations ............................................................................ 2 1 Aim of the study......................................................................................................... 3 1.1 Natural occurrence of zirconium compounds ............................................................ 3 1.2 Applications of stable zirconium................................................................................ 5 1.3 Applications -

Development of a National Neutron Database for Nuclear Technology
- 7 - XA9744992 DEVELOPMENT OF A NATIONAL NEUTRON DATABASE FOR NUCLEAR TECHNOLOGY A. V. Ignatyuk, V.N. Kononov, B.D. Kuzminov, V.N. Manokhin M.N. Nikolaev, B.I. Furzov State Research Centre of the Russian Federation Institute of Physics and Power Engineering, Obninsk Abstract This paper describes the stages of a many years activities at the IPPE consisting of the measurement, theoretical description and evaluation of neutron data, and of the establishment of a national data bank of neutron data for nuclear technology. A list of libraries which are stored at the Nuclear Data Centre is given. Introduction Currently, nuclear technology has found wide applications in a number of fields in science and technology consisting of: - nuclear energy (nuclear fission reactors, nuclear fission reactors, radioisotopic sources) - nuclear transmutation (production of radioisotopes for medical and other applications, burn-up of long-lived radio nuclides, radiation alloying of semiconducting materials, etc..) - nuclear instrumentation in industry (activation analysis, nuclear micro-analysis, control of fissile materials, etc..) - scientific investigations (nuclear physics, nuclear astrophysics, medicine, radiobiology, agro-radiology, ecology, etc.). In the sphere of nuclear technology, a number of processes use more than 500 stable and radioactive nuclides in a broad energy range. To ascertain the proper functioning of nuclear installations which have various functions and applications in industrial projects and scientific investigations, there is a need for nuclear data that characterize the properties of nuclear reactions. The reliability of radiation and nuclear safety, the ecological acceptance, and the economical planning of nuclear installations, all depend on the completeness, quality and accuracy of nuclear data. -
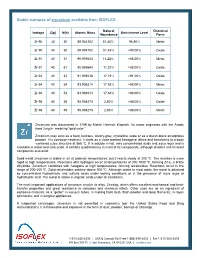
Stable Isotopes of Zirconium Available from ISOFLEX
Stable isotopes of zirconium available from ISOFLEX Natural Chemical Isotope Z(p) N(n) Atomic Mass Enrichment Level Abundance Form Zr-90 40 50 89.904702 51.45% 96.80% Metal Zr-90 40 50 89.904702 51.45% >98.00% Oxide Zr-91 40 51 90.905643 11.22% >88.00% Metal Zr-91 40 51 90.905643 11.22% >88.00% Oxide Zr-92 40 52 91.905038 17.15% >91.00% Oxide Zr-94 40 54 93.906314 17.38% >98.00% Metal Zr-94 40 54 93.906314 17.38% >98.00% Oxide Zr-96 40 56 95.908275 2.80% >86.00% Oxide Zr-96 40 56 95.908275 2.80% >86.00% Metal Zirconium was discovered in 1789 by Martin Heinrich Klaproth. Its name originates with the Arabic word zargun, meaning “gold color.” Zirconium may exist as a hard, lustrous, silvery-gray, crystalline scale or as a bluish-black amorphous powder. It is corrosion-resistant. It starts as a close-packed hexagonal lattice and transforms to a body -centered cubic structure at 865 ºC. It is soluble in hot, very concentrated acids and aqua regia and is insoluble in water and cold acids. It exhibits quadrivalency in most of its compounds, although divalent and trivalent compounds also exist. Solid metal zirconium is stable in air at ordinary temperatures, but it reacts slowly at 200 ºC. The reaction is more rapid at high temperatures. Reactions with hydrogen occur at temperatures of 300-1000 ºC, forming ZrH2, a brittle dihydride. Zirconium combines with halogens at high temperatures, forming tetrahalides. -

Theoretical Potential of the CANDU Core for Transmutation of PWR TRU Nuclides
Proceedings of the Reactor Physics Asia 2015 (RPHA15) Conference Jeju, Korea, Sept. 16-18, 2015 Theoretical Potential of the CANDU Core for Transmutation of PWR TRU Nuclides Jinqi Lyu, Donny Hartanto, Mohammad Abdul Motalab and Yonghee Kim Department of Nuclear and Quantum Engineering, KAIST 291 Daehak-ro, Yusong-gu, Daejeon 34141, Republic of Korea *Corresponding author: [email protected] 1. Introduction 2. Analysis Models and Methods Transuranic (TRU) nuclides generated in spent fuels In this work, the analysis is done only for a 2-D fuel from the Light Water Reactor (LWR) pose a big assembly lattice because the core characteristics can be challenge in nuclear waste management due to its well determined through lattice analyses in CANDU potential diversion, high radiological toxicity and long core. The lattice calculation is performed for a lifetime. One of the potential approaches for dealing CANFLEX fuel bundle, as illustrated in Fig. 1, which with spent nuclear fuel is to fully utilize (transmute) the can improve the operating and safety margin, as well as TRU nuclides in nuclear reactors as nuclear fuels. the economics of a CANDU reactor. There have been many studies about utilizing TRU nuclides in CANDU reactors since many design features of CANDU reactor make it uniquely suitable for transmuting TRU nuclides, such as simple fabrication and handling of active fuels, precise management of core reactivity, high neutron economy and so on [1]. The concept of MOX (mixed oxides) fuel, which mixes actinides with natural uranium, and IMF (inert matrix fuel), which mixes actinides with silicon carbide, were proposed previously. -

Publication List Prof. Dr. Norbert Trautmann (Aug
Publication List Prof. Dr. Norbert Trautmann (Aug. 2012) R. Denig, N. Trautmann, G. Herrmann Schnelle Extraktion durch quasi-feste Extraktionsmittel Z. Analyt. Chem. 216, 41 (1966) N. Trautmann, R. Denig, N. Kaffrell, G. Herrmann Heavy Isotopes of Protactinium Z. Naturforsch. 23a, 2127 (1968) N. Trautmann, R. Denig, G. Herrmann Wirkungsquerschnitte der (n,p)-, (n,pn)- und (n,α)-Reaktionen am Uran-238 mit 15-MeV- Neutronen und Nachweis des Thoriums-235 Radiochim. Acta 11, 168 (1969) R. Denig, N. Trautmann, G. Herrmann Trennung von Spaltprodukten durch Extraktionschromatographie I. Bestimmung der Verteilungskoeffizienten J. Radioanal. Chem. 5, 223 (1970) R. Denig, N. Trautmann, G. Herrmann Trennung von Spaltprodukten durch Extraktionschromatographie II. Trennung von Mutter-Tochter-Paaren J. Radioanal. Chem. 6, 57 (1970) R. Denig, N. Trautmann, G. Herrmann Trennung von Spaltprodukten durch Extraktionschromatographie III. Auftrennung eines Spaltproduktgemisches J. Radioanal. Chem. 6, 331 (1970) G. Herrmann, N. Kaffrell, N. Trautmann, R. Denig, W. Herzog, D. Hübscher, K.-L. Kratz Some Studies on Neutron-Rich Nuclei CERN 70-30, 2, 985 (1970) International Conference on the Properties of Nuclei far from the Region of Beta-Stability, Leysin, Sept. 1970 M. Weber, N. Trautmann, G. Herrmann Volatilization of Fission Products from Solid Uranium Tetrafluoride Radiochem. Radioanal. Lett. 6, 73 (1971) R. Denig, N. Trautmann, N. Kaffrell, G. Herrmann Heavy Isotopes of Protactinium: Formation, Isolation, Mass Assignment and Cross Sections BMBW-FB K 71-17, 2-1 (1971) Tagungsbericht der 3. Internationalen Protaktiniumkonferenz, Schloβ Elmau bei Mittenwald, April 1969 N. Trautmann, N. Kaffrell, R. Denig, G. Herrmann Schwere Isotope des Protactiniums: Zerfall des 9.1 min 236Pa und 8.7 min 237Pa BMBW-FB K 71-17, 3-1 (1971) Tagungsbericht der 3. -
UNCLASSIFIED a *.** 9
-.” . APPROVED FOR PULBIC RELEASE a UNCLASSIFIED 9: ● *.** ● ● ●:0: ●:0:.e●9** . LIA-Z1Q3L CW14 REP*T GOUHION Copy No. a, ~ 6?EPRODLICTION Cig COPY AECRESEARCHANDDEVELOPMENTREPORT LOS ALAMOS SCIENTIFIC LABORATORY OF THE UNIVERSITYOF CALIFORNIAo LOSALAMOS NEW MEXICO PYROMETALLURGY EXPERIMENTS ON PLUTONIUM-RICH REACTOR FUELS (Project Status Report as of March 31, 195’7) UNCLASSIFIED ,- -. .--— .-—. ——-—. ----- . -.. —.-, -- m –—e= = .–— =-– ..=– -—=- -. ..~. r .- ~.——.- .-- .-. -------.. -.—--—.-— ------ -.--- —.. ..— .—— — -.=— ... --.=. .- ..__ .:. -.. .. ... —_*~08e 6.*. -*. .? ● — ._ -:. —. _-. — .. .._ ___ .=. -——— -—-_ —__ - —.-—. — . —----- .. -.-— --——= .— - APPROVED● e FOR PUBLIC RELEASE .. APPROVED FOR PULBIC RELEASE . ● e ● 00 ● 00 ● e* ● 9* be ‘ ● .00: : .:0. ● m ● *m ● m : : : :0 ● * ●0: ● 90 ● ● 00 ● LEGAL NOTICE This report was prepared as an account of Govern- ment sponsored work, Neither the United States, nor the Commission, nor any person acting on behalf of the Com- mission: A. Makes Wy warraqty or representation, express or implied, with respect to the accuracy, completeness, or Usefqlne>s of the information contained in this report, or that tfie U$e ,“oj’ any information, apparatus, method, or process disclosed’ in this report may not infringe privately owned ,rights; or B. Assure-es any liabilities with respect to the use of, or for dam ages,, resulting from the use of any infor- m ation, appar&s, method, or process disclosed in this report. AS used intheabove,‘personacting on behalf of the Commission “ includes any employee or contractor of the Commission to the extent that such employee or contrac- tor prepares, handles or distributes, or provides access to, any information pursuant to his employment or con- tract with the Commission.. Printed in USA. Charge 35 cents. Available from the U. S. Atomic Energy Commission, Technical Information Service Extension, P. -

United States Patent (19) 11 Patent Number: 4,721,596 Marriott Et Al
United States Patent (19) 11 Patent Number: 4,721,596 Marriott et al. (45) Date of Patent: Jan. 26, 1988 54 METHOD FOR NET DECREASE OF New Scientist, 7/77, pp. 14-16, Steinberg. HAZARDOUS RADIOACTIVE NUCLEAR CONF-760622-3, "Actinide Transmutation Studies: A WASTE MATERALS Review”, Croff, 6/76, pp. 1-14. (75) Inventors: Richard Marriott, Detroit, Mich.; BNWL-1900 (vol. 1), 5/74, Schreider et al., pp. Frank S. Henyey, San Diego; Adolf 1.42-1.45, 1.67. R. Hochstim, La Jolla, both of Calif. Huse et al., "Fusion-Fission Energy Systems: Some Utility Perspectives', ERDA-4, Dec. 3, 1974, pp. 73 Assignee: Perm, Inc., La Jolla, Calif. 27-61. (21) Appl. No.: 613,013 Tenney, “A Tokamak Hybrid Study," CONF-760733, pp. 71-80. 22 Filed: May 22, 1984 Rose et al, "Tokamak Antinide Burner Design Study', US-USSR Symposium of Fusion-Fission Reactors, Jul. Related U.S. Application Data 13-16, 1976, pp. 91-115. 63 Continuation of Ser. No. 455,046, Jan. 3, 1983, aban 'Alternatives for Managing Wastes From Reactors and doned, which is a continuation of Ser. No. 100,658, Post-Fission Operations in the LWRFuel Cycle', ER Dec. 5, 1979, abandoned. DA-76-43, vol. 4. 51) Int. Cl." .......................... G21G 1/02; G21G 1/06 "A Radioisotope-Oriented View of Nuclear Waste 52 U.S. Cl. .................................... 376/189; 376/169; Management', A. F. Rupp, ORNL-4476 (1972). 376/170; 376/184; 376/186; 376/158 "A Re-Examination of the Permanent Disposal of Ra 58) Field of Search ............... 376/184, 189, 158, 170, dioactive Waste', Marriott et al RIES 75-106 (1975). -

Determination of Zirconium Isotope Composition and Concentration For
Determination of zirconium isotope composition and concentration for nuclear sample analysis using Thermal Ionization Mass Spectrometry Alexandre Quémet, Christophe Maillard, Alexandre Ruas To cite this version: Alexandre Quémet, Christophe Maillard, Alexandre Ruas. Determination of zirconium isotope compo- sition and concentration for nuclear sample analysis using Thermal Ionization Mass Spectrometry. In- ternational Journal of Mass Spectrometry, Elsevier, 2015, 392, pp.34-40. 10.1016/j.ijms.2015.08.023. cea-02384282 HAL Id: cea-02384282 https://hal-cea.archives-ouvertes.fr/cea-02384282 Submitted on 28 Nov 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Determination of zirconium isotope composition and concentration for nuclear sample analysis using Thermal Ionization Mass Spectrometry Alexandre Quemet*, Christophe Maillard and Alexandre Ruas CEA, Nuclear Energy Division, RadioChemistry & Processes Department, F-30207 Bagnols sur Cèze, France * Corresponding author. E-mail address: [email protected] (A. Quemet) Keywords: TIMS; zirconium; isotope ratio; isotope dilution; separation Abstract: A new Thermal Ionization Mass Spectrometer (TIMS) analytical procedure was developed to measure with high accuracy the zirconium isotope abundance and concentration without molybdenum correction in nuclear samples. A zirconium selective separation using UTEVA column was used before the TIMS measurement in order to remove all possible isobaric interferences (Mo, Y, Nb and Ru) in the solution. -

Vladimir MANEA
UNIVERSITÉ PARIS-SUD ÉCOLE DOCTORALE 517 : PARTICULES, NOYAUX ET COSMOS Laboratoire : CSNSM-IN2P3-CNRS, UMR 8609 THÈSE DE DOCTORAT PHYSIQUE par Vladimir MANEA Penning-trap mass measurements of exotic CERN-THESIS-2014-351 29/09/2014 rubidium and gold isotopes for a mean-field study of pairing and quadrupole correlations Date de soutenance : 29/09/2014 Composition du jury : Directeur de thèse : David LUNNEY Directeur de Recherche CNRS, CSNSM, Orsay, France Rapporteurs : Héloïse GOUTTE Ingénieure Physicienne, CEA/DSM, Centre de Saclay, France Piet VAN DUPPEN Professeur, KU, Leuven, Belgique Examinateurs : Brigitte ROUSSIÈRE Directrice de Recherche CNRS, IPN, Orsay, France Hervé SAVAJOLS Chargé de Recherche CNRS, GANIL, Caen, France Nigel ORR Directeur de Recherche CNRS, LPC, Caen, France Abstract The most complex nuclei are situated between the magic and the mid-shell ones, in regions known for sudden changes of the trends of nuclear observables. These are the so-called shape-transition regions, where the nuclear paradigm changes from the vibrational liquid drop to the static rotor. With few exceptions, nuclei in these regions are radioactive, with half-lives dropping into the millisecond range. Complementing the information obtained from the low-lying excitation spectrum, nu- clear binding energies and mean-square charge radii are among the observables most sensitive to these changes of nuclear structure. In the present work, a study of the shape- transition phenomenon is performed by measurements of radioactive nuclides produced by the ISOLDE facility at CERN. The masses of the neutron-rich rubidium isotopes 98−100Rb and of the neutron-deficient gold isotopes 180;185;188;190;191Au are determined us- ing the Penning-trap mass spectrometer ISOLTRAP. -

Measurement Techniques for Tracer Kinetic Studies with Stable Isotopes of Zirconium M
Radiation Protection Dosimetry (2007), Vol. 127, No. 1–4, pp. 266–269 doi:10.1093/rpd/ncm347 Advance Access publication 17 October 2007 MEASUREMENT TECHNIQUES FOR TRACER KINETIC STUDIES WITH STABLE ISOTOPES OF ZIRCONIUM M. Greiter1,*, K. Abbas2, M. C. Cantone3, W. Carli4, A. Geisler1, U. Gerstmann1, A. Giussani1,3, R. Hertenberger4, U. Holzwarth2, O. Meisenberg1,V.Ho¨llriegl1, U. Oeh1, I. Veronese3 and H. G. Paretzke1 1GSF—National Research Center for Environment and Health, 85764 Neuherberg, Germany 2European Commission JRC, Institute for Health and Consumer Protection, 21020 Ispra (Va), Italy 3Universita` degli Studi di Milano, Dipartimento di Fisica and INFN, Sezione di Milano, 20133 Milano, Italy 4MLL—Maier-Leibnitz Laboratory, 85748 Garching, Germany Downloaded from Biokinetic models are used in radiation protection to assess internal radiation doses. Experiments with stable isotopes as tracers can be performed to obtain characteristic parameters of these models. Two methods for the measurement of zirconium isotopes in human biological samples are presented—thermal ionisation mass spectrometry (TIMS) and proton nuclear acti- vation analysis (PNA). Descriptions include sample preparation, operating conditions, relative uncertainties and method detec- tion limits as well as important properties of both methods. http://rpd.oxfordjournals.org/ INTRODUCTION (2) Any suitable method must be able to measure low amounts of the target substance in human Internal radiation doses are impractical to measure, fluid samples, i.e. 1 ng per sample in the case therefore, biokinetic models are used to assess these of zirconium. In a tracer experiment, the tracer doses. In order to build such models, the distribution concentration should be as low as possible in of radionuclides in the human body must be measured order not to disturb the normal metabolism of directly or estimated from animal experiments and the naturally occurring substance.