Finding Volumes by Integration
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hydraulic Cylinder Replacement for Cylinders with 3/8” Hydraulic Hose Instructions
HYDRAULIC CYLINDER REPLACEMENT FOR CYLINDERS WITH 3/8” HYDRAULIC HOSE INSTRUCTIONS INSTALLATION TOOLS: INCLUDED HARDWARE: • Knife or Scizzors A. (1) Hydraulic Cylinder • 5/8” Wrench B. (1) Zip-Tie • 1/2” Wrench • 1/2” Socket & Ratchet IMPORTANT: Pressure MUST be relieved from hydraulic system before proceeding. PRESSURE RELIEF STEP 1: Lower the Power-Pole Anchor® down so the Everflex™ spike is touching the ground. WARNING: Do not touch spike with bare hands. STEP 2: Manually push the anchor into closed position, relieving pressure. Manually lower anchor back to the ground. REMOVAL STEP 1: Remove the Cylinder Bottom from the Upper U-Channel using a 1/2” socket & wrench. FIG 1 or 2 NOTE: For Blade models, push bottom of cylinder up into U-Channel and slide it forward past the Ram Spacers to remove it. Upper U-Channel Upper U-Channel Cylinder Bottom 1/2” Tools 1/2” Tools Ram 1/2” Tools Spacers Cylinder Bottom If Ram-Spacers fall out Older models have (1) long & (1) during removal, push short Ram Spacer. Ram Spacers 1/2” Tools bushings in to hold MUST be installed on the same side Figure 1 Figure 2 them in place. they were removed. Blade Models Pro/Spn Models Need help? Contact our Customer Service Team at 1 + 813.689.9932 Option 2 HYDRAULIC CYLINDER REPLACEMENT FOR CYLINDERS WITH 3/8” HYDRAULIC HOSE INSTRUCTIONS STEP 2: Remove the Cylinder Top from the Lower U-Channel using a 1/2” socket & wrench. FIG 3 or 4 Lower U-Channel Lower U-Channel 1/2” Tools 1/2” Tools Cylinder Top Cylinder Top Figure 3 Figure 4 Blade Models Pro/SPN Models STEP 3: Disconnect the UP Hose from the Hydraulic Cylinder Fitting by holding the 1/2” Wrench 5/8” Wrench Cylinder Fitting Base with a 1/2” wrench and turning the Hydraulic Hose Fitting Cylinder Fitting counter-clockwise with a 5/8” wrench. -

An Introduction to Topology the Classification Theorem for Surfaces by E
An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5. -

Volumes of Prisms and Cylinders 625
11-4 11-4 Volumes of Prisms and 11-4 Cylinders 1. Plan Objectives What You’ll Learn Check Skills You’ll Need GO for Help Lessons 1-9 and 10-1 1 To find the volume of a prism 2 To find the volume of • To find the volume of a Find the area of each figure. For answers that are not whole numbers, round to prism a cylinder the nearest tenth. • To find the volume of a 2 Examples cylinder 1. a square with side length 7 cm 49 cm 1 Finding Volume of a 2. a circle with diameter 15 in. 176.7 in.2 . And Why Rectangular Prism 3. a circle with radius 10 mm 314.2 mm2 2 Finding Volume of a To estimate the volume of a 4. a rectangle with length 3 ft and width 1 ft 3 ft2 Triangular Prism backpack, as in Example 4 2 3 Finding Volume of a Cylinder 5. a rectangle with base 14 in. and height 11 in. 154 in. 4 Finding Volume of a 6. a triangle with base 11 cm and height 5 cm 27.5 cm2 Composite Figure 7. an equilateral triangle that is 8 in. on each side 27.7 in.2 New Vocabulary • volume • composite space figure Math Background Integral calculus considers the area under a curve, which leads to computation of volumes of 1 Finding Volume of a Prism solids of revolution. Cavalieri’s Principle is a forerunner of ideas formalized by Newton and Leibniz in calculus. Hands-On Activity: Finding Volume Explore the volume of a prism with unit cubes. -
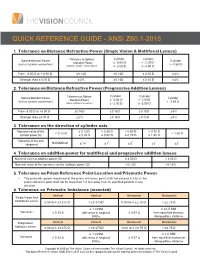
Quick Reference Guide - Ansi Z80.1-2015
QUICK REFERENCE GUIDE - ANSI Z80.1-2015 1. Tolerance on Distance Refractive Power (Single Vision & Multifocal Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -4.50 D (minus cylinder convention) ≤ -2.00 D ≤ -4.50 D From - 6.50 D to + 6.50 D ± 0.13 D ± 0.13 D ± 0.15 D ± 4% Stronger than ± 6.50 D ± 2% ± 0.13 D ± 0.15 D ± 4% 2. Tolerance on Distance Refractive Power (Progressive Addition Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -3.50 D (minus cylinder convention) ≤ -2.00 D ≤ -3.50 D From -8.00 D to +8.00 D ± 0.16 D ± 0.16 D ± 0.18 D ± 5% Stronger than ±8.00 D ± 2% ± 0.16 D ± 0.18 D ± 5% 3. Tolerance on the direction of cylinder axis Nominal value of the ≥ 0.12 D > 0.25 D > 0.50 D > 0.75 D < 0.12 D > 1.50 D cylinder power (D) ≤ 0.25 D ≤ 0.50 D ≤ 0.75 D ≤ 1.50 D Tolerance of the axis Not Defined ° ° ° ° ° (degrees) ± 14 ± 7 ± 5 ± 3 ± 2 4. Tolerance on addition power for multifocal and progressive addition lenses Nominal value of addition power (D) ≤ 4.00 D > 4.00 D Nominal value of the tolerance on the addition power (D) ± 0.12 D ± 0.18 D 5. Tolerance on Prism Reference Point Location and Prismatic Power • The prismatic power measured at the prism reference point shall not exceed 0.33Δ or the prism reference point shall not be more than 1.0 mm away from its specified position in any direction. -

A Three-Dimensional Laguerre Geometry and Its Visualization
A Three-Dimensional Laguerre Geometry and Its Visualization Hans Havlicek and Klaus List, Institut fur¨ Geometrie, TU Wien 3 We describe and visualize the chains of the 3-dimensional chain geometry over the ring R("), " = 0. MSC 2000: 51C05, 53A20. Keywords: chain geometry, Laguerre geometry, affine space, twisted cubic. 1 Introduction The aim of the present paper is to discuss in some detail the Laguerre geometry (cf. [1], [6]) which arises from the 3-dimensional real algebra L := R("), where "3 = 0. This algebra generalizes the algebra of real dual numbers D = R("), where "2 = 0. The Laguerre geometry over D is the geometry on the so-called Blaschke cylinder (Figure 1); the non-degenerate conics on this cylinder are called chains (or cycles, circles). If one generator of the cylinder is removed then the remaining points of the cylinder are in one-one correspon- dence (via a stereographic projection) with the points of the plane of dual numbers, which is an isotropic plane; the chains go over R" to circles and non-isotropic lines. So the point space of the chain geometry over the real dual numbers can be considered as an affine plane with an extra “improper line”. The Laguerre geometry based on L has as point set the projective line P(L) over L. It can be seen as the real affine 3-space on L together with an “improper affine plane”. There is a point model R for this geometry, like the Blaschke cylinder, but it is more compli- cated, and belongs to a 7-dimensional projective space ([6, p. -

Natural Cadmium Is Made up of a Number of Isotopes with Different Abundances: Cd106 (1.25%), Cd110 (12.49%), Cd111 (12.8%), Cd
CLASSROOM Natural cadmium is made up of a number of isotopes with different abundances: Cd106 (1.25%), Cd110 (12.49%), Cd111 (12.8%), Cd 112 (24.13%), Cd113 (12.22%), Cd114(28.73%), Cd116 (7.49%). Of these Cd113 is the main neutron absorber; it has an absorption cross section of 2065 barns for thermal neutrons (a barn is equal to 10–24 sq.cm), and the cross section is a measure of the extent of reaction. When Cd113 absorbs a neutron, it forms Cd114 with a prompt release of γ radiation. There is not much energy release in this reaction. Cd114 can again absorb a neutron to form Cd115, but the cross section for this reaction is very small. Cd115 is a β-emitter C V Sundaram, National (with a half-life of 53hrs) and gets transformed to Indium-115 Institute of Advanced Studies, Indian Institute of Science which is a stable isotope. In none of these cases is there any large Campus, Bangalore 560 012, release of energy, nor is there any release of fresh neutrons to India. propagate any chain reaction. Vishwambhar Pati The Möbius Strip Indian Statistical Institute Bangalore 560059, India The Möbius strip is easy enough to construct. Just take a strip of paper and glue its ends after giving it a twist, as shown in Figure 1a. As you might have gathered from popular accounts, this surface, which we shall call M, has no inside or outside. If you started painting one “side” red and the other “side” blue, you would come to a point where blue and red bump into each other. -

10-4 Surface and Lateral Area of Prism and Cylinders.Pdf
Aim: How do we evaluate and solve problems involving surface area of prisms an cylinders? Objective: Learn and apply the formula for the surface area of a prism. Learn and apply the formula for the surface area of a cylinder. Vocabulary: lateral face, lateral edge, right prism, oblique prism, altitude, surface area, lateral surface, axis of a cylinder, right cylinder, oblique cylinder. Prisms and cylinders have 2 congruent parallel bases. A lateral face is not a base. The edges of the base are called base edges. A lateral edge is not an edge of a base. The lateral faces of a right prism are all rectangles. An oblique prism has at least one nonrectangular lateral face. An altitude of a prism or cylinder is a perpendicular segment joining the planes of the bases. The height of a three-dimensional figure is the length of an altitude. Surface area is the total area of all faces and curved surfaces of a three-dimensional figure. The lateral area of a prism is the sum of the areas of the lateral faces. Holt Geometry The net of a right prism can be drawn so that the lateral faces form a rectangle with the same height as the prism. The base of the rectangle is equal to the perimeter of the base of the prism. The surface area of a right rectangular prism with length ℓ, width w, and height h can be written as S = 2ℓw + 2wh + 2ℓh. The surface area formula is only true for right prisms. To find the surface area of an oblique prism, add the areas of the faces. -

Plus Cylinder Lensometry Tara L Bragg, CO August 2015
Mark E Wilkinson, OD Plus Cylinder Lensometry Tara L Bragg, CO August 2015 Lensometry A lensometer is an optical bench consisting of an illuminated moveable target, a powerful fixed lens, and a telescopic eyepiece focused at infinity. The key element is the field lens that is fixed in place so that its focal point is on the back surface of the lens being analyzed. The lensometer measures the back vertex power of the spectacle lens. The vertex power is the reciprocal of the distance between the back surface of the lens and its secondary focal point. This is also known as the back focal length. For this reason, a lensometer does not really measure the true focal length of a lens, which is measured from the principal planes, not from the lens surface. The lensometer works on the Badal principle with the addition of an astronomical telescope for precise detection of parallel rays at neutralization. The Badel principle is Knapp’s law applied to lensometers. Performing Manual Lensometry Focusing the Eyepiece The focus of the lensometer eyepiece must be verified each time the instrument is used, to avoid erroneous readings. 1. With no lens or a plano lens in place on the lensometer, look through the eyepiece of the instrument. Turn the power drum until the mires (the perpendicular cross lines), viewed through the eyepiece, are grossly out of focus. 2. Turn the eyepiece in the plus direction to fog (blur) the target seen through the eyepiece. 3. Slowly turn the eyepiece in the opposite direction until the target is clear, then stop turning. -

Tadpole Cancellation in Unoriented Liouville Theory
UT-03-29 hep-th/0309063 September, 2003 Tadpole Cancellation in Unoriented Liouville Theory Yu Nakayama1 Department of Physics, Faculty of Science, University of Tokyo Hongo 7-3-1, Bunkyo-ku, Tokyo 113-0033, Japan Abstract The tadpole cancellation in the unoriented Liouville theory is discussed. Using two different methods — the free field method and the boundary-crosscap state method, we derive one-loop divergences. Both methods require two D1-branes with the symplectic gauge group to cancel the orientifold tadpole divergence. However, the finite part left is different in each method and this difference is studied. We also discuss the validity of the free field method and the possible applications of our result. arXiv:hep-th/0309063v4 20 Nov 2003 1E-mail: [email protected] 1 Introduction The matrix-Liouville correspondence is one of the simplest examples of the open-closed duality2. The new interpretation of the matrix model [5][6][7][8] is that we regard this matrix quantum mechanics as the effective dynamics of the open tachyon filed which lives on D0-branes stacked at the boundary of the Liouville direction φ [9]. →∞ Extending this idea to the unoriented Liouville theory (or with an orientifold plane) is interesting, since we less understand the open-closed duality with an orientifold plane than the case without one. However, it is well-known that unoriented theories usually have tadpoles when the space-filling orientifold plane is introduced. Since the appearance of tadpoles implies divergences in many amplitudes (usually referred to as an internal inconsistency), it must be cancelled somehow. -
Lesson 10: Volumes of Familiar Solids―Cones and Cylinders
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 10 8•5 Lesson 10: Volumes of Familiar Solids―Cones and Cylinders Student Outcomes . Students know the volume formulas for cones and cylinders. Students apply the formulas for volume to real-world and mathematical problems. Lesson Notes For the demonstrations in this lesson, the following items are needed: a stack of same-sized note cards, a stack of same- sized round disks, a cylinder and cone of the same dimensions, and something with which to fill the cone (e.g., rice, sand, or water). Demonstrate to students that the volume of a rectangular prism is like finding the sum of the areas of congruent rectangles, stacked one on top of the next. A similar demonstration is useful for the volume of a cylinder. To demonstrate that the volume of a cone is one-third that of the volume of a cylinder with the same dimension, fill a cone with rice, sand, or water, and show students that it takes exactly three cones to equal the volume of the cylinder. Classwork Opening Exercise (3 minutes) Students complete the Opening Exercise independently. Revisit the Opening Exercise once the discussion below is finished. Opening Exercise a. i. Write an equation to determine the volume of the rectangular prism shown below. MP.1 & MP.7 푽 = ퟖ(ퟔ)(풉) = ퟒퟖ풉 The volume is ퟒퟖ풉 퐦퐦ퟑ. Lesson 10: Volumes of Familiar Solids―Cones and Cylinders 130 This work is derived from Eureka Math ™ and licensed by Great Minds. ©2015 Great Minds. eureka-math.org This work is licensed under a This file derived from G8-M5-TE-1.3.0-10.2015 Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. -

Geometry Module 3 Lesson 6 General Prisms and Cylinders and Their Cross-Sections
GEOMETRY MODULE 3 LESSON 6 GENERAL PRISMS AND CYLINDERS AND THEIR CROSS-SECTIONS OPENING EXERCISE Complete the opening exercise on page 39 in your workbook. Include the hidden edges. Is a right rectangular prism hollow? That is, does it include the points inside? DISCUSSION Right Rectangular Prism: Let E and 퐸’ be two parallel planes.1 Let B be a rectangular region* in the plane E.2 At each point P of B, consider the 푃푃̅̅̅̅̅′ perpendicular to E, joining P to a point 푃′ of the plane 퐸’.3 The union of all these segments is called a right rectangular prism.4 * A rectangular region is the union of a rectangle and its interior. Definition Review Lateral Edge Lateral Face Base General Cylinder: Let E and 퐸’ be two parallel planes, let B be a region* in the plane E, and let L be a line that intersects E and 퐸’ but not B. At each point P of B, consider 푃푃̅̅̅̅̅′ parallel to L, joining P to a point 푃′ of the plane 퐸’. The union of all these segments is called a general cylinder with base B. * A region refers to a polygonal region (triangle, quadrilateral, pentagon, and hexagon), a circular region or regions that can be decomposed into such regions. MOD3 L6 1 Compare the definitions of right rectangular prism and general cylinder. How are they different? The definitions are similar. However, in the right rectangular prism, the region B is a rectangular region. In a general cylinder, the shape of B is not specified. Also, the segments (푃푃̅̅̅̅̅′) in the right rectangular prism must be perpendicular. -

The Shape of a Möbius Strip
The shape of a M¨obius strip E.L. Starostin1, G.H.M. van der Heijden1 The M¨obius strip, obtained by taking a rectangular strip of plastic or paper, twisting one end through 180◦, and then joining the ends, is the canonical example of a one-sided surface. Finding its character- istic developable shape has been an open problem ever since its first formulation in [22, 23]. Here we use the invariant variational bicomplex formalism to derive the first equilibrium equations for a wide developable strip undergoing large deformations, thereby giving the first non-trivial demonstration of the potential of this approach. We then formulate the boundary-value problem for the M¨obius strip and solve it numerically. Solutions for increasing width show the formation of creases bounding nearly flat triangular regions, a feature also familiar from fabric draping [6] and paper crumpling [28, 17]. This could give new insight into energy localisation phenomena in unstretchable sheets [5], which might help to predict points of onset of tearing. It could also aid our understanding of the rela- tionship between geometry and physical properties of nano- and microscopic M¨obius strip structures [26, 27, 11]. It is fair to say that the M¨obius strip is one of the few icons of mathematics that have been absorbed into wider culture. It has mathematical beauty and inspired artists such as M.C. Escher [8]. In engineering, pulley belts are often used in the form of M¨obius strips in order to wear ‘both’ sides equally. At a much smaller scale, M¨obius strips have recently been formed in ribbon-shaped NbSe3 crystals under certain growth 1Centre for Nonlinear Dynamics, Department of Civil and Environmental Engineering, University College London, London WC1E 6BT, UK Figure 1: Photo of a paper M¨obius strip of aspect ratio 2π.