DOCSLIB.ORG

Determining the Probability of Hemiplasy in the Presence of Incomplete Lineage Sorting and Introgression Supplementary Materials and Methods

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Determining the Probability of Hemiplasy in the Presence of Incomplete Lineage Sorting and Introgression Supplementary Materials and Methods Determining the probability of hemiplasy in the presence of incomplete lineage sorting and introgression Supplementary Materials and Methods Mark S. Hibbins*, Matthew J.S. Gibson*, and Matthew W. Hahn*† Department of Biology* and Department of Computer Science† Indiana University, Bloomington 1 Mutation probabilities on genealogies Each of the twelve possible genealogies under our parent tree model has a set of five branch lengths along which mutations can occur. l1, l2, and l3 denote the tip branches leading to species A, B, and C respectively; l4 denotes the internal branch, and l5 denotes the ancestral branch. As described in the supplement of Guerrero & Hahn (2018), the mu- tation probability on each of these branches has the general form R 1 − e−mx f (x)dx, where m is the mutation probability per 2N generations, x is the random variable for the branch length, and f(x) is the probability density function for x. We begin with the mutation probabilities for parent tree 1, which are found in the supple- ment of Guerrero & Hahn, and will be re-written here to be consistent with notation. In the following notation, parent tree 1 will be denoted as ”pt1”. Since many of the genealo- gies are identical in length, the mutation probabilities on their branches can be written with general expressions. We first consider the genealogies AB21, BC1, and AC1, which are all produced via incomplete lineage sorting in parent tree 1, and share the following set of mutation probabilities: 1 Z t3−t2 3 −m(t1+(t2−t1)+x) −x −3x n1[ILS, pt1] = (1 − e ) (e − e )dx (1) L 0 2 1 Z t3−t2 −m(t1+(t2−t1)+x) −3x −((t3−t2)−x) n2[ILS, pt1] = (1 − e )3e (1 − e )dx (2) L 0 t −t Z 3 2 Z (t −t )−y 1 −3y 3 2 −x −mx n4[ILS, pt1] = 3e ( e (1 − e )dx)dy (3) L 0 0 Z t3−t2 1 −m((t3−t2)−x) −3x n5[ILS, pt1] = (1 − e )3e dx (4) L 0 1 −3(t3−t2) 3 −(t3−t2) In each of the above, L = 1 + 2 e − 2 e is the probability of coalescence of A, B, and C in their ancestral population. t3 denotes the total height of the tree, i.e. the time at the base of the tree. The difference between t3 and t2 determines the duration of the ancestral population of all three taxa, before speciation occurs. Equations 1 through 4 each represent the mutation probabilities for multiple branches, which are as follows: n1[ILS, pt1] = n(l3, AB21) = n(l1, BC1) = n(l2, AC1) (5) 1 n2[ILS, pt1] = n(l1, AB21) = n(l2, AB21) = n(l2, BC1) = n(l3, BC1) = n(l1, AC1) = n(l3, AC1) (6) n4[ILS, pt1] = n(l4, AB21) = n(l4, BC1) = n(l4, AC1) (7) n5[ILS, pt1] = n(l5, AB21) = n(l5, BC1) = n(l5, AC1) (8) The gene tree produced by lineage sorting in parent tree 1, AB11, has a different set of mutation probabilities, since the branches have different expected lengths. These are: 1 Z t2−t1 ( ) = ( ) = ( − −m(t1+x)) −x n l1, AB11 n l2, AB11 −( − ) 1 e e dx (9) 1 − e t2 t1 0 1 Z t3−t2 ( ) = ( − −m(t1+(t2−t1)+x)) −x n l3, AB11 −( − ) 1 e e dx (10) 1 − e t3 t2 0 Z t2−t1 − − e y Z t3−t2 e x −m((t2−t1)−y+x) n(l4, AB11) = ( (1 − e ) dx)dy (11) −(t2−t1) −(t3−t2) 0 1 − e 0 1 − e 1 Z t3−t2 ( ) = ( − −m((t3−t2)−x)) −x n l5, AB11 −( − ) 1 e e dx (12) 1 − e t3 t2 0 Now we consider introgression, starting with parent tree 2. Many of the mutation proba- bilities are symmetrical with parent tree 1 and therefore remain the same, and the remain- der have the same general form with different parameters. For the ILS genealogies BC22, AB2, and AC2, equations 1 and 2 have the time of A-B speciation (t1) replaced with the timing of B-C introgression (tm). This gives: Z t3−t2 1 −m(tm+(t2−tm)+x) 3 −x −3x n1[ILS, pt2] = (1 − e ) (e − e )dx (13) L 0 2 Z t3−t2 1 −m(tm+(t2−tm)+x) −3x −((t3−t2)−x) n2[ILS, pt2] = (1 − e )3e (1 − e )dx (14) L 0 n4[ILS, pt2] = n4[ILS, pt1] (15) n5[ILS, pt2] = n5[ILS, pt1] (16) These correspond to the following branch mutation probabilities: n1[ILS, pt2] = n(l1, BC22) = n(l3, AB2) = n(l2, AC2) (17) n2[ILS, pt2] = n(l2, BC22) = n(l3, BC22) = n(l1, AB2) = n(l2, AB2) = n(l1, AC2) = n(l3, AC2) (18) n4[ILS, pt2] = n(l4, BC22) = n(l4, AB2) = n(l4, AC2) (19) n5[ILS, pt2] = n(l5, BC22) = n(l5, AB2) = n(l5, AC2) (20) 2 For the genealogy produced by lineage sorting in parent tree 2, BC12, we have: 1 Z t2−tm ( ) = ( ) = ( − −m(tm+x)) −x n l2, BC12 n l3, BC12 −( − ) 1 e e dx (21) 1 − e t2 tm 0 1 Z t3−t2 ( ) = ( − −m(tm+(t2−tm)+x)) −x n l1, BC12 −( − ) 1 e e dx (22) 1 − e t3 t2 0 Z t2−tm − − e y Z t3−t2 e x −m((t2−tm)−y+x) n(l4, BC12) = ( (1 − e ) dx)dy (23) −(t2−tm) −(t3−t2) 0 1 − e 0 1 − e n(l5, BC12) = n(l5, AB11) (24) Finally, we consider parent tree 3. The mutation probabilities have the same formulation as parent tree 2, with two key changes: since parent tree 3 is shorter (Figure 2 of main text), t2 is replaced by t1. This also applies to the value of L, which we will denote for 1 −3(t3−t1) 3 −(t3−t1) parent tree 3 as L3 = 1 + 2 e − 2 e . For the ILS genealogies BC23, AB3, and AC3, this gives: 1 Z t3−t1 3 −m(tm+(t1−tm)+x) −x −3x n1[ILS, pt3] = (1 − e ) (e − e )dx (25) L3 0 2 1 Z t3−t1 −m(tm+(t1−tm)+x) −3x −((t3−t1)−x) n2[ILS, pt3] = (1 − e )3e (1 − e )dx (26) L3 0 t −t Z 3 1 Z (t −t )−y 1 −3y 3 1 −x −mx n4[ILS, pt3] = 3e ( e (1 − e )dx)dy (27) L3 0 0 1 Z t3−t1 −m((t3−t1)−x) −3x n5[ILS, pt3] = (1 − e )3e dx (28) L3 0 Where: n1[ILS, pt3] = n(l1, BC23) = n(l3, AB3) = n(l2, BC3) (29) n2[ILS, pt3] = n(l2, BC23) = n(l3, BC23) = n(l1, AB3) = n(l2, AB3) = n(l1, AC3) = n(l3, AC3) (30) n4[ILS, pt3] = n(l4, BC23) = n(l4, AB3) = n(l4, AC3) (31) n5[ILS, pt3] = n(l5, BC23) = n(l5, AB3) = n(l5, AC3) (32) Finally, for the genealogy BC13, the mutation probabilities are as follows: 1 Z t1−tm ( ) = ( ) = ( − −m(tm+x)) −x n l2, BC13 n l3, BC13 −( − ) 1 e e dx (33) 1 − e t1 tm 0 1 Z t3−t1 ( ) = ( − −m(tm+(t1−tm)+x)) −x n l1, BC13 −( − ) 1 e e dx (34) 1 − e t3 t1 0 Z t1−tm − − e y Z t3−t1 e x −m((t1−tm)−y+x) n(l4, BC13) = ( (1 − e ) dx)dy (35) −(t1−tm) −(t3−t1) 0 1 − e 0 1 − e 1 Z t3−t1 ( ) = ( − −m((t3−t1)−x)) −x n l5, BC13 −( − ) 1 e e dx (36) 1 − e t3 t1 0 3 2 When does introgression makes hemiplasy more likely than ILS alone? The probability of hemiplasy with C ! B introgression is Pe = (1 − d)Pe[BC1] + d(Pe[BC12] + Pe[BC22]) (37) From this, it can be seen that introgression makes hemiplasy more likely than ILS alone when: Pe[BC12] + Pe[BC22] > Pe[BC1] (38) When is this true? Substituting the relevant expressions from the main text gives: −(t2−tm) (1 − e )v(l4, BC12) ∏(1 − v(li, BC12))+ i6=4 1 −(t2−tm) ( e )v(l4, BC22) ∏(1 − v(li, BC22)) 3 i6=4 1 −(t2−t1) > ( e )v(l4, BC1) ∏(1 − v(li, BC1)) (39) 3 i6=4 −(t2−tm) (1 − e )v(l4, BC12) ∏(1 − v(li, BC12)) > i6=4 1 −(t2−t1) ( e )v(l4, BC1) ∏(1 − v(li, BC1))− 3 i6=4 1 −(t2−tm) ( e )v(l4, BC22) ∏(1 − v(li, BC22)) (40) 3 i6=4 The mutation probabilities on the right side of the inequality are equal since they are on the same topology with the same branch lengths. Therefore, equation 40 can simplified: −(t2−tm) (1 − e )v(l4, BC12) ∏(1 − v(li, BC12)) > i6=4 1 1 −(t2−t1) −(t2−tm) v(l4, BC1) ∏(1 − v(li, BC1))( e − e ) (41) i6=4 3 3 As the most conservative case, let us assume a hybrid speciation scenario where t1 = tm. This represents the most conservative introgression scenario, since Figure 4 in the main text shows that more recent introgression makes hemiplasy more likely. In this case, the right side of the inequality simplifies to 0, leaving −(t2−tm) (1 − e )v(l4, BC12) ∏(1 − v(li, BC12)) > 0 (42) i6=4 This is true whenever t2 > tm, which is true by definition in this model. Therefore, intro- gression always makes hemiplasy more likely than ILS alone. 4 3 Supplementary Figures and Tables A) B) C) D) AB1 AB2 BC AC t t t t 2 2 2 2 t t t t 1 1 1 1 A B C A B C A B C ABC E) F) G) H) BC1! BC2! AB! AC! t t t t 2 2 2 2 t t t t m m m m A B C A BC A B C A B C Supplementary Figure 1: Each parent tree in our model generates four gene trees; one generated from lineage sorting (Panels A and E), and three equally likely trees generated from incomplete lineage sorting (panels B-D, F-H).
Load more

Recommended publications
  • VMAA-Performance-Sta
    Revised June 18, 2019 U.S. Department of Veterans Affairs (VA) Veteran Monthly Assistance Allowance for Disabled Veterans Training in Paralympic and Olympic Sports Program (VMAA) In partnership with the United States Olympic Committee and other Olympic and Paralympic entities within the United States, VA supports eligible service and non-service-connected military Veterans in their efforts to represent the USA at the Paralympic Games, Olympic Games and other international sport competitions. The VA Office of National Veterans Sports Programs & Special Events provides a monthly assistance allowance for disabled Veterans training in Paralympic sports, as well as certain disabled Veterans selected for or competing with the national Olympic Team, as authorized by 38 U.S.C. 322(d) and Section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program, VA will pay a monthly allowance to a Veteran with either a service-connected or non-service-connected disability if the Veteran meets the minimum military standards or higher (i.e. Emerging Athlete or National Team) in his or her respective Paralympic sport at a recognized competition. In addition to making the VMAA standard, an athlete must also be nationally or internationally classified by his or her respective Paralympic sport federation as eligible for Paralympic competition. VA will also pay a monthly allowance to a Veteran with a service-connected disability rated 30 percent or greater by VA who is selected for a national Olympic Team for any month in which the Veteran is competing in any event sanctioned by the National Governing Bodies of the Olympic Sport in the United State, in accordance with P.L.
    [Show full text]
  • Supporting Information Modular Control of L-Tryptophan Isotopic Substitution Via an Efficient Biosynthetic Cascade
    Electronic Supplementary Material (ESI) for Organic & Biomolecular Chemistry. This journal is © The Royal Society of Chemistry 2020 Supporting Information Modular Control of L-Tryptophan Isotopic Substitution via an Efficient Biosynthetic Cascade Thompson, C. M.; McDonald, A. D.; Yang, H.; Cavagnero, S.*; Buller, A. R.* Department of Chemistry, University of Wisconsin-Madison 1101 University Avenue Madison, WI 53706 *corresponding authors: Andrew R. Buller, email:[email protected]; Silvia Cavagnero, email: [email protected] Table of contents 1. General information 2 2. Experimental section 2 2.1 Materials 2 2.2 Methods 2 2.2.1 Cloning, expression, and purification of PfTrpB2B9 and TmLTA 2 2.2.2 Optimization of TmLTA-TrpB2B9 cascade 3 2.2.3 Preparative-scale synthesis of Trp isotopologs 4 2.2.4 Analytical- and preparative-scale chromatography 5 2.2.5 Determination of enantiopurity of Trp isotopologs 5 2.2.6 NMR analysis 6 3. Characterization of Trp and Trp isotopologs 7 4. Supporting references 10 5. Supporting tables and figures 11 - 17 − 1 − 1. General information The glassware used in the reactions carried out in this work was thoroughly washed, and all experiments were executed following necessary safety precautions. Evaporation of solvents was performed at reduced pressure using a rotary evaporator. Electronic-absorption measurements were done with a UV-2600 spectrophotometer (Shimadzu). 2. Experimental section 2.1. Materials Chemicals and solvents were obtained from commercial suppliers and used without further 13 purification: formaldehyde-D2 (Cambridge Isotope Laboratories, Inc.); (2- C)glycine (Cambridge Isotope Laboratories, Inc.); D2O 99.9% (Sigma-Aldrich); indole (Sigma- Aldrich); pyridoxal 5’ monophosphate; (Sigma-Aldrich) L-serine (Sigma-Aldrich).
    [Show full text]
  • The USANA Compensation Plan (Malaysia)
    The USANA Compensation Plan (Malaysia) Last revision: December, 2019 The USANA Compensation Plan encourages Figure 1. Distributors and Preferred Customers teamwork and ensures a fair distribution of income among Distributors, so you can build a stable leveraged income as your downline organisation grows. STARTING YOUR USANA BUSINESS YOU PreferredPC PreferredPC Customer Customer You start by joining as a member, your sponsor places you in an open position in his or her downline 1 3 4 2 organisation. As a USANA distributor, you may retail products to your friends, enroll them as Preferred Customers, or Distributor Distributor Distributor Distributor sponsor them into your organisation as Distributors (see Figure 1). In Malaysia, USANA allows you to build a maximum of four Distributor legs. AREAS OF INCOME: There are six ways to earn an income in USANA business: 3. WEEKLY COMMISSION (1) Retail Sales You earn weekly Commission based on the Group Sales (2) Front Line Commission Volume (GSV) of your global organisation. The GSV is the (3) Weekly Commission sum of all Sales Volume points from ALL the Distributors (4) Leadership Bonus and Preferred Customers in your organisation, irrespective (5) Elite Bonus of how many levels of referrals, and no matter where in the (6) Matching Bonus world they enroll. 1. RETAIL SALES The calculation for the Weekly Commission payout will be based on 20% of the total Group Sales Volume (GSV) You earn a retail profit by selling USANA products to your on the small side of the business.The minimum payout customers at the recommended retail prices which is 10% will be at 125 GSV and the maximum is 5000 GSV.
    [Show full text]
  • United States Olympic Committee and U.S. Department of Veterans Affairs
    SELECTION STANDARDS United States Olympic Committee and U.S. Department of Veterans Affairs Veteran Monthly Assistance Allowance Program The U.S. Olympic Committee supports Paralympic-eligible military veterans in their efforts to represent the USA at the Paralympic Games and other international sport competitions. Veterans who demonstrate exceptional sport skills and the commitment necessary to pursue elite-level competition are given guidance on securing the training, support, and coaching needed to qualify for Team USA and achieve their Paralympic dreams. Through a partnership between the United States Department of Veterans Affairs and the USOC, the VA National Veterans Sports Programs & Special Events Office provides a monthly assistance allowance for disabled Veterans of the Armed Forces training in a Paralympic sport, as authorized by 38 U.S.C. § 322(d) and section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program the VA will pay a monthly allowance to a Veteran with a service-connected or non-service-connected disability if the Veteran meets the minimum VA Monthly Assistance Allowance (VMAA) Standard in his/her respective sport and sport class at a recognized competition. Athletes must have established training and competition plans and are responsible for turning in monthly and/or quarterly forms and reports in order to continue receiving the monthly assistance allowance. Additionally, an athlete must be U.S. citizen OR permanent resident to be eligible. Lastly, in order to be eligible for the VMAA athletes must undergo either national or international classification evaluation (and be found Paralympic sport eligible) within six months of being placed on the allowance pay list.
    [Show full text]
  • Para Cycling Information Sheet About the Sport Classification Explained
    Para cycling information sheet About the sport Para cycling is cycling for people with impairments resulting from a health condition (disability). Para athletes with physical impairments either compete on handcycles, tricycles or bicycles, while those with a visual impairment compete on tandems with a sighted ‘pilot’. Para cycling is divided into track and road events, with seven events in total. Classification explained In Para sport classification provides the structure for fair and equitable competition to ensure that winning is determined by skill, fitness, power, endurance, tactical ability and mental focus – the same factors that account for success in sport for able-bodied athletes. The Para sport classification assessment process identifies the eligibility of each Para athlete’s impairment, and groups them into a sport class according to the degree of activity limitation resulting from their impairment. Classification is sport-specific as an eligible impairment affects a Para athlete’s ability to perform in different sports to a different extent. Each Para sport has a different classification system. Standard Classification in detail Para-Cycling sport classes include: Handcycle sport classes H1 – 5: There are five different sport classes for handcycle racing. The lower numbers indicate a more severe activity limitation. Para athletes competing in the H1 classes have a complete loss of trunk and leg function and limited arm function, e.g. as a result of a spinal cord injury. Para athletes in the H4 class have limited or no leg function, but good trunk and arm function. Para cyclists in sport classes H1 – 4 compete in a reclined position. Para cyclists in the H5 sport class sit on their knees because they are able to use their arms and trunk to accelerate the handcycle.
    [Show full text]
  • Para Cycling
    Cycling Canada Long-Term Development PARA-CYCLING i We acknowledge the financial support of the Government of Canada through Sport Canada, a branch of the Department of Canadian Heritage. CANADIAN CYCLING ASSOCIATION Long-Term Athlete Development: Para-cycling Contents 1 – Introduction . 2 2 – From Awareness to High Performance . 3 3 – Canada’s Para-cycling System: Overview and Para-cycling Stage by Stage . 10 4 – Building the Para-cycling System: Success Factors . 17 5 – Conclusion . 20 Resources and Contacts . 20 Acknowledgements Contributors: Mathieu Boucher, Stephen Burke, Julie Hutsebaut, Paul Jurbala, Sébastien Travers Assistance : Luc Arseneau, Louis Barbeau Credit : FQSC Para, No Accidental Champions, Photo from Rob Jones Document prepared by Paul Jurbala, communityactive Design: John Luimes, i . Design Group ISBN# 978-0-9809082-4-4 2013 CYCLING CANADA Long-Term Athlete Development: PARA-CYCLING 1 1 – Introduction Cycling Canada recognizes Long-Term Athlete Development (LTAD) as a corner- to providing LTAD-based programs from entry to Active for Life stages . Our stone for building cycling at all levels of competition and participation in Canada, goal is not simply to help Canadian Para-cyclists to be the best in the world, for athletes of all abilities . LTAD provides a progressive pathway for athletes to but to ensure that every athlete with an impairment can enjoy participation in optimize their development according to recognized stages and processes in cycling for a lifetime . human physical, mental, emotional, and cognitive maturation . LTAD is more than a model - it is a system and philosophy of sport development . The CCC’s Long-Term Athlete Development Guide presents a model for athlete LTAD is athlete-centered, coach-driven, and administration-supported .
    [Show full text]
  • (VA) Veteran Monthly Assistance Allowance for Disabled Veterans
    Revised May 23, 2019 U.S. Department of Veterans Affairs (VA) Veteran Monthly Assistance Allowance for Disabled Veterans Training in Paralympic and Olympic Sports Program (VMAA) In partnership with the United States Olympic Committee and other Olympic and Paralympic entities within the United States, VA supports eligible service and non-service-connected military Veterans in their efforts to represent the USA at the Paralympic Games, Olympic Games and other international sport competitions. The VA Office of National Veterans Sports Programs & Special Events provides a monthly assistance allowance for disabled Veterans training in Paralympic sports, as well as certain disabled Veterans selected for or competing with the national Olympic Team, as authorized by 38 U.S.C. 322(d) and Section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program, VA will pay a monthly allowance to a Veteran with either a service-connected or non-service-connected disability if the Veteran meets the minimum military standards or higher (i.e. Emerging Athlete or National Team) in his or her respective Paralympic sport at a recognized competition. In addition to making the VMAA standard, an athlete must also be nationally or internationally classified by his or her respective Paralympic sport federation as eligible for Paralympic competition. VA will also pay a monthly allowance to a Veteran with a service-connected disability rated 30 percent or greater by VA who is selected for a national Olympic Team for any month in which the Veteran is competing in any event sanctioned by the National Governing Bodies of the Olympic Sport in the United State, in accordance with P.L.
    [Show full text]
  • Should the Para-Cycling Classification System Be Reclassified?
    Should the para-cycling classification system be reclassified? David Borg1, John Osborne2, Johanna Liljedahl3, Michele Foster1, Carla Nooijen3 1The Hopkins Centre, Menzies Health Institute Queensland, Griffith University, Brisbane, Australia. 2School of Exercise and Nutrition Sciences, Queensland University of Technology, Brisbane, Australia. 3The Swedish School of Sport and Health Sciences (GIH), Stockholm, Sweden. Introduction Results Para-cycling athletes compete on bicycles (C1–5), handcycles The number of men in C1, C2, C3, C4 and C5 was 32, 76, 63, (H1–5) and tricycles (T1-2) in classes based on their functional 76, and 87, respectively. Nineteen men competed in T1 and 58 disability. Higher classes reflect less functional impairment. Para- in T2. The age range of men was 14–62 years. cycling classification is governed by the Union Cycliste Inter- The number of women competing in C1, C2, C3, C4 and C5 was nationale (UCI). The system aims to promote participation in the 4, 18, 16, 20 and 28, respectively. Eleven competed in T1 and sport, by controlling for the impact of impairment on the outcome 15 in T2. Women’s age ranged 17–55 years. of competition. Road race velocity for the bicycling and tricycling is shown in Recently, the separation between adjacent handcycling classes for Figure 1. Comparisons between adjacent classes for men and official UCI events was described––providing benchmarks for women are displayed in Table 2. active and potential athletes. Unfortunately, similar evaluation of the bicycling and tricycling disciplines has not been considered. With the expectation of C4 and C5 for women, the analysis showed that men's and women's road race performance was This study aimed to described the separation between adjacent statistically different between adjacent classes for bicycling and classes, based on performance, in UCI road race events for tricycling.
    [Show full text]
  • Fire Department Fiscal Year 2020 Annual Report July 1, 2019 – June 30, 2020
    Fire Department Fiscal Year 2020 Annual Report July 1, 2019 – June 30, 2020 Steven R. Goble Chief FIRE DEPARTMENT I. MISSION STATEMENT To preserve and protect life, property and the environment of Kaua‘i County from all hazards and emergencies. II. DEPARTMENT GOALS The Kaua‘i Fire Department (KFD) is dedicated and highly motivated to make our community safe. The KFD team has effectively carried out duties to achieve the department’s goals of preventing, suppressing and extinguishing all types of fires; responding to and mitigating any and all types of emergencies (medical, HAZMAT, search and rescue, disasters) in a highly trained, professional and safe manner; administering first aid and CPR to the basic life support level (EMT) and to make Kaua‘i a safer place by supporting and promoting training for the community; enforcing the National/Hawai‘i Fire Code and promote fire prevention through educational programs and community outreach; maintaining our vehicles and equipment for emergency response through a preventive maintenance program; and providing safe, guarded beaches through an effective and dynamic ocean safety program. III. PROGRAM DESCIPTION To accomplish these objectives, the department maintains a modern communications and record management system, conducts routine inspections, enforces and governs fire codes and regulations, conducts fire investigations to ascertain its origin and cause, promotes public awareness by providing on-going, up-to-date public education, advocates a structured and uniform fire training program which includes HAZMAT, CBRNE (chemical, biological, radiological, nuclear and explosive) and mountain and ocean search and rescue training, and promotes highly trained fire suppression and hazmat/rescue teams.
    [Show full text]
  • The Paralympic Athlete Dedicated to the Memory of Trevor Williams Who Inspired the Editors in 1997 to Write This Book
    This page intentionally left blank Handbook of Sports Medicine and Science The Paralympic Athlete Dedicated to the memory of Trevor Williams who inspired the editors in 1997 to write this book. Handbook of Sports Medicine and Science The Paralympic Athlete AN IOC MEDICAL COMMISSION PUBLICATION EDITED BY Yves C. Vanlandewijck PhD, PT Full professor at the Katholieke Universiteit Leuven Faculty of Kinesiology and Rehabilitation Sciences Department of Rehabilitation Sciences Leuven, Belgium Walter R. Thompson PhD Regents Professor Kinesiology and Health (College of Education) Nutrition (College of Health and Human Sciences) Georgia State University Atlanta, GA USA This edition fi rst published 2011 © 2011 International Olympic Committee Blackwell Publishing was acquired by John Wiley & Sons in February 2007. Blackwell’s publishing program has been merged with Wiley’s global Scientifi c, Technical and Medical business to form Wiley-Blackwell. Registered offi ce: John Wiley & Sons, Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK Editorial offi ces: 9600 Garsington Road, Oxford, OX4 2DQ, UK The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK 111 River Street, Hoboken, NJ 07030-5774, USA For details of our global editorial offi ces, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com/wiley-blackwell The right of the author to be identifi ed as the author of this work has been asserted in accordance with the UK Copyright, Designs and Patents Act 1988. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher.
    [Show full text]
  • TNM Classification of Malignant Tumours
    Table of Contents Cover Title Page Preface References Acknowledgments Organizations Associated with the TNM System Members of UICC Committees Associated with the TNM System Section Editors Introduction References Head and Neck Tumours Lip and Oral Cavity Pharynx References Larynx Nasal Cavity and Paranasal Sinuses Unknown Primary – Cervical Nodes Malignant Melanoma of Upper Aerodigestive Tract Major Salivary Glands Thyroid Gland Digestive System Tumours Oesophagus Stomach Reference Small Intestine Appendix Colon and Rectum Anal Canal and Perianal Skin Liver Intrahepatic Bile Ducts Gallbladder Perihilar Bile Ducts Distal Extrahepatic Bile Duct Ampulla of Vater Pancreas Well Differentiated Neuroendocrine Tumours of the Gastrointestinal Tract Lung, Pleural, and Thymic Tumours Lung References Pleural Mesothelioma Thymic Tumours References Tumours of Bone and Soft Tissues Bone Soft Tissues Gastrointestinal Stromal Tumour (GIST) Skin Tumours Carcinoma of Skin (excluding eyelid, head and neck, perianal, vulva, and penis) Skin Carcinoma of the Head and Neck Carcinoma of Skin of the Eyelid Malignant Melanoma of Skin Merkel Cell Carcinoma of Skin Breast Tumours Reference Gynaecological Tumours Reference Vulva Vagina Cervix Uteri Uterus – Endometrium Reference Uterine Sarcomas References Ovarian, Fallopian Tube, and Primary Peritoneal Carcinoma Reference Gestational Trophoblastic Neoplasms Reference Urological Tumours Penis Prostate References Testis Kidney Renal Pelvis and Ureter Urinary Bladder Urethra Adrenal Cortex (ICD O 3 C74.0) Ophthalmic
    [Show full text]
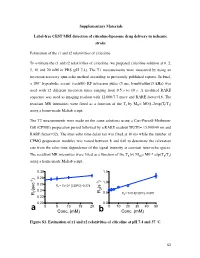
  • Conc. (Mm) B Conc
    Supplementary Materials Label-free CEST MRI detection of citicoline-liposome drug delivery in ischemic stroke Estimation of the r1 and r2 relaxivities of citicoline To estimate the r1 and r2 relaxivities of citicoline, we prepared citicoline solution at 0, 2, 5, 10 and 20 mM in PBS (pH 7.4). The T1 measurements were measured by using an inversion recovery spin-echo method according to previously published reports. In brief, a 180° hyperbolic secant (sech80) RF inversion pulse (5 ms, bandwidth=15 kHz) was used with 12 different inversion times ranging from 0.5 s to 10 s. A modified RARE sequence was used as imaging readout with 12,000/7.7 msec and RARE factor=16. The resultant MR intensities were fitted as a function of the TI by MTI= M0(1-2exp(TI/T1) using a home-made Maltab script. The T2 measurements were made on the same solutions using a Carr-Purcell-Meiboom- Gill (CPMG) preparation period followed by a RARE readout TR/TE= 15,000/40 ms and RARE factor=32). The inter-echo time delay tau was fixed at 10 ms while the number of CPMG preparation modules was varied between 8 and 640 to determine the relaxation rate from the echo time dependence of the signal intensity at constant inter-echo spaces. The resultant MR intensities were fitted as a function of the TE by MTE= M0 * exp(TE/T2) using a home-made Maltab script. 0.30 1.5 ) 0.28 ) -1 1.0 0.26 -4 -1 R1= 7x10 [CDPC]+0.274 (s 2 (sec 1 0.24 R 0.5 R = 0.014[CDPC]+0.591 R 2 0.22 0.20 0.0 a 0 5 10 15 20 0 10 20 30 40 50 Conc.
    [Show full text]