Video Coding
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Method for Compensating for Color Differences Between Different Images of a Same Scene
(19) TZZ¥ZZ__T (11) EP 3 001 668 A1 (12) EUROPEAN PATENT APPLICATION (43) Date of publication: (51) Int Cl.: 30.03.2016 Bulletin 2016/13 H04N 1/60 (2006.01) (21) Application number: 14306471.5 (22) Date of filing: 24.09.2014 (84) Designated Contracting States: (72) Inventors: AL AT BE BG CH CY CZ DE DK EE ES FI FR GB • Sheikh Faridul, Hasan GR HR HU IE IS IT LI LT LU LV MC MK MT NL NO 35576 CESSON-SÉVIGNÉ (FR) PL PT RO RS SE SI SK SM TR • Stauder, Jurgen Designated Extension States: 35576 CESSON-SÉVIGNÉ (FR) BA ME • Serré, Catherine 35576 CESSON-SÉVIGNÉ (FR) (71) Applicants: • Tremeau, Alain • Thomson Licensing 42000 SAINT-ETIENNE (FR) 92130 Issy-les-Moulineaux (FR) • CENTRE NATIONAL DE (74) Representative: Browaeys, Jean-Philippe LA RECHERCHE SCIENTIFIQUE -CNRS- Technicolor 75794 Paris Cedex 16 (FR) 1, rue Jeanne d’Arc • Université Jean Monnet de Saint-Etienne 92443 Issy-les-Moulineaux (FR) 42023 Saint-Etienne Cedex 2 (FR) (54) Method for compensating for color differences between different images of a same scene (57) The method comprises the steps of: - for each combination of a first and second illuminants, applying its corresponding chromatic adaptation matrix to the colors of a first image to compensate such as to obtain chromatic adapted colors forming a chromatic adapted image and calculating the difference between the colors of a second image and the chromatic adapted colors of this chromatic adapted image, - retaining the combination of first and second illuminants for which the corresponding calculated difference is the smallest, - compensating said color differences by applying the chromatic adaptation matrix corresponding to said re- tained combination to the colors of said first image. -

Book of Abstracts of the International Colour Association (AIC) Conference 2020
NATURAL COLOURS - DIGITAL COLOURS Book of Abstracts of the International Colour Association (AIC) Conference 2020 Avignon, France 20, 26-28th november 2020 Sponsored by le Centre Français de la Couleur (CFC) Published by International Colour Association (AIC) This publication includes abstracts of the keynote, oral and poster papers presented in the International Colour Association (AIC) Conference 2020. The theme of the conference was Natural Colours - Digital Colours. The conference, organised by the Centre Français de la Couleur (CFC), was held in Avignon, France on 20, 26-28th November 2020. That conference, for the first time, was managed online and onsite due to the sanitary conditions provided by the COVID-19 pandemic. More information in: www.aic2020.org. © 2020 International Colour Association (AIC) International Colour Association Incorporated PO Box 764 Newtown NSW 2042 Australia www.aic-colour.org All rights reserved. DISCLAIMER Matters of copyright for all images and text associated with the papers within the Proceedings of the International Colour Association (AIC) 2020 and Book of Abstracts are the responsibility of the authors. The AIC does not accept responsibility for any liabilities arising from the publication of any of the submissions. COPYRIGHT Reproduction of this document or parts thereof by any means whatsoever is prohibited without the written permission of the International Colour Association (AIC). All copies of the individual articles remain the intellectual property of the individual authors and/or their -

International Journal for Scientific Research & Development
IJSRD - International Journal for Scientific Research & Development| Vol. 1, Issue 12, 2014 | ISSN (online): 2321-0613 Modifying Image Appearance for Improvement in Information Gaining For Colour Blinds Prof.D.S.Khurge1 Bhagyashree Peswani2 1Professor, ME2, 1, 2 Department of Electronics and Communication, 1,2L.J. Institute of Technology, Ahmedabad Abstract--- Color blindness is a color perception problem of Light transmitted by media i.e., Television uses additive human eye to distinguish colors. Persons who are suffering color mixing with primary colors of red, green, and blue, from color blindness face many problem in day to day life each of which is stimulating one of the three types of the because many information are contained in color color receptors of eyes with as little stimulation as possible representations like traffic light, road signs etc. of the other two. Its called "RGB" color space. Mixtures of Daltonization is a procedure for adapting colors in an image light are actually a mixture of these primary colors and it or a sequence of images for improving the color perception covers a huge part of the human color space and thus by a color-deficient viewer. In this paper, we propose a re- produces a large part of human color experiences. That‟s coloring algorithm to improve the accessibility for the color because color television sets or color computer monitors deficient viewers. In Particular, we select protanopia, a type needs to produce mixtures of primary colors. of dichromacy where the patient does not naturally develop Other primary colors could in principle be used, but the “Red”, or Long wavelength, cones in his or her eyes. -

Application of Contrast Sensitivity Functions in Standard and High Dynamic Range Color Spaces
https://doi.org/10.2352/ISSN.2470-1173.2021.11.HVEI-153 This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Color Threshold Functions: Application of Contrast Sensitivity Functions in Standard and High Dynamic Range Color Spaces Minjung Kim, Maryam Azimi, and Rafał K. Mantiuk Department of Computer Science and Technology, University of Cambridge Abstract vision science. However, it is not obvious as to how contrast Contrast sensitivity functions (CSFs) describe the smallest thresholds in DKL would translate to thresholds in other color visible contrast across a range of stimulus and viewing param- spaces across their color components due to non-linearities such eters. CSFs are useful for imaging and video applications, as as PQ encoding. contrast thresholds describe the maximum of color reproduction In this work, we adapt our spatio-chromatic CSF1 [12] to error that is invisible to the human observer. However, existing predict color threshold functions (CTFs). CTFs describe detec- CSFs are limited. First, they are typically only defined for achro- tion thresholds in color spaces that are more commonly used in matic contrast. Second, even when they are defined for chromatic imaging, video, and color science applications, such as sRGB contrast, the thresholds are described along the cardinal dimen- and YCbCr. The spatio-chromatic CSF model from [12] can sions of linear opponent color spaces, and therefore are difficult predict detection thresholds for any point in the color space and to relate to the dimensions of more commonly used color spaces, for any chromatic and achromatic modulation. -

A Novel Technique for Modification of Images for Deuteranopic Viewers
ISSN (Online) 2278-1021 IJARCCE ISSN (Print) 2319 5940 International Journal of Advanced Research in Computer and Communication Engineering Vol. 5, Issue 4, April 2016 A Novel Technique for Modification of Images for Deuteranopic Viewers Jyoti D. Badlani1, Prof. C.N. Deshmukh 2 PG Student [Dig Electronics], Dept. of Electronics & Comm. Engineering, PRMIT&R, Badnera, Amravati, Maharashtra, India1 Professor, Dept. of Electronics & Comm. Engineering, PRMIT&R, Badnera, Amravati, Maharashtra, India2 Abstract: About 8% of men and 0.5% women in world are affected by the Colour Vision Deficiency. As per the statistics, there are nearly 200 million colour blind people in the world. Color vision deficient people are liable to missing some information that is taken by color. People with complete color blindness can only view things in white, gray and black. Insufficiency of color acuity creates many problems for the color blind people, from daily actions to education. Color vision deficiency, is a condition in which the affected individual cannot differentiate between colors as well as individuals without CVD. Colour vision deficiency, predominantly caused by hereditary reasons, while, in some rare cases, is believed to be acquired by neurological injuries. A colour vision deficient will miss out certain critical information present in the image or video. But with the aid of Image processing, many methods have been developed that can modify the image and thus making it suitable for viewing by the person suffering from CVD. Color adaptation tools modify the colors used in an image to improve the discrimination of colors for individuals with CVD. This paper enlightens some previous research studies in this field and follows the advancement that has occurred over the time. -

Dark Image Enhancement Using Perceptual Color Transfer
IEEE Access, vol. 5, 2017, pp. 1-1. Dark image enhancement using perceptual color transfer. Cepeda-Negrete, J., Sanchez-Yanez, RE., Correa-Tome, Fernando E y Lizarraga-Morales, Rocio A. Cita: Cepeda-Negrete, J., Sanchez-Yanez, RE., Correa-Tome, Fernando E y Lizarraga-Morales, Rocio A (2017). Dark image enhancement using perceptual color transfer. IEEE Access, 5 1-1. Dirección estable: https://www.aacademica.org/jcepedanegrete/14 Esta obra está bajo una licencia de Creative Commons. Para ver una copia de esta licencia, visite http://creativecommons.org/licenses/by-nc-nd/4.0/deed.es. Acta Académica es un proyecto académico sin fines de lucro enmarcado en la iniciativa de acceso abierto. Acta Académica fue creado para facilitar a investigadores de todo el mundo el compartir su producción académica. Para crear un perfil gratuitamente o acceder a otros trabajos visite: http://www.aacademica.org. Received September 21, 2017, accepted October 13, 2017. Date of publication xxxx 00, 0000, date of current version xxxx 00, 0000. Digital Object Identifier 10.1109/ACCESS.2017.2763898 Dark Image Enhancement Using Perceptual Color Transfer JONATHAN CEPEDA-NEGRETE 1, RAUL E. SANCHEZ-YANEZ 2, (Member, IEEE), FERNANDO E. CORREA-TOME2, AND ROCIO A. LIZARRAGA-MORALES3, (Member, IEEE) AQ:1 1Department of Agricultural Engineering, University of Guanajuato DICIVA, Guanajuato 36500 , Mexico 2Department of Electronics Engineering, University of Guanajuato DICIS, Guanajuato 36500, Mexico 3Department of Multidisciplinary Studies, University of Guanajuato DICIS, Guanajuato 36500, Mexico Corresponding author: Raul E. Sanchez-Yanez ([email protected]) The work of J. Cepeda-Negrete was supported by the Mexican National Council on Science and Technology (CONACyT) through the Scholarship 290747 under Grant 388681/254884. -

Color Blindness Bartender: an Embodied VR Game Experience
2020 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW) Color Blindness Bartender: An Embodied VR Game Experience Zhiquan Wang* Huimin Liu† Yucong Pan‡ Christos Mousas§ Department of Computer Graphics Technology Purdue University, West Lafayette, Indiana, U.S.A. ABSTRACT correction [4]. Many color blindness test applications have been Color blindness is a very common condition, as almost one in ten summarized in Plothe [13]. For example, color-vision adaptation people have some level of color blindness or visual impairment. methods for digital game have been developed to assist people with However, there are many tasks in daily life that require the abilities color-blindness [12]. of color recognition and visual discrimination. In order to understand 2.1 Colorblindness Types the inconvenience that color-blind people experience in daily life, we developed a virtual reality (VR) application that provides the sense Cone cells are responsible for color recognition. There are three of embodiment of a color-blind person. Specifically, we designed a types of cones [2], which respond to low, medium, and long wave- color-based task for users to complete under different types of color lengths, respectively, and missing one of the cone types results in one blindness in which users make colorful cocktails for customers and of three different kinds of color blindness: tritanopia, deuteranopia, need to switch between different color blindness modalities of the and protanopia. Tritanopia refers to missing short-wavelength cones, application to distinguish different colors. Our application aims to and results in an inability to distinguish the colors of blue and yellow. -

Increasing Web Accessibility Through an Assisted Color Specification Interface for Colorblind People
Interaction Design and Architecture(s) Journal - IxD&A, N. 5-6, 2009, pp. 41-48 Increasing Web accessibility through an assisted color specification interface for colorblind people Antonella Foti Giuseppe Santucci Dipartimento di Informatica e Sistemistica Dipartimento di Informatica e Sistemistica Sapienza Università degli studi di Roma Sapienza Università degli studi di Roma [email protected] [email protected] 1. In order to be effective it focuses on a subset of the ABSTRACT accessibility issues, dealing with problems associated Nowadays web accessibility refers mainly to users with severe with hypo-sight and colorblindness. In fact, it is the disabilities, neglecting colorblind people, i.e., people lacking a authors' belief that, in order to address affectively chromatic dimension at receptor level. As a consequence, a wrong accessibility issues, it is mandatory to focus on a usage of colors in a web site, in terms of red or green, together specific class of users at a time, addressing only the with blue or yellow, may result in a loss of information. Color problems that are relevant for that class. As an example, models and color selection strategies proposed so far fail to while dealing with colorblind people it is crucial to accurately address such issues. This article describes a module of ensure color separation between plain text and the VisAwis (VISual Accessibility for Web Interfaces) project hyperlink text; such an activity is totally useless for that, following a compromise between usability and accessibility, people impaired by hypo-sight. allow color blind people to select distinguishable colors taking 2. It defines a set of strategies and metrics to automatically into account their specific missing receptor. -

Newton's Conclusions
12/4/2013 Newton’s Color Experiments 1671 Newton’s Conclusions • White light has seven constituent components: red, orange, yellow, green, blue, indigo and violet. • Dispersed light can be recombined to form white light. • Magenta and purple can be obtained by combining only portions of the spectrum. 1 12/4/2013 Color and Color Vision The perceived color of an object depends on four factors: 1. Spectrum of the illumination source 2. Spectral Reflectance of the object 3. Spectral response of the photoreceptors (including bleaching) 4. Interactions between photoreceptors Light Sources Spectral Spectral Spectral Output Output Output nm nm nm 400 700 400 700 400 700 White Monochromatic Colored 2 12/4/2013 Pigments Spectral Spectral Spectral Reflectance Reflectance Reflectance nm nm nm 400 700 400 700 400 700 Red Green Blue Subtractive Colors Pigments (e.g. paints and inks) absorb different portions of the spectrum Spectral Spectral Spectral Multiply the spectrum Output Output Output of the light source by the spectral reflectivity of the object to find nm nm nm the distribution 400 700 400 700 400 700 entering the eye. nm nm nm 400 700 400 700 400 700 3 12/4/2013 Blackbody Radiation For lower temperatures, blackbodies appear red. As they heat up, the shift through the spectrum towards blue. Our sun looks like a 6500K blackbody. Incandescent lights are poor efficiency blackbodies radiators. Gas‐Discharge & Fluorescent Lamps A low pressure gas or vapor is encased in a glass tube. Electrical connections are made at the ends of the tube. Electrical discharge excites the atoms and they emit in a series of spectral lines. -

Dark Image Enhancement Using Perceptual Color Transfer
Received September 21, 2017, accepted October 13, 2017, date of publication October 17, 2017, date of current version April 4, 2018. Digital Object Identifier 10.1109/ACCESS.2017.2763898 Dark Image Enhancement Using Perceptual Color Transfer JONATHAN CEPEDA-NEGRETE 1, RAUL E. SANCHEZ-YANEZ 2, (Member, IEEE), FERNANDO E. CORREA-TOME2, AND ROCIO A. LIZARRAGA-MORALES3, (Member, IEEE) 1Department of Agricultural Engineering, University of Guanajuato DICIVA, Irapuato, Gto. 36500, Mexico 2Department of Electronics Engineering, University of Guanajuato DICIS, Salamanca, Gto. 36885, Mexico 3Department of Multidisciplinary Studies, University of Guanajuato DICIS, Yuriria, Gto. 38944, Mexico Corresponding author: Raul E. Sanchez-Yanez ([email protected]) The work of J. Cepeda-Negrete was supported by the Mexican National Council on Science and Technology (CONACyT) through the Scholarship 290747 under Grant 388681/254884. ABSTRACT In this paper, we introduce an image enhancing approach for transforming dark images into lightened scenes, and we evaluate such method in different perceptual color spaces, in order to find the best-suited for this particular task. Specifically, we use a classical color transfer method where we obtain first-order statistics from a target image and transfer them to a dark input, modifying its hue and brightness. Two aspects are particular to this paper, the application of color transfer on dark imagery and in the search for the best color space for the application. In this regard, the tests performed show an accurate transference of colors when using perceptual color spaces, being RLAB the best color space for the procedure. Our results show that the methodology presented in this paper can be a good alternative to low-light or night vision processing techniques. -
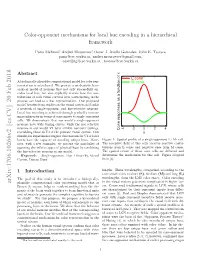
Color-Opponent Mechanisms for Local Hue Encoding in a Hierarchical Framework
Color-opponent mechanisms for local hue encoding in a hierarchical framework Paria Mehrani,∗ Andrei Mouraviev,∗ Oscar J. Avella Gonzalez, John K. Tsotsos [email protected], [email protected], [email protected] , [email protected] Abstract L cone A biologically plausible computational model for color rep- M cone resentation is introduced. We present a mechanistic hier- archical model of neurons that not only successfully en- codes local hue, but also explicitly reveals how the con- tributions of each visual cortical layer participating in the process can lead to a hue representation. Our proposed model benefits from studies on the visual cortex and builds a network of single-opponent and hue-selective neurons. Local hue encoding is achieved through gradually increas- ing nonlinearity in terms of cone inputs to single-opponent cells. We demonstrate that our model's single-opponent neurons have wide tuning curves, while the hue-selective neurons in our model V4 layer exhibit narrower tunings, Cone responses as a function of x -4 -2 0 2 4 resembling those in V4 of the primate visual system. Our x simulation experiments suggest that neurons in V4 or later layers have the capacity of encoding unique hues. More- Figure 1: Spatial profile of a single-opponent L+M- cell. over, with a few examples, we present the possibility of The receptive field of this cells receives positive contri- spanning the infinite space of physical hues by combining butions from L cones and negative ones from M cones. the hue-selective neurons in our model. The spatial extent of these cone cells are different and Keywords| Single-opponent, Hue, Hierarchy, Visual determines the mechanism for this cell. -

High-Throughput Fast Full-Color Digital Pathology Based on Fourier Ptychographic Microscopy Via Color Transfer
High-throughput fast full-color digital pathology based on Fourier ptychographic microscopy via color transfer Yuting Gao,a,b Jiurun Chen,a,b Aiye Wang,a,b An Pan,a,* Caiwen Ma,a,* Baoli Yaoa a Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an 710119, China b University of Chinese Academy of Sciences, Beijing 100049, China Abstract. Full-color imaging is significant in digital pathology. Compared with a grayscale image or a pseudo-color image that only contains the contrast information, it can identify and detect the target object better with color texture information. Fourier ptychographic microscopy (FPM) is a high-throughput computational imaging technique that breaks the tradeoff between high resolution (HR) and large field-of-view (FOV), which eliminates the artifacts of scanning and stitching in digital pathology and improves its imaging efficiency. However, the conventional full-color digital pathology based on FPM is still time-consuming due to the repeated experiments with tri-wavelengths. A color transfer FPM approach, termed CFPM was reported. The color texture information of a low resolution (LR) full-color pathologic image is directly transferred to the HR grayscale FPM image captured by only a single wavelength. The color space of FPM based on the standard CIE-XYZ color model and display based on the standard RGB (sRGB) color space were established. Different FPM colorization schemes were analyzed and compared with thirty different biological samples. The average root-mean-square error (RMSE) of the conventional method and CFPM compared with the ground truth is 5.3% and 5.7%, respectively.