On the Galactic Disk Metallicity Distribution from Open Clusters I
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Basic Requirement for Studying the Heavens Is Determining Where In
Abasic requirement for studying the heavens is determining where in the sky things are. To specify sky positions, astronomers have developed several coordinate systems. Each uses a coordinate grid projected on to the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle (the fundamental plane of the geographic system is the Earth's equator) . Each coordinate system is named for its choice of fundamental plane. The equatorial coordinate system is probably the most widely used celestial coordinate system. It is also the one most closely related to the geographic coordinate system, because they use the same fun damental plane and the same poles. The projection of the Earth's equator onto the celestial sphere is called the celestial equator. Similarly, projecting the geographic poles on to the celest ial sphere defines the north and south celestial poles. However, there is an important difference between the equatorial and geographic coordinate systems: the geographic system is fixed to the Earth; it rotates as the Earth does . The equatorial system is fixed to the stars, so it appears to rotate across the sky with the stars, but of course it's really the Earth rotating under the fixed sky. The latitudinal (latitude-like) angle of the equatorial system is called declination (Dec for short) . It measures the angle of an object above or below the celestial equator. The longitud inal angle is called the right ascension (RA for short). -

Proto-Planetary Nebula Observing Guide
Proto-Planetary Nebula Observing Guide www.reinervogel.net RA Dec CRL 618 Westbrook Nebula 04h 42m 53.6s +36° 06' 53" PK 166-6 1 HD 44179 Red Rectangle 06h 19m 58.2s -10° 38' 14" V777 Mon OH 231.8+4.2 Rotten Egg N. 07h 42m 16.8s -14° 42' 52" Calabash N. IRAS 09371+1212 Frosty Leo 09h 39m 53.6s +11° 58' 54" CW Leonis Peanut Nebula 09h 47m 57.4s +13° 16' 44" Carbon Star with dust shell M 2-9 Butterfly Nebula 17h 05m 38.1s -10° 08' 33" PK 10+18 2 IRAS 17150-3224 Cotton Candy Nebula 17h 18m 20.0s -32° 27' 20" Hen 3-1475 Garden-sprinkler Nebula 17h 45m 14. 2s -17° 56' 47" IRAS 17423-1755 IRAS 17441-2411 Silkworm Nebula 17h 47m 13.5s -24° 12' 51" IRAS 18059-3211 Gomez' Hamburger 18h 09m 13.3s -32° 10' 48" MWC 922 Red Square Nebula 18h 21m 15s -13° 01' 27" IRAS 19024+0044 19h 05m 02.1s +00° 48' 50.9" M 1-92 Footprint Nebula 19h 36m 18.9s +29° 32' 50" Minkowski's Footprint IRAS 20068+4051 20h 08m 38.5s +41° 00' 37" CRL 2688 Egg Nebula 21h 02m 18.8s +36° 41' 38" PK 80-6 1 IRAS 22036+5306 22h 05m 30.3s +53° 21' 32.8" IRAS 23166+1655 23h 19m 12.6s +17° 11' 33.1" Southern Objects ESO 172-7 Boomerang Nebula 12h 44m 45.4s -54° 31' 11" Centaurus bipolar nebula PN G340.3-03.2 Water Lily Nebula 17h 03m 10.1s -47° 00' 27" PK 340-03 1 IRAS 17163-3907 Fried Egg Nebula 17h 19m 49.3s -39° 10' 37.9" Finder charts measure 20° (with 5° circle) and 5° (with 1° circle) and were made with Cartes du Ciel by Patrick Chevalley (http://www.ap-i.net/skychart) Images are DSS Images (blue plates, POSS II or SERCJ) and measure 30’ by 30’ (http://archive.stsci.edu/cgi- bin/dss_plate_finder) and STScI Images (Hubble Space Telescope) Downloaded from www.reinervogel.net version 12/2012 DSS images copyright notice: The Digitized Sky Survey was produced at the Space Telescope Science Institute under U.S. -

Atlas Menor Was Objects to Slowly Change Over Time
C h a r t Atlas Charts s O b by j Objects e c t Constellation s Objects by Number 64 Objects by Type 71 Objects by Name 76 Messier Objects 78 Caldwell Objects 81 Orion & Stars by Name 84 Lepus, circa , Brightest Stars 86 1720 , Closest Stars 87 Mythology 88 Bimonthly Sky Charts 92 Meteor Showers 105 Sun, Moon and Planets 106 Observing Considerations 113 Expanded Glossary 115 Th e 88 Constellations, plus 126 Chart Reference BACK PAGE Introduction he night sky was charted by western civilization a few thou - N 1,370 deep sky objects and 360 double stars (two stars—one sands years ago to bring order to the random splatter of stars, often orbits the other) plotted with observing information for T and in the hopes, as a piece of the puzzle, to help “understand” every object. the forces of nature. The stars and their constellations were imbued with N Inclusion of many “famous” celestial objects, even though the beliefs of those times, which have become mythology. they are beyond the reach of a 6 to 8-inch diameter telescope. The oldest known celestial atlas is in the book, Almagest , by N Expanded glossary to define and/or explain terms and Claudius Ptolemy, a Greco-Egyptian with Roman citizenship who lived concepts. in Alexandria from 90 to 160 AD. The Almagest is the earliest surviving astronomical treatise—a 600-page tome. The star charts are in tabular N Black stars on a white background, a preferred format for star form, by constellation, and the locations of the stars are described by charts. -
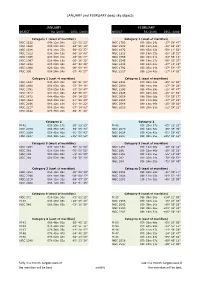
SPIRIT Target Lists
JANUARY and FEBRUARY deep sky objects JANUARY FEBRUARY OBJECT RA (2000) DECL (2000) OBJECT RA (2000) DECL (2000) Category 1 (west of meridian) Category 1 (west of meridian) NGC 1532 04h 12m 04s -32° 52' 23" NGC 1792 05h 05m 14s -37° 58' 47" NGC 1566 04h 20m 00s -54° 56' 18" NGC 1532 04h 12m 04s -32° 52' 23" NGC 1546 04h 14m 37s -56° 03' 37" NGC 1672 04h 45m 43s -59° 14' 52" NGC 1313 03h 18m 16s -66° 29' 43" NGC 1313 03h 18m 15s -66° 29' 51" NGC 1365 03h 33m 37s -36° 08' 27" NGC 1566 04h 20m 01s -54° 56' 14" NGC 1097 02h 46m 19s -30° 16' 32" NGC 1546 04h 14m 37s -56° 03' 37" NGC 1232 03h 09m 45s -20° 34' 45" NGC 1433 03h 42m 01s -47° 13' 19" NGC 1068 02h 42m 40s -00° 00' 48" NGC 1792 05h 05m 14s -37° 58' 47" NGC 300 00h 54m 54s -37° 40' 57" NGC 2217 06h 21m 40s -27° 14' 03" Category 1 (east of meridian) Category 1 (east of meridian) NGC 1637 04h 41m 28s -02° 51' 28" NGC 2442 07h 36m 24s -69° 31' 50" NGC 1808 05h 07m 42s -37° 30' 48" NGC 2280 06h 44m 49s -27° 38' 20" NGC 1792 05h 05m 14s -37° 58' 47" NGC 2292 06h 47m 39s -26° 44' 47" NGC 1617 04h 31m 40s -54° 36' 07" NGC 2325 07h 02m 40s -28° 41' 52" NGC 1672 04h 45m 43s -59° 14' 52" NGC 3059 09h 50m 08s -73° 55' 17" NGC 1964 05h 33m 22s -21° 56' 43" NGC 2559 08h 17m 06s -27° 27' 25" NGC 2196 06h 12m 10s -21° 48' 22" NGC 2566 08h 18m 46s -25° 30' 02" NGC 2217 06h 21m 40s -27° 14' 03" NGC 2613 08h 33m 23s -22° 58' 22" NGC 2442 07h 36m 20s -69° 31' 29" Category 2 Category 2 M 42 05h 35m 17s -05° 23' 25" M 42 05h 35m 17s -05° 23' 25" NGC 2070 05h 38m 38s -69° 05' 39" NGC 2070 05h 38m 38s -69° -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Southern Sky Binocular Observing List
Southern Sky Binocular Observing List Object R.A. DEC Mag PA* Type Size Const Urn SA [ ] NGC 104 00 24.1 -72 05 4.5 ----- GbCl 25.0' Tuc 440 24 [ ] SMC 00 52.8 -72 50 2.7 10 Glxy 316'X186' Tuc 441 24 [ ] NGC 362 01 03.2 -70 51 6.6 ----- GbCl 12.9' Tuc 441 24 [ ] NGC 1261 03 12.3 -55 13 8.4 ----- GbCl 6.9' Hor 419 24 [ ] NGC 1851 05 14.1 -40 03 7.2 ----- GbCl 11.0' Col 393 19 [ ] LMC 05 23.6 -69 45 0.9 170 Glxy 646'X550' Dor 444 24 [ ] NGC 2070 05 38.6 -69 05 8.2 ----- BNeb 40'X25' Dor 445 24 [ ] NGC 2451 07 45.4 -37 58 2.8 ----- OpCl 45.0' Pup 362 19 [ ] NGC 2477 07 52.3 -38 33 5.8 ----- OpCl 27.0' Pup 362 19 [ ] NGC 2516 07 58.3 -60 52 3.8 ----- OpCl 29.0' Car 424 24 [ ] NGC 2547 08 10.7 -49 16 4.7 ----- OpCl 20.0' Vel 396 20 [ ] NGC 2546 08 12.4 -37 38 6.3 ----- OpCl 40.0' Pup 362 20 [ ] NGC 2627 08 37.3 -29 57 8.4 ----- OpCl 11.0' Pyx 363 20 [ ] IC 2391 08 40.2 -53 04 2.5 ----- OpCl 50.0' Vel 425 25 [ ] IC 2395 08 41.1 -48 12 4.6 ----- OpCl 7.0' Vel 397 20 [ ] NGC 2659 08 42.6 -44 57 8.6 ----- OpCl 2.7' Vel 397 20 [ ] NGC 2670 08 45.5 -48 47 7.8 ----- OpCl 9.0' Vel 397 20 [ ] NGC 2808 09 12.0 -64 52 6.3 ----- GbCl 13.8' Car 448 25 [ ] IC 2488 09 27.6 -56 59 7.4 ----- OpCl 14.0' Vel 425 25 [ ] NGC 2910 09 30.4 -52 54 7.2 ----- OpCl 5.0' Vel 426 25 [ ] NGC 2925 09 33.7 -53 26 8.3 ----- OpCl 12.0' Vel 426 25 [ ] NGC 3114 10 02.7 -60 07 4.2 ----- OpCl 35.0' Car 426 25 [ ] NGC 3201 10 17.6 -46 25 6.7 ----- GbCl 18.0' Vel 399 20 [ ] NGC 3228 10 21.8 -51 43 6.0 ----- OpCl 18.0' Vel 426 25 [ ] NGC 3293 10 35.8 -58 14 4.7 ----- OpCl 5.0' Car -

Skytools Chart
36 Ara - Pavo SkyTools 3 / Skyhound.com 2 ζ 6541 NGC 6231 ζ NGC 6124 θ NGC 6322 η η 6496 ζ 1 6388 PK 345-04.1 -4 NGC 6259 NGC 6192 0° 1 ε NGC 6249 ι 1 δ α PK 342-04.1 β IC 4699 μ σ Mu Normae Cluster β2 NGC 6250 NGC 6178 NGC 6204 6352 ω NGC 6200 δ ζ λ θ α IC 4651 NGC 6193 ε ι PK 342-14.1 NGC 6134 6584 6326 NGC 6167 2 Ara γ η 6397 γ1 λ ε1 NGC 6152 α NGC 6208 1 ν μ β 5946 γ ζ NGC 6067 -50° ξ PK 331-05.1 κ 5927 PK 329-02.2 η ζ η NGC 6087 NGC 5999 NGC 5925 Pavo Globular δ 6221 ι1 ξ Collinder 292 α NGC 5822 ν λ 6300 NGC 5823 NGC 6025 π NGC 5749 6744 η PK 325-12.1 γ β β φ1 Pavo δ β NGC 5662 ρ 6362 κ ζ Circinus δ Triangulum Australe ε α Rigel Kentaurus ε 5844 2 -6 α 0 ° β NGC 5617 ζ ζ α Agena 6101 γ γ NGC 5316 ε Apus PK 315-13.1 -7 0° NGC 5281 2 1h h 5 52° x 34° 1 18h 18h00m00.0s -60°00'00" (Skymark) Globular Cl. Dark Neb. Galaxy 8 7 6 5 4 3 2 1 Globule Planetary Open Cl. Nebula 36 Ara - Pavo GALASSIE Sigla Nome Cost. A.R. Dec. Mv. Dim. Tipo Distanza 200/4 80/11,5 20x60 NGC 6221 Ara 16h 52m 47s -59° 12' 59" +10,70 4',6x2',8 Sc 18,0 Mly --- --- --- NGC 6300 Ara 17h 16m 59s -62° 49' 11" +11,00 5',5x3',5 SBb 34,0 Mly --- --- --- NGC 6744 Pav 19h 09m 46s -63° 51' 28" +9,10 17',0x10',7 SABb 21,0 Mly --- --- --- AMMASSI APERTI Sigla Nome Cost. -

The Inner Disk Intermediate-Age Open Cluster NGC 6802⋆
Astronomy & Astrophysics manuscript no. oc6802 c ESO 2017 February 3, 2017 The Gaia-ESO Survey: the inner disk intermediate-age open cluster NGC 6802⋆ B. Tang1, D. Geisler1, E. Friel2, S. Villanova1, R. Smiljanic3, A. R. Casey4, S. Randich5, L. Magrini5, I. San Roman6, C. Muñoz1, 7, R. E. Cohen1, F. Mauro1, A. Bragaglia8, P. Donati8, G. Tautvaišiene˙9, A. Drazdauskas9, R. Ženoviene˙9, O. Snaith10, S. Sousa11, V. Adibekyan11, M. T. Costado12, S. Blanco-Cuaresma13, F. Jiménez-Esteban14, 15, G. Carraro16, T. Zwitter17, P. François18, P. Jofrè4, 19, R. Sordo20, G. Gilmore4, E. Flaccomio21, S. Koposov4, A. J. Korn22, A. C. Lanzafame23, 24, E. Pancino5, 25, A. Bayo26, F. Damiani21, E. Franciosini5, A. Hourihane4, C. Lardo27, J. Lewis4, L. Monaco28, L. Morbidelli5, L. Prisinzano21, G. Sacco5, C. C. Worley4, and S. Zaggia20 1 Departamento de Astronomía, Casilla 160-C, Universidad de Concepción, Concepción, Chile email: [email protected] 2 Department of Astronomy, Indiana University, Bloomington, IN, USA 3 Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716, Warsaw, Poland 4 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK 5 INAF − Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 5, 50125, Florence, Italy 6 Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza San Juan 1, 44001 Teruel, Spain 7 European Southern Observatory, Casilla 19001, Santiago, Chile 8 INAF − Osservatorio Astronomico di Bologna, Via Ranzani, 1, 40127, Bologna, Italy 9 Institute of Theoretical Physics and Astronomy, Vilnius University, Sauletekio av. 3, LT-10222 Vilnius, Lithuania 10 School of Physics, Korea Institute for Advanced Study, 85 Hoegiro, Dongdaemun-gu, Seoul 02455, Republic of Korea 11 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal 12 Instituto de Astrofísica de Andalucía-CSIC, Apdo. -

January 2019 BRAS Newsletter
Monthly Meeting January 14th at 7PM at HRPO (Monthly meetings are on 2nd Mondays, Highland Road Park Observatory). Speaker: Jim Gutierrez, Sunspots, Hot Spots and Relativity What's In This Issue? President’s Message Secretary's Summary Outreach Report Astrophotography Group Comet and Asteroid News Light Pollution Committee Report “Free The Milky Way” Campaign Recent BRAS Forum Entries Messages from the HRPO Science Academy Friday Night Lecture Series Globe at Night Adult Astronomy Courses Total Lunar Eclipse Observing Notes – Ara – The Alter & Mythology Like this newsletter? See PAST ISSUES online back to 2009 Visit us on Facebook – Baton Rouge Astronomical Society Newsletter of the Baton Rouge Astronomical Society January 2019 © 2019 President’s Message First off, I thank you for placing your trust in me for another year. Another thanks goes out to Scott Cadwallader and John R. Nagle for fixing the Library Telescope. The telescope was missing a thumbnut witch Orion Telescope replaced, Scott and John, put the thumbnut back on and reset the collimation. Let’s don’t forget the Total Lunar Eclipse coming up this January 20th. See HRPO announcement below. We are planning 2019 and hope to have an enjoyable year for our members. I’d like to find more opportunity to point our telescopes at the night sky. If there is anything you’d like to see, do, or wish to offer let us know. Our webmaster has set up a private forum: "BRAS Members Only" Group/Section to the "Baton Rouge Astronomical Society Forum" (http://www.brastro.org/phpBB3/). The plan is to use this Group/Section to get additional information to members and get feedback from members without the need of flooding everyone's inbox. -
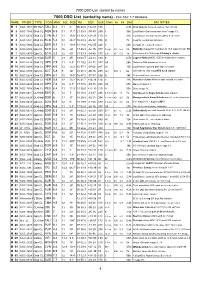
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

Binocular Objects
Southern Skies Binocular list Observing List Evening of 2012 Mar 24 at Karoo Starparty Sunset 18:37, Twilight ends 19:51, Twilight begins 05:13, Sunrise 06:27, Moon rise 08:51, Moon set 19:26 Completely dark from 19:51 to 05:13. New Moon. All times local (GMT+2). Listing All Classes visible above the perfect horizon and in complete darkness after 19:53 and before 05:12. Cls Primary ID Alternate ID Con Mag Size Distance RA 2000 Dec 2000 Begin Optimum End S.A. Ur. 2 PSA Difficulty Optimum EP Glob NGC 6362 Ara 8.1 15.0' 23000 ly 17h31m55.0s -67°02'54" 02:46 05:03 05:25 26 207 60 challenging Open NGC 6208 Collinder 313 Ara 9.5 18.0' 3100 ly 16h49m28.0s -53°43'42" 23:46 04:56 05:35 26 196 58 not visible Glob NGC 6397 Ara 5.3 31.0' 6500 ly 17h40m42.0s -53°40'24" 01:14 05:05 05:32 26 195 58 detectable Open IC 4651 Collinder 327 Ara 8.0 10.0' 2900 ly 17h24m49.0s -49°56'00" 01:30 05:04 05:32 22 181 58 detectable Glob NGC 6352 Ara 7.8 9.0' 64000 ly 17h25m29.0s -48°25'24" 01:35 05:04 05:32 22 181 58 detectable Open Harvard 13 OCL 986 Ara 5.0' 17h03m51.0s -48°05'00" 00:09 05:01 05:38 22 181 58 unknown Open Collinder 227 Melotte 101 Car 8.4 15.0' 6500 ly 10h42m12.0s -65°06'00" 19:51 22:57 02:10 25 210 40 challenging Glob NGC 2808 Car 6.2 14.0' 26000 ly 09h12m03.0s -64°51'48" 19:30 21:27 02:58 25 210 40 detectable Open IC 2602 Collinder 229 Car 1.6 100.0' 520 ly 10h42m58.0s -64°24'00" 19:27 22:58 04:31 25 210 40 obvious Open Collinder 246 Melotte 105 Car 9.4 5.0' 7200 ly 11h19m42.0s -63°29'00" 19:55 23:35 03:17 25 209 40 challenging Open IC 2714 Collinder -

The COLOUR of CREATION Observing and Astrophotography Targets “At a Glance” Guide
The COLOUR of CREATION observing and astrophotography targets “at a glance” guide. (Naked eye, binoculars, small and “monster” scopes) Dear fellow amateur astronomer. Please note - this is a work in progress – compiled from several sources - and undoubtedly WILL contain inaccuracies. It would therefor be HIGHLY appreciated if readers would be so kind as to forward ANY corrections and/ or additions (as the document is still obviously incomplete) to: [email protected]. The document will be updated/ revised/ expanded* on a regular basis, replacing the existing document on the ASSA Pretoria website, as well as on the website: coloursofcreation.co.za . This is by no means intended to be a complete nor an exhaustive listing, but rather an “at a glance guide” (2nd column), that will hopefully assist in choosing or eliminating certain objects in a specific constellation for further research, to determine suitability for observation or astrophotography. There is NO copy right - download at will. Warm regards. JohanM. *Edition 1: June 2016 (“Pre-Karoo Star Party version”). “To me, one of the wonders and lures of astronomy is observing a galaxy… realizing you are detecting ancient photons, emitted by billions of stars, reduced to a magnitude below naked eye detection…lying at a distance beyond comprehension...” ASSA 100. (Auke Slotegraaf). Messier objects. Apparent size: degrees, arc minutes, arc seconds. Interesting info. AKA’s. Emphasis, correction. Coordinates, location. Stars, star groups, etc. Variable stars. Double stars. (Only a small number included. “Colourful Ds. descriptions” taken from the book by Sissy Haas). Carbon star. C Asterisma. (Including many “Streicher” objects, taken from Asterism.