DOCSLIB.ORG

Chapter 2 Meteorology and Oceanography

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 2 Meteorology and Oceanography PART II ACTIONS AND MATERIAL STRENGTH REQUIREMENTS, CHAPTER 2 METROLOGY AND OCEANOGRAPHY Chapter 2 Meteorology and Oceanography 1 Meteorology and Oceanography Items to be Considered for Performance Verification 1.1 General The following meteorology and oceanography items, shall be considered with regard to the performance verification of port facilities. ① Atmospheric pressure and its distribution are factors that generate winds. ② Winds generate waves and storm surge, and affect the wind pressure that acts upon port facilities and moored vessels, and become a factor to interfere with cargo handling and other port operations. See 2 Winds for details. ③ The tidal level affects soil pressure and water pressure, which act on port facilities, and becomes a factor to interfere with cargo handling and other port operations. Also, it has an effect on waves in areas of shallow water. See 3 Tidal level for details. ④ Waves exert wave force on port facilities, and become a factor to interfere with the functioning of port facilities. They also act on moored vessels, causing them to move and interfere with cargo handling and other port operations. They also can raise the mean water level, which has effects similar to the tidal level as mentioned above. See 4 Waves for details. ⑤ Tsunami exerts wave force and fluid force on port facilities, and becomes a factor to interfere with the functioning of port facilities. It also acts on moored ships, causing them to move. See 5 Tsunamis for details. ⑥ Water currents affect sediments on the sea bottom and become a factor to interfere with the functioning of port facilities. See 6 Water Currents etc. for details. – 57 – TECHNICAL STANDARDS AND COMMENTARIES FOR PORT AND HARBOUR FACILITIES IN JAPAN 2 Winds Public Notice Winds Article 6 Characteristics of winds shall be set by the methods provided in the subsequent items corresponding to the single action or combination of two or more actions to be considered in the performance criteria and the performance verification: (1) Ocean surface winds to be used in the estimation of waves and storm surge shall be appropriately defined in terms of wind velocity, wind direction and others based on the long-term wind observation or weather hindcasting. (2) Winds to be used in the calculation of wind pressures shall be appropriately defined in terms of the wind velocity and direction corresponding to the return period through the statistical analysis of the long-term data of observed or hindcasted winds or other methods. (3) Winds to be used in the calculation of wind energy shall be appropriately defined in terms of the joint frequency distribution of wind velocity and direction for a certain duration of time, based on the long- term data of observed or hindcasted winds. [Commentary] 1) Winds to be used in the Estimation of Waves and Storm Surge: Winds to be used in the estimation of waves and storm surge shall be observed or hindcasted values for 30 years or more as a standard. 2) Winds to be used in the Calculation of Wind Pressure: Winds to be used in the calculation of wind pressure shall be observed or hindcasted values for 30 years or more as a standard. [Technical Note] 2.1 General (1) Wind is one of the most distinctive meteorological phenomena, namely, the phenomenon that the air moves due to atmospheric pressure differences and heat. The conditions under which winds blow over the ocean are usually very different than for those over land. Wind velocities over the ocean are much higher than those over land near the shore.1) For performance verification of port facilities, the effects of winds must be appropriately evaluated. (2) Gradient Winds ① The velocity of the gradient wind can be expressed as a function of pressure gradient, radius of curvature of barometic isolines, latitude, and air density as in equation (2.1.1). (2.1.1) where Vg : velocity of gradient wind (m/s); in the case of an anticyclone, equation (2.1.1) gives a negative value and so the absolute value should be taken. ∂p/∂r : pressure gradient (taken to be positive for a cyclone, negative for an anticyclone) (kg/m2/s2) r : radius of curvature of barometic isolines (m) ω : angular velocity of Earth's rotation (1/s) ω =7.27×10-5/s φ : latitude (°) 3 ρa : density of air (kg/m ) Before performing the calculation, measurement units should first be converted into the MKS units listed above. Note that 1º of latitude corresponds to a distance of approximately 1.11 × 105 m, and an air pressure of 1.0 hPa is 100kg/m/s2. – 58 – PART II ACTIONS AND MATERIAL STRENGTH REQUIREMENTS, CHAPTER 2 METROLOGY AND OCEANOGRAPHY ② A gradient wind for which the barometic isolines are straight lines (i.e., their radius of curvature in equation (2.1.1) is infinite) is called the geostrophic wind. In this case, the wind velocity is as equation (2.1.2). (2.1.2) ③ The actual sea surface wind velocity is generally lower than the value obtained from the gradient wind equation. Moreover, although the direction of a gradient wind is parallel to the barometic isolines in theory, the sea surface wind blows at a certain angle α to the barometic isolines in reality as illustrated in Fig. 2.1.2. In the northern hemisphere, the winds around a cyclone blow in a counterclockwise direction and inwards, whereas the winds around an anticyclone blow in a clockwise direction and outwards. It is known that the relationship between the velocity of gradient winds and that of the actual sea surface wind varies with the latitude. This relationship under the average conditions is summarized as in Table 2.1.1.3) α α Low High (a) Cyclone (b) Anticyclone Fig. 2.1.2 Wind Direction for a Cyclone (Low) and an Anticyclone (High) Table 2.1.1 Relationship between Sea Surface Wind Speed and Gradient Wind Speed Latitude (°) 10 20 30 40 50 Angle α (°) 24 20 18 17 15 Velocity ratio Vs /Vg 0.51 0.60 0.64 0.67 0.70 (3) Typhoon Winds In calculations concerning the generation of storm surge or waves due to a typhoon, it is common to assume that the air pressure distribution follows either Fujita’s equation (2.1.3) 4) or Myers’ equation (2.1.4) 4) ; the constants in the chosen equation are determined based on actual air pressure measurements in the region of typhoons. Fujita’s formula (2.1.3) Myers’ formula (2.1.4) where p : air pressure at a distance r from the center of typhoon (hPa) r : distance from the center of typhoon (km) pc : air pressure at the center of typhoon (hPa) r0 : estimated distance from the center of typhoon to the point where the wind velocity is maximum (km) ∆p : air pressure drop at the center of typhoon (hPa) ∆p=p∞-pc p∞ : air pressure at r =∞ (hPa); p∞=pc+∆p The size of a typhoon varies with time, and so r0 and ∆p must be determined as the functions of time (4) Meteorological GPV Organizations such as the Japan Meteorological Agency, the European Center for Medium-Range Weather – 59 – TECHNICAL STANDARDS AND COMMENTARIES FOR PORT AND HARBOUR FACILITIES IN JAPAN Forecasts (ECMWF), and America’s National Center for Environmental Protection (NCEP), calculate the values of items such as air pressure, wind velocity, wind direction, and water vapor flux, based on calculation models for meteorological values that use a three-dimensional calculation grid, and the values at the grid points (GPV: grid point values) are saved. These GPV’s may be used instead of wind hindcastings based on equation (2.1.1) through equation (2.1.4). However, when a grid with large spacing is used for meteorological calculations the atmospheric pressure and winds may not be satisfactorily reproduced at places where meteorological conditions change drastically with position, such as near the centers of typhoons. Therefore, when GPV’s are used, it is preferable to use observational values to verify the precision. (5) Wind Energy If winds are considered as the movement of the air then the wind energy that crosses a unit cross-sectional area in unit time is given by equation (2.1.5).1) Winds for estimating the wind energy shall be appropriately specified with joint statistic distributions for velocity and direction for a fixed time (usually, one year), based on long-term (usually, three years or more) observed or hindcasted data. (2.1.5) where P : wind force energy per unit cross-sectional area (W/m2) 3 ρa : air density (kg/m ) V : wind velocity (m/s) In other words, the wind force energy is proportional to the cube of the wind velocity, so a small difference in wind velocity can mean a big difference in energy (power generation). Therefore, during performance verification of facilities that use wind force energy, it is important to accurately understand how the conditions change with regard to time and space. In the coastal zone the wind conditions varies drastically between land and sea. Also, wind velocity shows great variation on land due to altitude, but over the sea the changes in wind velocity with altitude are gradual, so it is possible to obtain highly stabilized winds that are appropriate for power generation at relatively low altitudes. For example, the results of measurements in the vicinity of the Kansai International Airport, show that the wind energy over the course of a year at a measurement tower (MT station) placed at a height of 15 meters over the ocean were roughly the same as at a land station (C station) with an altitude of 100 meters, and about five times greater than at a land station with an altitude of 10 meters.5) 2.2 Characteristic Values of Wind Velocity (1) Determination of Wind Characteristics The elements of winds are direction and velocity, where the wind direction is expressed as one of sixteen directions and the wind velocity is the mean velocity over 10 minutes.
Load more

Recommended publications
  • A Near-Shore Linear Wave Model with the Mixed Finite Volume and Finite Difference Unstructured Mesh Method
    fluids Article A Near-Shore Linear Wave Model with the Mixed Finite Volume and Finite Difference Unstructured Mesh Method Yong G. Lai 1,* and Han Sang Kim 2 1 Technical Service Center, U.S. Bureau of Reclamation, Denver, CO 80225, USA 2 Bay-Delta Office, California Department of Water Resources, Sacramento, CA 95814, USA; [email protected] * Correspondence: [email protected]; Tel.: +1-303-445-2560 Received: 5 October 2020; Accepted: 1 November 2020; Published: 5 November 2020 Abstract: The near-shore and estuary environment is characterized by complex natural processes. A prominent feature is the wind-generated waves, which transfer energy and lead to various phenomena not observed where the hydrodynamics is dictated only by currents. Over the past several decades, numerical models have been developed to predict the wave and current state and their interactions. Most models, however, have relied on the two-model approach in which the wave model is developed independently of the current model and the two are coupled together through a separate steering module. In this study, a new wave model is developed and embedded in an existing two-dimensional (2D) depth-integrated current model, SRH-2D. The work leads to a new wave–current model based on the one-model approach. The physical processes of the new wave model are based on the latest third-generation formulation in which the spectral wave action balance equation is solved so that the spectrum shape is not pre-imposed and the non-linear effects are not parameterized. New contributions of the present study lie primarily in the numerical method adopted, which include: (a) a new operator-splitting method that allows an implicit solution of the wave action equation in the geographical space; (b) mixed finite volume and finite difference method; (c) unstructured polygonal mesh in the geographical space; and (d) a single mesh for both the wave and current models that paves the way for the use of the one-model approach.
    [Show full text]
  • I. Wind-Driven Coastal Dynamics II. Estuarine Processes
    I. Wind-driven Coastal Dynamics Emily Shroyer, Oregon State University II. Estuarine Processes Andrew Lucas, Scripps Institution of Oceanography Variability in the Ocean Sea Surface Temperature from NASA’s Aqua Satellite (AMSR-E) 10000 km 100 km 1000 km 100 km www.visibleearth.nasa.Gov Variability in the Ocean Sea Surface Temperature (MODIS) <10 km 50 km 500 km Variability in the Ocean Sea Surface Temperature (Field Infrared Imagery) 150 m 150 m ~30 m Relevant spatial scales range many orders of magnitude from ~10000 km to submeter and smaller Plant DischarGe, Ocean ImaginG LanGmuir and Internal Waves, NRL > 1000 yrs ©Dudley Chelton < 1 sec < 1 mm > 10000 km What does a physical oceanographer want to know in order to understand ocean processes? From Merriam-Webster Fluid (noun) : a substance (as a liquid or gas) tending to flow or conform to the outline of its container need to describe both the mass and volume when dealing with fluids Enterà density (ρ) = mass per unit volume = M/V Salinity, Temperature, & Pressure Surface Salinity: Precipitation & Evaporation JPL/NASA Where precipitation exceeds evaporation and river input is low, salinity is increased and vice versa. Note: coastal variations are not evident on this coarse scale map. Surface Temperature- Net warming at low latitudes and cooling at high latitudes. à Need Transport Sea Surface Temperature from NASA’s Aqua Satellite (AMSR-E) www.visibleearth.nasa.Gov Perpetual Ocean hWp://svs.Gsfc.nasa.Gov/cGi-bin/details.cGi?aid=3827 Es_manG the Circulaon and Climate of the Ocean- Dimitris Menemenlis What happens when the wind blows on Coastal Circulaon the surface of the ocean??? 1.
    [Show full text]
  • Wind-Induced Waves and Currents in a Nearshore Zone
    CHAPTER 260 Wind-Induced Waves and Currents in a Nearshore Zone Nobuhiro Matsunaga1, Misao Hashida2 and Hiroshi Kawakami3 Abstract Characteristics of waves and currents induced when a strong wind blows shoreward in a nearshore zone have been investigated experimentally. The drag coefficient of wavy surface has been related to the ratio u*a/cP, where u*a is the air friction velocity on the water surface and cP the phase velocity of the predominant wind waves. Though the relation between the frequencies of the predominant waves and fetch is very similar to that for deep water, the fetch-relation of the wave energy is a little complicated because of the wave shoaling and the wave breaking. The dependence of the energy spectra on the frequency /changes from /-5 to/"3 in the high frequency region with increase of the wind velocity. A strong onshore drift current forms along a thin layer near the water surface and the compensating offshore current is induced under this layer. As the wind velocity increases, the offshore current velocity increases and becomes much larger than the wave-induced mass transport velocity which is calculated from Longuet- Higgins' theoretical solution. 1. Introduction When a nearshore zone is under swell weather conditions, the 1 Associate Professor, Department of Earth System Science and Technology, Kyushu University, Kasuga 816, Japan. 2 Professor, Department of Civil Engineering, Nippon Bunri University, Oita 870-03, Japan. 3 Graduate student, Department of Earth System Science and Technology, Kyushu University, Kasuga 816, Japan. 3363 3364 COASTAL ENGINEERING 1996 wind Fig.l Sketch of sediment transport process in a nearshore zone under a storm.
    [Show full text]
  • 1D Laboratory Study on Wave-Induced Setup Over A
    1 LES Modeling of Tsunami-like Solitary Wave Processes 2 over Fringing Reefs 3 4 Yu Yao1, 4, Tiancheng He1, Zhengzhi Deng2*, Long Chen1, 3, Huiqun Guo1 5 6 1 School of Hydraulic Engineering, Changsha University of Science and Technology, 7 Changsha, Hunan 410114, China. 8 2 Ocean College, Zhejiang University, Zhoushan, Zhejiang 316021, China. 9 3 Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of 10 Hunan Province, Changsha 410114, China. 11 4Key Laboratory of Coastal Disasters and Defence of Ministry of Education, 12 Nanjing, Jiangsu 210098, China 13 14 15 16 * Corresponding author: Zhengzhi Deng 17 E-mail: [email protected] 18 Tel: +86 15068188376 19 1 20 ABSTRACT 21 Many low-lying tropical and sub-tropical reef-fringed coasts are vulnerable to 22 inundation during tsunami events. Hence accurate prediction of tsunami wave 23 transformation and runup over such reefs is a primary concern in the coastal management 24 of hazard mitigation. To overcome the deficiencies of using depth-integrated models in 25 modeling tsunami-like solitary waves interacting with fringing reefs, a three-dimensional 26 (3D) numerical wave tank based on the Computational Fluid Dynamics (CFD) tool 27 OpenFOAM® is developed in this study. The Navier-Stokes equations for two-phase 28 incompressible flow are solved, using the Large Eddy Simulation (LES) method for 29 turbulence closure and the Volume of Fluid (VOF) method for tracking the free surface. 30 The adopted model is firstly validated by two existing laboratory experiments with 31 various wave conditions and reef configurations. The model is then applied to examine 32 the impacts of varying reef morphologies (fore-reef slope, back-reef slope, lagoon width, 33 reef-crest width) on the solitary wave runup.
    [Show full text]
  • 1DH Boussinesq Modeling of Wave Transformation Over Fringing Reefs
    Ocean Engineering 47 (2012) 30–42 Contents lists available at SciVerse ScienceDirect Ocean Engineering journal homepage: www.elsevier.com/locate/oceaneng 1DH Boussinesq modeling of wave transformation over fringing reefs Yu Yao a, Zhenhua Huang a,b,n, Stephen G. Monismith c, Edmond Y.M. Lo a a School of Civil and Environmental Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore b Earth Observatory of Singapore (EOS), Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore c Department of Civil and Environmental Engineering, Stanford University, 473 Via Ortega, Stanford, CA 94305-4020, USA article info abstract Article history: To better understand wave transformation process and the associated hydrodynamic characteristics Received 14 May 2011 over fringing coral reefs, we present a numerical study, which is based on one-dimensional (1D) fully Accepted 12 March 2012 nonlinear Boussinesq equations, of the wave-induced setups/setdowns and wave height changes over Editor-in-Chief: A.I. Incecik various fringing reef profiles. An empirical eddy viscosity model is adopted to account for wave breaking and a shock-capturing finite volume (FV)-based solver is employed to ensure the computa- Keywords: tional accuracy and stability for steep reef faces and shallow reef flats. The numerical results are Wave-induced setup compared with a series of published laboratory experiments. Our results show that with an appropriate Wave-induced setdown treatment of boundary conditions and a fine-tuned eddy viscosity model, the full nonlinear Boussinesq Boussinesq equations model can give satisfactory predictions of the wave height as well as the mean water level over various Coral reef hydrodynamics reef profiles with different reef-flat submergences and reef-crest configurations under both mono- Mean water level Wave breaking chromatic and spectral waves.
    [Show full text]
  • Waves and Sediment Transport in the Nearshore Zone - R.G.D
    COASTAL ZONES AND ESTUARIES – Waves and Sediment Transport in the Nearshore Zone - R.G.D. Davidson-Arnott, B. Greenwood WAVES AND SEDIMENT TRANSPORT IN THE NEARSHORE ZONE R.G.D. Davidson-Arnott Department of Geography, University of Guelph, Canada B. Greenwood Department of Geography, University of Toronto, Canada Keywords: wave shoaling, wave breaking, surf zone, currents, sediment transport Contents 1. Introduction 2. Definition of the nearshore zone 3. Wave shoaling 4. The surf zone 4.1. Wave breaking 4.2. Surf zone circulation 5. Sediment transport 5.1. Shore-normal transport 5.2. Longshore transport 6. Conclusions Glossary Bibliography Biographical Sketches Summary The nearshore zone extends from the low tide line out to a water depth where wave motion ceases to affect the sea floor. As waves travel from the outer limits of the nearshore zone towards the shore they are increasingly affected by the bed through the process of wave shoaling and eventually wave breaking. In turn, as water depth decreases wave motion and sediment transport at the bed increases. In addition to the orbital motion associated with the waves, wave breaking generates strong unidirectional currents UNESCOwithin the surf zone close to the – beach EOLSS and this is responsible for the transport of sediment both on-offshore and alongshore. SAMPLE CHAPTERS 1. Introduction The nearshore zone extends from the limit of the beach exposed at low tides seaward to a water depth at which wave action during storms ceases to appreciably affect the bottom. On steeply sloping coasts the nearshore zone may be less than 100 m wide and on some gently sloping coasts it may extend offshore for more than 5 km - however, on many coasts the nearshore zone is 0.5-2.5 km in width and extends into water depths >40m.
    [Show full text]
  • Developing Wave Energy in Coastal California
    Arnold Schwarzenegger Governor DEVELOPING WAVE ENERGY IN COASTAL CALIFORNIA: POTENTIAL SOCIO-ECONOMIC AND ENVIRONMENTAL EFFECTS Prepared For: California Energy Commission Public Interest Energy Research Program REPORT PIER FINAL PROJECT and California Ocean Protection Council November 2008 CEC-500-2008-083 Prepared By: H. T. Harvey & Associates, Project Manager: Peter A. Nelson California Energy Commission Contract No. 500-07-036 California Ocean Protection Grant No: 07-107 Prepared For California Ocean Protection Council California Energy Commission Laura Engeman Melinda Dorin & Joe O’Hagan Contract Manager Contract Manager Christine Blackburn Linda Spiegel Deputy Program Manager Program Area Lead Energy-Related Environmental Research Neal Fishman Ocean Program Manager Mike Gravely Office Manager Drew Bohan Energy Systems Research Office Executive Policy Officer Martha Krebs, Ph.D. Sam Schuchat PIER Director Executive Officer; Council Secretary Thom Kelly, Ph.D. Deputy Director ENERGY RESEARCH & DEVELOPMENT DIVISION Melissa Jones Executive Director DISCLAIMER This report was prepared as the result of work sponsored by the California Energy Commission. It does not necessarily represent the views of the Energy Commission, its employees or the State of California. The Energy Commission, the State of California, its employees, contractors and subcontractors make no warrant, express or implied, and assume no legal liability for the information in this report; nor does any party represent that the uses of this information will not infringe upon privately owned rights. This report has not been approved or disapproved by the California Energy Commission nor has the California Energy Commission passed upon the accuracy or adequacy of the information in this report. Acknowledgements The authors acknowledge the able leadership and graceful persistence of Laura Engeman at the California Ocean Protection Council.
    [Show full text]
  • Wave Transformation Wave Transformation
    FFEMAOCUSED INTERNAL STUDY R REPORTEVIEWS NOT FOR DISTRIBUTION WaveWave Transformation Transformation FEMA Coastal Flood Hazard Analysis FEMAand Mapping Coastal Guidelines Flood Hazard Analysis Focused and Mapping Study ReportGuidelines February May 2005 2004 Focused Study Leader Focused Study Leader Bob Battalio, P.E. Bob Battalio, P.E. Team Members Team Members Carmela Chandrasekera, Ph.D. Carmela Chandrasekera,David Divoky Ph.D. Darryl Hatheway,David Divoky, CFM P.E. DarrylTerry Hatheway, Hull, P.E. CFM Bill O’Reilly,Terry Hull, Ph.D. P.E. Dick Seymour,Bill O’Reilly, Ph.D., P.E. Ph.D. RajeshDick Srinivas, Seymour, Ph.D., Ph.D., P.E. P.E. Rajesh Srinivas, Ph.D., P.E. FOCUSED STUDY REPORTS WAVE TRANSFORMATION Table of Contents 1 INTRODUCTION....................................................................................................................... 1 1.1 Category and Topics ..................................................................................................... 1 1.2 Wave Transformation Focused Study Group ............................................................... 1 1.3 General Description of Wave Transformation Processes and Pertinence to Coastal Flood Studies ................................................................................................... 1 2 CRITICAL TOPICS ................................................................................................................. 16 2.1 Topic 8: Wave Transformations With and Without Regional Models....................... 16 2.1.1 Description of
    [Show full text]
  • Numerical Simulation of Sea Surface Directional Wave Spectra Under Hurricane Wind Forcing Il-Ju Moon University of Rhode Island
    University of Rhode Island DigitalCommons@URI Graduate School of Oceanography Faculty Graduate School of Oceanography Publications 2003 Numerical Simulation of Sea Surface Directional Wave Spectra under Hurricane Wind Forcing Il-Ju Moon University of Rhode Island Isaac Ginis University of Rhode Island, [email protected] See next page for additional authors Follow this and additional works at: https://digitalcommons.uri.edu/gsofacpubs Citation/Publisher Attribution Moon, I.-J., Ginis, I., Hara, T., Tolman, H. L., Wright, C. W., & Walsh, E. J. (2003). Numerical Simulation of Sea Surface Directional Wave Spectra under Hurricane Wind Forcing. Journal of Physical Oceanography, 33, 1680-1706. doi: 10.1175/ 1520-0485(2003)0332.0.CO;2 Available at: http://dx.doi.org/10.1175/1520-0485(2003)033<1680:NSOSSD>2.0.CO;2 This Article is brought to you for free and open access by the Graduate School of Oceanography at DigitalCommons@URI. It has been accepted for inclusion in Graduate School of Oceanography Faculty Publications by an authorized administrator of DigitalCommons@URI. For more information, please contact [email protected]. Authors Il-Ju Moon, Isaac Ginis, Tetsu Hara, Hendrik L. Tolman, C. W. Wright, and Edward J. Walsh This article is available at DigitalCommons@URI: https://digitalcommons.uri.edu/gsofacpubs/360 1680 JOURNAL OF PHYSICAL OCEANOGRAPHY VOLUME 33 Numerical Simulation of Sea Surface Directional Wave Spectra under Hurricane Wind Forcing IL-JU MOON,ISAAC GINIS, AND TETSU HARA Graduate School of Oceanography, University of Rhode Island, Narragansett, Rhode Island HENDRIK L. TOLMAN SAIC-GSO at NOAA/NCEP Environmental Modeling Center, Camp Springs, Maryland C.
    [Show full text]
  • Chapter 8 Coasts
    CHAPTER 8 COASTS 1. INTRODUCTION 1.1 The term coastal studies, which is in common use for a great variety of approaches to coastlines, covers a large area of endeavor. What do I mean by the term coastal? There are various definitions or interpretations, depending on how much or how little is included seaward and landward of the shoreline. The shoreline is fairly generally taken to be the line or trace where the sea meets the land, and this is fairly well defined except in areas with estuaries, tidal flats, etc., unless you want to quibble about where the high-water line is. 1.2 In this course I’m going to interpret the term coast in a fairly broad sense to mean a marine area extending from the shoreline out onto the continental shelf for some distance, together with some land area immediately landward of the shoreline. This admittedly sloppy definition succeeds in generally including areas both seaward and landward of the shoreline in which a great variety of processes operate that most people would categorize as coastal processes. I intend the definition to include only the innermost part of the continental shelf, the part that’s most strongly affected by the adjacent shoreline. (The continental shelf is the broad belt of shallow water adjacent to the coastline. In many areas of the world it is as much as a few hundred kilometers wide, and water depths at the shelf edge are no more than about two hundred meters.) In many coastal areas there’s a well defined coastal plain that may be well over a hundred kilometers wide; only the part nearest the shoreline, directly affected by modern coastal processes, is included in my definition.
    [Show full text]
  • A New Model of Shoaling and Breaking Waves: One-Dimensional Solitary Wave on a Mild Sloping Beach Maria Kazakova, Gaël Loïc Richard
    A new model of shoaling and breaking waves: One-dimensional solitary wave on a mild sloping beach Maria Kazakova, Gaël Loïc Richard To cite this version: Maria Kazakova, Gaël Loïc Richard. A new model of shoaling and breaking waves: One-dimensional solitary wave on a mild sloping beach. 2018. hal-01824889 HAL Id: hal-01824889 https://hal.archives-ouvertes.fr/hal-01824889 Preprint submitted on 27 Jun 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A new model of shoaling and breaking waves: One-dimensional solitary wave on a mild sloping beach M. Kazakova1 and G. L. Richard∗,2 1Intitut de Math´ematiques de Toulouse, UMR5219, Universit´ede Toulouse, CNRS, UPS, F-31062 Toulouse Cedex 9, France 2LAMA, UMR5127, Universit´eSavoie Mont Blanc, CNRS, 73376 Le Bourget-du-Lac, France Abstract We present a new approach to model coastal waves in the shoaling and surf zones. The model can be described as a depth-averaged large-eddy simulation model with a cutoff in the inertial subrange. The large-scale turbulence is explicitly resolved through an extra variable called enstrophy while the small-scale turbulence is modelled with a turbulent viscosity hypothesis.
    [Show full text]
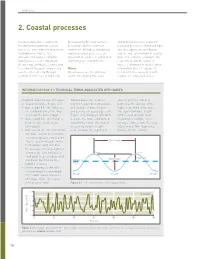
  • 2. Coastal Processes
    CHAPTER 2 2. Coastal processes Coastal landscapes result from by weakening the rock surface and driving nearshore sediment the interaction between coastal to facilitate further sediment transport processes. Wind and tides processes and sediment movement. movement. Biological, biophysical are also significant contributors, Hydrodynamic (waves, tides and biochemical processes are and are indeed dominant in coastal and currents) and aerodynamic important in coral reef, salt marsh dune and estuarine environments, (wind) processes are important. and mangrove environments. respectively, but the action of Weathering contributes significantly waves is dominant in most settings. to sediment transport along rocky Waves Information Box 2.1 explains the coasts, either directly through Ocean waves are the principal technical terms associated with solution of minerals, or indirectly agents for shaping the coast regular (or sinusoidal) waves. INFORMATION BOX 2.1 TECHNICAL TERMS ASSOCIATED WITH WAVES Important characteristics of regular, Natural waves are, however, wave height (Hs), which is or sinusoidal, waves (Figure 2.1). highly irregular (not sinusoidal), defined as the average of the • wave height (H) – the difference and a range of wave heights highest one-third of the waves. in elevation between the wave and periods are usually present The significant wave height crest and the wave trough (Figure 2.2), making it difficult to off the coast of south-west • wave length (L) – the distance describe the wave conditions in England, for example, is, on between successive crests quantitative terms. One way of average, 1.5m, despite the area (or troughs) measuring variable height experiencing 10m-high waves • wave period (T) – the time from is to calculate the significant during extreme storms.
    [Show full text]