DOCSLIB.ORG

1DH Boussinesq Modeling of Wave Transformation Over Fringing Reefs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1DH Boussinesq Modeling of Wave Transformation Over Fringing Reefs Ocean Engineering 47 (2012) 30–42 Contents lists available at SciVerse ScienceDirect Ocean Engineering journal homepage: www.elsevier.com/locate/oceaneng 1DH Boussinesq modeling of wave transformation over fringing reefs Yu Yao a, Zhenhua Huang a,b,n, Stephen G. Monismith c, Edmond Y.M. Lo a a School of Civil and Environmental Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore b Earth Observatory of Singapore (EOS), Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore c Department of Civil and Environmental Engineering, Stanford University, 473 Via Ortega, Stanford, CA 94305-4020, USA article info abstract Article history: To better understand wave transformation process and the associated hydrodynamic characteristics Received 14 May 2011 over fringing coral reefs, we present a numerical study, which is based on one-dimensional (1D) fully Accepted 12 March 2012 nonlinear Boussinesq equations, of the wave-induced setups/setdowns and wave height changes over Editor-in-Chief: A.I. Incecik various fringing reef profiles. An empirical eddy viscosity model is adopted to account for wave breaking and a shock-capturing finite volume (FV)-based solver is employed to ensure the computa- Keywords: tional accuracy and stability for steep reef faces and shallow reef flats. The numerical results are Wave-induced setup compared with a series of published laboratory experiments. Our results show that with an appropriate Wave-induced setdown treatment of boundary conditions and a fine-tuned eddy viscosity model, the full nonlinear Boussinesq Boussinesq equations model can give satisfactory predictions of the wave height as well as the mean water level over various Coral reef hydrodynamics reef profiles with different reef-flat submergences and reef-crest configurations under both mono- Mean water level Wave breaking chromatic and spectral waves. The primary 1D wave transformation processes, including nonlinear shoaling, refection, breaking, generation of higher harmonics and infragravity waves, can also be reasonably captured. Finally, the model is applied to study the effects of reef-face slopes and profile shapes on the distribution of the wave height and mean water level over the fringing reefs. & 2012 Elsevier Ltd. All rights reserved. 1. Introduction almost-constant wave-induced setup over the reef top where the water is shallow and the depth is nearly constant. The low- Wave interaction with fringing coral reefs has been a primary frequency motions due to the so-called surf beat or reef-flat focus of nearshore hydrodynamics over decades. The physics of resonance might exist on the reef flat as well (e.g., Pe´quignet waves on reefs are different from that of waves on normal coastal et al., 2009). Since fringing reefs shelter many tropical islands beaches in many respects, including the roughness of the sub- from the flood hazards associated with tsunamis, hurricanes, and strate and the variety of geometries. A typical fringing reef is high surf events (Roeber et al., 2010), the wave-induced setup and characterized by a seaward sloping reef face and an inshore wave-generated currents across reef flats may have profound shallow reef flat extending towards the coastline. Corals com- geological, ecological, engineering and environmental implica- monly grow to mean low tide levels and may impose a shallow tions (see Gourlay and Colleter, 2005). water control on the waves reaching reef flats. Similar to the wave Precise characteristics of wave dynamics and the energy transformation over a shallow shelf, ocean waves first shoal on a dissipation through wave breaking are controlled mainly by the fore-reef face and then break either on the reef face or on the reef morphology of reef profile (reef-flat water depth, reef-face slope, flat. As a result, a shoaling-induced setdown can be observed and reef-flat width) and incident wave conditions. Although the before the breaking point, accompanying a breaking-induced reef profile may vary from site to site, ridges or similar config- setup after the breaking point. The surfzone always extends over urations (‘‘reef rim’’ or ‘‘reef crest’’ in some papers) have been a certain distance on the reef flat, starting from the incipient frequently observed at the edges of coral reefs (Gourlay, 1996b; breaking point to the location where the wave breaking ceases. Jago et al., 2007; Hench et al., 2008). Ridges, consisting of coral After wave breaking, very short waves may reform on the reef colonies, rubble algal, etc., function like bars or submerged flat and propagate towards the shoreline, accompanying an breakwaters to filter a substantial portion of the incident wave energy; their effect on wave-induced setup has been investigated experimentally by Yao et al. (2009) using an idealized rectangular n Corresponding author at: School of Civil and Environmental Engineering, Nanyang ridge model. Technological University, 50 Nanyang Avenue, Singapore 639651, Singapore. Tel.: þ65 67904737. Hydrodynamics associated with waves on fringing coral reefs E-mail address: [email protected] (Z. Huang). is more complex than that on plane beaches: a typical fringing 0029-8018/$ - see front matter & 2012 Elsevier Ltd. All rights reserved. http://dx.doi.org/10.1016/j.oceaneng.2012.03.010 Y. Yao et al. / Ocean Engineering 47 (2012) 30–42 31 coral reef involves a transition of bottom profile from deep to waves transforming over a reef profile that is similar to the one shallow waters over a long distance, as well as a porous reef used by Skotner and Apelt (1999), they confirmed the ability of surface which may provide high resistance to the waves above. their Boussinesq model in describing the variation of significant Numerical modeling of nearshore coral reef hydrodynamics faces wave height, the mean water level across the reef profile, the several challenges such as the steep reef-face slopes (e.g., Seelig, evolution of the wave spectrum, the generation of infragravity 1983; Gourlay, 1996a; Vetter et al., 2010), the complex config- oscillations and shoreline runups. More recently, Roeber et al. urations of reef crest and flat (e.g., Seelig, 1983; Hench et al., (2010) employed a shock-capturing Boussinesq-type model to 2008), the spatially-varied roughness of reef surface (e.g., Lowe simulate the solitary wave transformation over fringing reefs, et al., 2005). Also, the wave transformation usually needs to be which involved energetic wave breaking, bore propagation and modeled at a long time scale (several hundred waves) and a large the transition from subcritical to supercritical flows under an space scale (over the entire reef profile). initially dry reef crest. Over decades, analytical models frequently deal with the one- The main objective of this study is to implement and validate a dimensional horizontal (1DH) idealized reef profiles (a typical weakly dispersive and fully nonlinear depth-integrated Boussi- idealized reef profile has a plane sloping reef face and a horizontal nesq-type model1 to help interpret some of our previous labora- platform reef flat). Conventionally, in analogy to the wave-driven tory work (Yao et al., 2009) and other similar published work on alongshore flows and the wave-induced setup/setdown on bea- wave transformation over fringing reefs. The following three ches (e.g., Svendsen, 2006), analytical solutions based on the reasons made us to adopt the fully nonlinear Boussinesq equa- radiation stress concept introduced by Longuet-Higgins and tions in this study: (1) Skotner and Apelt (1999) speculated that Stewart (1964) had been used frequently in the past to study the use of weakly nonlinear equations might improve the predic- 1DH reef hydrodynamics (Gourlay, 1996a; Symonds et al., 1995; tion of wave-induced setdown and setup; (2) the presence of a Hearn, 1999; Gourlay and Colleter, 2005). In recent years, the ridge at the edge of the reef would cause the waves to be highly effects of complex bathymetry and different forcing mechanisms nonlinear in its vicinity; (3) the present fully nonlinear Boussi- have been modeled by using two-dimensional horizontal (2DH) nesq model is capable of simulating a wide range of long and and three-dimensional (3D) models to study both the waves and short wave problems (Lynett et al., 2002; Hsiao et al., 2005; the mean flows, and usually the radiation stress concept is used to Lynett, 2006), and the model has also been applied to wave couple the waves and the mean flows (Kraines et al., 1998, 1999; overtopping over a levee system by Lynett et al. (2010). Yao et al. Douillet et al., 2001; Luick et al., 2007). The modeling results (2011) reported a preliminary validation of the present model for presented by Lowe et al. (2009) look very promising, even though an idealized reef profile. This study will first report comprehen- the predicted the mean water level was not as accurate as the sive comparisons between the numerical simulations and the computed wave heights and currents. Compared to field studies, available published data for various wave conditions and different fewer numerical models have been applied to well-controlled, fringing reef configurations. The effects of the reef face shapes and small-scale laboratory investigations in the literature. sloping angles on the mean water levels and wave heights will The most advanced Navier–Stokes approaches, e.g., the RANS- also be investigated using the validated numerical model. based models (Lin and Liu, 1998; Losada et al., 2005; Lara et al., The remaining of this paper is organized as follows. In Section 2, 2008; Torres-Freyermuth et al., 2010), are well suited for simulat- the mathematical formulation, numerical scheme, boundary condi- ing breaking waves and wave-structure interactions in small tions and energy dissipation sub-model are described. In Section 3, confined regions. However, Navier–Stokes approaches are still numerical simulations are compared with available experimental very computationally expensive to run, especially for the near- data for four representative scenarios to show the robustness of the shore zones where a large number of grid points and a fine mesh model.
Load more

Recommended publications
  • A Near-Shore Linear Wave Model with the Mixed Finite Volume and Finite Difference Unstructured Mesh Method
    fluids Article A Near-Shore Linear Wave Model with the Mixed Finite Volume and Finite Difference Unstructured Mesh Method Yong G. Lai 1,* and Han Sang Kim 2 1 Technical Service Center, U.S. Bureau of Reclamation, Denver, CO 80225, USA 2 Bay-Delta Office, California Department of Water Resources, Sacramento, CA 95814, USA; [email protected] * Correspondence: [email protected]; Tel.: +1-303-445-2560 Received: 5 October 2020; Accepted: 1 November 2020; Published: 5 November 2020 Abstract: The near-shore and estuary environment is characterized by complex natural processes. A prominent feature is the wind-generated waves, which transfer energy and lead to various phenomena not observed where the hydrodynamics is dictated only by currents. Over the past several decades, numerical models have been developed to predict the wave and current state and their interactions. Most models, however, have relied on the two-model approach in which the wave model is developed independently of the current model and the two are coupled together through a separate steering module. In this study, a new wave model is developed and embedded in an existing two-dimensional (2D) depth-integrated current model, SRH-2D. The work leads to a new wave–current model based on the one-model approach. The physical processes of the new wave model are based on the latest third-generation formulation in which the spectral wave action balance equation is solved so that the spectrum shape is not pre-imposed and the non-linear effects are not parameterized. New contributions of the present study lie primarily in the numerical method adopted, which include: (a) a new operator-splitting method that allows an implicit solution of the wave action equation in the geographical space; (b) mixed finite volume and finite difference method; (c) unstructured polygonal mesh in the geographical space; and (d) a single mesh for both the wave and current models that paves the way for the use of the one-model approach.
    [Show full text]
  • I. Wind-Driven Coastal Dynamics II. Estuarine Processes
    I. Wind-driven Coastal Dynamics Emily Shroyer, Oregon State University II. Estuarine Processes Andrew Lucas, Scripps Institution of Oceanography Variability in the Ocean Sea Surface Temperature from NASA’s Aqua Satellite (AMSR-E) 10000 km 100 km 1000 km 100 km www.visibleearth.nasa.Gov Variability in the Ocean Sea Surface Temperature (MODIS) <10 km 50 km 500 km Variability in the Ocean Sea Surface Temperature (Field Infrared Imagery) 150 m 150 m ~30 m Relevant spatial scales range many orders of magnitude from ~10000 km to submeter and smaller Plant DischarGe, Ocean ImaginG LanGmuir and Internal Waves, NRL > 1000 yrs ©Dudley Chelton < 1 sec < 1 mm > 10000 km What does a physical oceanographer want to know in order to understand ocean processes? From Merriam-Webster Fluid (noun) : a substance (as a liquid or gas) tending to flow or conform to the outline of its container need to describe both the mass and volume when dealing with fluids Enterà density (ρ) = mass per unit volume = M/V Salinity, Temperature, & Pressure Surface Salinity: Precipitation & Evaporation JPL/NASA Where precipitation exceeds evaporation and river input is low, salinity is increased and vice versa. Note: coastal variations are not evident on this coarse scale map. Surface Temperature- Net warming at low latitudes and cooling at high latitudes. à Need Transport Sea Surface Temperature from NASA’s Aqua Satellite (AMSR-E) www.visibleearth.nasa.Gov Perpetual Ocean hWp://svs.Gsfc.nasa.Gov/cGi-bin/details.cGi?aid=3827 Es_manG the Circulaon and Climate of the Ocean- Dimitris Menemenlis What happens when the wind blows on Coastal Circulaon the surface of the ocean??? 1.
    [Show full text]
  • Wind-Induced Waves and Currents in a Nearshore Zone
    CHAPTER 260 Wind-Induced Waves and Currents in a Nearshore Zone Nobuhiro Matsunaga1, Misao Hashida2 and Hiroshi Kawakami3 Abstract Characteristics of waves and currents induced when a strong wind blows shoreward in a nearshore zone have been investigated experimentally. The drag coefficient of wavy surface has been related to the ratio u*a/cP, where u*a is the air friction velocity on the water surface and cP the phase velocity of the predominant wind waves. Though the relation between the frequencies of the predominant waves and fetch is very similar to that for deep water, the fetch-relation of the wave energy is a little complicated because of the wave shoaling and the wave breaking. The dependence of the energy spectra on the frequency /changes from /-5 to/"3 in the high frequency region with increase of the wind velocity. A strong onshore drift current forms along a thin layer near the water surface and the compensating offshore current is induced under this layer. As the wind velocity increases, the offshore current velocity increases and becomes much larger than the wave-induced mass transport velocity which is calculated from Longuet- Higgins' theoretical solution. 1. Introduction When a nearshore zone is under swell weather conditions, the 1 Associate Professor, Department of Earth System Science and Technology, Kyushu University, Kasuga 816, Japan. 2 Professor, Department of Civil Engineering, Nippon Bunri University, Oita 870-03, Japan. 3 Graduate student, Department of Earth System Science and Technology, Kyushu University, Kasuga 816, Japan. 3363 3364 COASTAL ENGINEERING 1996 wind Fig.l Sketch of sediment transport process in a nearshore zone under a storm.
    [Show full text]
  • 1D Laboratory Study on Wave-Induced Setup Over A
    1 LES Modeling of Tsunami-like Solitary Wave Processes 2 over Fringing Reefs 3 4 Yu Yao1, 4, Tiancheng He1, Zhengzhi Deng2*, Long Chen1, 3, Huiqun Guo1 5 6 1 School of Hydraulic Engineering, Changsha University of Science and Technology, 7 Changsha, Hunan 410114, China. 8 2 Ocean College, Zhejiang University, Zhoushan, Zhejiang 316021, China. 9 3 Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of 10 Hunan Province, Changsha 410114, China. 11 4Key Laboratory of Coastal Disasters and Defence of Ministry of Education, 12 Nanjing, Jiangsu 210098, China 13 14 15 16 * Corresponding author: Zhengzhi Deng 17 E-mail: [email protected] 18 Tel: +86 15068188376 19 1 20 ABSTRACT 21 Many low-lying tropical and sub-tropical reef-fringed coasts are vulnerable to 22 inundation during tsunami events. Hence accurate prediction of tsunami wave 23 transformation and runup over such reefs is a primary concern in the coastal management 24 of hazard mitigation. To overcome the deficiencies of using depth-integrated models in 25 modeling tsunami-like solitary waves interacting with fringing reefs, a three-dimensional 26 (3D) numerical wave tank based on the Computational Fluid Dynamics (CFD) tool 27 OpenFOAM® is developed in this study. The Navier-Stokes equations for two-phase 28 incompressible flow are solved, using the Large Eddy Simulation (LES) method for 29 turbulence closure and the Volume of Fluid (VOF) method for tracking the free surface. 30 The adopted model is firstly validated by two existing laboratory experiments with 31 various wave conditions and reef configurations. The model is then applied to examine 32 the impacts of varying reef morphologies (fore-reef slope, back-reef slope, lagoon width, 33 reef-crest width) on the solitary wave runup.
    [Show full text]
  • Waves and Sediment Transport in the Nearshore Zone - R.G.D
    COASTAL ZONES AND ESTUARIES – Waves and Sediment Transport in the Nearshore Zone - R.G.D. Davidson-Arnott, B. Greenwood WAVES AND SEDIMENT TRANSPORT IN THE NEARSHORE ZONE R.G.D. Davidson-Arnott Department of Geography, University of Guelph, Canada B. Greenwood Department of Geography, University of Toronto, Canada Keywords: wave shoaling, wave breaking, surf zone, currents, sediment transport Contents 1. Introduction 2. Definition of the nearshore zone 3. Wave shoaling 4. The surf zone 4.1. Wave breaking 4.2. Surf zone circulation 5. Sediment transport 5.1. Shore-normal transport 5.2. Longshore transport 6. Conclusions Glossary Bibliography Biographical Sketches Summary The nearshore zone extends from the low tide line out to a water depth where wave motion ceases to affect the sea floor. As waves travel from the outer limits of the nearshore zone towards the shore they are increasingly affected by the bed through the process of wave shoaling and eventually wave breaking. In turn, as water depth decreases wave motion and sediment transport at the bed increases. In addition to the orbital motion associated with the waves, wave breaking generates strong unidirectional currents UNESCOwithin the surf zone close to the – beach EOLSS and this is responsible for the transport of sediment both on-offshore and alongshore. SAMPLE CHAPTERS 1. Introduction The nearshore zone extends from the limit of the beach exposed at low tides seaward to a water depth at which wave action during storms ceases to appreciably affect the bottom. On steeply sloping coasts the nearshore zone may be less than 100 m wide and on some gently sloping coasts it may extend offshore for more than 5 km - however, on many coasts the nearshore zone is 0.5-2.5 km in width and extends into water depths >40m.
    [Show full text]
  • Developing Wave Energy in Coastal California
    Arnold Schwarzenegger Governor DEVELOPING WAVE ENERGY IN COASTAL CALIFORNIA: POTENTIAL SOCIO-ECONOMIC AND ENVIRONMENTAL EFFECTS Prepared For: California Energy Commission Public Interest Energy Research Program REPORT PIER FINAL PROJECT and California Ocean Protection Council November 2008 CEC-500-2008-083 Prepared By: H. T. Harvey & Associates, Project Manager: Peter A. Nelson California Energy Commission Contract No. 500-07-036 California Ocean Protection Grant No: 07-107 Prepared For California Ocean Protection Council California Energy Commission Laura Engeman Melinda Dorin & Joe O’Hagan Contract Manager Contract Manager Christine Blackburn Linda Spiegel Deputy Program Manager Program Area Lead Energy-Related Environmental Research Neal Fishman Ocean Program Manager Mike Gravely Office Manager Drew Bohan Energy Systems Research Office Executive Policy Officer Martha Krebs, Ph.D. Sam Schuchat PIER Director Executive Officer; Council Secretary Thom Kelly, Ph.D. Deputy Director ENERGY RESEARCH & DEVELOPMENT DIVISION Melissa Jones Executive Director DISCLAIMER This report was prepared as the result of work sponsored by the California Energy Commission. It does not necessarily represent the views of the Energy Commission, its employees or the State of California. The Energy Commission, the State of California, its employees, contractors and subcontractors make no warrant, express or implied, and assume no legal liability for the information in this report; nor does any party represent that the uses of this information will not infringe upon privately owned rights. This report has not been approved or disapproved by the California Energy Commission nor has the California Energy Commission passed upon the accuracy or adequacy of the information in this report. Acknowledgements The authors acknowledge the able leadership and graceful persistence of Laura Engeman at the California Ocean Protection Council.
    [Show full text]
  • Wave Transformation Wave Transformation
    FFEMAOCUSED INTERNAL STUDY R REPORTEVIEWS NOT FOR DISTRIBUTION WaveWave Transformation Transformation FEMA Coastal Flood Hazard Analysis FEMAand Mapping Coastal Guidelines Flood Hazard Analysis Focused and Mapping Study ReportGuidelines February May 2005 2004 Focused Study Leader Focused Study Leader Bob Battalio, P.E. Bob Battalio, P.E. Team Members Team Members Carmela Chandrasekera, Ph.D. Carmela Chandrasekera,David Divoky Ph.D. Darryl Hatheway,David Divoky, CFM P.E. DarrylTerry Hatheway, Hull, P.E. CFM Bill O’Reilly,Terry Hull, Ph.D. P.E. Dick Seymour,Bill O’Reilly, Ph.D., P.E. Ph.D. RajeshDick Srinivas, Seymour, Ph.D., Ph.D., P.E. P.E. Rajesh Srinivas, Ph.D., P.E. FOCUSED STUDY REPORTS WAVE TRANSFORMATION Table of Contents 1 INTRODUCTION....................................................................................................................... 1 1.1 Category and Topics ..................................................................................................... 1 1.2 Wave Transformation Focused Study Group ............................................................... 1 1.3 General Description of Wave Transformation Processes and Pertinence to Coastal Flood Studies ................................................................................................... 1 2 CRITICAL TOPICS ................................................................................................................. 16 2.1 Topic 8: Wave Transformations With and Without Regional Models....................... 16 2.1.1 Description of
    [Show full text]
  • Numerical Simulation of Sea Surface Directional Wave Spectra Under Hurricane Wind Forcing Il-Ju Moon University of Rhode Island
    University of Rhode Island DigitalCommons@URI Graduate School of Oceanography Faculty Graduate School of Oceanography Publications 2003 Numerical Simulation of Sea Surface Directional Wave Spectra under Hurricane Wind Forcing Il-Ju Moon University of Rhode Island Isaac Ginis University of Rhode Island, [email protected] See next page for additional authors Follow this and additional works at: https://digitalcommons.uri.edu/gsofacpubs Citation/Publisher Attribution Moon, I.-J., Ginis, I., Hara, T., Tolman, H. L., Wright, C. W., & Walsh, E. J. (2003). Numerical Simulation of Sea Surface Directional Wave Spectra under Hurricane Wind Forcing. Journal of Physical Oceanography, 33, 1680-1706. doi: 10.1175/ 1520-0485(2003)0332.0.CO;2 Available at: http://dx.doi.org/10.1175/1520-0485(2003)033<1680:NSOSSD>2.0.CO;2 This Article is brought to you for free and open access by the Graduate School of Oceanography at DigitalCommons@URI. It has been accepted for inclusion in Graduate School of Oceanography Faculty Publications by an authorized administrator of DigitalCommons@URI. For more information, please contact [email protected]. Authors Il-Ju Moon, Isaac Ginis, Tetsu Hara, Hendrik L. Tolman, C. W. Wright, and Edward J. Walsh This article is available at DigitalCommons@URI: https://digitalcommons.uri.edu/gsofacpubs/360 1680 JOURNAL OF PHYSICAL OCEANOGRAPHY VOLUME 33 Numerical Simulation of Sea Surface Directional Wave Spectra under Hurricane Wind Forcing IL-JU MOON,ISAAC GINIS, AND TETSU HARA Graduate School of Oceanography, University of Rhode Island, Narragansett, Rhode Island HENDRIK L. TOLMAN SAIC-GSO at NOAA/NCEP Environmental Modeling Center, Camp Springs, Maryland C.
    [Show full text]
  • Chapter 8 Coasts
    CHAPTER 8 COASTS 1. INTRODUCTION 1.1 The term coastal studies, which is in common use for a great variety of approaches to coastlines, covers a large area of endeavor. What do I mean by the term coastal? There are various definitions or interpretations, depending on how much or how little is included seaward and landward of the shoreline. The shoreline is fairly generally taken to be the line or trace where the sea meets the land, and this is fairly well defined except in areas with estuaries, tidal flats, etc., unless you want to quibble about where the high-water line is. 1.2 In this course I’m going to interpret the term coast in a fairly broad sense to mean a marine area extending from the shoreline out onto the continental shelf for some distance, together with some land area immediately landward of the shoreline. This admittedly sloppy definition succeeds in generally including areas both seaward and landward of the shoreline in which a great variety of processes operate that most people would categorize as coastal processes. I intend the definition to include only the innermost part of the continental shelf, the part that’s most strongly affected by the adjacent shoreline. (The continental shelf is the broad belt of shallow water adjacent to the coastline. In many areas of the world it is as much as a few hundred kilometers wide, and water depths at the shelf edge are no more than about two hundred meters.) In many coastal areas there’s a well defined coastal plain that may be well over a hundred kilometers wide; only the part nearest the shoreline, directly affected by modern coastal processes, is included in my definition.
    [Show full text]
  • A New Model of Shoaling and Breaking Waves: One-Dimensional Solitary Wave on a Mild Sloping Beach Maria Kazakova, Gaël Loïc Richard
    A new model of shoaling and breaking waves: One-dimensional solitary wave on a mild sloping beach Maria Kazakova, Gaël Loïc Richard To cite this version: Maria Kazakova, Gaël Loïc Richard. A new model of shoaling and breaking waves: One-dimensional solitary wave on a mild sloping beach. 2018. hal-01824889 HAL Id: hal-01824889 https://hal.archives-ouvertes.fr/hal-01824889 Preprint submitted on 27 Jun 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A new model of shoaling and breaking waves: One-dimensional solitary wave on a mild sloping beach M. Kazakova1 and G. L. Richard∗,2 1Intitut de Math´ematiques de Toulouse, UMR5219, Universit´ede Toulouse, CNRS, UPS, F-31062 Toulouse Cedex 9, France 2LAMA, UMR5127, Universit´eSavoie Mont Blanc, CNRS, 73376 Le Bourget-du-Lac, France Abstract We present a new approach to model coastal waves in the shoaling and surf zones. The model can be described as a depth-averaged large-eddy simulation model with a cutoff in the inertial subrange. The large-scale turbulence is explicitly resolved through an extra variable called enstrophy while the small-scale turbulence is modelled with a turbulent viscosity hypothesis.
    [Show full text]
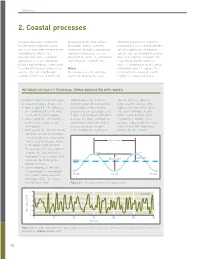
  • 2. Coastal Processes
    CHAPTER 2 2. Coastal processes Coastal landscapes result from by weakening the rock surface and driving nearshore sediment the interaction between coastal to facilitate further sediment transport processes. Wind and tides processes and sediment movement. movement. Biological, biophysical are also significant contributors, Hydrodynamic (waves, tides and biochemical processes are and are indeed dominant in coastal and currents) and aerodynamic important in coral reef, salt marsh dune and estuarine environments, (wind) processes are important. and mangrove environments. respectively, but the action of Weathering contributes significantly waves is dominant in most settings. to sediment transport along rocky Waves Information Box 2.1 explains the coasts, either directly through Ocean waves are the principal technical terms associated with solution of minerals, or indirectly agents for shaping the coast regular (or sinusoidal) waves. INFORMATION BOX 2.1 TECHNICAL TERMS ASSOCIATED WITH WAVES Important characteristics of regular, Natural waves are, however, wave height (Hs), which is or sinusoidal, waves (Figure 2.1). highly irregular (not sinusoidal), defined as the average of the • wave height (H) – the difference and a range of wave heights highest one-third of the waves. in elevation between the wave and periods are usually present The significant wave height crest and the wave trough (Figure 2.2), making it difficult to off the coast of south-west • wave length (L) – the distance describe the wave conditions in England, for example, is, on between successive crests quantitative terms. One way of average, 1.5m, despite the area (or troughs) measuring variable height experiencing 10m-high waves • wave period (T) – the time from is to calculate the significant during extreme storms.
    [Show full text]
  • Experimental Study on the Influence of an Artificial Reef on Cross-Shore
    water Article Experimental Study on the Influence of an Artificial Reef on Cross-Shore Morphodynamic Processes of a Wave-Dominated Beach Yue Ma 1 , Cuiping Kuang 1,*, Xuejian Han 1, Haibo Niu 2, Yuhua Zheng 1 and Chao Shen 1 1 College of Civil Engineering, Tongji University, Shanghai 200092, China; [email protected] (Y.M.); [email protected] (X.H.); [email protected] (Y.Z.); [email protected] (C.S.) 2 Department of Engineering, Dalhousie University, Truro, NS B2N 5E3, Canada; [email protected] * Correspondence: [email protected] Received: 4 August 2020; Accepted: 18 October 2020; Published: 21 October 2020 Abstract: Artificial reefs are being implemented around the world for their multi-functions including coastal protection and environmental improvement. To better understand the hydrodynamic and morphodynamic roles of an artificial reef (AR) in beach protection, a series of experiments were conducted in a 50 m-long wave flume configured with a 1:10 sloping beach and a model AR (1.8 m long 0.3 m high) with 0.2 m submergence depth. Five regular and five irregular wave × conditions were generated on two types of beach profiles (with/without model AR) to study the cross-shore hydrodynamic and morphological evolution process. The influences of AR on the processes are concluded as follows: (1) AR significantly decreases the incident wave energy, and its dissipation effect differs for higher and lower harmonics under irregular wave climates; (2) AR changes the cross-shore patterns of hydrodynamic factors (significant wave height,
    [Show full text]